Influence of a Magnetic Guide Field on Injection in Wakefield Acceleration ()
1. Introduction
In the LWFA process, an electron density bubble [1,2] is driven in low density plasma by the laser pulse through the ponder motive force. For intensities high enough, self injection of electrons into the wake can take place, and a charge can be accelerated. It is well known that trapping of the background electrons begins much below the longitudinal wave-breaking limit [3-5]. The transverse wavebreaking regime is the situation where a static magnetic field should play an important role.
A theoretical model for electron self-injection, in the case when a strong magnetic field is applied, is reported in this paper. The spatial distribution of the potential created by the bubble is calculated. It is shown that the magnetic field reduces the transverse motion of electrons, making trapping in the accelerating bubble more likely. It is also shown, with PIC code simulations, in good agreement with results previously published [5], that the electric charge accelerated can be enhanced by a static magnetic field.
2. Theoretical Model
In this theoretical approach, the bubble is assumed to be a sphere moving in plasma along the z-axis with relativistic velocity 
[6]. Dimensionless units are used. The time is normalized to
, the length to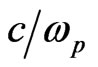
, the velocity to c, the electric field to
, the magnetic field to
, and the electron density to the background density n0. The variable 
is introduced. In the laboratory frame, the following convenient gauge is used: 
[6-9]. Inside the bubble one can consider that 
as the intensity of the laser pulse has a nonzero value only very close to the front of the cavity. Then one has to solve the following two equations: 
and 
[6,7]. Considering that one has a cylindrical symmetry, the solution is
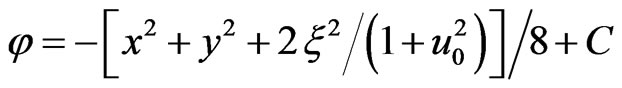
where C is a constant. The electron sheath around the cavity screens the ion field in the surrounding plasma. The radial electrostatic field acting on a relativistic electron is modelled as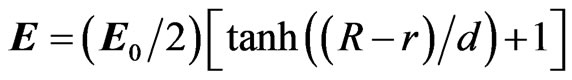 
where R is the sphere radius, d is the width of the electron sheath, r is given by 
where 
is defined by:
. Vector 
reads: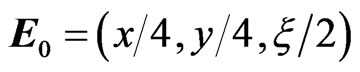
. Taking into account this screening function leads to the following scalar potential [6,8,9]
(1)
where:
. The constant of integration was chosen such as 
when r goes to infinity. It was shown numerically that 
varies slowly close to the center of the bubble and decreases very rapidly close to the electron sheath.
The Hamiltonian of one electron is:
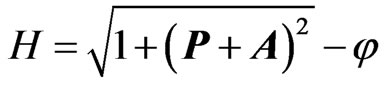where 
is the canonical momentum of the electron. Then, the canonical transformation:
, given by the type-2 generating function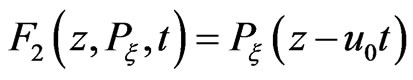 
is performed. The new canonical variables are defined by 
and
, the new Hamiltonian, in terms of the new variables, reads 
. Some electrons which are not trapped in the wakefield are trapped when a very high magnitude static magnetic field is applied (Figure 1).
Many trajectories are bent by the magnetic field, keeping particles closer to the rear of the bubble. Then, the electron trapping is more likely to occur.
The equation for variable 
is given by:
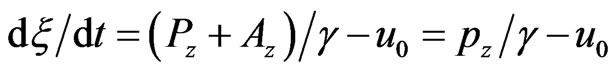. At a point of return in the cavity, the following condition must be satisfied:
(a)
(b)
Figure 1. One electron trajectory with and without the magnetic static field. R = 10, d = 0.5, pz0 = 0.5, px0 = 0. (a) B0 = 0; (b) B0 = 1.
(a)
(b)
Figure 2. Electron density in the first bubble. a = 5, n = 3.4 × 1017 cm−3. (a) B0 = 0; (b) B0 = 120 T.
Figure 3. Electron energy distribution in the first bubble. a = 5, n = 3.4 × 1017 cm−3. (a) B0 = 0; (b) B0 = 120 T.
. Assuming that particles have an initial Hamiltonian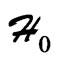
, the domain in phase space where electrons are trapped can be defined by [6]
(2)
As this condition [Equation (2)], and the potential inside the bubble are the same as those previously obtained by Kostyukov et al. ignoring the magnetic field, the trapping condition, 
, is still valid [6,8,9]. As we only consider very high intensity lasers interacting with low density plasma, u0 will not be significantly affected by a static magnetic field. Moreover, the size of the bubble is not significantly modified by the static magnetic field in the situations considered in our PIC code simulations. Consequently, the enhancement of electron trapping, in the PIC code simulation results described in the next paragraph, seems to be mainly due to the fact that strong static magnetic fields will partly suppress the transverse motion of electrons.
3. PIC Code Simulation Results
Numerical simulations were conducted using the twodimensional PIC code CALDER [10]. As shown in Figures 2 and 3, a static magnetic field applied in parallel with the direction of propagation of the driving laser pulse does enhance the particle trapping in the first bubble.
4. Conclusion
The influence of a strong static magnetic field parallel to the direction of propagation of the laser pulse on electron trapping in the accelerating electron cavity has been studied. The trapping condition is formally the same as the one previously derived by Kostyukov et al. [6]. The enhanced trapping associated to the magnetic field is due to the fact that trajectories are bent which suppresses partially the particles’ transverse motion. Numerical simulations were also conducted, they confirm that a constant magnetic field is an important controlling knob for improving the electron trapping in the LWFA process.