1. Introduction
We derive an explicit expression for the pure vector superfield in gauge theories in the Wess-Zumino gauge from which the supersymmetric action is directly obtained from a so-called  -term. By a pure vector superfield, it is meant that its theta independent part transforms as a Lorentz vector. The pure vector superfield is not to be confused with the well known (scalar)-vector superfield [1-4] obtained by imposing a reality condition on the general scalar superfield, whose theta independent part is a scalar, and neither is to be confused with the well known spinor superfield [1-4], whose theta independent part is a spinor, both containing a vector field, and the supersymmetric action is obtained from the latter from a so-called
-term. By a pure vector superfield, it is meant that its theta independent part transforms as a Lorentz vector. The pure vector superfield is not to be confused with the well known (scalar)-vector superfield [1-4] obtained by imposing a reality condition on the general scalar superfield, whose theta independent part is a scalar, and neither is to be confused with the well known spinor superfield [1-4], whose theta independent part is a spinor, both containing a vector field, and the supersymmetric action is obtained from the latter from a so-called  -term. Although the derivation is somehow tedious, the theta dependent part of the pure vector superfield turns out to be not complicated.
-term. Although the derivation is somehow tedious, the theta dependent part of the pure vector superfield turns out to be not complicated.
2. The Pure Vector Superfield: Its Explicit Expression
In the celebrated Wess-Zumino gauge, and in a four component representation, the (scalar)-vector superfield takes the form [5,6]
 (1)
(1)
with the following residual gauge transformation
 (2)
(2)
where the gauge function  is given by
is given by
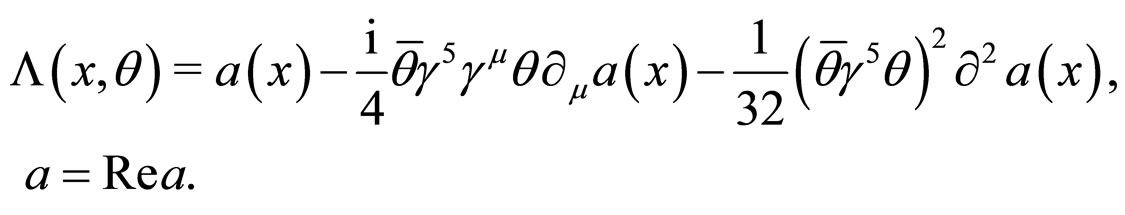 (3)
(3)
One may define a pure vector superfield [5,6] as follows
 (4)
(4)
where  is the charge conjugation matrix in the chiral representation. Under the supergauge transformation Equation (2),
is the charge conjugation matrix in the chiral representation. Under the supergauge transformation Equation (2),
 (5)
(5)
where we recall that  is left-chiral and hence
is left-chiral and hence  is right-chiral. Accordingly, they are, respectively, annihilated by the supercovariant derivatives
is right-chiral. Accordingly, they are, respectively, annihilated by the supercovariant derivatives
 where
where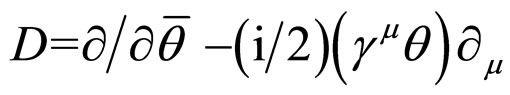 . That is,
. That is,
 (6)
(6)
We may rewrite the transformation rule in Equation (5) as
 (7)
(7)
Due to the first equality in Equation (6), we may replace the product  in the second term on the extreme right-hand side of Equation (7) by their anticommutator. This anti-commutator may be obtained from
in the second term on the extreme right-hand side of Equation (7) by their anticommutator. This anti-commutator may be obtained from  by multiplying it by
by multiplying it by

leading to
 (8)
(8)
and showing that it transforms as a non-abelian gauge field.
Using the relations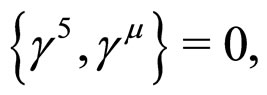 ,
, 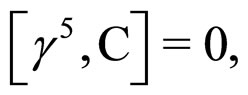
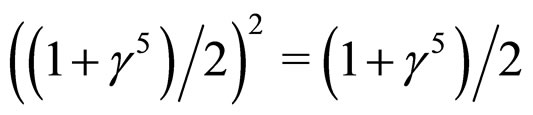
Equation (4) may be equivalently re-expressed as
 (9)
(9)
In the Wess-Zumino gauge,
 (10)
(10)
Applying the supercovariant derivative  to it and using, in the process, the expansion of the product
to it and using, in the process, the expansion of the product  together with the orthogonality relations between the product of any of two of
together with the orthogonality relations between the product of any of two of ,
,  ,
,  , give
, give
 (11)
(11)
Multiplying the latter equation by
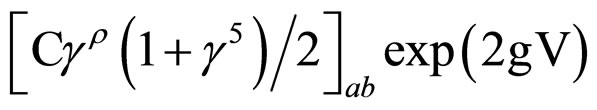
from the left, leads to
 (12)
(12)
Now we apply 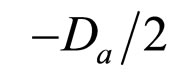 to the above equation, and use, in the process, the following properties,
to the above equation, and use, in the process, the following properties,
 (13)
(13)
to obtain
 (14)
(14)
where
 (15)
(15)
 (16)
(16)
 (17)
(17)
The identities
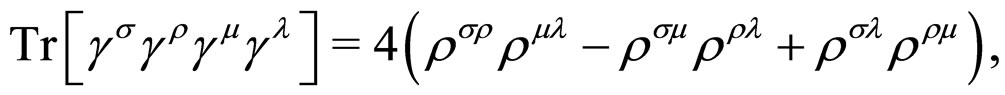
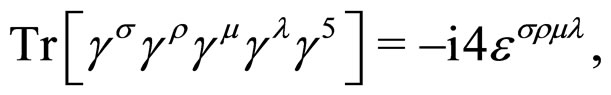 (18)
(18)
and , lead to the following expressions for
, lead to the following expressions for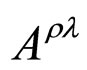 , and
, and ,
,
 (19)
(19)
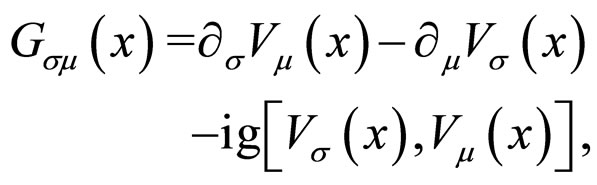 (20)
(20)
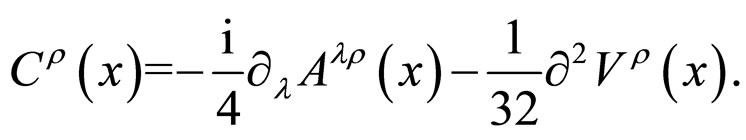 (21)
(21)
Before giving the final expression for , we note it may be now re-written as
, we note it may be now re-written as
 (22)
(22)
since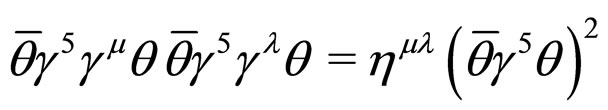 , hence
, hence
 (23)
(23)
as is easily checked, where note that the quadratic term  from the exponential generates also a term
from the exponential generates also a term  from the
from the  -independent term
-independent term  within the square brackets in Equation (23). Since the exponential term represents the translation operator of the argument
within the square brackets in Equation (23). Since the exponential term represents the translation operator of the argument  of the component fields by
of the component fields by , our final expression for
, our final expression for , in the Wess-Zumino supergauge, becomes simply
, in the Wess-Zumino supergauge, becomes simply
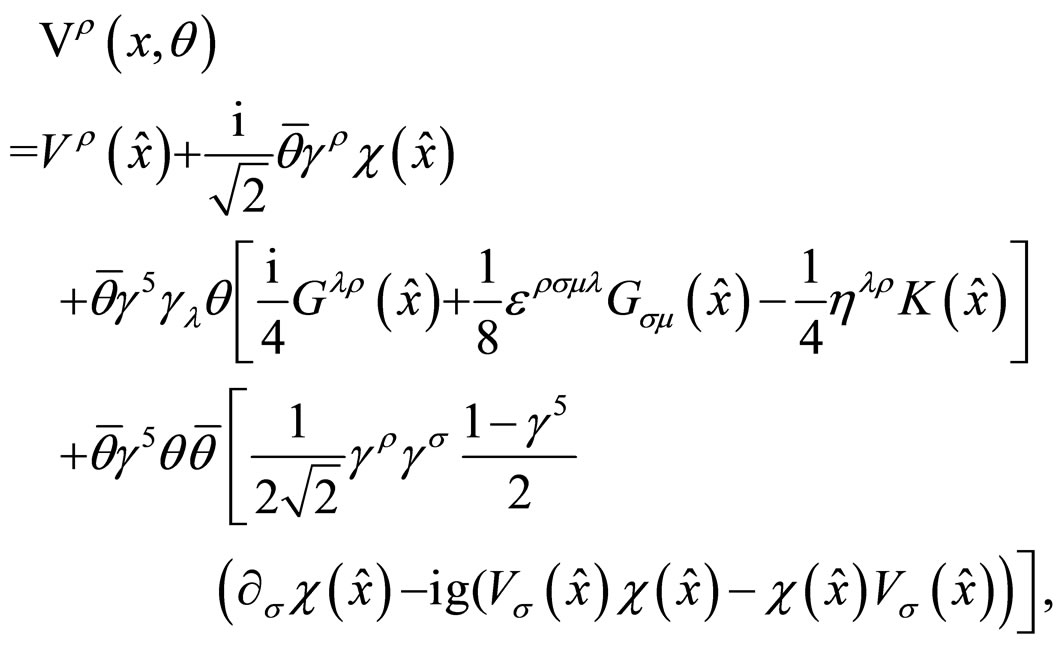 (24)
(24)
 (25)
(25)
Using the relation , with the (Hermitian) matrices
, with the (Hermitian) matrices  as the generators of the underlying group, Equation (24) is equivalently expressed as
as the generators of the underlying group, Equation (24) is equivalently expressed as
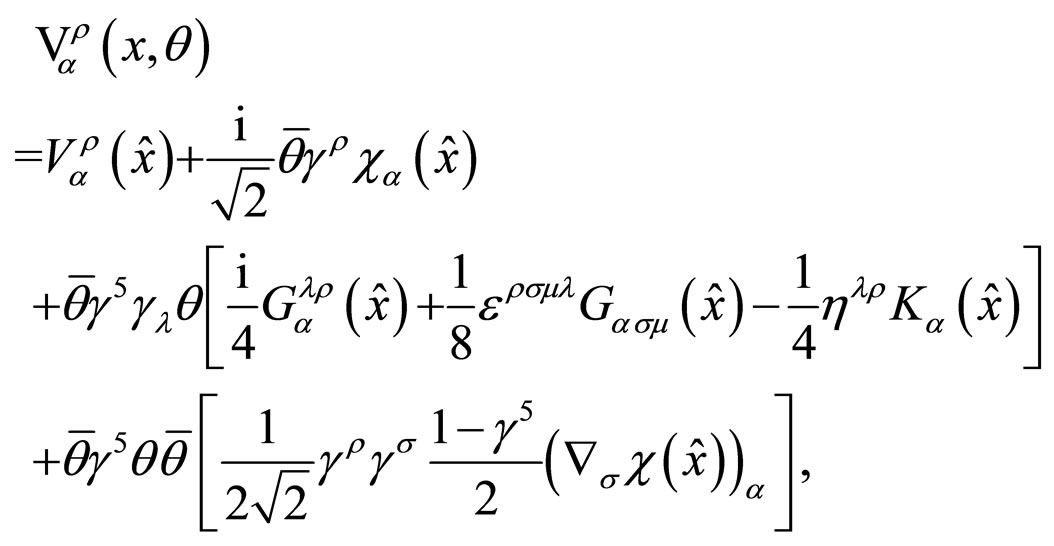 (26)
(26)
where
 (27)
(27)
 (28)
(28)
and  denotes the adjoint representation of the generators.
denotes the adjoint representation of the generators.
3. Conclusion
Although the derivation is somehow tedious, the final expression of the pure vector superfield and its theta dependent part are not complicated. The explicit expression for the pure vector superfield allows the construction of the supersymmetric action corresponding directly to the so-called  -term, as is readily checked, rather than from the
-term, as is readily checked, rather than from the 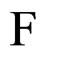 -term constructed out of a spinor superfield, as is usually done. We hope that this novel expression of a pure vector superfield, derived here, will be useful in supersymmetric (vector) gauge theories and justifies this analysis.
-term constructed out of a spinor superfield, as is usually done. We hope that this novel expression of a pure vector superfield, derived here, will be useful in supersymmetric (vector) gauge theories and justifies this analysis.
4. Acknowledgements
The author would like to thank his colleagues at the Institute for the interest they have shown in this work.