A Note on the Statistical Approximation Properties of the Modified Discrete Operators ()
1. Introduction
First of all, let us recall the concept of statistical convergence. The natural density (or density) of the set  is denoted as
is denoted as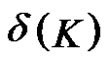 .
.
For 
whenever the limit exists (see e.g. [1]) if for every
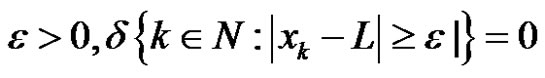
then we say that a sequence  is said to be statistcally convergent to a number of L (see Fast in [2]).
is said to be statistcally convergent to a number of L (see Fast in [2]).
The concept of statistical convergence is very important in approximation theory because although any sequence which is convergent in ordinary sense is statistically convergent, but contrary can not be true all the time. For instance;
If we choose  as
as
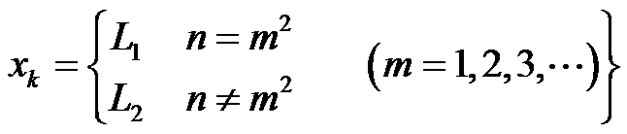
then we can easily say that it is statistically convergent to  but not convergent in ordinary sense when
but not convergent in ordinary sense when .Recently, linear positive operators and their Korovkin type statistical approximation properties have been investigated by many authors. It is well-known that lots of operators were defined with infinite series. Details can be found in [3]. For example, n-th Favard-Mirakjan-Szász operator was defined by
.Recently, linear positive operators and their Korovkin type statistical approximation properties have been investigated by many authors. It is well-known that lots of operators were defined with infinite series. Details can be found in [3]. For example, n-th Favard-Mirakjan-Szász operator was defined by
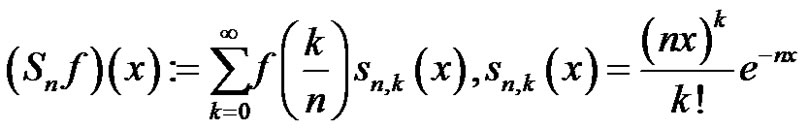
for every f belonging to Banach lattice ,
,  and
and  where
where
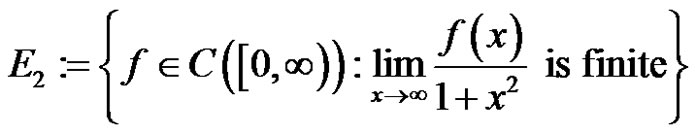
is endowed with the norm .
.
In [4], Doğru investigate the weighted approximation properties of general positive linear operators on infinite intervals. Later, in 2002, weighted approximation properties of Szász-type operators are investigated by same author in [5]. In this note, we investigate the statistical approximation properties considering only the partial sums of the operators. In [6], J. Grof studied on the operator
 (1)
(1)
where 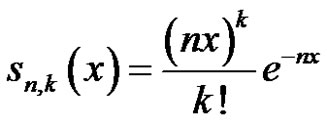 and he verified that if
and he verified that if  is a sequence of positive integers such that
is a sequence of positive integers such that
 then
then  for all
for all
 and
and  Here, f satisfies the inequality
Here, f satisfies the inequality
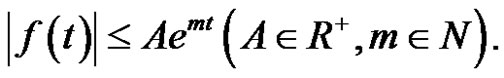
In 1984, Heintz-Gerd Lehnhoff [7] studied the following Modified Szász operators
 (2)
(2)
where ,
, 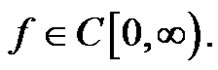
Grof and Lehnhoff obtained the conditions which ensure the convergence of the operators  to f.
to f.
Notice that the notation  shows the largest integer and it is not exceeding the number
shows the largest integer and it is not exceeding the number .
.
The main aim of this paper is to investigate the statistical approximation properties of the operators which constructed and examined the ordinary approximation properties by Agratini in [8].
2. Statistical Approximation Properties
Let us recall the operators which were defined by Agratini in [8].
Throughout the paper , K indicates a compact subinterval of
, K indicates a compact subinterval of  and
and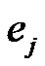 , the j-th monomial,
, the j-th monomial, 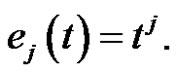
Let us assume that the following cases for each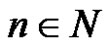
1) For every , a sequence of
, a sequence of  exists such that
exists such that
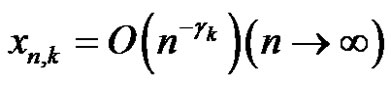
a net on  is fixed.
is fixed.
2) There is a sequence  such that
such that
 . Where,
. Where,  is the space of all realvalued functions continuously differentiable in IR+.
is the space of all realvalued functions continuously differentiable in IR+.
For this sequence  the following conditions
the following conditions
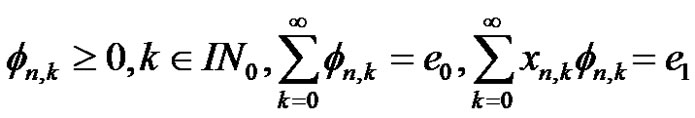 (3)
(3)
hold.
3) A positive function 
 , exists with the property,
, exists with the property,
 (4)
(4)
By using these requirements the operators were defined as
 (5)
(5)
where F stands for the domain of  containing the set of all continuous functions on
containing the set of all continuous functions on 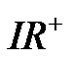 for which the series in (5) is convergent.
for which the series in (5) is convergent.
We note that, with specific choosing these operators turn into the operators mentioned in [1].
Lemma A. [8] Let ,
,  , be defined by (5) and
, be defined by (5) and 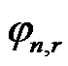 be the r-th central moment of
be the r-th central moment of . For every
. For every  , we have the following identities,
, we have the following identities,
 (6)
(6)
 (7)
(7)
 (8)
(8)
A Korovkin type statistical approximation theorem for any sequence of positive linear operators was proved by Gadjiev and Orhan in [9]. First, let us recall this theorem.
Where  denotes all functions f that are continuous in [a,b] and bounded all positive axis.
denotes all functions f that are continuous in [a,b] and bounded all positive axis.
Theorem A. [9] If the sequence of positive linear operators  satisfies the conditions
satisfies the conditions
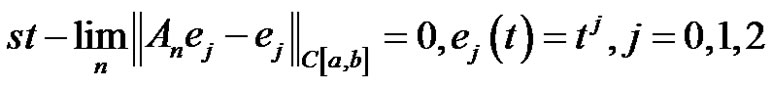
then for any function  we have,
we have,

Now, we can give the following theorem which includes the satatistical convergence of the operators in (5).
Theorem 1. Let , be the operators defined in (5). If
, be the operators defined in (5). If  uniformly on K then for every
uniformly on K then for every 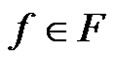 we have,
we have,
 (9)
(9)
Proof. Because of (3) we can easily say that
 (10)
(10)
and
 (11)
(11)
We know from (8) that
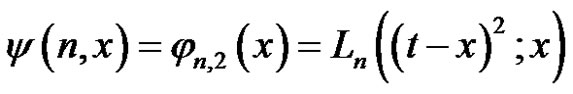 . By using the linearity of the operator
. By using the linearity of the operator
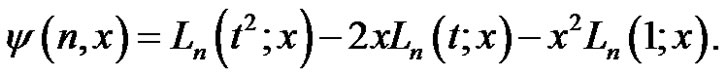
From (3)
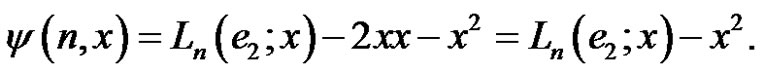
Hence,
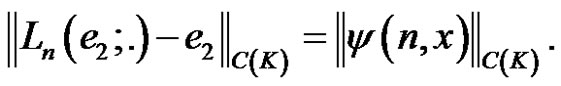
In view of 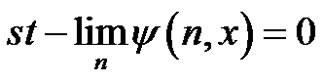 we have
we have
 (12)
(12)
Now, we are able to say in the light of Theorem A that
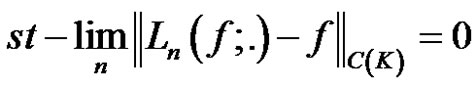 which ends the proof.
which ends the proof.
By using modulus of continuity, we mention about the rate of statistical convergence of these operators. First, let us remember the definition of modulus of continuity. Let  the modulus of continuity of f, is defined as
the modulus of continuity of f, is defined as
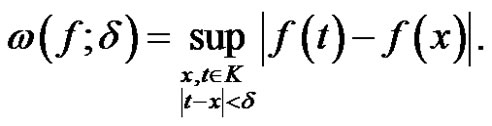
Let  be defined by (5), for every
be defined by (5), for every 
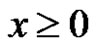 and
and 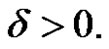 We know from Theorem 1 in [8] that
We know from Theorem 1 in [8] that
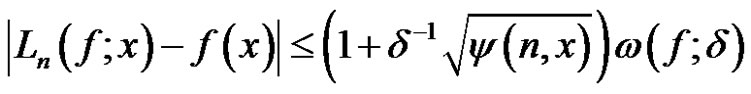 (13)
(13)
If we take norm on K and choose , we get
, we get  Due to
Due to
 , we have the rates of statistical convergence of the operators in (5).
, we have the rates of statistical convergence of the operators in (5).
3. Modified Discrete Operators
In this section, we recall the modified discrete operators which were defined by Agratini in [8] and investigate the statistical approximation properties of these operators. If we specialize the net  and function
and function  respectively,
respectively,
 (14)
(14)
under these assumptions, the requirement of Theorem 1 is fulfilled. Starting from (5) under the additional assumptions (14) Agratini defined,
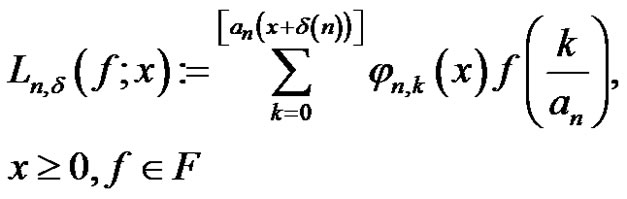 (15)
(15)
where,  is a sequence of positive numbers.
is a sequence of positive numbers.
The study of these operators were developed in polynomial weighted spaces connected to the weights
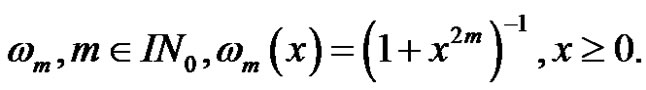 For every
For every 
 the spaces
the spaces
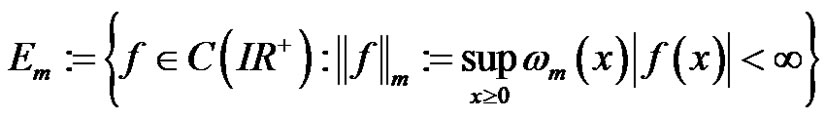
endowed with the norm 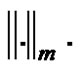
Lemma B. [8] Let  be defined by (5) and the assumptions (14) are fulfilled. If,
be defined by (5) and the assumptions (14) are fulfilled. If, 
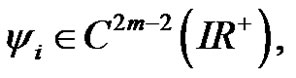 then the central moment of 2m-th order verifies
then the central moment of 2m-th order verifies
 (16)
(16)
Where 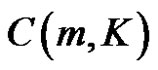 is a constant depending only on m and the compact K.
is a constant depending only on m and the compact K.
Theorem 2. Let  be defined by (15). If
be defined by (15). If

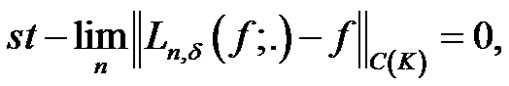
holds for every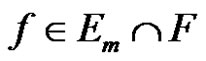 .
.
Proof. We use the following,
 (17)
(17)
and for  which are the positive constants
which are the positive constants  hold true. Hence,
hold true. Hence,

From this inequality,
 (18)
(18)
If  then
then  On the grounds of
On the grounds of 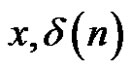 and
and  are positive we can write that
are positive we can write that
 (19)
(19)
The remaining term is  and taking into consideration both (18) and (19)
and taking into consideration both (18) and (19)

By using (16)

If we take norm on K we have the following.
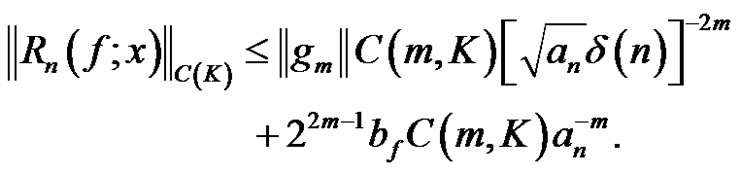
By considering the concept of statistical convergence let us define the sets,
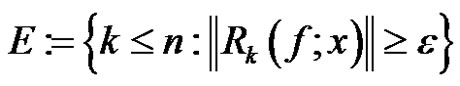
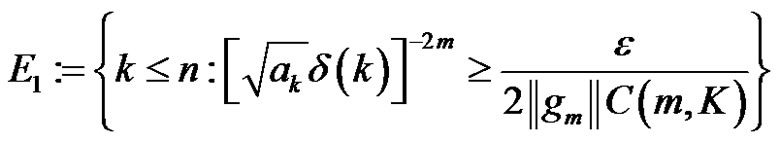
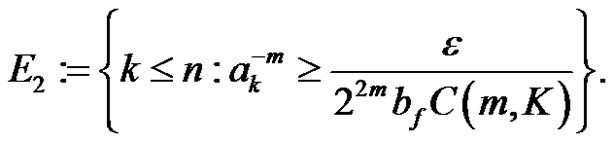
It is obvious that and δ(E) ≤ δ(E1) + δ(E2)
and δ(E) ≤ δ(E1) + δ(E2)
because of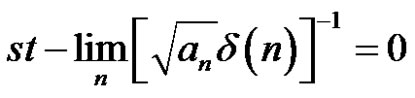 and
and .
.
The proof is completed.