Handwritten Character Recognition Using Multiresolution Technique and Euclidean Distance Metric ()
1. Introduction
The shape variation of handwritten characters causes the misclassification, therefore multiresolution of handwritten characters is important for the correct recognition. Using multiresolution we can reduce the size of characters without losing the basic characteristics of characters, therefore more accuracy and better recognition rate can be achieved using multiresolution. The extensive applications of Handwritten Character Recognition (HCR) in recognizing the characters in bank checks and car plates etc. have caused the development of various new HCR systems such as optical character recognition (OCR) system. There are so many techniques of pattern recognition such as template matching, neural networks, syntactical analysis, wavelet theory, hidden Markov models, Bayesian theory and minimum distance classifiers etc. These techniques have been explored to develop robust HCR systems for different languages such as English (Numeral) [1-3], Farsi [4], Chinese (Kanji) [5,6], Hangul (Korean) scripts [7], Arabic script [8] and also for some Indian languages like Devnagari [9], Bengali [10], Telugu [11- 13] and Gujarati [14]. HCR is an area of pattern recognition process that has been the subject of considerable research during the last few decades. Machine simulation of human functions has been a very challenging research field since the advent of digital computers [15]. The ultimate objective of any HCR system is to simulate the human reading capabilities so that the computer can read, understand, edit and do similar activities as human do with the text. Mostly, English language is used all over the world for the communication purpose, also in many Indian offices such as railways, passport, income tax, sales tax, defense and public sector undertakings such as bank, insurance, court, economic centers, and educational institutions etc. A lot of works of handwritten English character recognition have been published but still minimum training time and high recognition accuracy of handwritten English character recognition is an open problem. Therefore, it is of great importance to develop automatic handwritten character recognition system for English language. In this paper, efforts have been made to develop automatic handwritten character recognition system for English language with high recognition accuracy and minimum classification time. Handwritten character recognition is a challenging problem in pattern recognition area. The difficulty is mainly caused by the large variations of individual writing style. To get high recognition accuracy and minimum classification time for HCR, we have applied multiresolution technique using DWT [16,17] and EDM [18,19]. Experimental results show that the proposed method used in this paper for handwritten English character recognition is giving high recognition accuracy and minimum classification time. In what follows we briefly describe the different techniques used in our paper.
1.1. Multiresolution
Representation of images in various degrees of resolution is known as multiresolution process. “Inmultiresolution process, images are subdivided successively intosmallerregions [16,17]. Wavelets are used as the foundation of multiresolution process. In 1987, wavelets are first shown to be the foundation of a powerful new approach to signal processing and analysis called multiresolution theory [17]. Multiresolution theory is concerned with the representation and analysis of images at more than one resolution”. We use this technique in HCR system.
1.2. Euclidean Distance Metric
The EDM is significantly simplified under the following assumptions [18,19]:
• The classes are equiprobable.
• The data in all classes follow Gaussian distributions.
• The covariance matrix is the same for all classes.
• The covariance matrix is diagonal and all elements across the diagonal are equal.
Given an unknown pattern vector x, assign it to class 
if
EDM is often used, even if we know that previously stated assumptions are not valid, because of its simplicity. It assigns a pattern to the class whose mean is closed to it with respect to the Euclidean norm [20].
2. Methodology of the Proposed HCR System
This paper is divided into four sections. In Section 2.1, samples of handwritten characters are collected. In Section 2.2, some preprocessing steps are performed on the collected samples of handwritten characters. In Section 2.3, pattern vectors are generated using multiresolution technique by applying DWT on preprocessed handwritten characters. In Section 2.4, mean vectors are computed of each class and then EDM is used to compute distances from input pattern vector to all the mean vectors and input handwritten character is recognized by the minimum distance obtained in Section 2.4. A complete flowchart of handwritten English character recognition system is given in Figure 1 [21-23].
2.1. Data Collection
First of all, the data of English characters is collected in the written form on blank papers by people of different age groups. These characters are written by different blue/black ball point pens. The collected samples of handwritten characters are scanned by scanner into JPEG format on 600 ppi [24]. Then all the characters are separated and resized into 100 by 100 pixel images. The example of the samples of handwritten characters is given below (Figures 2 and 3).
2.2. Preprocessing
The separated RGB character images of 100 by 100 pixel resolution obtained in the Section 2.1 are converted into grayscale images and then the grayscale images is again converted into binary images using appropriate grayscalethresholding. Now, binary image is thinned using skeletonization infinite times. Edges of these thinned images are detected using appropriate thresholding and then further dilatedusing appropriate structure element [16,20,25]. These steps are known as preprocessing and preprocessing steps are given in Figure 4.
2.3. Feature Extraction
In this section, multiresolution technique is applied on the dilated images obtained in Section 2.2 and this is achieved by applying DWT [26,27]. In this section, pattern vectors are generated [28-30]. DWT has given good results in different image processing applications. It has excellent spatial localization and good frequency localization properties that makes it an efficient tool for image analysis. There are different multiresolution techniques such as image pyramids, subband coding and DWT. We have used DWT in this paper. DWT maps a function of a continuous variable into a sequence of coefficients. If the function being expanded is a sequence of numbers, like samples of a continuous function f(x, y), the resulting coefficients are called the DWT of f(x, y) [16,17]. DWT of an image f(x, y) of size MN is defined as
(1)
(2)
for 
and
(3)
where, 
is an arbitrary starting scale and
(4)
Figure 2. Sample of characters written by 10 different persons.
Figure 4. Results of preprocessing steps applying on a handwritten character.
and
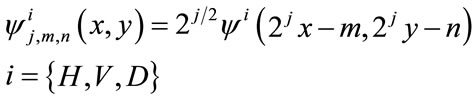(5)
where index i identifies the directional wavelets that assumes the values H, V and D. Wavelets measure functional variations such as intensity or gray-level variations for images along different directions. Directional wavelets are 
and
. 
measures variations along columns (like horizontal edges), 
measures variations along rows (like vertical edges) and 
measures variations along diagonals [16,17]. Equations (4) and (5) define the scaled and translated basis functions.
f(x, y), 
and 
are functions of the discrete variables x = 0, 1, 2, 3,
, M – 1 and y = 0, 1, 2, 3,
, N – 1. The coefficients defined in Equations (1) and (2) are usually called approximation and detail coefficients, respectively. 
coefficients define an approximation of f(x, y) at scale
. 
coefficients add horizontal, vertical and diagonal details for scales
. We normally let 
= 0 and select N
= M =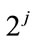
so that j = 0, 1, 2, 3,
, J – 1 and m, n = 0, 1, 2, 3, 
, 
[16,17]. Equation (3) shows that f(x, y) is obtained via the inverse discrete wavelet transform for given 
and 
of Equations (1) and (2). DWT can be implemented using digital-filters and down-samplers [16,17]. The block diagram of multiresolution using DWT is shown in the Figure 5.
We have used MATLAB toolbox for multiresolution by DWT [20]. DWT is applied three times successively on each dilated character image generated in the Section 2.2, and finally the reduced character image is captured into a bounding box using MATLAB toolbox and then, resized into 14 by 10 pixels image. The effect of multiresolution technique on a character obtained in Section 2 is given in the Figure 5.
2.4. Classification and Recognition
In this section, EDM is used to classify the input pattern vectors [31,32]. Pattern vectors generated in the Section 2.3 are grouped into 26 classes based on their similar
Figure 5. Character image after applying multiresolution and captured into bounding box.
properties. Each class contains pattern vectors, mean vector of each class is computed. We prepare a matrix whose rows are these mean vectors. Distance from input pattern vector to each mean vector is computed and minimum distance shows the class of input pattern vector to which it belongs [33-36]. Suppose, 
shows the pattern vector, 
shows the pattern class, 
shows the mean vector of jth class and 
shows the component of pattern vector. Mean vector is used as the representative of the class of vectors:
where, 
is the number of pattern vectors in the class 
and W is the number of pattern classes. Euclidean distance classifier is defined as:
where, x is the input pattern vector and 
is the distance from x to mean vector of the jth class. Input pattern vector x will belong to class wj if 
is the smallest distance [19,20].
3. Experimental Results
150 samples (3900 characters) were collected from 150 persons of different ages, 26 from each. First, 100 samples (2600 characters) were used to train the proposed HCR system and next 50 samples (1300 characters) were used to test the proposed HCR system. An analysis of experimental results has been performed and shown in Table 1 given below.
Here, we compare our results using the new approach with those of some other authors. The method used by Chen et al. [1] gets recognition rate of 92.20% for handwritten numerals. The method of Romero et al. [28] gets 90.20% recognition accuracy over the test data for handwritten numerals. The method of Mowlaei et al. [26] gets recognition rates of 92.33% and 91.81% for 8 classes of handwritten Farsi characters and numerals respectively.
4. Conclusion
From the above Table 1, we observe that the recognition
Table 1. The results showing the average recognition accuracy, here it is 90%.
accuracy is high for a particular level of multiresolution and appropriate resolution of input character images. When average recognition accuracy is optimal (maximum) for a particular level of multiresolution and appropriate resolution of character images, here it is 90%, then any further increment in the level of multiresolution results in the decrease of the average recognition accuracy. The resolution of input character image and the level of multiresolution are dependent upon each other so the challenge is to find appropriate relationship between them. Work is going on, we are trying to improve the recognition accuracy using some other methods and techniques such as fuzzy logic and hidden Markov models.