1. Introduction
We continue our study of the combinatorial properties of trinucleotide circular codes. A trinucleotide is a word of three letters (triletter) on the genetic alphabet . The set of 64 trinucleotides is a code in the sense of language theory, more precisely a uniform code, but not a circular code [1,2]. In order to have an intuitive meaning of these notions, codes are written on a straight line while circular codes are written on a circle, but, in both cases, unique decipherability is required.
. The set of 64 trinucleotides is a code in the sense of language theory, more precisely a uniform code, but not a circular code [1,2]. In order to have an intuitive meaning of these notions, codes are written on a straight line while circular codes are written on a circle, but, in both cases, unique decipherability is required.
Comma free codes, a very particular case of circular codes, have been studied for a long time, e.g. [3-5]. After the discovery of a circular code in genes with important properties [6], circular codes are mathematical objects studied in combinatorics, theoretical computer science and theoretical biology, e.g. [7-23].
There are 528 self-complementary circular codes of 20 trinucleotides [6,24,25] and, as proved here, they are naturally partitioned into two quite symmetric classes.
Let  be the four trinucleotides with identical nucleotides. In this paper, we study some particular partitions of
be the four trinucleotides with identical nucleotides. In this paper, we study some particular partitions of . Indeed, each circular code
. Indeed, each circular code  can be associated with two other subsets
can be associated with two other subsets  and
and  of
of  simply by operating two circular permutations of one letter and two letters on the trinucleotides of
simply by operating two circular permutations of one letter and two letters on the trinucleotides of . Then, we prove our main result, i.e. a circular code is self-complementary if and only if the remaining two classes are complement of each other. Furthermore, we also show that a subset of
. Then, we prove our main result, i.e. a circular code is self-complementary if and only if the remaining two classes are complement of each other. Furthermore, we also show that a subset of  is a circular code if and only if the set consisting of all its complements is a circular code.
is a circular code if and only if the set consisting of all its complements is a circular code.
As a consequence of these results, we also prove that if a circular code is self-complementary then either both its two conjugated classes are circular codes or none is a circular code.
In Section 2, we give the necessary definitions and a characterization for a set of trinucleotides to be a circular code. In Section 3, we give the results, mainly expressed by Proposition 7 and Proposition 8.
2. Definitions
The classical notions of alphabet, empty word, length, factor, proper factor, prefix, proper prefix, suffix, proper suffix, lexicographical order, etc. are those of [1]. Let  denote the genetic alphabet, lexicographically ordered with
denote the genetic alphabet, lexicographically ordered with . We use the following notation:
. We use the following notation:
•  (respectively
(respectively ) is the set of words (respectively non-empty words) over
) is the set of words (respectively non-empty words) over ;
;
•  is the set of the 16 words of length 2 (diletters or dinucleotides);
is the set of the 16 words of length 2 (diletters or dinucleotides);
•  is the set of the 64 words of length 3 (triletters or trinucleotides).
is the set of the 64 words of length 3 (triletters or trinucleotides).
We now recall two important genetic maps, the definitions of code and circular code, and the property of C3- self-complementarity for a circular code, in particular [1,6,17,24,25].
Definition 1. The complementarity map :
:  is defined by
is defined by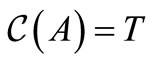 ,
,  ,
,  and
and , and by
, and by  for all
for all , e.g.,
, e.g., .
.
The map  on words is naturally extended to a word set
on words is naturally extended to a word set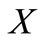 : its complementary trinucleotide set
: its complementary trinucleotide set  is obtained by applying the complementarity map
is obtained by applying the complementarity map  to all the trinucleotides of
to all the trinucleotides of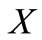 .
.
Definition 2. The circular permutation map :
:  permutes circularly each trinucleotide
permutes circularly each trinucleotide  as follows
as follows .
.
The map  on words is also naturally extended to a word set
on words is also naturally extended to a word set : its permuted trinucleotide set
: its permuted trinucleotide set  is obtained by applying the circular permutation map
is obtained by applying the circular permutation map 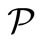 to all the trinucleotides of
to all the trinucleotides of . We shortly write
. We shortly write  for
for .
.
Definition 3. A set  of words is a code if, for each
of words is a code if, for each ,
,  , the condition
, the condition 
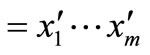 implies
implies  and
and  for
for .
.
Definition 4. A trinucleotide code  is circular if, for each
is circular if, for each ,
,  ,
,  ,
,  , the conditions
, the conditions  and
and  imply
imply ,
,  (empty word) and
(empty word) and  for
for  .
.
Definition 5. A trinucleotide code  is self-complementary if, for each
is self-complementary if, for each ,
,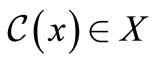 .
.
Definition 6. If  is a subset of
is a subset of , we denote by
, we denote by  the permuted trinucleotide set
the permuted trinucleotide set  and by
and by  the permuted trinucleotide set
the permuted trinucleotide set  and we call
and we call  and
and  the conjugated classes of
the conjugated classes of .
.
Definition 7. A trinucleotide circular code  is
is  - self-complementary if
- self-complementary if ,
, 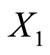 and
and  are circular codes satisfying the following properties:
are circular codes satisfying the following properties:  (self-complementary),
(self-complementary),  (and
(and ).
).
We have proved that there are exactly 528 self-complementary trinucleotide circular codes having 20 elements [6,24,25].
The concept of necklace was introduced by Pirillo [17] in order to characterize the circular codes for an efficient algorithm development. Let  be letters in
be letters in ,
,  diletters in
diletters in  and
and  an integer.
an integer.
Definition 8. Letter Diletter Continued Necklace (LDCN): We say that the ordered sequence  is an
is an  for a subset
for a subset  if
if
 and
and  .
.
Any trinucleotide set is a code (more precisely, a uniform code [1]) but only few of them are circular codes. We have the following proposition.
Proposition 1. [17] Let  be a trinucleotide code. The following conditions are equivalent:
be a trinucleotide code. The following conditions are equivalent:
1)  is a circular code;
is a circular code;
2)  has no 5LDCN.
has no 5LDCN.
The figure below explains the notion of 5LDCN.
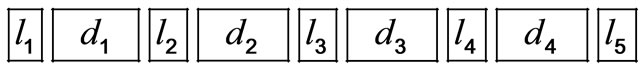
3. Results
Proposition 2. If  is a trinucleotide circular code having 20 elements and
is a trinucleotide circular code having 20 elements and  and
and 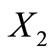 are its two conjugated classes then
are its two conjugated classes then ,
,  and
and  constitute a partition of
constitute a partition of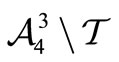 .
.
Proof. It is enough to prove that 
 . Suppose that the trinucleotide
. Suppose that the trinucleotide  belongs both to the classes
belongs both to the classes  and
and . Then
. Then  and
and  are both in class
are both in class . As no two conjugated trinucleotides can belong to a circular code, we are in contradiction. Suppose that the trinucleotide
. As no two conjugated trinucleotides can belong to a circular code, we are in contradiction. Suppose that the trinucleotide  belongs both to the classes
belongs both to the classes  and
and . Then
. Then  and
and  are both in class
are both in class . As no two conjugated trinucleotides can belong to a circular code, we are in contradiction. Suppose that the trinucleotide
. As no two conjugated trinucleotides can belong to a circular code, we are in contradiction. Suppose that the trinucleotide  belongs both to the classes
belongs both to the classes  and
and . Then
. Then  and
and  are both in class
are both in class . As no two conjugated trinucleotides can belong to a circular code, we are in contradiction. So,
. As no two conjugated trinucleotides can belong to a circular code, we are in contradiction. So, .
. 
Proposition 3. The class of self-complementary circular codes  with both
with both 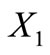 and
and  in the class of circular codes is non-empty.
in the class of circular codes is non-empty.
Proof. Consider, for example, the following set  of 20 trinucleotides
of 20 trinucleotides

It is enough to prove that  is a self-complementary circular code and that its two conjugated classes
is a self-complementary circular code and that its two conjugated classes  and
and  are also circular codes.
are also circular codes.
 is a self-complementary circular code.
is a self-complementary circular code.
 is self-complementary. Obvious by inspection.
is self-complementary. Obvious by inspection.
 is a circular code. We use Proposition 1 [17]. By way of contradiction, suppose that
is a circular code. We use Proposition 1 [17]. By way of contradiction, suppose that 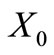 admits a 5LDCN. As
admits a 5LDCN. As  can be
can be ,
,  ,
,  or
or , it is enough to prove that each choice leads to a contradiction.
, it is enough to prove that each choice leads to a contradiction.
1) If  then there is no possible
then there is no possible  as
as  is not a suffix of any trinucleotide of
is not a suffix of any trinucleotide of , contradiction.
, contradiction.
2) If , there are three possible
, there are three possible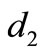 :
:
• if  (a) or
(a) or  (b) then
(b) then  (c) but there is no possible
(c) but there is no possible  as
as  is not a prefix of any trinucleotide of
is not a prefix of any trinucleotide of , contradiction
, contradiction
• if  (d), there is a contradiction as no trinucleotide of
(d), there is a contradiction as no trinucleotide of  has a prefix
has a prefix .
.
3) If , there are six possible
, there are six possible :
:
• if  or
or , contradiction (a) and (b)
, contradiction (a) and (b)
• if 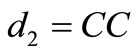 then
then , contradiction (c)
, contradiction (c)
• if  or
or  then
then 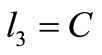 or
or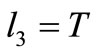 :
:
if , there are three possible
, there are three possible : if
: if  or
or  then
then , similarly to (c), contradiction, and if
, similarly to (c), contradiction, and if , similarly to (d), contradiction
, similarly to (d), contradiction
if , contradiction (c)
, contradiction (c)
• if , contradiction (d).
, contradiction (d).
4) If , similarly to (c), contradiction.
, similarly to (c), contradiction.
As, for each letter, we cannot complete the assumed 5LDCN for , we are in contradiction. Hence,
, we are in contradiction. Hence,  is a circular code.
is a circular code.
 is a circular code. We have to prove that
is a circular code. We have to prove that

is a circular code. By way of contradiction, assume that  admits a 5LDCN.
admits a 5LDCN.
1) If , there are four possible
, there are four possible :
: ,
,  ,
,  and
and , but no possible
, but no possible , contradiction.
, contradiction.
2) If , there are three possible
, there are three possible :
: ,
,  and
and , but no possible
, but no possible , contradiction.
, contradiction.
3) If , there are six possible
, there are six possible :
: ,
,  and
and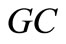 , and the cases
, and the cases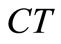 ,
,  and
and  already seen, but no possible
already seen, but no possible , contradiction.
, contradiction.
4) If , there is no possible
, there is no possible , contradiction.
, contradiction.
Hence,  is also a circular code.
is also a circular code.
 is a circular code. Finally, we have to prove that
is a circular code. Finally, we have to prove that

is a circular code. By way of contradiction, assume that  admits a 5LDCN.
admits a 5LDCN.
1) If , there is no possible
, there is no possible , contradiction.
, contradiction.
2) If , there are six possible
, there are six possible :
: ,
,  ,
,  ,
,  ,
,  and
and , but no possible
, but no possible , contradiction.
, contradiction.
3) If , there are three possible
, there are three possible :
: ,
,  and
and  which are cases already seen, contradiction.
which are cases already seen, contradiction.
4) If , there are four possible
, there are four possible :
: ,
,  ,
,  and
and , but no possible
, but no possible , contradiction.
, contradiction.
Hence, as  and
and ,
,  is also a circular code.
is also a circular code. 
Proposition 4. The class of self-complementary circular codes  having 20 elements with neither
having 20 elements with neither 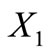 nor
nor  in the class of circular codes is non-empty.
in the class of circular codes is non-empty.
Proof. Consider, for example, the following set  of 20 trinucleotides
of 20 trinucleotides

It is enough to prove that  is a self-complementary circular code and that neither its conjugated class
is a self-complementary circular code and that neither its conjugated class  nor its conjugated class
nor its conjugated class  are circular codes.
are circular codes.
 is a self-complementary circular code.
is a self-complementary circular code.
 is self-complementary. Obvious by inspection.
is self-complementary. Obvious by inspection.
 is a circular code. We use Proposition 1 [17]. By way of contradiction, assume that
is a circular code. We use Proposition 1 [17]. By way of contradiction, assume that  admits a 5LDCN.
admits a 5LDCN.
1) If  then there is one possible
then there is one possible  but no possible
but no possible , contradiction.
, contradiction.
2) If , there are two possible
, there are two possible :
:
• if  then
then  (a) and
(a) and  (b) but there is no possible
(b) but there is no possible , contradiction
, contradiction
• if  (c) then there is no possible
(c) then there is no possible , contradiction.
, contradiction.
3) If  we have seven possible
we have seven possible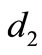 :
:
• if  then
then  or
or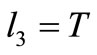 :
:
if  (d) then
(d) then  or
or :
:
- if  then
then  and
and  but there is no possible
but there is no possible , contradiction
, contradiction
- if  then there is no possible
then there is no possible , contradiction
, contradiction
if , contradiction (a)
, contradiction (a)
• if , similarly to (b), contradiction
, similarly to (b), contradiction
• if ,
,  or
or  then
then , contradiction (a)
, contradiction (a)
• if  then
then  or
or , contradiction (a) and (d)
, contradiction (a) and (d)
• if , contradiction (c).
, contradiction (c).
4) If , similarly to (a), contradiction.
, similarly to (a), contradiction.
Hence,  is a circular code.
is a circular code.
 is not a circular code. We have
is not a circular code. We have

We use a technique developed in [23]. Observe that  contains
contains  So,
So,
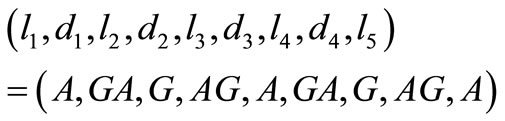
is a 5LDCN for this 4-element subset of  and, a fortiori, for
and, a fortiori, for  itself which, consequently, is not a circular code.
itself which, consequently, is not a circular code.
 is not a circular code. We have
is not a circular code. We have

We again use a technique developed in [23]. Remark that  contains
contains . So,
. So,

is a 5LDCN for this 4-element subset of  and, a fortiori, for
and, a fortiori, for  itself which, consequently, is not a circular code.
itself which, consequently, is not a circular code. 
We need the propositions hereafter and, in particular the following one which states a general property of the involutional antiisomorphisms such as the complementary map .
.
Proposition 5. A subset  of
of  is a circular code if and only if
is a circular code if and only if  is a circular code.
is a circular code.
Proof. Suppose, first, that  is not a circular code and that
is not a circular code and that  is a circular code. So
is a circular code. So  has a 5LDCN. This means that there are 13 nucleotides, say
has a 5LDCN. This means that there are 13 nucleotides, say
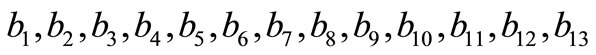
such that the trinucleotides
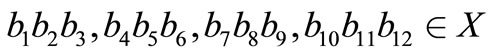
and
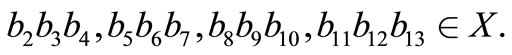
Now, consider the sequence

All the following trinucleotides belong to :
:
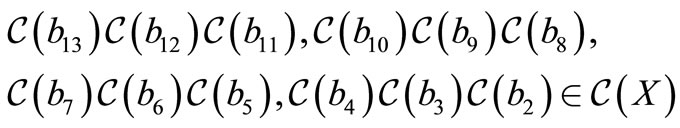
and
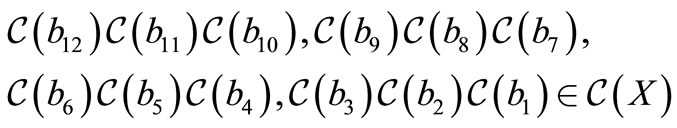
as they are the complement of trinucleotides in . So,
. So,  admits a 5LDCN and it cannot be a circular code. Contradiction.
admits a 5LDCN and it cannot be a circular code. Contradiction.
The case  is a circular code and
is a circular code and  is not a circular code is similar.
is not a circular code is similar. 
Proposition 6. Let  be a self-complementary subset of
be a self-complementary subset of . If
. If  is partitioned into three classes such that two of them are the complement of each other then necessarily the third one is self-complementary.
is partitioned into three classes such that two of them are the complement of each other then necessarily the third one is self-complementary.
Proof. Let ,
,  and
and  be the three classes of an arbitrary partition of
be the three classes of an arbitrary partition of  and suppose that
and suppose that  and
and  are complementary, i.e.
are complementary, i.e.  and
and  satisfy
satisfy . Let
. Let  be a trinucleotide of
be a trinucleotide of . We claim that
. We claim that . Indeed, in the opposite case,
. Indeed, in the opposite case,  should not be the complement of
should not be the complement of  because
because . We also claim that
. We also claim that . Indeed, in the opposite case,
. Indeed, in the opposite case,  should not be the complement of
should not be the complement of  because
because . It remains the case
. It remains the case . So,
. So,  is self-complementary.
is self-complementary. 
Remark 1. Clearly, if ,
,  and
and  constitute an arbitrary partition of
constitute an arbitrary partition of  then the self-complementarity of
then the self-complementarity of  is not enough to ensure that
is not enough to ensure that  and
and  are complementary of each other. This remark is again true if, in addition,
are complementary of each other. This remark is again true if, in addition,  is a self-complementary circular code having 20 elements. Indeed in this case, it is easy to make a partition
is a self-complementary circular code having 20 elements. Indeed in this case, it is easy to make a partition  in two classes
in two classes  and
and  that are not complementary of each other. Any case, if we consider the partition of
that are not complementary of each other. Any case, if we consider the partition of  in the three classes given by a self-complementary trinucleotide circular code
in the three classes given by a self-complementary trinucleotide circular code  having 20 elements and by its two conjugated classes
having 20 elements and by its two conjugated classes  and
and  then the necessary and sufficient condition holds (Proposition 7 below).
then the necessary and sufficient condition holds (Proposition 7 below).
Proposition 7. A trinucleotide circular code  having 20 elements is self-complementary if and only if
having 20 elements is self-complementary if and only if  and
and  are complement of each other.
are complement of each other.
Proof if part. It is a trivial consequence of Proposition 6.
Only if part. Suppose that  is self-complementary and consider the partition
is self-complementary and consider the partition ,
, 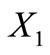 and
and  of
of . Suppose that the trinucleotide, say
. Suppose that the trinucleotide, say , belongs to
, belongs to . Then, also
. Then, also
 .
.
We have
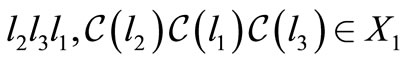
and
 .
.
As  is a generic trinucleotide of
is a generic trinucleotide of  and as
and as
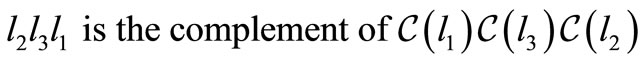
and
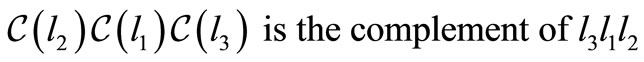
then  is the complement of
is the complement of .
. 
As a consequence, we have the following proposition.
Proposition 8. If a trinucleotide circular code  having 20 elements is self-complementary then either 1)
having 20 elements is self-complementary then either 1)  and
and  are both circular codes or 2)
are both circular codes or 2)  and
and  are not circular codes (both have a necklace).
are not circular codes (both have a necklace).
Proof. We have four possibilities:
 is a circular code and
is a circular code and 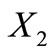 is a circular code;
is a circular code;
 is a circular code and
is a circular code and  is not a circular code;
is not a circular code;
 is not a circular code and
is not a circular code and  is a circular code;
is a circular code;
 is not a circular code and
is not a circular code and  is not a circular code.
is not a circular code.
Now, by applying Propositions 3 and 4, we have that the first and the last possibilities can be effectively realized.
Suppose that, by way of contradiction, the second possibility is realized. So,  is a circular code. By Proposition 7, we have
is a circular code. By Proposition 7, we have . So, by Proposition 5,
. So, by Proposition 5,  must also be a circular code. Contradiction.
must also be a circular code. Contradiction.
Suppose that, by way of contradiction, the third possibility is realized. So,  is a circular code. By Proposition 7, we have
is a circular code. By Proposition 7, we have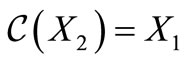 . So, by Proposition 5,
. So, by Proposition 5, 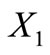 must also be a circular code. Contradiction.
must also be a circular code. Contradiction.
So, only the first and the last possibilities can occur. 
Hence, our proposition holds.
Proposition 9. The 528 self-complementary circular codes having 20 elements are partitioned into two classes: one class contains codes with the two permuted sets  and
and  which are both circular codes while the other class contains codes with the two permuted sets
which are both circular codes while the other class contains codes with the two permuted sets  and
and  which both are not circular codes.
which both are not circular codes.
Proof. It is enough to apply Proposition 8 to each of the 528 trinucleotide circular codes having 20 elements. 
4. Acknowledgements
We thank Jacques Justin for his advices. The second author thanks the Dipartimento di matematica U. Dini for giving him a friendly hospitality.