Abstract

Periods are algebraic integrals, extending the class of algebraic numbers, and playing a central, dual role in modern Mathematical-Physics: scattering amplitudes and coefficients of de Rham isomorphism. The Theory of Periods in Mathematics, with their appearance as scattering amplitudes in Physics, is discussed in connection with the Theory of Motives, which in turn is related to Conformal Field Theory (CFT) and Topological Quantum Field Theory (TQFT), on the physics side. There are three main contributions. First, building a bridge between the Theory of Algebraic Numbers and Theory of Periods, will help guide the developments of the later. This suggests a relation between the Betti-de Rham theory of periods and Grothendieck’s Anabelian Geometry, towards perhaps an algebraic analog of Hurwitz Theorem, relating the algebraic de Rham cohomology and algebraic fundamental group, both pioneered by A. Grothendieck. Second, a homotopy-homology refinement of the Theory of Periods will help explain the connections with quantum amplitudes. The novel approach of Yves Andre to Motives via representations of categories of diagrams, relates from a physical point of view to generalized TQFTs. Finally, the known “universality” of Galois Theory, as how symmetries “grow”, controlling the structure of the objects of study, is discussed, in relation to the above several areas of research, together with ensuing further insight into the Mathematical-Physics symbiosis. To better understand and investigate Kontsevich-Zagier conjecture on abstract periods, the article ponders on the case of algebraic Riemann Surfaces representable by Belyi maps. Reformulation of cohomology of cyclic groups as a discrete analog of de Rham cohomology and the Arithmetic Galois Theory will provide a purely algebraic toy-model of the said algebraic homology/homotopy group theory of Grothendieck as part of Anabelian Geometry. The corresponding Platonic Trinity 5,7,11/TOI/E678 leads to connections with ADE-correspondence, and beyond, e.g. Theory of Everything (TOE) and ADEX-Theory. In perspective of the “Ultimate Physics Theory”, quantizing “everything”, i.e. cyclotomic quantum phase and finite Platonic-Hurwitz geometry of qubit frames as baryons, could perhaps be “The Eightfold (Petrie polygon) Way” to finally understand what quark flavors and fermion generations really are.

Keywords

Periods, Anabelian Geometry, Motives, Quantum Physics

Share and Cite:

1. Introduction

Periods are a new class of numbers represented by algebraic integrals, extending the class of algebraic numbers and pervasive in applications, notably appearing as scattering quantum amplitudes. Their study was stimulated by the relatively recent work of Kontsevich and Zagier [1], following the programmatic paper relating them with Motives and Deformation Quantization in [2].

Author’s preliminary efforts to understand the “core” of this network of ideas, including [3] [4], with focus on the relation between Periods, as coefficients of the period isomorphism, and scattering amplitudes [5] - [10] lead to the present viewpoint, regarding the relation to Motives, as suggested by the following diagram:

1.1. The Main Ideas: An Overview

There are three key ideas and directions of development, as principal contributions within this article.

First, the study of the relation between the Theory of Algebraic Numbers and Theory of Periods provides a foundational bridge, which will help guide the developments of the later. A starting point is to conduct a study of Riemann surfaces over $\bar{Q}$ that admit a Belyi map, and to understand the relations between abstract periods and motives via Dessins D’Enfants §2.2.2.

Second, the article emphasises the need for a homotopy-homology refinement of the Theory of Periods, which helps explain the connections with quantum amplitudes. Recall that Feynman Integrals representing these, are related to Chen Iterated Integrals, which were historically playing the role of a homotopical de Rham Theory, and which in a similar way to the prototypical Hurwitz Theorem, should be tentatively related to the algebraic de Rham cohomology, hence to the Theory of Periods. The homotopical aspects are clearly present in Grothendieck’s developments of the algebraic de Rham cohomology theory establishing the theory of an algebraic fundamental group, towards a “general Galois Theory” as part of the so called Anabelian Geometry [11].

This later connection will allow to understand, for example, the novel approach of Yves Andre to Motives [12], via representations of categories of diagrams, from a physical point of view of a generalized Topological Quantum Field Theory, in the sense of Atiyah [13], and generalized by the present author [14]. As a hint for now, Chow motives can be envisioned as “embedded cobordisms”, and associated integrals, the periods as de Rham isomorphism coefficients, as numerical “shadow” of TQFT amplitude. This analogy will be pursuit and documented elsewhere.

Finally, the known “universality” of Galois Theory, as how symmetries “grow”, controlling the structure of the objects of study, is discussed, in relation to the above several areas of research, together with ensuing further insight into the Mathematical-Physics symbiosis. A simple and elementary example of this universality is Arithmetic Galois Theory, in the context of finite abelian groups, and formulated in the language of Category Theory [15] [16]. Its relation with a discrete version of algebraic de Rham cohomology, as suggested in [17] from the cohomological side, deserves, and will be the subject of a separate article.

The ideas and specific problems to be studied to make this correspondence more precise, are presented below.

Further speculations and questions, regarding important related problems in Physics, notably the corresponding Platonic Trinity 5,7,11/TOI/E678 leads to connections with ADE-correspondence, and beyond, e.g. TOEs and ADEX-Theory [18], are included for future reference. The appearance of Platonic groups of symmetries, should not be surprising at this stage; in interests of physicists in finite groups of symmetry as vertical gauge groups dates since the 1950s. In perspective of the “Ultimate Physics Theory”, quantizing “everything”, i.e. cyclotomic quantum phase and finite Platonic-Hurwitz geometry of qubits/baryons, could perhaps be “The Eightfold (Petrie polygon) Way” to finally understand what quark flavors and fermion generations really are.

1.2. Nomenclature

To help the reader skim through the paper, a list of the main mathematical objects involved, and associated notation used, is briefly explained below.

· The abstract periods of an algebraic variety X are denoted by $Per\left(X\right)$ ; $\gamma$ is a singular chain and $D=\partial \gamma$ a divisor. The corresponding pair is denoted $\left(X\mathrm{,}D\right)$, or the full abstract period, denoted as $\left(X\mathrm{,}D\mathrm{,}\omega \mathrm{,}\gamma \right)$, where $\omega$ is the algebraic form whose integral ${\displaystyle {\int }_{\gamma }\omega }$ yields the corresponding numeric period;

· $\Gamma$ refers to a finite subgroup of for example the modular group $S{L}_2\left(Z\right)$ ;

· A meromorphic map $f\mathrm{<mo>\; :\; </mo>}X\to S^2$, from a Riemann surface to the Riemann sphere (also denoted as $C{P}^1$, the complex projective space), is viewed as a ramified cover; if satisfying the conditions of Belyi Theorem, the corresponding Belyi map is rather viewed as a pair $\left(X\mathrm{,}f\right)$ (the alternative notation Belyi in the place of f is meant to suggest this).

Various other variables, parameters etc. are rather secondary, and maybe skipped when skimming through the article. Consultation of the references cited will provide the additional details, if the reader is interested in pursuing the idea.

The Kontsevich conjecture on abstract periods is related to Grothendieck’s Conjecture [19], and by considering the special case of Riemann Surfaces representable by Belyi maps [20], which started Grothendieck on his long march on Galois Theory [21] [22], it is expected to obtain additional insight and perhaps a proof in a special case.

It is remarkable its deep relation to Galois Theory [23], hence with algebraic numbers, as “classical periods”, as well as a plethora of other “essential ingredients”: Dessins d’Enfants, cartographic maps, matrix integrals, moduli spaces, Kontsevich model, chord diagrams etc., conform Lando and Zvonkin book [24].

2.1. Trends and State-of-the-Art of Research on Periods

An update of the research on periods was in order, highlighting some points to be investigated.

2.1.1. Period Identities, Hilbert’s 3rd Problem and Dehn Invariants

In the concrete direction for studying periods, the work of Juan Viu-Sos for example [25], reduces periods ${\displaystyle {\int }_D\omega }$ to geometric volumes ${\displaystyle {\int }_{Semi-Alg}}Vol$ of semi- algebraic sets (see also [26], in an analysis in the sense of measure theory, to better understand the limit process from finite-additive to $\sigma$ -additive. In some sense this is going “back-in-time” to Lebesgue and Borel, but notably under the guidance of Hilbert (3rd Problem).

It is notable, and worth investigate how Dehn surgery and invariants enter the picture. The reason is, that Dehn surgery provide (perhaps) an alternative description of how to build/glue a manifold, capturing Betti homology in a homotopical way. Does this refine the homological period isomorphism?

Additional references to be investigated are listed in [26], notably those presenting work by Waldshmidt and Yushinava.

The difficulty of this line of investigation lies on the “forgetting structure” when going from a categorical point of view to a “Cauchy/numerical-methods/algorithmic” approach for the real numbers: $R\mathrm{<mo>\; /\; </mo>}\bar{Q}$ is a difficult to understand object, conform with Grothendieck’s Conjecture ( [19], p. 2):

$\text{Transcendental}\text{Degree}\left[Per\left(X\right)/Q\right]=Dim\left(\text{Motivic}\text{Galois}\text{group}\right)\mathrm{.}$

2.1.2. … And Grothendieck’s Conjecture

In the conceptual direction, Grothendieck’s initial work on periods, he first introduced the algebraic de Rham cohomology to “organise” periods into an algebraic structure, and then the work evolved into Anabelian Geometry, around the algebraic fundamental group, and a general “Galois Theory”:

Motivic Galois Groups ↔ Algebraic Fundamental Groups?

With Chen Iterated Integrals as a homotopic version of de Rham Theory, and hence the well-known connections with MZVs, Feynman Integrals etc. the relation between the two topics, algebraic cohomology/fundamental group, requires further investigations in this direction.

2.1.3. Why Belyi Ramified Covers

It is natural to look at Belyi ramified covers of the Riemann sphere with a Mobius homological mark-up ( $S{L}_2\left(C\right)$ /“conformal group base point”): this (Belyi’s Theorem) was Grothendieck “turning moment” (letter to Faltings).

Ajub’s geometric conjecture (loc. cit. §5, Th. 40, p. 7) seems to compare the algebraic fundamental group of a field extension and the relative motivic group. The take from this, is the relevance of the homologic/homotopic algebraic de Rham/Chen framework, probably subject to a version of “Hurwitz Theorem” [4].

2.2. Is There a Ramification Theory of Periods?

In view of the tight connections between algebraic numbers and periods, it is worth strengthening the analogy: “Is there a Ramification Theory for Periods?”.

2.2.1. Periods: “Numbers” or “Functions”?

Note that “numbers”, like the algebraic i, have geometric interpretations (a la

Klein geometry [27]), e.g. rotation by $\frac{1}{4}\cdot 2\pi$, the fundamental period $2\pi$ ; i.e.

the representation point of view is more lucrative, hence so is Galois Theory, complementing Archimedes’ Cauchy-like approximation of $\pi$.

On this dichotomy (numbers vs. functions), see also [28].

2.2.2. The Category of Ramified Belyi Covers

Consider Belyi maps for Riemann surfaces defined over the rationals, in analogy to covering maps and their deck transformations, or field extensions and Galois groups.

Then a morphism of Belyi maps can be viewed as a morphism of Riemann surfaces compatible with the corresponding ramified covers defined by the Belyi maps $B_i$ :

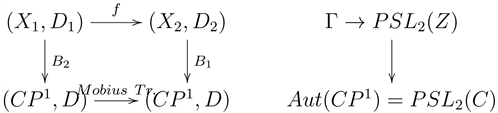
Here $D=\left\{\mathrm{0,1}\right\}$ is the standard divisor on the Riemann sphere $S^2=C{P}^1$, with standard chain, the cut $\gamma =\left[\mathrm{0,1}\right]$. Associated to these, on the Riemann sphere side, we have the standard period $2\pi$ and logarithm $log\left(z\right)$.

On the “other side” of the ramified cover X, we have the corresponding Dessin D’Enfant ${\gamma }_i=B_i^{-1}\left(\gamma \right),i=1,2$, with their boundaries, the divisors $D_i=\partial {\gamma }_i,i=1,2$ [24]. A study of how the Dessin D’Enfant determines (relates to) the periods of Riemann surfaces, would be a starting point for a better understanding of periods, in the above sense. The morphisms (via Hurwitz Theorem) are an analog of covering maps/field extensions, and could lead to a Galois Theory for Belyi Ramified Covers, Jacobian varieties, period isomorphisms for $X_i$ :

Dessins D’Enfant & Jacobian Periods?

Remark 2.1. More generally, one can consider a category of epi’s/mono’s, the torsor of its associated subgroupoid, and a pair of adjoint functors, playing the role of a Galois Connection, in order to derive the “absolute theory” at Categorical Theory level, as a “tool-box”. It may lead to connections between motives and the theory of generalized cohomology theories (P. Hilton [29]), via triples and spectra.

2.2.3. The Relation with KZ-Moves

Linearity and Stokes Theorem are captured by considering the period isomorphism. The “change of variables” (diffeo/biholomorphic) is built in the formalism of differential forms.

Hence, it seems that the essential part of the KZ-moves, modulo the torsor structure due to equivalence via isomorphisms, is the way the period isomorphism behaves under a ramified cover.

For covering maps this would correspond to the lattice structure of the fundamental group of the base space, via its universal covering map:

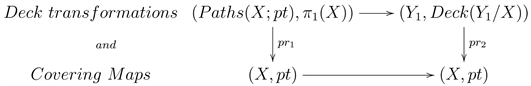
On the other hand a differential form, e.g. a 1-form in our case, defines a monodromy, and therefore a ramified cover via path integral lifting. How all these relate to periods remains to be seen…

2.2.4. Prime Decomposition and Ramification of Dessins D’Enfant?

The ramification process (and theory) should go parallel to the ramification of primes under field extensions:

$Alg\mathrm{.}N\mathrm{.}T\mathrm{.\; <mo>\; :\; </mo>}e\mathrm{,}f\mathrm{,}gI\to D\to Gal\left(F_{p^f}/F_p\right)\stackrel{}{\leftrightarrow }Mor\mathrm{<mo>\; :\; </mo>}\left(X\mathrm{,}Bely{i}_1\right)\to \left(X_2\mathrm{,}Bely{i}_2\right)$

Remark 2.2. The theory is about Spec of Z-Mod and Spec(Z) (primes)…

The decomposition of primes is controlled by the structure of the Galois group (e.g. abelian case/cyclotomic $K=Q\left({\zeta }_n\right)$ : $Gal\cong Z/n^{\times }$ and orbit decomposition of the “space” Z/n; ramification: multiplier by p dividing n, i.e. quotients/reso- nance/substructure).

Note that restricting to 3-ramified points (Belyi maps), restricts the degrees of freedom of the lifting process.

2.2.5. Rigidity vs. Continuous Parameters

Specifically, consider the periods represented by quadruples $\left(X\mathrm{,}D\mathrm{,}\omega \mathrm{,}\gamma \right)$ defined on Riemann surfaces having an algebraic numbers model over $\bar{Q}$, with a Belyi map [24], p. 79:

$\text{Belyi}\text{Map}\mathrm{<mo>\; :\; </mo>}f\mathrm{<mo>\; :\; </mo>}X\to C{P}^1\left(\text{3-points}\text{ramified}\text{covers}\right)\mathrm{.}$

This case exhibits a rigidity (lack of a continuous parameter) [24], p. 76), which hints towards a connection with braids representations, KZ-equations, MZVs etc. [30], essential concepts from the “Number Theory Side” of Feynman Integrals as amplitudes.

The case of higher number of ramification points probably corresponds to families of periods indexed by parameters.

2.2.6. Homological vs. Homotopical

An investigation of the Conjecture will start from understanding the relation between these periods and the “discrete DATA” (Dessins D’Enfants), as a homotopical analog of the Hodge structure characterizing the Betti-de Rham homological period isomorphism.

The pertaining goal is to identify a more tangible combinatorial structure that corresponds to periods, invariant under a different kind of “moves” (e.g. Pachner moves, Rademeister moves, chord diagrams relations etc.) and allow for a correspondence with the 3-moves of Kontsevich’s Conjecture.

Byproduct of the study would be a better understanding of the relation between “homological” and “homotopical” periods, as intuitively corresponding to the “abelian vs. anabelian” case.

Indeed, Galois groups controlling algebraic numbers, as a special case of algebraic fundamental groups, are special cases of periods, controlled by the algebraic de Rham cohomology. But these two algebraic theories should be related by an analog of Hurwitz Theorem, as intuitively “hoped” by the present author in the IHES talk [4].

2.2.7. A Study of Periods of Elliptic Curves

Conform Polya’s advise “If you can’t solve a problem, there is an easier one you can’t solve; find it!” [31], this could be the specific study which could yield a better understanding of the basic concepts, and of the relations between them.

In this case, the periods are related by the Legendre relation [32] [33] [34] [35]:

$det{\left[{\displaystyle {\int }_{{\gamma }_i}{\omega }_j}\right]}_{i\mathrm{,}j=1,2}=2\pi i\mathrm{.}$

2.2.8. … And Beyond: Hurwitz Surfaces

The case of Hurwitz Surface $X\to S^2$, maximizing the automorphism group is even more interesting to study, as it corresponds to Belyi maps with 3-ramification points of orders 2, 3 and 7 [36], and has applications to Finite String Theory: modeling baryons as finite Hopf fibrations (finite qubits), with Platonic tessellations (to be explained later on).

The “higher genus Platonic solids”:

$\begin{array}{l}\text{Genus}g\text{Platonic}\text{Riemann}\text{Surfaces}\mathrm{<mo>\; :\; </mo>}M\left(g\mathrm{<mo>\; ;\; </mo>}n\right)={\mathcal{H}}_{+}/\Gamma \mathrm{,}\\ \Gamma \left(\mathrm{2,}k\mathrm{,}l\right)\text{-triangle}\text{group}\mathrm{,}\end{array}$

some of which attain their Hurwitz bound $84\left(g-1\right)=2\cdot \left|\xi \left(M\right)\right|\left|S_4\right|$, are good candidates for symmetry of fundamental stringy states, provide a mathematical framework where “Finite String Theory meets the Standard Model on the Quantum Computing ground”.

More specifically, the notable cases of automorphism groups $PS{L}_2\left(F_p\right)\mathrm{,}p=\mathrm{5,7,11}$ (Dodecahedron $g=0$, Klein quintic $g=3$ etc.) is important in view of crepant resolutions of orbifolds $C^2/\Gamma$, for finite subgroups of rotations $\Gamma$ (Mckay/ADE correspondence).

2.2.9. Periods of the Klein Quartic and Belyi, Galois, Gauss Etc

Klein’s quartic is a very good example to see how the geometry, with group theory aspects, relates to algebra (Galois action) and the analytic (the Jacobian) [37].

The maps from Klein’s quartic to tori:

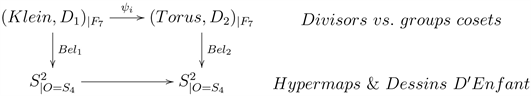
are related to Belyi maps presentations (loc. cit. §4.2) in terms of edges of tessellations or cuts with their associated divisors, providing a better understanding of the geometric aspects, coming from the Platonic tessellations, and the analytic aspects (1-forms, Betti bases and periods)¹.

Other good examples, include two genus two RS with Platonic tessellations (cyclotomic over $Q\left({\zeta }_5\right)$ ). For example, the basis for the lattice of periods computed loc. cit. p. 44:

$1+{\zeta }^2-{\zeta }^3-{\zeta }^4\mathrm{,}-1+{\zeta }^3+{\zeta }^4-{\zeta }^5\mathrm{,}$

should be related to Gauss/Kummer periods (see Klein’s map).

The case of Fermat surfaces $x^k+y^k+z^k$, also Platonic, invite to a study the connections with Weyl Conjectures, zeros and the corresponding Riemann Hypothesis (now a Theorem).

The pair of pants decomposition of Riemann surfaces [37] §5, could be related to the “Ramification Theory”, alluded to earlier, when related to Belyi maps. It is reminiscent of coproducts, as for instance in Frobenius algebras characterizing 2D-TQFTs, and of CFTs.

2.3. Klein Quartic, String Theory and Elementary Particles

These Riemann-Platonic surfaces, with tessellations reminiscent of lattices playing a crucial role in Algebraic Number Theory (lattice models of finite fields), and Algebraic Geometry (Hodge theory: Betti vs. de Rham structures), not clear how related to Belyi (hyper)maps, have symmetry groups which are related to the finite Hopf sub-bundles, derived from $S^1=U\left(1\right)$ circle or $S^3=SU\left(2\right)$ monopole bundles.

Applications to the Standard Model

Taking the Klein quartic as an example of a Platonic-Riemann Surface that is Hurwitz, defined by the fundamental invariant polynomial $\Phi =x{y}^3+y{z}^3+z{x}^3=0$ (usually denoted by ${\Phi }_4$ [38]):

opens the “right” way to understand elementary Particles and their mass:

The Eightfold (Petrie) Way!

with $SU\left(3\right)$ playing the role of a Galois group, and quiver representations refining Gell-Man’s 8-fold way via Gabriel’s Theorem [39] [40].

3. From Periods to Anabelian Geometry

This suggests a relation between the theory of homological periods and Grothen- dieck’s Anabelian Geometry, towards perhaps of an algebraic analog of Hurwitz Theorem, relating the the algebraic de Rham cohomology and algebraic fundamental group, both pioneered by A. Grothendieck in Esquisse d’un Programme [11].

Indeed, as early as during the previous visit, the author suggested a “Hurwitz Theorem” larger framework surrounding the theory of abstract periods, motives and Galois Theory, as presented in [4]:

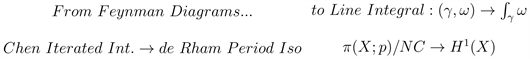
One would view $\gamma$ as a cobordism, $\omega$ as a propagator and ${\displaystyle {\int }_{\gamma }\omega }$ as an amplitude (work/circulation); ${\pi }_1\left(X\right)$ as a groupoid makes sense and a “physical form” of Hurwitz Theorem seams to “refine” the period isomorphism.

According to the philosophy of Anabelian Geometry, “What is being represented here as space with this algebraic fundamental group?” (Compare with 1-forms defining connections whose monodromy define a representation of the fundamental group). Then a natural question arises: “What is the underlying Representation Theorem, with the classical models of Pontryagin and Tannaka-Krein duality in mind, in the general framework of Yoneda Representation Theorem.

3.1. A Physics Interpretation of Period, and Montonen-Olive/T-Duality

Periods ${\displaystyle {\int }_{\gamma }\omega }$ can be interpreted along the following lines, as follows; we will be specific: 1D-case of Riemann surfaces.

3.1.1. Closed vs. Open Periods; Electric vs. Magnetic

The flow of the 1-form, which mathematically measures the geometric object $\gamma$ with boundary $D=\partial \gamma$, can be viewed as the work/flux of a “probe” in the dynamics defined by the 1-form.

Its poles and zeros have charges: electric charges are the residues ${\displaystyle {\int }_{S^1\left(p\right)}\omega }$ (Gauss Law; circle around point p), while the periods are magnetic charges ${\displaystyle {\int }_{\gamma }\omega }$, in a homological basis ${\gamma }_i$.

There are relations between charges, and Riemann-Roch Theorem restricts the possible dynamics.

3.1.2. Helmholtz/Hodge and “Maxwell’s Equations”

The Hodge duality corresponds to Helmholtz Decomposition. It hints to the fact that it reflects the structure of the group of symmetries of the space X (“Gauge group”):

translations/grad, rotations/curl, similarities/divergence.

The local group is conformal, with its polar decomposition; the “global aspects” are captured by the fundamental group ${\pi }_1\left(X\right)$ (“Galois Group”).

Correspondingly there is an underlying “gauge theory” with connection 1-form $\omega$, and hence a Motonen-Olive Duality between “electric” and “magnetic”, which in String Theory corresponds to T-Duality.

The point is that the physical interpretation complements a “purely Gro- thendieck” approach for understanding periods, paving the road towards understanding Feynman Integrals, and more importantly, intrinsic scattering amplitudes (to be made precise in view of the new methods for computing MHV amplitudes [41]).

3.2. … And Quantum Physics Amplitudes (beyond Veneziano)

There seems to be good prospects of better understanding the role of absolute Galois group in the physics context of scattering amplitudes and Multiple Zeta Values, with their incarnation as Chen integrals on moduli spaces, as studied by Francis Brown, since the latter are a homotopical analog of de Rham Theory:

Quantum Amplitudes↔Integrals on Moduli Spaces.

The fact that maximally helicity violating (MHV) 3-point amplitudes reassemble the cross-ratios on the Riemann sphere (essentially the unique Lorentz invariant), with logarithm a hyperbolic metric, and that these “structure constants” determine in a recursive manner the n-point amplitudes, reassembling the antipode relation from Connes-Kreimer Hopf algebra approach to renormalization, is an indication that the quantum amplitudes are periods belonging to this framework: periods and motives².

3.3. Arithmetic Galois Theory and Anabelian Geometry

Specifically, the author’s reformulation of cohomology of cyclic groups as a discrete analog of de Rham cohomology [17] and the associated analog period isomorphism, will be related with the arithmetic Galois Theory [16], again as a discrete, purely algebraic toy-model of the said algebraic homology/homotopy group theory of Grothendieck. It will allow an elementary investigation of the main concepts defining periods and algebraic fundamental group, together with their conceptual relation to algebraic numbers and Galois groups.

4. Research Ramifications to TOEs and ADEX-Theory

The research will be placed in the larger context of the ADE-correspondence, since, for example, orbifolds of finite groups of rotations have crepant resolutions relevant in String Theory, while via Cartan-Killing Theory and exceptional Lie algebras, they relate to TOEs and VOAs.

The applications to ADE-correspondence, and beyond, e.g. toe ADEX-Theory [18], is an exciting R&D opportunity to perhaps finally understand what quark flavors and generations really are.

4.1. The Platonic Trinity

Arnold’s trinities [42] refer to Platonic symmetry groups $T\mathrm{,}O\mathrm{,}I$, related to exceptional Lie algebras $E\mathrm{6,}E\mathrm{7,}E8$ via the double of the first as Weyl groups. It also includes their invariant polynomials, and the Hopf bundles, but without reference to Klein quartic and the Galois groups $PS{L}_2\left(F_p\right)\mathrm{,}p=\mathrm{5,7,11}$.

What is remarkable (on top of other things), is that these “exceptional” $PS{L}^{\prime }s$ are cyclotomic fibrations over the Platonic groups of symmetry (TOI) of the Platonic tessellations of the Riemann sphere, as if they are finite qubit/Hopf bundles (see Galois’ last letter [43]):

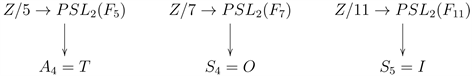
Remark 4.1. These seem to be related to the genus 2 (Fermat surface), 3 (Klein quartic), as described in [37] (What about $p=11$ ?).

Remark 4.2. The comments from §2.3.1 extend to this “coincidence”: is a locally finite model of the Universe, based on finite qubits, “The Way” to “quantize everything!?” …justifying even the fundamental “postulates”, e.g. quantization of angular momentum!

On the other hand, how do they relate to the higher genus Platonic tessellations via Belyi ramified covers, e.g. Klein’s quartic as a Hurwitz surface?³.

4.2. Role of the Exceptional Lie Algebra

Note that the role played by the exceptional Lie algebra, in this Finite Qubit Model (or Finite String Theory model) is not that of containing the SM gauge groups $U\left(1\right)\times SU{\left(2\right)}^L\times SU\left(3\right)$, since that would not be a true unification of interactions, and would not lead to a deeper understanding of masses of elementary particles etc., but rather as a kind of “loop groups” of paths due to multiple reflections in the virtual Weyl mirrors, as if the baryons (modeled by these rank 3 root systems) are some kind of kaleidoscopic beam splitters [44] !

5. Conclusions

The main result of the author’s research on the presented topics is rather a network of conceptual connections relating the Theory of Periods, Anabelian Geometry and scattering amplitudes on the physics side, and leading to a more focused plan of study.

More specifically, the main thread in this line of reasoning is to study algebraic de Rham cohomology and algebraic fundamental groups together, in order to understand why Feynman integrals (or scattering amplitudes in general, independent on a particular method of computation), are related to “homological periods” (algebraic de Rham isomorphism) on one hand, but are related to Chen iterated integrals in the Number Theory side, which is a homotopical de Rham Theory, hence to be studied in the algebraic context of Anabelian geometry.

One useful strategy is to investigate the relation between the theory of algebraic numbers and that of periods, with a starting point Riemann surfaces having a Belyi map.

This leads to the rich area of graphs embedded on surfaces, i.e. Dessins D’Enfant, as a sort of generalization of a lattice embedded in a vector space, and Hodge structures controlling how Betti homology “sits” inside de Rham cohomology.

A study of the category of morphisms of Belyi maps, which capture both the ramification data, but also divisor data and homotopy groups (Anabelian Galois groups), could in principle help clarify the role of the “change of variables” Kontsevich-Zagier relation, beyond the torsor due to isomorphism equivalence.

The analogy with the theory of decomposition of primes, corresponding to the structure of the Galois group (inertia, decomposition and degree), supports the belief that such a study could yield new results and a better understanding of the structure of the “absolute” ring of periods.

At the “elementary” level of Algebraic Number Theory, the representation point of view used to study the arithmetic Galois Theory (short exact sequences of Abelian groups and their $Au{t}_{Ab}\left(\right)$ symmetries), functorially corresponding to (algebraic) Galois Theory, can be thought of as an analog of covering spaces and deck transformations.

This provides another example of “Anabelian Geometry”, “a la Grothendieck”, together with, and corresponding to, the “main example” of algebraic fundamental groups, namely the Galois groups.

This homotopical theory aspects of Galois Theory in the non-commutative case will be studied elsewhere, together with the homological aspects, via the relation between the discrete de Rham cohomology [17] and algebraic de Rham cohomology of Grothendieck [3].

Specific problems, refining the general research suggested by the above considerations, will be addressed elsewhere:

1) The discrete analog of de Rham cohomology, and its connection with the Theory of Periods, via the algebraic de Rham cohomology.

2) Arithmetic Galois Theory and its functorial connection with classical Galois Theory of field extensions.

In the light of (1) above, (2) is expected to provide additional insight into the theory of periods and the period isomorphism, as homological analogues of algebraic numbers and associated Galois groups.

3) The connection with the Theory of Motives just claimed above, can be addressed by viewing Chow cycles as embedded cobordisms, allowing to establish an analogy at least, with TQFTs and providing support to the recent approach to motives by Y. Andre, via categories of representations of diagrams (analog to quiver representations, yet not necessarily finite). This direction is clearly consistent with the Physics side of the picture, starting to Feynman path integrals and Feynman diagrams, to quark line diagrams of the Standard Model, with its mathematical counterpart, Turaev ribbon calculus in modular categories.

At a more concrete level, applications to physics are proposed via the special case of Riemann Surfaces with Platonic tessellations, and the study of the role of the Hurwitz surfaces, i.e. those with maximal symmetry. For example, Klein quartic is instrumental in String Theory. It is explained how a detailed study could be a bridge between the Standard Model and String Theory, via a qubit model (Hopf bundle) interpretation.

There are of course rich connections with ADE-correspondence, Klein singu- larities and orbifolds, RS as crepant resolutions etc. [45], and also with TOEs (e.g. Lisi’s [46]) and ADEX Theory [18], emphasizing the roles of the exceptional Lie groups in fundamental physics, and perhaps more generally, the conceptual unity in Mathematical-Physics.

NOTES

¹This particular article of Karcher and Weber [37] seems to be a perfect source of info relevant for the present research goals.

²Physics is Mathematics discovered experimentally…

³…And further, with the Lie algebras, McKay and Gabriel reps theory, via ADE-correspondence.

Conflicts of Interest

The author declares no conflicts of interest regarding the publication of this paper.

References