The Mathematical Foundations of Elasticity and Electromagnetism Revisited ()
1. Introduction
At the beginning of the last century G. Lippmann and H. von Helmholtz, who knew each other, were both looking for the possibility to interpret thermostatic and electric phenomena by exhibiting a common macroscopic mechanical origin through a kind of variational calculus similar to the one used in analytical mechanics for getting Euler-Lagrange equations. As a byproduct, it is not possible to separate the Mach-Lippmann analogy from the Helmholtz analogy that we now recall.
In analytical mechanics, if
is the Lagrangian of a mechanical system, one easily gets the Hamiltonian
where t is time, q represents a certain number of dependent variables or generalized position, allowing to define the position of the various rigid bodies constituting the system (coordinates of center of gravity, relative angles, ...) and
is the derivative with respect to time or generalized speed. There are two ideas behind such a construction. The first is to introduce the energy as in the movement of a point of mass m with Cartesian coordinates (
vertical) or (
vertical) in the gravitational field
where
and thus
. The second is to take into account the well known Euler-Lagrange equations
implied by the variational condition
and to obtain therefore:
that is the conservation of energy along the trajectories whenever L does not contain t explicitly.
Similarly, in thermostatics, if F is the free energy of a system at absolute temperature T, we may obtain, in general, the internal energy U by the formula
. We explain the underlying difficulty in the case of a perfect gas with pressure P, volume V and entropy S for one mole. The first principle of thermostatics says that the sum of the exchange of work
and the exchange of heat
between the system and its surrounding is a total differential
. Now, the second principle of thermostatics says that
or equivalently that
is a total differential with absolute
temperature as integrating factor. Accordingly, we have
, a result giving U as a function of V and S. As V has a geometric meaning that S does not possess, engineers use to do a Legendre transformation by introducing
in order to have
where F is now a function of V and T that can be measured. It follows that
in this situation because
does not contain
. Of course, contrary to S, T can be measured though it does not seem to have a geometric meaning like V. In general, the 1-form
depends linearly on the differentials of all the state variables (
and
in our case) and there is no reason at all to have again
.To avoid such a situation, Helmholtz postulated the possibility for any system to choose “normal” state variables such that
should not appear in
. Therefore, if one could introduce V and T on an equal geometric footing, then
should already contain, in a built-in manner, not only the first and second principle but also the well defined possibility to recover U from F as before. In the case of continuum mechanics that we shall study later on, V must be replaced by the deformation tensor, as we shall see later on, which is a function of the first order derivatives of the actual (Euler) position x at time t with respect to the initial (Lagrange) position
at time
. Accordingly, the idea of Helmholtz has been to compare the relations
and
and to notice that they should become indeed similar if one could set
and
for a certain q. However, despite many attempts [1], nobody knows any variable q such that its derivative with respect to time should be the absolute temperature T of the system considered.
We now present the work done by Lippmann in a modern setting. The basic idea is to compare two kinds of conceptual experiments, namely a Carnot cycle for a steam engine working between the absolute temperatures
and
with
on one side, and a cycle of charge and discharge of a spherical condenser (say a soap buble) of radius r, moving in between two plates at constant electric potentials
and
with
on the other side ([2] [3] [4] [5]).
In the first case, let the system receive the heat
from the hot source and the heat
from the cold source through corresponding isothermal evolutions, while receiving the work
from the surroundings in a cycle completed by two adiabatic evolutions.
The vanishing of the cycle integral:
coming from the first principle of thermostatics leads to the relation
.
Then, the vanishing of the cycle integral coming from the second principle of thermostatics:
leads to the Clausius formula and the computation of the efficiency
:
Now, in the second case, things are quite more subtle. Recalling the formula
relating the charge q to the potential V of a condenser with
for a sphere of radius r, the electric energy should be:
Whenever C remains constant, the exchange of work done by the sources should be
because, by definition, sources are at constant potential, and we have
. However, the situation is completely different whenever C depends on r and we do not believe that Lippmann was very conscious about this fact. Let us suppose that the bubble receives the work
from the source at potential
for having its charge changing at constant potential
and similarly the work
from the source at constant potential
for having its charge changing at constant potential
, while receiving the (mechanical) work
from the surroundings for changing C in a cycle where the geometry of the system may vary (change of radius or distance). The problem is now to construct the cycle in order to be able to copy the procedure used for thermostatics. In the evolution at constant potential we have
, as already said, and therefore, comparing with
, the remaining evolution must be at constant charge, a situation happily realized in the experiment proposed by Lippmann, during the transport of the bubble from one plate to the other.
Now, taking into account the expression
already introduced and allowing C to vary (through r in our case), we have the formula:
if we express E as a function of C and q. In our case
and the relation
plays the role of the relation
existing for a perfect gas.
Copying the use of the first principle of thermostatics, the vanishing of the cycle integral provides:
Lippmann then notices that the conservation of entropy now becomes the conservation of charge and the vanishing of the cycle integral provides:
analogous to the Clausius formula with similar efficiency
, a result he called “Principe de conservation de l’électricité “ or “Second principe de la théorie des phénomènes électriques”.
One must notice the formula:
if we express E as a function of C and V. Also the analogue of the free energy should be
expressed as a function of C and V. Hence it is not evident, at first sight, to know whether the more “geometric” quantity is q or V.
Finally, the analogy between T and V in the corresponding “second principles” is clear and constitutes the Mach-Lippmann analogy. However, the reader may find strange that T, which is just defined up to a change of scale because of the existence of a reference absolute zero, should be put in correspondence with V which is defined up to an additive constant. In fact, the formula for the spherical condenser (Gauss theorem) is only true if the potential at infinity is chosen to be zero, as a zero charge on the sphere is perfectly detectable by counting the number of electrons on the surface. Accordingly, the two previous dimensionless ratios are perfectly well defined, independently of any unit chosen for T or V. However, such an analogy is perfectly coherent with the existence of thermocouples where the gradient of T is proportional to the gradient of V, that is we have for the electric field
and the latter difficulty entirely disappears.
We recall that the thermoelectric effect, that is the existence of an electric current circulating in two different metal threads A and B with soldered ends at different temperatures
and
, has been discovered in 1821 by the physicist Seebeck from the Netherlands. Also cutting one of the threads to set a condenser and integrating along the circuit, the difference of potential becomes:
Hence a thermocouple only works if
,
and tables of coefficients can be found in the literature. It is the French physicist Becquerel who got the idea in 1830 to use such a property for measuring temperature and Le Chatelier in 1905 who set up the platine thermocouple still used today. Meanwhile, J. Peltier proved that, when an electric current is passing in a thermocouple circuit with soldered joints at the same temperature, then one of the joints absorbs heat while the other produces heat. Also W. Thomson proved that an electric current passing in a piece of homogeneous conductor in thermal equilibrium gives a difference of potential at the ends whenever they are not at the same temperature.
We end this presentation of the Mach-Lippmann analogy with the main problem that it raises. From the special relativity of A. Einstein in 1905 [6] it is known that space cannot be separated from time and that one of the best examples is given by the relativistic formulation of EM. Indeed, instead of writing down separately the first set of Maxwell equations for the electric field
and the magnetic field
under their classical form, ne may introduce local coordinates
where c is the speed of light and consider the 2-form
with standard notations:
in order to obtain:
where
is the exterior derivative.
Similarly, introducing the electromagnetic potential
and the electric potential V in the 1-form
where
is the time component, we obtain:
though, surprisingly, V has been introduced in thermostatics. Hence, even if we may accept and understand an analogy between T and V, we cannot separate V from
in the 4-potential A and a good conceptual analogy should be between T and
.
The surprising fact is that almost nobody knows about the Mach-Lippmann analogy today but many persons are using it through finite element computations and thus any engineer working with finite elements knows that elasticity, heat and electromagnetism, though being quite different theories at first sight, are organized along the same scheme and cannot be separated because of the existence of the following couplings that we shall study with more details in the next Section.
• THERMOELASTICITY (Elasticity/Heat):
When a bar of metal is heated, its length is increasing and, conversely, its length is decreasing when it is cooled down. It is a perfectly reversible phenomenon.
• PIEZOELECTRICITY, PHOTOELASTICITY (Elasticity/Electromagnetism):
When a crystal is pinched between the two plates of a condenser, it produces a difference of potential between the plates and conversely, in a purely reversible way. Piezoelectric lighters are of common use in industry. Similarly, when a transparent homogeneous isotropic dielectric is deformed, piezoelectricity cannot appear but the index of refraction becomes different along the three orthogonal proper directions common to both the strain and stress tensors. Here we recall that a material is called “homogeneous” if a property does not depend on the point in the material and it is called “isotropic” if a property does not depend on the direction in the material. Accordingly, a light ray propagating along one of these directions may have its electric field decomposed along the two others and the two components propagate with different speeds. Hence, after crossing the material, they recompose with production of an interference pattern, a fact leading to optical birefringence. Such a property has been used in order to get information on the stress inside the material, say a bridge or a building, by using reduced transparent plastic models. This phenomenon was discovered by Brewster in 1815 but the phenomenological law that we shall prove in the next section, was proposed independently by F.E. Neumann and J.C. Maxwell in 1830. Until recently one used to rely on the mathematical formulation proposed by Pöckels in 1889 but modern versions can easily be found today in the engineering literature.
• THERMOELECTRICITY (Heat/Electromagnetism):
We have already spoken about this coupling which, nevertheless, can only be understood today within the framework of the phenomenological Onsager relations for irreversible phenomena. If we want to make the Fourier law
between heat flux and gradient of temperature more precise, we may suppose that the heat conductivity
also depends on the magnetic field and we may obtain “a priori” the additional term
. In a homogeneous medium, one has
when
is the space Euclidean metric and we have
,
with
, that is
. We have thus been able to recover the Righi-Leduc effect in a purely macroscopic way.
Hence, as a very restrictive conclusion, we discover that the Mach-Lippmann analogy must be at least set up in a clear picture of the analogy existing between elasticity, heat and electromagnetism that must also be coherent with the above couplings.
2. Elasticity versus Electromagnetism
The rough idea is to make the constitutive law of an homogeneous isotropic dielectric
where
is the electric induction and
,
being the vacuum value (universal constant) of the dielectric constant, such that the dielectric susceptibility
now depends on the deformation (or stress) tensor in each direction. Keeping the constitutive relation
where
is the magnetic induction and
the vacuum value (universal constant) of the magnetic constant, as we have no magnetic polarization in the medium, it is well known that
and thus
where n is the index of refraction such that
, a result leading to the Maxwell-Neumann formula
that we shall demonstrate and apply to the study of a specific beam. In this formula
are the two eigenvalues of the symmetric stress tensor along directions orthogonal to the ray, k is a relative integer fixing the lines of interference,
is the wave length, e is the thickness of the transparent beam and C is the photoelastic constant of the material.
With more details, the infinitesimal deformation tensor of elasticity theory is equal to half of the Lie derivative
of the euclidean metric
with respect to the displacement vector
. Hence, a general quadratic lagrangian may contain, apart from its standard purely elastic or electrical parts well known by engineers in finite element computations, a coupling part
where
is the electric field. The corresponding induction
becomes:
and is therefore modified by an electric polarization
, brought by the deformation of the medium. In all these formulas and in the forthcoming ones the indices are raised or lowered by means of the euclidean metric. If this medium is homogeneous, the components of the 3-tensor c are constants and the corresponding coupling, called piezoelectricity, is only existing if the medium is non-isoptropic (like a crystal), because an isotropic 3-tensor vanishes identically.
In the case of an homogeneous isotropic medium (like a transparent plastic), one must push the coupling part to become cubic by adding
with
from Curie’s law. The corresponding coupling, called photoelasticity, has been discovered by T. J. Seebeck in 1813 and D. Brewster in 1815. With
, the new electric induction is:
As
is a symmetric tensor, we may choose an orthogonal frame at each point of the medium in such a way that the deformation tensor becomes diagonal with
where the third direction is orthogonal to the elastic plate. We get:
for
without implicit summation and there is a change of the dielectric constant
along each proper direction in the medium, corresponding to a change
of the refraction index. As there is no magnetic property of the medium and
, we obtain in first approximation:
where
is the magnetic constant of vacuum, c is the speed of light in vacuum and n is the refraction index. The speed of light in the medium becomes
and therefore depends on the polarization of the beam. As the light is crossing the plate of thickness e put between two polarized filters at right angle, the entering monochromatic beam of light may be decomposed along the two proper directions into two separate beams recovering together after crossing with a time delay equal to:
providing interferences and we find back the Maxwell phenomenological law of 1850:
where
is the stress tensor, k is an integer,
is the wave length of the light used and C is the photoelastic constant of the medium ivolved in the experience.
Looking at the picture, let F be the vertical downwards force acting on the upper left side of the beam like on the picture, at a distance D from the center of the vertical beam on the right. We may consider this vertical beam as a dense sheaf of juxtaposed thin beams with young modulus E. Choosing orthogonal axes (Oxyz) such that Ox is horizontal towards the right with origin O in the geometric center of the vertical beam on the right which has a thickness
and a width of 2b with the vertical axis Oy passing in the center of the beam. If F should be applied along Oy, according to Hooke’s law there should be a vertical compression of the beam providing a deformation roughly equal to
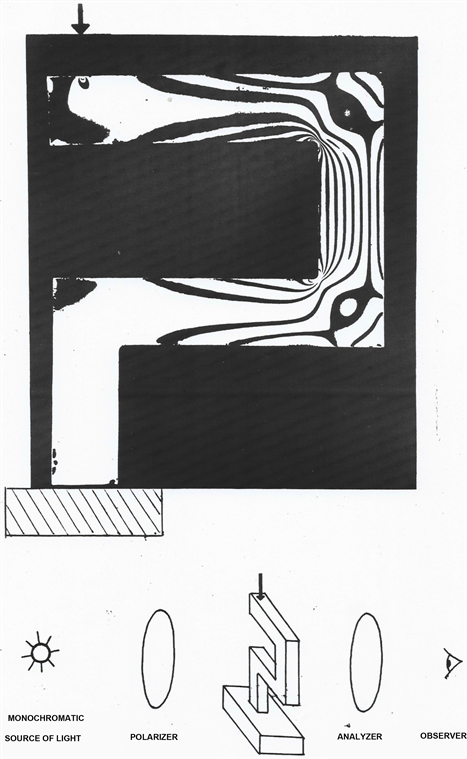
and a (negative because compression) stress
. However, F is applied at a distance D of the axis Oy and gives a couple
which should be, by itself, bringing the half right part of the beam (
) in extension while the half left part (
) is in compression. Using a classical assumption usually done on beams we may suppose that the horizontal plane sections orthogonal to the central axis Oy of the beam stay plane surfaces turning counterclockwise by a small angle
that we shall determine by integration on all the small thin beams of the bunch. The stress
acting on the surface
is producing a small force
. However, a fiber at distance
from the axis has a length increased by
and there is a resulting deformation
such that
on each thin constitutive fiber. The resulting (direct sense) couple produced is equal to
in such a way that we have the equilibrium equation for couples:
We obtain therefore
with
whenever
(extension). Using the correct negative sign for the stress
, we finally obtain
in such a way that
when
and
when
, a result not evident at first sight. In addition, it is clear by symmetry that
are proper directions and that
because no force is acting on the faces of the beam. We obtain therefore the very simple Maxwell law
. Accordingly, the (almost!) central black line corresponds to
and has abcissa
. Finally, the distance d between two lines is such that k is modified by 1, that is
, allows to determine the photoelastic constant of the material.
The study of the upper horizontal part of the beam is more delicate. With axis Oy in the middle section, starting under the force F and axix Ox upward, we have
to compensate the couple Fy but now we have a shear stress
upward to compensate F which is downward. The characteristic polynomial is
and thus
cannot vanish. Therefore the line “
” cannot exist. As for the lines “
”, we must have after substitution
and we need to have thus
or equivalently
, a result simply leading to the hyperbola
, a property that can be checked on the picture but cannot be even imagined.
We have thus explained, in a perfectly coherent way with the picture, why the interference lines are parallel and equidistant from each other in the right vertical part of the beam, on both sides of an (almost) central line which, surprisingly, stops at the upper and lower corner, even though, by continuity, we could imagine that it could be followed in the upper and lower horizontal parts of the beam. Also, we understand now the reason for which the lines in these parts of the beam look like symmetric hyperbolas.
This result proves, without any doubt for anybody doing this experiment, that the deformation
and the electromagnetic field
, using standard notations in the space-time formulation of electromagnetism, must be on equal footing in a lagrangian formalism. However, as
is in the Janet sequence based on the work of E. Vessiot in 1903 (Compare [7] to [8] [9] [10] [11]) and
cannot appear at this level as we shall see, the main purpose of this paper is to prove that another differential sequence must be used, namely the Spencer sequence. The idea has been found totally independently, by the brothers E. and F. Cosserat in 1909 ([12]) for revisting elasticity theory and by H. Weyl in 1916 ([13]) for revisiting electromagnetism by using the conformal group of space time, but the first ones were only dealing with the translations and rotations while the second was only dealing with the dilatation and the non-linear elations of this group, with no real progress during the last hundred years.
Extending the space
or
to space-time
as before, the speed is now extended from
to
along the derivative with respect to time, with
, while the motion
is extended to
in order to compare “slices” of space at the same “time”. Accordingly, the deformation tensor
, which is
dimensionless, is extended by
while the symmetric stress tensor
becomes
(Euler theorem) and is extended by setting
,
where
is the mass per unit volume. Dealing with the rest-frame and using the (small) dilatation relation
in which
is the value of
in the initial position where the body is supposed to be homogeneous, isotropic and unstressed, that is,
is supposed to be a constant. The Hooke law is now extended by setting:
in a way compatible with the conservation of mass and we suddenly discover that there is no conceptual difference between the Lamé constants
(do not confuse the notations) of elasticity and the magnetic constant
on one side (space) or the mass per unit volume
and the dielectric constant
(time) on the other side, all these coupling constants being measured in the reference state in which the body (like vacuum) is homogeneous and isotropic (the index “zero” is omitted for simplicity). This result is perfectly coherent “a posteriori” with the analogy existing between the well known formulas for the speed
of transverse elastic waves, the speed
of longitudinal elastic waves or the speed v of light waves propagating in a homogeneous isotropic medium, as we have indeed ([14]):
We now understand that couplings are in fact more general constitutive laws taking into account the tensorial nature of the various terms involved through the Curie principle.
3. General Relativity versus Gauge Theory
Let A be a unitary ring, that is
and even an integral domain (
or
) with field of fractions
. However, we shall not always assume that A is commutative, that is ab may be different from ba in general for
. We say that
is a left module over A if
or a right module
over B if the operation of B on M is
. If M is a left module over A and a right module over B with
, then we shall say that
is a bimodule. Of course,
is a bimodule over itself. We define the torsion submodule
and M is a torsion module if
or a torsion-free module if
. We denote by
the set of morphisms
such that
and set
. We shall only consider finitely generated modules, recalling that a sequence of modules and maps is exact if the kernel of any map is equal to the image of the map preceding it ([15] - [20] are good references for homological algebra).
When A is commutative,
is again an A-module for the law
as we have
. In the non-commutative case, things are more complicate and, given
and
, then
becomes a right module over B for the law
.
DEFINITION 3.1: A module F is said to be free if it is isomorphic to a (finite) power of A called the rank of F over A and denoted by
while the rank
of a module M is the rank of a maximum free submodule
. It follows from this definition that M/F is a torsion module. In the sequel we shall only consider finitely presented modules, namely finitely generated modules defined by exact sequences of the type
where
and
are free modules of finite ranks
and
often denoted by m and p in examples. A module P is called projective if there exists a free module F and another (projective) module Q such that
.
PROPOSITION 3.2: For any short exact sequence
, we have the important relation
, even in the non-commutative case. As a byproduct, if M admits a finite length free resolution
, we may define the Euler-Poincaré characteristic
.
We now turn to the operator framework with modules over the ring
of differential operators with coefficients in a differential field K with n commuting derivations
, also called D-modules. Then D is a differential bimodule over itself ([18] [19] [21] [22] [23] [24] are good references for differential homological algebra while [8] [9] [10] [11] [18] [19] [25] are good references for the formal theory of systems of partial differential equations).
DEFINITION 3.3: If a differential operator
is given, a direct problem is to find generating compatibility conditions (CC) as an operator
such that
. Conversely, given
, the inverse problem will be to look for
such that
generates the CC of
and we shall say that
is parametrized by
if such an operator
is existing.
Introducing the morphism
such that
and defining the differential module N from
exactly like we defined the differential module M from
, we finally notice that any operator is the adjoint of a certain operator because
and we get ([18] [19] [26] [27] [28] [29]):
THEOREM 3.4: (double differential duality test) In order to check whether M is torsion-free or not, that is to find out a parametrization if
, the test has 5 steps which are drawn in the following diagram where
generates the CC of
and
generates the CC of
:
COROLLARY 3.5: In the differential module framework, if
is a finite free presentation of
with
, then we may obtain an exact sequence
of free differential modules where
is the parametrizing operator. However, there may exist other parametrizations
called minimal parametrizations such that
is a torsion module and we have thus
.
These results have been used in control theory and it is now known that a control system is controllable if and only if it is parametrizable (See [18] [19] [30] [31] for more details). As a byproduct, and though it is still not acknowledged by engineers, controllability is a “built in” property that does not depend at all on the choice of the inputs and outputs among the control variables.
Keeping the same “operational” notations for simplicity, we may state ([18], p 638-650):
DEFINITION 3.6: We say that
admits a (generalized) lift
if
. The differential module determined by
is projective if and only if
admits a lift.
The following results have never been used for applications:
LEMMA 3.7: If
admits a lift, then
also admits a lift.
PROPOSITION 3.8: If
parametrizes
and admits a lift
, then
admits a lift
and we have the striking Bezout identity
. Accordingly, the corresponding differential sequence, which is formally exact by definition, is also locally exact.
COROLLARY 3.9: If
generates the CC of
and both operators admit lifts, then
generates the CC of
.
EXAMPLE 3.10: With
,
,
,
,
,
and
we shall prove that
is torsion-free but not projective when
and projective but not free when
, for example when
. Multiplying
by a test function
and integrating by parts formally the equation
, we get the operator
in the form:
•
: We get the only generating CC
and
is not injective. There is therefore no lift and thus no splitting. Multilying by a test function
and integrating by parts, we obtain the parametrization
in the form
which is not injective. The corresponding sequence
with differential modules and its formal adjoint are both formally exact.
•
: The situation is now totally different. In order to prove this, if we suppose that
, we get the lift
with adjoint
providing a lift
for
. Substituting, we obtain two second-order CC
and
satisfying the only CC
. Multiplying these two CC by the test functions
and
and integrating by parts, we finally obtain the involutive parametrizing operator
in the form:
and “a” minimum involutive parametrization (but there can be others!):
We get the long formally and locally exact differential sequence
and invite the reader to find a lift for the central operator as an exercise.
EXAMPLE 3.11: When
, the div operator can be parametrized by the curl operator which can be itself parametrized by the grad operator. However, using
, we may obtain the new minimal parametrization
,
,
which cannot be again parametrized ([29] [32]).
EXAMPLE 3.12: Parametrization of the Cauchy stress equations.
We shall consider the cases
but the case n arbitrary could be treated as well.
•
: The stress equations become
,
. Their second order parametrization
,
,
has been provided by George Biddell Airy in 1863 ([33]) and we shall thus denote by
the corresponding operator. We get the linear second order system with formal notations:
which is involutive with one equation of class 2, 2 equations of class 1 and it is easy to check that the 2 corresponding first order CC is just the stress equations. Now, multiplying the Cauchy stress equations respectively by test functions
and
, then integrating by parts, we discover that (up to sign and a factor 2) the Cauchy operator is the formal adjoint of the Killing operator defined by
, introducing the standard Lie derivative of the (non-degenerate) euclidean metric
with respect to
and using the fact that we have
because we have supposed that
and we shall say, with a slight abuse of language, that
. In order to apply the above parametrization test, we have to look for the CC
of
. In arbitrary dimension n, we may introduce the Riemann tensor
with
components of a general metric
such that
and linearize it over a given non-degenerate constant metric or, more generally, over a metric with constant Riemaniann curvature, in order to obtain the second order Riemann operator
. When
and
is the euclidean metric, we get a single component that can be chosen to be the scalar curvature
. Multiplying by a test function
and integrating by parts, we obtain
and notice that:
There is no relation at all between the Airy stress function
and the deformation
of the metric
.
•
: Things become quite more delicate when we try to parametrize the 3 PD equations:
A direct computational approach has been provided by Eugenio Beltrami in 1892 ([34]), James Clerk Maxwell in 1870 ([35]) and Giacinto Morera in 1892 ([36]) by introducing 6 stress functions
in the Beltrami parametrization described by the following Beltrami operator:
It is involutive with 3 equations of class 3, 3 equations of class 2 and no equation of class 1. The 3 CC is describing the stress equations which admit therefore a parametrization, but without any geometric framework, in particular without any possibility to imagine that the above second order operator is nothing else but the formal adjoint of the Riemann operator, namely the (linearized) Riemann tensor with
independent components when
[8] [9] [10] [11]. We may rewrite the Beltrami parametrization of the Cauchy stress equations as follows, after exchanging the third row with the fourth row and using formal notations:
as an identity where 0 on the right denotes the zero operator. However, the standard implicit summation used in continuum mechanics (See [36] for more details) is, when
:
because the stress tensor density
is supposed to be symmetric in continuum mechanics. Integrating by parts in order to construct the adjoint operator, we get the striking identification:
between the (linearized ) Riemann tensor and the Beltrami parametrization.
As we already said, the brothers E. and F. Cosserat proved in 1909 that the assumption
may be too strong because it only takes into account density of forces and ignores density of couples, and the Cauchy stress equations must be replaced by the so-called Cosserat couple-stress equations ([9] [10] [12] [37] [38]). In any case, taking into account the factor 2 involved by multiplying the second, third and fifth row by 2, we get the new
matrix with rank 3:
This is a symmetric matrix and the corresponding second order operator with constant coefficients is thus self-adjoint.
Surprisingly, the Maxwell parametrization is obtained by keeping only
,
,
while setting
and using only the columns
as follows:
and we let the reader check the corresponding Cauchy equations.
: It is only now that we are able to explain the relation of this striking result with Einstein equations but the reader must already understand that, if we need to revisit in such a deep way the mathematical foundations of elasticity theory, we also need to revisit in a similar way the mathematical foundations of EM and GR as in ([28] [32] [36] [39] [40] [41] [42]). To begin with, let us introduce the Ricci operator
with 4 terms and the Einstein operator
with 6 terms where the trace of
is just
. Surprisingly, the Einstein operator is self adjoint while the Ricci operator is not and “Einstein equations are just a way to parametrize the Cauchy stress equations” because of the well known contraction of the Bianchi identities ([29] [31] [32] [44]). Now, Theorem 3.4 proves that the Einstein operator cannot be parametrized ([31] [40]) and that each component of the Weyl tensor is a torsion element killed by the Dalembertian ([18] [32] [44]). We now prove that only the use of differential homological algebra, a mixture of differential geometry (differential sequences, formal adjoint) and homological algebra (module theory, double duality, extension modules) totally unknown by physicists, is able to explain why the Einstein operator (with 6 terms) defined above is useless as it can be replaced by the Ricci operator (with 4 terms) in the search for gravitational waves equations. Indeed, denoting by
a perturbation of the non-degenerate metric
, it is well known (See [8] [10] and [47] for more details) that the linearization of the Ricci tensor
over the Minkowski metric, considered as a second order operator
, may be written with four terms as ([32] [43]):
Multiplying by test functions
and integrating by parts on space-time, we obtain the following four terms describing the so-called gravitational waves equations:
where
is the standard Dalembertian. Accordingly, we have:
The basic idea used in GR has been to simplify these equations by adding the differential constraints
in order to find only
, exactly like in the Lorenz condition for EM. It follows that the Cauchy = ad(Killing) operator is parametrized by
and, not only the Einstein operator is useless as it must be replaced by
but also this result shows that the Cauchy operator has nothing to do with the Bianchi operator. Finally, as our comment on the Airy operator when
is still valid,
has nothing to do with
and we may say ([32]):
These purely mathematical results question the origin and existence of gravitational waves.
It remains to prove that, in this new framework, the Ricci tensor only depends on the symbol
of the first prolongation
of the conformal Killing system
with symbol
defined by the equations
not depending on any conformal factor. In the next general commutative diagram covering both situations while taking into account that the PD equations of both the classical and conformal Killing systems are homogeneous, the Spencer map
is induced by minus the Spencer operator and all the sequences are exact but perhaps the left column with
-cohomology
at
(See [8] [9] [10] [11] or [25] for more details):
We have the following fiber dimensions for the classical Killing case and arbitrary dimension n:
allowing to recover the number of components of the Riemann tensor... without indices ! with
too.
We obtain at once from a snake-type chase the isomorphism
and provide a new simple proof of the following important result (Compare to [10] [11] [32] [40] [41] and the Remark below):
THEOREM 3.13: Introducing the
-cohomologies
at
and
at
while taking into account that
, we have the short exact sequences:
Proof: The first result can be deduced from a delicate unusual chase in the following commutative diagram where only the rows and the right column are short exact sequences. The first step is made by a diagonal snake-type chase for defining the left morphism and we let the reader check that it is a monomorphism. The right morphism is described by the inclusion
induced by the inclusion
by showing that any element of
is a sum of an element in
plus the image by
of an element in
for the right epimorphism (exercise).
with fiber dimensions when
:
Using the previous diagram, we obtain the isomorphisms
and
. We have thus the splitting sequence
providing a totally unusual interpretation of the successive Ricci, Riemann and Weyl tensors. It follows that
whenever
and the Weyl-type operator is of order 3 when
but of order 2 for
. Similar results could be obtained for the Bianchi-type operator ... with much more work!
Q.E.D
REMARK 3.14: Using the contraction
, namely
, in order to describe the cokernel of the left vertical monomorphism, we obtain the following commutative and exact diagram which is only depending on the first order jets of T:
Prolonging twice to the jets of order 3 of T, we obtain the commutative and exact diagram:
providing the same short exact sequence as in the Theorem but without any possibility to establish a link between
and a 1-form with value in the bundle
of elations.
EXAMPLE 3.15: Electromagnetism.
Passing now to electromagnetism and the original Gauge Theory (GT) which is still, up to now, the only known way to establish a link between EM and group theory, the first idea is to introduce the nonlinear gauge sequence:
where X is a manifold, G is a Lie group with identity e not acting on X,
a map identified with a section of the trivial bundle
over X and
is the pull-back over X by the tangent mapping
of a basis of left invariant 1-forms on G. Also,
by introducing the bracket on the Lie algebra
and the pull-back of the Maurer-Cartan (MC) equations on G is the so-called Cartan curvature 2-form with value in
. Choosing a close to e, that is
with
and linearizing as usual, we obtain the linear operator
leading to the linear gauge sequence:
which is the tensor product by
of the Poincaré sequence for the exterior derivative d. In 1954, at the birth of GT, the above notations were coming from electromagnetism with EM potential
and EM field
in the relativistic Maxwell theory. Accordingly,
(unit circle in the complex plane)
was the only possibility existing before 1970 to get a pure 1-form A (EM potential) and a pure 2-form F (EM field) when G is abelian. However, this result is not coherent at all with elasticity theory as we saw and, a fortiori, with the analytical mechanics of rigid bodies where the Lagrangian is a quadratic expression of such 1-forms when
and
(Compare to [45] and [46]).
Before going ahead, let us prove that there may be mainly two types of differential sequences, the Janet sequence introduced by M. Janet in 1970 ([8] [11] [47]) for the dealing with successive compatibility conditions (CC), and a quite different sequence called Spencer sequence introduced by D. C. Spencer in 1970 ([8] [25] for the linear framework, [9] [48] for the non-linear framework) with totally different operators. For this, if E is a vector bundle over the base X, we shall introduce the q-jet bundle
over X with (local) sections
transforming like the (local) sections
. When
is the tangent bundle of X, the Spencer operator
and its extension
defined by
with
as we saw for the inverse system, allow comparing these sections by considering the differences
and so on. When
is a nondegenerate metric with Christoffel symbols
and Levi-Civita isomorphism
, we consider the second order involutive system
defined by considering the first order Killing system
, adding its first prolongation
and using
instead of
. Looking for the first order generating compatibility conditions (CC)
of the corresponding second order operator
just described, we may then look for the generating CC
of
and so on, exactly like in the differential sequence made successively by the Killing, Riemann, Bianchi, ... operators. We may proceed similarly for the injective operator
, finding successively
and
induced by D. When
and
is the Euclide metric, we have a Lie group of isometries with the 3 infinitesimal generators
. If we now consider the Weyl group defined by
with
and
, we have to add the only dilatation
. Collecting the results and exhibiting the induced kernel upper differential sequence, we get the following commutative fundamental diagram I where the upper down arrows are monomorphisms while the lower down arrows are epimorphisms
:
It follows that “Spencer and Janet play at see-saw”, the dimension of each Janet bundle being decreased by the same amount as the dimension of the corresponding Spencer bundle is increased, this number being the number of additional parameters multiplied by
because:
The linear Spencer Sequence is locally isomorphic to the linear gauge sequence for Lie groups, with the main difference that the group is now acting on the manifold, contrary to the previous situation.
More generally, whenever
is an involutive system of order q on E, we may define the Janet bundles
for
by the short exact sequences ([8]):
We may pick up a section of
, lift it up to a section of
that we may lift up to a section of
and apply D in order to get a section of
that we may project onto a section of
in order to construct an operator
generating the CC of
in the canonical linear Janet sequence:
If we have two involutive systems
, the Janet sequence for
projects onto the Janet sequence for
and we may define inductively canonical epimorphisms
for
by comparing the previous sequences for
and
, as we already saw.
We can also define the Spencer bundles
for
by the short exact sequences ([8]):
We may pick up a section of
, lift it to a section of
, lift it up to a section of
and apply D in order to construct a section of
that we may project to
in order to construct an operator
generating the CC of
in the canonical linear Spencer sequence which is another completely different resolution of the set
of (formal) solutions of
:
However, if we have two systems as above, the Spencer sequence for
is now contained into the Spencer sequence for
and we may construct inductively canonical monomorphisms
for
by comparing the previous sequences for
and
.
When dealing with applications, we have set
and considered systems of finite type Lie equations determined by Lie groups of transformations. In this specific case, it can be proved that the Janet and Spencer sequences are formally exact, both with their respective adjoint sequences ([11] [28] [32] [36] [38]), namely
generates the CC of
while
generates the CC of
. We have obtained in particular
when comparing the classical and conformal Killing systems, but these bundles have never been used in physics. Therefore, instead of the classical Killing system
defined by
and
or the conformal Killing system
defined by
and
, we may introduce the intermediate differential system
defined by
with
and
, for the Weyl group obtained by adding the only dilatation with infinitesimal generator
to the Poincaré group, exactly like we already did when
. We have
but the strict inclusions
and we discover exactly the group scheme used through this paper, both with the need to shift by one step to the left the physical interpretation of the various differential sequences used. Indeed, as
because
, the first Spencer operator
is induced by the usual Spencer operator
and thus projects by cokernel onto the induced operator
. Composing with
, it projects therefore onto
as in EM and so on by using the fact that
and d are both involutive, or the composition of epimorphisms:
The main result we have obtained is thus to be able to increase the order and dimension of the underlying jet bundles and groups, proving therefore that any 1-form with value in the second order jets
(elations) of the conformal Killing system (conformal group) can be decomposed uniquely into the direct sum
where R is a section of the Ricci bundle
and the EM field F is a section of
(Compare to [49]).
Lippmann got the Nobel prize in 1908 for the discovery of color photography. Only one year later, in 1909, the brothers E. and F. Cosserat wrote their “Théorie des corps déformables” ([12]) and it is in this book that the previous analogies are quoted for the first time. Between 1895 and 1910, the two brothers published together a series of Notes in the “Comptes Rendus de l’Académie des Sciences de Paris’’ and long Notes in famous textbooks or treatises on the mathematical foundations of elasticity theory (Compare to [50]). In particular, they proved that one can exhibit all the concepts and formulas to be found in elasticity theory (deformation/strain, compatibility conditions, stress, stress equations, constitutive relations, ...) just by knowing the group of rigid motions of ordinary 3-dimensional space with 3 translations and 3 rotations [10] [51].
It is rather astonishing that all the formulas that can be found in the book written by E. and F. Cosserat in 1909 are nothing else but the formal adjoint of the Spencer operator for the Killing equations. More precisely, a section
of the first prolongation
of the system
of Killing equations is a section of the 2-jet bundle
of the tangent bundle
, namely a set of functions
, transforming like the derivatives
of a vector field
but also satisfying the linear equations:
where
is the euclidean metric. Multiplying by test fuctions
and
respectively the zero and first order components of the image
of the corresponding Spencer operator D, then integrating by part while moving up and down the dumb indices by means of the metric, we successively obtain:
with evident notations for the Einstein summations involved (Compare to [12] p 137 and 167).
Keeping in mind that, in space-time, there are 4 translations
and 6 rotations
(3 space rotations + 3 Lorentz transformations), we recover all the
variations that can be found in the engineering calculus leading to finite element computations (MODULEF library for example). In addition, we have proved in many books ([10] [11] [18] [28]) and papers ([39] [41] [42]) that the conformal group of space-time is the biggest group of invariance of the Minkowski constitutive laws of EM in vacuum while both sets of Maxwell equations are invariant by any diffeomorphism (care!). In particular, considering the space-time dilatation
for
with infinitesimal generator
, a transformation which has no intuitive meaning, and gauging the connected compoment
of the identity with the distinguished identity 1, that is to say transforming the group parameters into functions, just explains why there must be a zero lower bound in the measure of absolute temperature, both with a distinguished value and invariance under
.
This result clarifies the Helmholtz analogy within jet theory. Indeed, if T is identified with the inverse of a first jet of dilatation, then T behaves like the derivative of a function without being such a proper derivative, and we find again exactly the definition of a jet coordinate. Such a result should lead in the future to revisit the foundations of thermostatics and thermodynamics ([42]).
The additional 4 transformations, called elations, are highly nonlinear and we understand that, contrary to E. and F. Cosserat who succeeded in dealing with the linear transformations, H. Weyl did not succeed in relating electromagnetism with the second order jets of the conformal group in ([13]), though the idea was a genious one, simply because he could not use in 1920 a mathematical tool created in 1970 ([25] [47]) but only effective in 1983 ([9] [10] [11] [41] [42]).
The reader may now understand that such a geometric unification was indeed the dream of the brothers E. and F. Cosserat who refer many times explicitly to the work of Mach and Lippmann ([12], p 147, 211). More precisely, using now the conformal Killing equations, we have:
where
is an arbitrary function and
is an arbitrary 1-form, we get
and
for
[8] [9] [10] [11]. Accordingly, the zero, first and second order components (field) of the image
of the Spencer operator D are:
and we can recover
. Identifying the speed with a (gauged) Lorentz rotation, that is to say setting
as a constraint ([12]), we can therefore measure both
for
(care to the sign!) and
, thus
by substraction, where
is the acceleration, and thus
in first approximation ([52], p. 922). Also, the formula
exactly describes the results of [13] by means of the Spencer operator and explains why the EM field is on equal footing with deformation and gradient of temperature, contrary to its status in gauge theory.
Roughly speaking, E. and F. Cosserat were only using the zero and first order components of the image of the Spencer operator while H. Weyl was only using the first and second order components (See [38] for more comments and [9] [10] [11] [39] [42] for a nonlinear version).
4. Conclusions
Recapitulating all the results previously obtained, we may finally say (See the end of [39]):
• “Beyond the mirror” of the classical approach to apparently well known and established theories, there is a totally new interpretation of these theories and the corresponding field/matter couplings by means of the Spencer sequence for the conformal Killing operator.
• The purely mathematical results of Section 3 perfectly agree with the origin and existence of elastic and electromagnetic waves but question the origin and existence of gravitational waves because the parametrization of the Cauchy operator can be simply done by the adjoint of the Ricci operator without any reference to the Einstein or even Bianchi operators. We believe that such a confusion mainly came from the fact that it had never been noticed that the Einstein operator was self-adjoint.
• They prove that the concept of “field” in a physical theory must not be related with the concept of “curvature” because it is a 1-form with value in a Lie algebroid (first Spencer bundle) and not a 2 form with value in a Lie algebra (second Spencer bundle). The “shift by one step” in the physical interpretation of a differential sequence is thus the main feature of this new mathematical framework.
• They also prove that gravitation and electromagnetism have a common conformal origin. In particular, electromagnetism has only to do with the conformal group of space-time and not with
as it is still believed today in Gauge Theory.
Main Mathematical Notations
X manifold with tangent, cotangent, symmetric, skewsymmetric bundles
q-jet bundle of the vector bundle E over X with
involutive system of order q on E with symbol
Janet bundles
generic Spencer bundles
Spencer bundles
exact sequences with
induced by
and
Spencer sequence with
induced by
Janet sequence of successive compatibility conditions (CC)
G Lie group with identity e and Lie algebra
with bracket []
Maurer-Cartan nonlinear gauge sequence
pull back of
and Cartan curvature.