Quenching Phenomena Due to a Concentrated Nonlinear Source in an Infinitely Long Cylinder

Patcharin Tragoonsirisak Marion

Department of Mathematics and Computer Science, Fort Valley State University, Fort Valley, GA, USA.

DOI: 10.4236/jamp.2019.79138                

Abstract

This article studies a semilinear parabolic first initial-boundary value problem with a concentrated nonlinear source in an infinitely long cylinder. We study the effects of the strength of the source on quenching. Criteria for global existence of the solution and for quenching are investigated.

Keywords

Quenching, Concentrated Nonlinear Source, Infinitely Long Cylinder

1. Introduction

The quenching phenomena have been studied since 1975 [1]. The quenching models have many applications in science and engineering. For example, the models may include combustion, ignition, thermal explosion and damage of material. In some situation, the model involves a concentrated source, such as in a chemical reaction process due to the effect of a catalyst, or in the ignition of a combustible medium through the use of either a heated wire or a pair of small electrodes to supply a large amount of energy to a very confined area [2]. In 2006, the quenching problem with a concentrated source has been posted correctly in a multi-dimensional bounded domain by Chan [3]. In this paper, we study the quenching problem with a concentrated nonlinear source in the unbounded domain, the infinitely long cylinder.

Let R and b be positive real numbers such that b < R, D be a two-dimensional ball centered at the origin with a radius R or $D=\left\{x\in {ℝ}^2:\left|x\right|<R\right\}$, $\partial D=\left\{x\in {ℝ}^2:\left|x\right|=R\right\}$, B be a two-dimensional ball centered at the origin with a radius b or $B=\left\{x\in {ℝ}^2:\left|x\right|<b\right\}$, and $\partial B=\left\{x\in {ℝ}^2:\left|x\right|=b\right\}$. We also let $\Omega$ and ω be the infinitely long cylinders centered at the origin with the radii R and b respectively. Namely, $\Omega =D\times \left(-\infty ,\infty \right)$, $\partial \Omega =\partial D\times \left(-\infty ,\infty \right)$, $\omega =B\times \left(-\infty ,\infty \right)$, and $\partial \omega =\partial B\times \left(-\infty ,\infty \right)$. For $x\in {ℝ}^3$, let υ(x) denote the unit outward normal at $x\in \partial \omega$, and ${\chi }_{\omega }\left(x\right)$ be the characteristic function which is 1 for $x\in \omega$ and 0 for $x\notin \omega$. We study the following problem in the infinitely long cylinder $\Omega$ with a concentrated nonlinear source on ∂ω:

$\begin{array}{l}{u}_t-\Delta u=\alpha \frac{\partial {\chi }_{\omega }\left(x\right)}{\partial \upsilon }f\left(u\right)\text{in}\Omega \times \left(0,T\right],\\ u\left(x,0\right)=0\text{on}\bar{\Omega },u\left(x,t\right)=0\text{on}\partial \Omega \times \left(0,T\right],\end{array}\}$ (1.1)

where α and T are positive real numbers, $\bar{\Omega }$ is the closure of $\Omega$, f is a given function such that ${\lim }_{u\to c^{-}}f\left(u\right)=\infty$ for some positive constant c, and f(u) and its derivatives $f^{\prime }\left(u\right)$ and $f^{″}\left(u\right)$ are positive for $0\le u<c$. The problems with a concentrated source on the surface of a ball in ${ℝ}^N$ have been studied by Chan and Tragoonsirisak ( [4] [5] [6] ).

A solution u of (1.1) is said to quench in a finite time if there exists a number $t_q\in \left(0,\infty \right)$ such that

$\text{sup}\left\{u\left(x,t\right):x\in \bar{\Omega }\right\}\to c^{-}\text{as}t\to t_q.$

For convenience, let $x=\left(x_1,x_2\right)$ be a point in the two-dimensional Euclidean space ${ℝ}^2$. Due to the symmetry, the three-dimensional problem (1.1) is equivalent to the following two-dimensional problem:

$\begin{array}{l}{u}_t-\Delta u=\alpha \frac{\partial {\chi }_B\left(x\right)}{\partial \nu }f\left(u\right)\text{in}D\times \left(0,T\right],\\ u\left(x,0\right)=0\text{on}\bar{D},u\left(x,t\right)=0\text{on}\partial D\times \left(0,T\right],\end{array}\}$ (1.2)

where ν(x) denote the unit outward normal at $x\in \partial B$, and ${\chi }_B\left(x\right)$ denote the function which is 1 for $x\in B$ and 0 for $x\notin B$. For ease of reference, since D is bounded, let us state the results by Chan [3] in the following theorem.

Theorem 1.1. There exists some $t_q$ such that for $0\le t<t_q$, the integral equation has a unique continuous nonnegative solution u. Furthermore, u is a nondecreasing function of t. If $t_q$ is finite, then at $t_q$, u quenches everywhere on ∂B only.

Note that D and B are both the balls centered at the origin. By radial symmetry, the problem (1.2) can be written in the polar form:

$\begin{array}{l}{u}_t-u_{rr}-\frac{1}{r}{u}_r=\alpha \delta \left(r-b\right)f\left(u\right)\text{in}\left(0,R\right)\times \left(0,T\right],\\ u\left(x,0\right)=0\text{on}\left[0,R\right],u_r\left(0,t\right)=u\left(R,t\right)=0\text{on}\left(0,T\right],\end{array}\}$ (1.3)

where $r=\left|x\right|$, and $\delta \left(r-b\right)$ is the Dirac delta function. Clearly, every solution u(r) of (1.3) is a radially symmetric solution of (1.2).

Green’s function corresponding to the problem (1.3) is given by

$g\left(r,t;\xi ,\tau \right)=\frac{2}{R^2}\underset{n=1}{\overset{\infty }{{\displaystyle \sum }}}\left\{\frac{\xi }{{\left[J_1\left(x_n\right)\right]}^2}{J}_0\left(\frac{x_n\xi }{R}\right)J_0\left(\frac{x_{n}r}{R}\right)\exp \left[-{\left(\frac{x_n}{R}\right)}^2\left(t-\tau \right)\right]\right\}$ (1.4)

where J₀ and J₁ are the Bessel functions of the first kind of order 0 and 1 respectively, and x_n is the n^th root of the Bessel function J₀(x). The integral equation corresponding to the problem (1.3) is given by

$u\left(r,t\right)=\alpha {\displaystyle {\int }_0^{t}g\left(r,t;b,\tau \right)f\left(u\left(b,\tau \right)\right)\text{d}\tau }.$ (1.5)

A solution u of (1.5) is said to quench in a finite time if there exists a number $t_q\in \left(0,\infty \right)$ such that

$\text{sup}\left\{u\left(r,t\right):r\in \left[0,R\right]\right\}\to c^{-}\text{as}t\to t_q.$

We note from Theorem 1.1 that $u\left(r,t\right)$ attains its maximum at $r=b$. If t_q is finite, then at t_q, u quenches only at $r=b$.

In Section 2, we show that there exists a unique positive number ${\alpha }^{*}$ such that u exists globally for $\alpha \le {\alpha }^{*}$ and quenches in a finite time for $\alpha >{\alpha }^{*}$. We also derive a formula for computing ${\alpha }^{*}$. In Section 3, we study the effects of b and R on quenching.

2. The Critical Value α^*

In this section, we study the effect of α on quenching. We modify the techniques used in proving Lemma 1 of Chan and Wong [7] for a singular parabolic problem to establish the following lemma.

Lemma 2.1. ${\lim }_{t\to \infty }{\displaystyle {\int }_0^{t}g\left(b,t;b,\tau \right)\text{d}\tau }$ is bounded.

Proof. The Green function from (1.4) can be written as

$g\left(b,t;b,\tau \right)=\frac{2}{R^2}\underset{n=1}{\overset{\infty }{{\displaystyle \sum }}}\left\{\frac{b}{{\left[J_1\left(x_n\right)\right]}^2}{\left[J_0\left(\frac{x_{n}b}{R}\right)\right]}^2\exp \left[-{\left(\frac{x_n}{R}\right)}^2\left(t-\tau \right)\right]\right\}.$ (2.1)

Since each term under the summation is positive and R is positive, $g\left(b,t;b,\tau \right)$ is also positive. Next, we will prove that the Green’s function (2.1) is bounded.

By using the asymptotic formula of $J_{\left(N-2\right)/2}\left(z\right)$ (cf. Zwillinger ( [8] , p. 562)),

$J_{\frac{N-2}{2}}\left(z\right)={\left(\frac{2}{\text{π}z}\right)}^{1/2}\left[\text{cos}\left(z-\frac{\text{π}}{2}\left(\frac{N-2}{2}\right)-\frac{\text{π}}{4}\right)+O\left(z^{-1}\right)\right]$ (2.2)

for large positive value z. Since $\left|\cos z\right|\le 1$ and $z^{-1}\to 0$ as $z\to \infty$, there exists a positive constant k₁ and z₀ such that for $z>z_0$,

$\left|z^{1/2}{J}_{\frac{N-2}{2}}\left(z\right)\right|\le k_1.$ (2.3)

Since $z^{1/2}{J}_{\left(N-2\right)/2}\left(z\right)$ is continuous on $\left[0,z_0\right]$, it follows from (2.3) that for $z\ge 0$, there exists a positive constant k₂ such that

$\left|J_{\frac{N-2}{2}}\left(z\right)\right|\le \frac{k_2}{z^{1/2}}.$

Let $N=2$ and $z=x_{n}b/R$. We have

$\left|J_0\left(\frac{x_{n}b}{R}\right)\right|\le \frac{k_2{R}^{1/2}}{{\left(x_{n}b\right)}^{1/2}}=\frac{k_2{R}^{1/2}}{{\left(x_n\right)}^{1/2}{b}^{1/2}}.$ (2.4)

For large n, it follows from (2.2) that

$J_{\frac{N-2}{2}}\left(x_n\right)={\left(\frac{2}{\text{π}{x}_n}\right)}^{1/2}\left[\text{cos}\left(x_n-\frac{\text{π}}{2}\left(\frac{N-2}{2}\right)-\frac{\text{π}}{4}\right)+O\left({\left(x_n\right)}^{-1}\right)\right],$

$J_{\frac{N}{2}}\left(x_n\right)={\left(\frac{2}{\text{π}{x}_n}\right)}^{1/2}\left[\text{sin}\left(x_n-\frac{\text{π}}{2}\left(\frac{N-2}{2}\right)-\frac{\text{π}}{4}\right)+O\left({\left(x_n\right)}^{-1}\right)\right].$ (2.5)

Since $J_{\left(N-2\right)/2}\left(x_n\right)=0$,

$\text{cos}\left(x_n-\frac{\text{π}}{2}\left(\frac{N-2}{2}\right)-\frac{\text{π}}{4}\right)+O\left({\left(x_n\right)}^{-1}\right)=0$

or

$\text{cos}\left(x_n-\frac{\text{π}}{2}\left(\frac{N-2}{2}\right)-\frac{\text{π}}{4}\right)\to 0\text{as}n\to \infty .$

Therefore,

$\sin \left(x_n-\frac{\text{π}}{2}\left(\frac{N-2}{2}\right)-\frac{\text{π}}{4}\right)\to 1\text{as}n\to \infty .$

Hence, there exists an integer N such that for $n>N$,

$\left|\sin \left(x_n-\frac{\text{π}}{2}\left(\frac{N-2}{2}\right)-\frac{\text{π}}{4}\right)\right|\ge \frac{1}{2}.$ (2.6)

From (2.5) and (2.6), we have

$\left|J_{\frac{N}{2}}\left(x_n\right)\right|\ge {\left(\frac{2}{\text{π}{x}_n}\right)}^{1/2}\cdot \frac{1}{2}={\left(\frac{1}{2\text{π}{x}_n}\right)}^{1/2}.$

By letting $N=2$, we have

${\left|J_1\left(x_n\right)\right|}^{-1}\le {\left(2\text{π}{x}_n\right)}^{1/2}.$ (2.7)

It follows from (2.1), (2.4) and (2.7) that

$\begin{array}{c}g\left(b,t;b,\tau \right)\le \frac{2}{R^2}\underset{n=1}{\overset{\infty }{{\displaystyle \sum }}}\left\{b{\left[{\left(2\text{π}{x}_n\right)}^{1/2}\right]}^2{\left[\frac{k_2{R}^{1/2}}{{\left(x_n\right)}^{1/2}{b}^{1/2}}\right]}^2\text{exp}\left[-{\left(\frac{x_n}{R}\right)}^2\left(t-\tau \right)\right]\right\}\\ \le \frac{4\text{π}{\left(k_2\right)}^2}{R}\underset{n=1}{\overset{\infty }{{\displaystyle \sum }}}\text{exp}\left[-{\left(\frac{x_n}{R}\right)}^2\left(t-\tau \right)\right]\end{array}$

which converges uniformly for t in any compact subset of $\left(\tau ,T\right]$.

Then, there exists a constant k₃ such that

$\begin{array}{c}{\displaystyle {\int }_0^{t}g\left(b,t;b,\tau \right)\text{d}\tau }\le \frac{k_3}{R}{\displaystyle {\int }_0^t\underset{n=1}{\overset{\infty }{{\displaystyle \sum }}}\text{exp}\left[-{\left(\frac{x_n}{R}\right)}^2\left(t-\tau \right)\right]\text{d}\tau }\\ =\frac{k_3}{R}\underset{n=1}{\overset{\infty }{{\displaystyle \sum }}}{\displaystyle {\int }_0^t\text{exp}\left[-{\left(\frac{x_n}{R}\right)}^2\left(t-\tau \right)\right]\text{d}\tau }\\ =\frac{k_3}{R}\underset{n=1}{\overset{\infty }{{\displaystyle \sum }}}\left\{\frac{R^2}{{\left(x_n\right)}^2}\cdot \left(1-\text{exp}\left[-\frac{{\left(x_n\right)}^{2}t}{R^2}\right]\right)\right\}\end{array}$

and

$\underset{t\to \infty }{\lim }{\displaystyle {\int }_0^{t}g\left(b,t;b,\tau \right)\text{d}\tau }\le k_{3}R\underset{n=1}{\overset{\infty }{{\displaystyle \sum }}}\frac{1}{{\left(x_n\right)}^2}.$

For large n, since $O\left({\left(x_n\right)}^2\right)=O\left(n^2\right)$ (cf. Watson ( [9] , p. 506)), ${\displaystyle {\sum }_{n=1}^{\infty }1/{\left(x_n\right)}^2}$ converges and bounded. Therefore, there exists a constant k₄ such that

$\underset{t\to \infty }{\lim }{\displaystyle {\int }_0^{t}g\left(b,t;b,\tau \right)\text{d}\tau }\le k_{4}R.$ (2.8)

Thus, the lemma is proved. +

Theorem 2.2. The solution u of (1.3) exists globally for α sufficiently small.

Proof. For any $t\in \left(0,t_q\right)$, it follows from Theorem 1.1 that u attains its absolute maximum at $r=b$. For $u\left(r,t\right)\le c/2$, since $f^{\prime }\left(u\right)>0$, we have $f\left(u\right)\le f\left(c/2\right)$. It follows from (1.5) and (2.8) that

$\begin{array}{c}u\left(b,t\right)\le \alpha f\left(\frac{c}{2}\right){\displaystyle {\int }_0^{t}g\left(b,t;b,\tau \right)\text{d}\tau }\\ \le \alpha f\left(\frac{c}{2}\right)\underset{t\to \infty }{\lim }{\displaystyle {\int }_0^{t}g\left(b,t;b,\tau \right)\text{d}\tau }\\ \le \alpha f\left(\frac{c}{2}\right)k_{4}R\end{array}$

for some constant k₄. By choosing α sufficiently small, namely,

$\alpha \le \frac{c}{2f\left(c/2\right)k_{4}R},$

we have $u\left(r,t\right)\le u\left(b,t\right)\le c/2$ for $t\in \left(0,\infty \right)$. Thus, the Theorem is proved. +

Theorem 2.3. The solution u of (1.3) quenches in a finite time for α sufficiently large.

Proof. From (1.4) and (1.5), we have

$u\left(r,t\right)=\frac{2\alpha b}{R^2}{\displaystyle {\int }_0^t\underset{n=1}{\overset{\infty }{{\displaystyle \sum }}}}\left\{\frac{J_0\left(\frac{x_{n}b}{R}\right)J_0\left(\frac{x_{n}r}{R}\right)}{{\left[J_1\left(x_n\right)\right]}^2}{\text{e}}^{-{\left(x_n/R\right)}^2\left(t-\tau \right)}\right\}f\left(u\left(b,\tau \right)\right)\text{d}\tau .$

At the maximum value $r=b$, since $f^{\prime }\left(u\right)>0$, we have

$\begin{array}{c}u\left(b,t\right)\ge \frac{f\left(0\right)2\alpha b}{R^2}{\displaystyle {\int }_0^t\underset{n=1}{\overset{\infty }{{\displaystyle \sum }}}}\left\{\frac{{\left[J_0\left(\frac{x_{n}b}{R}\right)\right]}^2}{{\left[J_1\left(x_n\right)\right]}^2}{\text{e}}^{-{\left(x_n/R\right)}^2\left(t-\tau \right)}\right\}\text{d}\tau \\ =\frac{f\left(0\right)2\alpha b}{R^2}\underset{n=1}{\overset{\infty }{{\displaystyle \sum }}}\left\{\frac{{\left[J_0\left(\frac{x_{n}b}{R}\right)\right]}^2}{{\left[J_1\left(x_n\right)\right]}^2}{\displaystyle {\int }_0^t{\text{e}}^{-{\left(x_n/R\right)}^2\left(t-\tau \right)}\text{d}\tau }\right\}\\ =f\left(0\right)2\alpha b\underset{n=1}{\overset{\infty }{{\displaystyle \sum }}}\left\{\frac{{\left[J_0\left(\frac{x_{n}b}{R}\right)\right]}^2}{{\left[J_1\left(x_n\right)\right]}^2{\left(x_n\right)}^2}\left(1-{\text{e}}^{-{\left(x_n/R\right)}^{2}t}\right)\right\}.\end{array}$

Since each term of the series is positive, we have

$u\left(b,t\right)\ge f\left(0\right)2\alpha b\cdot \frac{{\left[J_0\left(x_{1}b/R\right)\right]}^2}{{\left[J_1\left(x_1\right)\right]}^2{\left(x_1\right)}^2}\left(1-{\text{e}}^{-{\left(x_1/R\right)}^{2}t}\right).$

As $t\to \infty$,

$\left(1-{\text{e}}^{-{\left(x_1/R\right)}^{2}t}\right)\to 1.$

Thus, there exists some $\tilde{t}\in \left(0,\infty \right)$ such that for $t\ge \tilde{t}$,

$1-{\text{e}}^{-{\left(x_1/R\right)}^{2}t}\ge \frac{1}{2}.$

Then, for $t\ge \tilde{t}$,

$u\left(b,t\right)\ge \frac{f\left(0\right){\left[J_0\left(x_{1}b/R\right)\right]}^2\alpha b}{{\left[J_1\left(x_1\right)\right]}^2{\left(x_1\right)}^2}.$

By choosing α sufficiently large, say

$\alpha \ge \frac{{\left[J_1\left(x_1\right)\right]}^2{\left(x_1\right)}^{2}c}{f\left(0\right){\left[J_0\left(x_{1}b/R\right)\right]}^{2}b},$

we have $u\left(b,t\right)\ge c$ which implies that u quenches in a finite time. This proves the theorem. +

We state without proof of the following result since its proof is similar to that of Theorem 2.4 of Chan and Tragoonsirisak [10] for a quenching problem in an infinite strip.

Theorem 2.4. If $u\left(r,t\right)\le C$ for some constant $C\in \left(0,c\right)$, then $u\left(r,t\right)$ converges from below to a solution $U\left(r\right)={\lim }_{t\to \infty }u\left(r,t\right)$ of the nonlinear two-point boundary value problem:

$\begin{array}{l}-U_{rr}-\frac{1}{r}{U}_r=\alpha \delta \left(r-b\right)f\left(U\right)\text{in}\left(0,R\right),\\ U_r\left(0\right)=U\left(R\right)=0.\end{array}\}$ (2.9)

Moreover,

$U\left(r\right)=\alpha G\left(r;b\right)f\left(U\left(b\right)\right),$ (2.10)

where

$G\left(r;\xi \right)=\{\begin{array}{l}\xi \ln \left(R/\xi \right),0\le r\le \xi ,\\ \xi \ln \left(R/r\right),\xi <r\le R\end{array}$ (2.11)

is Green’s function corresponding to problem (2.9).

The next result shows that there exists a critical value ${\alpha }^{*}$ for $\alpha$. The proof of the following theorem is similar to that for Theorem 2.5 of Chan and Tragoonsirisak [10].

Theorem 2.5. There exists a unique ${\alpha }^{*}$,

${\alpha }^{*}=\frac{1}{b\ln \left(R/b\right)}\cdot \underset{0<U\left(b\right)<c}{\sup }\left(\frac{U\left(b\right)}{f\left(U\left(b\right)\right)}\right),$ (2.12)

such that u exists globally for $\alpha \le {\alpha }^{*}$, and u quenches in a finite time for $\alpha >{\alpha }^{*}$.

Proof. Let us construct a sequence $\left\{u_n\right\}$ in $\left(0,R\right)\times \left(0,T\right]$ by $u_0\left(r,t\right)=0$, and for $n=0,1,2,$...,

$\begin{array}{l}H{u}_{n+1}=\alpha \delta \left(r-b\right)f\left(u_n\right)\text{in}\left(0,R\right)\times \left(0,T\right],\\ u_{n+1}\left(r,0\right)=0\text{for}r\in \left[0,R\right],\\ \frac{\partial }{\partial r}{u}_{n+1}\left(0,t\right)=u_{n+1}\left(R,t\right)=0\text{for}t\in \left(0,T\right],\end{array}$

where $H=\partial /\partial t-{\partial }^2/\partial r^2-\left(1/r\right)\partial /\partial r$. From (1.5),

$u_{n+1}\left(r,t\right)=\alpha {\displaystyle {\int }_0^{t}g\left(r,t;b,\tau \right)f\left(u_n\left(b,\tau \right)\right)\text{d}\tau }.$ (2.13)

Since $f\left(0\right)>0$, and $g\left(r,t;b,\tau \right)>0$, it follows from (2.13) that $u_1\left(r,t\right)>u_0\left(r,t\right)$ in $\left(0,R\right)\times \left(0,T\right]$. Using the principle of mathematical induction, we have $0<u_1<u_2<\cdots <u_{n-1}<u_n$ in $\left(0,R\right)\times \left(0,T\right]$ for any positive integer n. Since $u_n$ is an increasing sequence as n increases, it follows from the Monotone Convergence Theorem (cf. Stromberg ( [11] , pp. 266-268)) that

$u\left(r,t\right)=\alpha {\displaystyle {\int }_0^{t}g\left(r,t;b,\tau \right)f\left(u\left(b,\tau \right)\right)\text{d}\tau },$

where ${\lim }_{n\to \infty }{u}_n\left(r,t\right)=u\left(r,t\right)$. To show that the larger the α, the larger the solution, let β be a positive number such that $\beta <\alpha$. We construct the sequence $\left\{v_n\right\}$ by $v_0\left(r,t\right)=0$, and for $n=0,1,2,$...,

$v_{n+1}\left(r,t\right)=\beta {\displaystyle {\int }_0^{t}g\left(r,t;b,\tau \right)f\left(v_n\left(b,\tau \right)\right)\text{d}\tau }.$

Similarly, we have $0<v_1<v_2<\cdots <v_{n-1}<v_n$ in $\left(0,R\right)\times \left(0,T\right]$, and

$v\left(r,t\right)=\underset{n\to \infty }{\lim }{v}_n\left(r,t\right)=\beta {\displaystyle {\int }_0^{t}g\left(r,t;b,\tau \right)f\left(v\left(b,\tau \right)\right)\text{d}\tau }.$

Because $u_n>v_n$ for any positive integer n, we have $u\ge v$. Hence, the solution u is a nondecreasing function of α. Since the solution u of the problem is unique, it follows from Theorems 2.2 and 2.3 that there exists a unique ${\alpha }^{*}$ such that u exists globally for $\alpha <{\alpha }^{*}$ and quenches in a finite time for $\alpha >{\alpha }^{*}$.

The critical value ${\alpha }^{*}$ is determined as the supremum of all positive values α for which a solution U of (2.9) exists. Since U(r) attains its maximum at $r=b$, it follows from (2.10) and (2.11) that

$U\left(b\right)=\alpha b\ln \left(\frac{R}{b}\right)f\left(U\left(b\right)\right).$

Hence, we have (2.12).

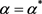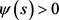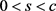To show that u exists globally when, we consider the function. Since for, and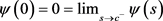, a direct computation shows that 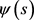attains its maximum when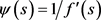, where 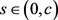by the Rolle Theorem. Thus, 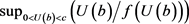occurs with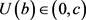. This implies that when, 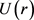exists and is bounded away from c. Therefore, u exists globally when. +

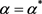For illustration, let. By a direct computation, attains its supremum at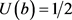. Hence, for given R and b, we have

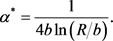
3. Critical Location of the Source b^* and Radius R^*

In this section, we fix α, and study the effect of the location of the source b and the effect of the radius R on quenching.

Lemma 3.1.

1) If

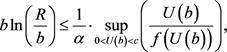(3.1)

then u exists globally.

2) If

(3.2)

then u quenches in a finite time.

Proof. 1) (3.1) is equivalent to. By Theorem 2.5, u exists globally.

2) Since (3.2) is equivalent to, it follows from Theorem 2.5 that u quenches in a finite time. +

Let ϕ be a function given by.

Lemma 3.2. ϕ(b) attains its maximum at. Note that.

Proof. We have

which is equal to 0 when. Since

by the second derivative test, ϕ(b) attains its maximum at. +

Theorem 3.3. For given α and R,

1) if

then u exists globally for any b.

2) if

there exist and such that u exists globally for or, and quenches in a finite time for.

Proof. 1) Using Lemmas 3.1 and 3.2, the theorem can be proved.

2) We have

(3.3)

We note from the assumption that

To solve

(3.4)

for b, since the constant on the right-hand side is smaller than the maximum of the function on the left-hand side, it follows from (3.3) that (3.4) have two solutions. Let us denote the solution less than R/e by, and the one larger than R/e by. From Lemmas 3.1 and 3.2, we have proved the theorem. +

We note from Theorem 3.3 (1) that when R is sufficiently small, u exists globally for any location of the source b.

Corollary 3.4. For given α, there exists a unique

such that u exists globally for. For, the solution may or may not quench (depending on the location of the source b).

For illustration, let, and. A direct computation gives. From Corollary 3.4,

If R is smaller than or equal to e/4, then u exists globally (for any location of the source b). If R is larger than e/4, then the quenching may occur (depend on the location of the source b). Let. By using a graphing calculator to solve (3.4), namely,

it follows from Theorem 3.3 (2) that we have and (round to four decimal places).

4. Conclusions

Our analysis of the nonlinear parabolic problem (1.1) shows that the strength of the source, the size of the domain and the location of the concentrated source inside the domain have impacts on the occurrence of quenching. When the strength of the source and the size of the domain are large enough, it was found that the quenching can be prevented by locating the concentrated source sufficiently close to the boundary of the cylinder.

The fractional diffusion problem with a concentrated source in one-dimensional domain was recently studied ( [12] [13] ). Many problems in the real world involve more than one dimension. Based on the current study here, the fractional diffusion problem with a concentrated source in multi-dimensional domain would be the future work.

Acknowledgements

The author thanks the referees for their suggestions.

Conflicts of Interest

The author declares no conflicts of interest regarding the publication of this paper.

References

[1]	Kawarada, H. (1975) On Solutions of Initial-Boundary Value Problem for ut=uxx+1/(1-u). Publications of the Research Institute for Mathematical Sciences, 10, 729-736. https://doi.org/10.2977/prims/1195191889
[2]	Chadam, J.M. and Yin, H.M. (1993) A Diffusion Equation with Localized Chemical Reactions. Proceedings of the Edinburgh Mathematical Society, 37, 101-118. https://doi.org/10.1017/S0013091500018721
[3]	Chan, C.Y. (2006) Multi-Dimensional Quenching Due to a Concentrated Nonlinear Source. Differential Equations and Dynamical Systems (DCDIS Proceedings), Vol. 2, 273-278.
[4]	Chan, C.Y. and Tragoonsirisak, P. (2008) A Multi-Dimensional Quenching Problem Due to a Concentrated Nonlinear Source in RN. Nonlinear Analysis, 69, 1494-1514. https://doi.org/10.1016/j.na.2007.07.001
[5]	Chan, C.Y. and Tragoonsirisak, P. (2009) Effects of a Concentrated Nonlinear Source on Quenching in RN. Dynamic Systems and Applications, 18, 47-54.
[6]	Chan, C.Y. and Tragoonsirisak, P. (2011) A Multi-Dimensional Blow-Up Problem Due to a Concentrated Nonlinear Source in RN. Quarterly of Applied Mathematics, 69, 317-330. https://doi.org/10.1090/S0033-569X-2011-01219-3
[7]	Chan, C.Y. and Wong, B.M. (1989) Periodic Solutions of Singular Linear and Semilinear Parabolic Problems. Quarterly of Applied Mathematics, 47, 405-428. https://doi.org/10.1090/qam/1012266
[8]	Zwillinger, D. (2003) CRC Standard Mathematical Tables and Formulae. 31st Edition, Chapman and Hall/CRC, New York, 562. https://doi.org/10.1201/9781420035346
[9]	Watson, G.N. (1944) A Treatise on the Theory of Bessel Functions. 2nd Edition, Macmillan, New York, 506.
[10]	Chan, C.Y. and Tragoonsirisak, P. (2013) Quenching Criteria for a Parabolic Problem Due to a Concentrated Nonlinear Source in an Infinite Strip. Quarterly of Applied Mathematics, 71, 541-548. https://doi.org/10.1090/S0033-569X-2013-01315-3
[11]	Stromberg, K.R. (1981) An Introduction to Classical Real Analysis. Wadsworth, Belmont, 266-268.
[12]	Sawangtong, W. and Sawangtong, P. (2017) A Single Quenching Point for a Fractional Heat Equation Based on the Riemann-Liouville Fractional Derivative with a Nonlinear Concentrate Source. Boundary Value Problems, 1, 97. https://doi.org/10.1186/s13661-017-0830-9
[13]	Chan, C.Y. and Liu, H.T. (2018) Existence of a Solution for the Problem with a Concentrated Source in a Subdiffusive Medium. Journal of Integral Equations and Applications, 30, 41-65. https://doi.org/10.1216/JIE-2018-30-1-41