Stochastic Dynamics of Cholera Epidemic Model: Formulation, Analysis and Numerical Simulation ()
1. Introduction
It is well known that diseases have impacts on people’s health. Therefore, it is necessary to study the mechanism by which the disease spread, conditions for the disease to have minor or major outbreak and get the knowledge on how to control the diseases such as cholera, Ebola, etc. In this study we are mainly concern with cholera epidemic. Cholera is an infectious disease that causes severe watery diarrhea, which leads to dehydration and even death if untreated. According to WHO report [1] , about 1.4 to 4.3 million cases of cholera are reported each year worldwide and more than 140,000 deaths per year are reported due to cholera. As a result of this, several mathematical models have been developed to model cholera epidemics, through these models one can predict the behaviour of the disease and control the particular epidemic. Any epidemic of an infectious disease can be modelled by using either deterministic or stochastic models. The deterministic models are formulated as a system of ordinary different equations and are preferred by many researchers since its analysis is simple compared to stochastic models. However, the shortcomings of deterministic models are: they give less information, rely on the law of large numbers, difficulty to do estimation, when the population is very small it becomes difficult to do analysis and also, experimentally the measured trajectories do not behave as predicted due to some random effects that disturb the system [2] .
Due to these limitations of ordinary differential equations in modelling infectious diseases, stochastic modelling of infectious diseases in both heterogeneous and homogeneous population emerged as an alternative to deterministic model and alleviated some of the problems of deterministic models in modelling epidemic diseases. In reality many phenomena in nature are usually affected by stochastic noise and the ordinary differential Equation (ODEs) models ignore the stochastic effects [2] . The stochasticity can be added to the ODEs by including the random terms or elements by parametric perturbation technique. This technique introduces other parameters to the model known as noise intensities.
Many of the models that have been employed in water-borne settings have been deterministic, thus ignoring the possible effects of randomness; see, e.g. [3] [4] [5] [6] [7] . These models incorporate an environmental pathogen component that is the concentration of the vibrios into a SIR (susceptible-infected-recovered) and SIsIaR (susceptible-symptomatic infected-asymptomatic infected-recovered) epidemic framework. Some of these models only considered compartment I as a single compartment (individuals with severe symptoms only) (e.g. [3] [4] [5] [6] ) instead of splitting it into two heterogeneous groups that are symptomatic and asymptomatic infected individuals to study the transmission dynamics of cholera epidemic. Also, some of these models considered only direct transmission of disease i.e., human to human and other models ignored the feedback loop from infected individuals to the environment reservoir. However, in their studies no stochastic models considered, so as to keep track where the disease is at continuous time and not only at discrete time as shown in their studies.
In [7] they developed deterministic model by extending the work by [6] . The work in [6] considered infected individuals (I) as a homogeneous group that is people with severe symptoms like vomiting and diarrhoea. Therefore, [7] divided infected individuals (I) into symptomatic infected (Is) and asymptomatic infected (Ia), in order to observe the contribution of concentration of Vibrio cholerae in the environment through excretion from each compartment and hence how it leads to the transmission dynamics of cholera epidemic.
In the stochastic modeling of cholera epidemic few papers emphasized on cholera stochastic models. [8] developed a deterministic model and further, extended it stochastic differential equations, the limitations to their paper are: no numerical analysis considered in their paper and compartment I is considered as single compartment, it could be better to split it into two groups, individuals with severe symptoms (symptomatic infected individuals) and those with mild symptoms (asymptomatic infected individuals) so as to observe the contribution of these two groups to the concentration of Vibrio cholerae through excretion.
[9] [10] developed a simple deterministic and stochastic model to discuss the spread of cholera. In their paper, they described the spread of cholera by modeling the bacteria population in contaminated water and human interaction with the bacteria in the water supply. The limitation to their paper is the absence of enough theoretical and numerical analysis. In [11] proposed a deterministic model that described the interaction among the two types of vibrios and viruses. The deterministic model proposed was further extended to include the random effects and from the stochastic model formulated it indicated that there is always a positive probability of disease extinction within the human host.
In this paper, we extend the deterministic model developed in [7] by formulating an equivalent stochastic differential Equation (SDEs). The formulated stochastic differential Equation (SDEs) models will be analyzed theoretically using suitable Lyapunov functions, Itô formula and some stochastic techniques. Numerical simulation will be carried using Euler-Maruyama scheme and extended Kalman filter. Also, maximum likelihood estimation method will be used to estimate the model parameters.
In the next section, we present a deterministic cholera epidemic model with water treatment, which is a model formulated by [7] . In Section 3, the corresponding two different stochastic models are formulated using parametric perturbation technique and transition probabilities approach. In Section 4, the formulated stochastic differential equations are analyzed by proving the existence and positivity of solutions, stochastic boundedness, global stability in probability, moment exponential stability, and almost sure convergence. In Section 5, the numerical results from the deterministic and stochastic simulations are presented, discussed and compared. In Section 6, we provide a brief discussion to support our findings. Ultimately, the last section concludes our paper.
2. Cholera Deterministic Model
From the description of the dynamics of cholera as shown in Figure 1, we the following set of ordinary differential equation system as in [7] .
(1)
with suitable initial conditions. The total human population is given by
.
From the model:
,
,
,
and
refer to susceptible individuals, symptomatic infected individuals, asymptomatic infected individuals, recovered individuals and the pathogen concentration in the contaminated environment respectively. The model parameters are described as follows.
b is the birth rate or recruitment rate,
is rate of exposure to contaminated water,
is the concentration of Vibrio cholerae in water,
is the contribution
![]()
Figure 1. The interaction of cholera epidemic transmission dynamics between compartments is shown.
of
to the population of Vibrio cholerae through excretion,
is the contribution of
to the population of Vibrio cholerae through excretion, d death rate due to cholera,
death rate of Vibrio cholerae due to water treatment,
is the mortality rate for bacteria including phage degradation,
is the recovery rate of symptomatic infected individuals,
is the recovery rate of asymptomatic infected individuals, p is the prob. of new infected from
to be symptomatic, q is the prob. of new infected
to be asymptomatic ,
is the natural death rate.
The key parameter in epidemiology is the basic reproduction number, which is defined as the average number of secondary infectious cases transmitted by a single primary infectious cases introduced into a whole susceptible population [12] . This parameter is useful because it helps determine whether an infectious disease will spread within the population or not. To compute
, the next generation matrix approach is used as in [13] . It is obtained by taking the largest (dominant) eigenvalue value (spectral radius) of
where
is the rate of appearance of new infection in compartment i,
is the net transition between compartments,
is the disease free equilibrium and
stand for the terms in which the infection is in progression i.e.,
,
and
in the model (1). Hence, the basic reproduction number obtained in [7] was as follows:
(2)
where
From Equation (2), when
, the highly infectious vibrios will not grow within human host and the environmental vibrios ingested into human body will not cause cholera infection. But when
the human vibrios will grow and persist, and hence leads to human cholera.
3. Stochastic Differential Equations
In this section we provide two approaches of formulating stochastic differential equations from the deterministic model (1). These approaches are parametric perturbation Itô SDEs and Itô SDEs from the transition probabilities.
3.1. Parametric Perturbation Itô SDEs
The idea of parametric perturbation is to choose a parameter of interest from the deterministic model and change it to random variable [14] [15] . In this study we introduce the randomness into the model by replacing parameters
and d by
and
, where
and
are two independent standard Brownian motions with the following properties:
1)
a.s,
2) For all times
, the increment
is normally distributed with zero mean and variance
; i.e.,
,
3) For all times
, the increments
of the process are independent random variables,
4) All samples paths
, are continuous
a.s.
Similarly,
and
are real constants, known as the intensities of the stochastic environment.
From the deterministic model (1) we get the following system of stochastic differential equations:
(3)
with suitable initial conditions. The technique of parameter perturbation introduces another parameters
and
in a model.
3.2. Itô SDEs with Transition Probabilities
This method was proposed by [16] [17] , the stochastic differential equations follow from the diffusion process. The nature of stochastic differential equation to be formulated is in this form:
(4)
where
is a matrix satisfying
[16] [17] ,
is the co-variance to order
,
is the approximate covariance matrix,
is the vector of independent Wiener process,
is a vector of parameters and
is the drift part or deterministic part.
From Equation (1) we formulate an equivalent SDEs as
(5)
where
and
. Clearly,
is an Itô process,
such that
. Then,
, corresponds to the number of individuals
respectively and
the Vibrio cholerae concentration in the environment. However,
is not a compartment occupancy as the other one are so its transition is not considered in the formulation of transitions.
In order to find the expectation
and covariance matrix
, we need to consider the transition probabilities as stated in Table 1. The transition probabilities are formulated from Equation (1). From Table 1, the expectation and variance co-variance matrix are computed as follows:
(6)
On substituting the values of
,
and
to Equation (6), we get
and the co-variance matrix is given by
![]()
Table 1. Possible changes in the process for the
model.
(7)
Also, by substituting the values of
,
and
to Equation (7), we get
where
The Itô stochastic differential equation, where global Lipschitz conditions are satisfied to ensure the existence and uniqueness of strong solution, can be written as in Equation (4) as found in [14] . Hence by Equation (5), the Itô stochastic differential equations become:
(8)
Note that if
and
, then cholera epidemic stops.
4. Analysis of Parametric Perturbation Itô Stochastic Differential Equation Model
In this paper, unless otherwise stated, we let
be a complete filtered probability space, with
satisfying the usual conditions (i.e., increasing and right continuous also
contains all
-null sets). Let
where
4.1. Global Existence and Uniqueness of Positive Solutions
Before proving the existence and uniqueness of positive solutions, let us state the conditions that guarantee the existence and uniqueness of solution of Equation (4).
Lemma 1. Assume that there exist two positive constants
and K such that
1) (Lipschitz condition) for all
and
2) (Linear growth condition) for all
Theorem 1. For any initial value
, there is a unique solution
to system (3) for all
, and the solution will remain in
with the probability 1, namely
, for all
almost surely.
Proof. Since the coefficients of system (3) satisfy the local Lipschitz condition, then for initial values
, there is unique local solution
on
, where
is the first hitting time or explosion time. In order to prove that the solution is global and positive, we need to show that
a.s. Let
be sufficiently large so
that
remain within the interval
. For
integer
. Let
be any random variable (taking eventually infinite value) on a filtered probability space
. We say that
is a stopping time for filtration
if at each (deterministic) time
, the event
is known in
. In this study we define
Let
be empty set then the
. By definition
increases as
. Let
, then
a.s. We need to show that
a.s. Then
and
. If this statement is false we say that, there exist
and a constant
, such that
. As a consequence to this, there exist an integer
such that
(9)
For
and at each k,
(10)
where
. Then
(11)
where
and
Define now
the Lyapunov function
by
(12)
and
. Then
is an Itô stochastic process with the SDEs given by
(13)
which becomes
(14)
where
Hence
(15)
From
, it follows that
(16)
where
is a positive constant independent of variables
and time t. Then we obtain
(17)
let
. Introduce integral to Equation (17)
(18)
Introducing the expectation to Equation (18) and by the Gronwall inequality, leads to
(19)
where
. Since the mean of stochastic integral equals zero [18] . Then let
from inequality (9), we have
. Then for all
, there must exist at least one of
which can take either
or k. Hence we have
(20)
again define the indicator function on
denoted by
be defined for all
by
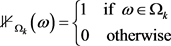
From Equation (19) and by Bienayme Chebyshev inequality we have
 (21)
(21)
when
, this leads to contradiction as
Therefore, we conclude that for the solution
of cholera model not to explode at finite time with probability 1, we need to have
a.s. This completes the proof. □
Theorem 1 shows that the solution of model (3) will remain in
. Next, we give the definition of stochastic ultimate boundedness [19] , which is very important in population dynamics.
Definition 1. The solution
of model (3) are said to be stochastically ultimately bounded, if for any
, there is a positive constant
, such that for any initial value
, the solution
to Equation (3) has a property that
Theorem 2. The solutions of system (3) are stochastically ultimately bounded for any initial value
.
Proof. From Theorem 1, we showed that
remain in
, for all
almost surely.
Let
,
and
be lyapunov functions stated as
(22)
Taking their derivatives with respect to
we get
(23)
Using Itô formula we get
(24)
but
(25)
where
(26)
(27)
Therefore
(28)
There exists positive constants
,
and
such that
(29)
It follows that
(30)
Then
(31)
For
and consider the case of
. Then from the holders inequality we have
(32)
consequently we have
(33)
where
is a suitable constant.
There exists a positive constants
such that
Given
and let
, then by Bienayme Chebyshev inequality
(34)
Hence
This completes the proof as required. □
4.2. Moment Exponential Stability
The moment exponential stability of the equilibrium solutions of stochastic differential Equation (3) are established from the idea of Lyapunov function [20] .
Lemma 2. Consider a function
satisfying these inequalities:
and
,
where
and p are positive constants. Then the equilibrium solution of Equation (3) is pth moment exponentially stable. When
, it is usually said to be exponentially stable in mean square and the DFE is globally asymptotically stable.
Lemma 3. When
and
. Then
Theorem 3. If
and
, the disease free equilibrium of the model system (3) is pth moment exponentially stable in
.
Proof. Given that
, as from Theorem 1 the solution of the system remains in
. Set
, then consider Lyapunov
function
, we have
(35)
In
, we have
, such that
, then from the fact that
, as
, there exists
such that
, Then LV becomes
(36)
Applying the idea of Lemma 3, we can formulate some of the inequalities as follows
(37)
On substituting these inequalities in Equation (19), we get
(38)
Hence
(39)
where
and
. If we choose
sufficiently very small, then we can choose
positive such that the coefficients
become negative.
Hence, according to Lemma 2 the proof is complete. □
4.3. Almost Sure Convergence
Theorem 4 If
, then
converge almost surely exponentially to (0, 0, 0).
Proof. Let
. As
, define the lyapunov function as
, such that
. Using Itô formula we get
(40)
But
, also by dropping some of the negative terms in Equation (40) we obtain
(41)
(42)
When
, then disease die out and hence
. Therefore
(43)
Let
. It follows that
(44)
Introducing integral both sides from 0 to t to Equation (44) we get
(45)
Then from the strong law of large number for local martingale we have
(46)
Hence, from Equation (45) and Equation (46) we have that
This completes the proof. □
Theorem 5. If
, then the disease free equilibrium
is almost surely stable in
.
Proof. Define a Lyapunov function as follows
Applying the Itô formula to function V above we get
(47)
From Equation (47) let
and
, then
(48)
(49)
let
Then,
becomes
(50)
Then,
deduce to
(51)
since
we have
(52)
Applying integration from 0 to t both sides to Equation (52), we get
(53)
Then, for all time
, the quadratic variation of the Itô integral process
is deterministic integral over
of
i.e.,
(54)
where C is a constant. Then by strong law of large number for local martingales, we have
(55)
From Equation (54) and (55), we conclude that
This completes the proof 5. □
Theorem 6. If
, then
converge almost surely to
Proof. We are required to show that
Consider the first equation of model system (3), let
. Using Itô formula we have
(56)
Applying integration both sides from 0 to t to Equation (56), we get
From the fact that
and from Theorem 4, we have in
that
(57)
Hence
(58)
Also
(59)
Combining Equation (57) and (59), we get
(60)
If
does not converge almost surely to
, there is
such that the
, then for all
, it follows that
Then, there exists,
such that
We have
(61)
Then, as
, where
It implies that
. But from Equation (57), we see that
. This leads to contradiction.
Hence,
This completes the proof of Theorem 6. □
5. Numerical Results
In this section, we numerically solve the ordinary differential Equation (ODEs) model (1) and stochastic differential Equation (SDEs) model (3) and (8) by fourth order Runge-Kutta and Euler-Maruyama scheme respectively. The behaviour of individuals sample path of the stochastic differential equation models are compared to the deterministic solution. Initially, one infective is introduced into a population. The time step is
and the time axis is the number of time steps, e.g., Time = 100 means 100 time steps and thus, an actual total time of
. The Euler-Maruyama scheme is one of the numerical methods for computing the sample paths of SDEs (3) and (8) [21] . This method is a finite difference approximation
(62)
From Equation (62), the vector
is j independent standard normal random numbers
. Also,
, and
is chosen sufficiently very small to ensure good convergence. The sample path of the
stochastic differential equations is shown in Figure 6. It is observed that the sample path is continuous but not differentiable (a Wiener process property).
Maximum likelihood estimation method is used to estimate the unknown parameters
of a SDE (8) by maximizing the likelihood [16] .
Let
be the transition probability density of
given vector
. Suppose that the density of the initial state is
, in maximum likelihood estimation of
[16] , the joint density
(63)
is maximized over
. The value of
that maximizes
will be denoted by
. For simplicity, it is more convenient to minimize the function
(64)
where,
is computed recursively by extended Kalman filter and its approximation is
(65)
where
(66)
is the Jacobian matrix of
,
,
is the measurement at time
,
is the state at time
,
is the vector of parameter to estimated,
is the covariance matrix of the measurement error at
. However, at
the state is assumed to have the prior distribution. For more details on EKF (see [22] ).
The estimated parameters by MLE are shown in Table 2. It is observed that the estimates are close to the true parameter values. Figures 2-5 show the extended Kalman filter estimates together with the true solution from ODE, measurements and states. Here black line, blue line and green line represents ODE solution, measurements and states realizations respectively. It is observed that the extended Kalman filter fits the states, which means states
can easily be estimated. The stochastic model (3) can be re-written in the following discretization equations:
(67)
![]()
Figure 2. The sample path of
for SDE (8) and deterministic solution for
graphed with extended Kalman filter estimates.
![]()
Figure 3. The sample path of
for SDE (8) and deterministic solution for
graphed with extended Kalman filter estimates.
![]()
Figure 4. The sample path of
for SDE (8) and deterministic solution for
graphed with extended Kalman filter estimates.
![]()
Figure 5. The sample path of
for SDE (8) and deterministic solution for
graphed with extended Kalman filter estimates.
where
is the Gaussian random variables
. The Euler-Maruyama scheme is used to simulate the sample paths of stochastic differential Equation (3) and the result is graphed in Figure 6. From Figure 6, we observe that the susceptible proportion eventually converges to zero; the entire population becomes infected, and later they recover from the disease. Also, the sample path of
stochastic differential equations is continuous but not differentiable (a property of Wiener process).
The sample path of
stochastic differential equations model together with the solutions of ordinary differential equations is graphed in Figure 7. From Figure 7, we find that the sample path of
stochastic differential equations model fluctuates within the solution of the
ordinary differential equation model.
6. Discussion
We have proposed a new modeling framework for the dynamics of cholera using both deterministic and stochastic models. Our focus is on the interaction of environmental vibrios to human (which causes the transformation from the environmental vibrios to human) and the infected individuals shedding bacteria into the environment. For deterministic model, we derived the basic reproduction number
. The basic reproduction number is a critical parameter for disease dynamics. In the deterministic model, the value of the basic reproduction number
determines the persistence or extinction of the disease. If
, the disease is eliminated, whereas if
, the disease persists in the population. From the deterministic model we have formulated two stochastic differential equations using parametric perturbation and transition probabilities methods.
![]()
Figure 6. The sample path of
for SDE model (3) when
,
and
.
![]()
Figure 7. The sample path of
for SDE model (3) are graphed with the deterministic solutions (dashed curve) when
,
and
.
We have proved the existence and uniqueness of positive solution, we showed that the solution of stochastic model are stochastically ultimately bounded, we derived that when
, then the infected compartments and bacteria goes to extinction. We carried out numerical simulation using Euler-Maruyama scheme to simulate the sample paths of stochastic differential Equation (3). Our results show that, the sample paths are continuous but not differentiable (a property of Wiener process) Also, we carefully compared the numerical simulation results for deterministic and stochastic models. We find that, the sample path of
stochastic differential equations model fluctuates within the solution of the
ordinary differential equation model as seen in Figure 7. However, the model parameters of SDEs are estimated by maximum likelihood estimation method. It is shown that the estimates are close to the true parameter values as seen in Table 2. Also, we used extended Kalman filter to estimate the states (compartments) of stochastic model (8) by recursively computing the transition probability density. It is observed that the state estimates fit the measurements as seen in Figures 2-5. Hence, we find that both models that are deterministic and stochastic models are very useful in understanding the dynamics of cholera epidemic. Nevertheless, Stochastic differential equation models are more important than deterministic models since they incorporate random effects such as environmental stochasticity and this enables us to model different quantities such as probability of extinction, probability of distributions and variances which cannot be captured in deterministic models.
7. Conclusions
In this paper, two stochastic differential equations models are formulated from the deterministic model using two different approaches: parametric perturbation and Transition probabilities. For deterministic model, the basic reproduction number
determines whether the disease is eliminated or persists in the given population.
For stochastic model, the perturbed stochastic differential equation is first analyzed by proving the existence and positivity of the solutions. Secondly, we looked at the stability aspect of the model; we proved that the number of symptomatic infected, asymptomatic infected and bacteria tends to asymptotically to zero exponentially almost surely. Also, we showed that the equilibrium solution of the SDEs is pth moment exponentially stable and it is usually said to be exponentially stable in mean square. Numerical simulations are carried to simulate the sample paths of stochastic models by Euler-Maruyama scheme and the
![]()
Table 2. Estimated model parameters for cholera epidemic by MLE.
solutions of deterministic model by fourth order Runge-Kutta method. It is observed that the sample paths are continuous but not differentiable (a property of Wiener process) and the sample paths of stochastic differential equations models fluctuate within the solutions of deterministic model. However, the model parameters of SDEs are estimated by maximum likelihood estimation method. It is shown that the estimates are close to the true parameter values. Also, extended Kalman filter is used to estimate the states of stochastic model by recursively computing the transition probability density. It is observed that the state estimates fit the measurements. So, we can say that cholera transmission dynamics can be modeled using stochastic differential equations. It is clear that real world problems such as disease are not deterministic in nature so including random effects to the model gives us a more realistic way of modeling cholera epidemics and other epidemic diseases. For example, using stochastic differential equation model we managed to examine the limiting asymptotic distribution of the number of symptomatic infected, asymptomatic infected and bacteria.
Acknowledgements
The authors wish to thank Pan African University and Tanzania Public Service College for their financial support and reviewers for the insightful comments that made this manuscript better.