Regional Productivity, Job Turnover and Profitability under Hukou Allocation System ()
1. Introduction
Sources of productivity disparities across regions have been studied in recent years (Ciccone and Hall [1] ; Deng and Jefferson [2] ). Understanding mechanism that generates regional productivity differences is of primal interest to economists and policy makers, because regional development hinges crucially on productivity improvement. In this paper, we try to contribute to this line of research by investigating a source of productivity difference between the two largest cities in China, Beijing and Shanghai.
Figure 1 shows that GDP per worker of Beijing is consistently lower than that of Shanghai during the period of 1998 to 2009. Past studies have attributed this productivity difference to such factors as R & D investment and technological progress (Zhang et al. [3] ), density of economic activity (Rizov and Zhang [4] ; Cai, Wang and Du [5] ), and economic structures (Li and Haynes [6] ; Chan and Zhang [7] ). Although these factors
![]()
![]()
![]()
Figure 1. GDP per person employed, average wage and labor turnover in Shanghai and Beijing. Note: GDP per person employed was calculated by dividing the GDP by employment. The Job- Finding rate is the fraction of unemployed persons that flow out of unemployment, and Job-Se- paration is the fraction of workers who leave their jobs. Source: China Statistical Yearbook 1998- 2015, National Bureau of Statistics of China; China Labour Statistical Yearbook 1998-2015, Department of Population and Employment Statistics of National Bureau of Statistics of China and Ministry of Labour and Social Security of China.
certainly influence the productivity level, this paper offers an alternative mechanism that explains this observed productivity difference. More specifically, we argue that the productivity difference stems from two cities’ Hukou allocation system (China’s house- hold registration system). We view Hukou as work-related benefits and build a theoretical model, where Beijing firms are entitled to allocate Hukou to their employees and can utilize it as a device for economizing on labor costs. In contrast, these Hukou are allocated to workers directly from the city authorities in Shanghai. The key mechanism of the model is that some Beijing firms find it optimal to retain mismatched workers, because Beijing’s Hukou allocation policy allows them to set wages to a lower level and this advantage outweighs a loss in output due to lower productivity. Because of this firm’s optimal behavior, the GDP per worker, the turnover rate and the wage are lower in Beijing than in Shanghai. This prediction is consistent with the statistics on these variables reported in Figure 1.
The fundamental lesson from this study is that the level of regional productivity can be low due to inefficiency arising from the retention of mismatched workers when Hukou are allocated to workers through their employer rather than being allocated to them directly. This insight can be applied to a wide range of economic issues concerning work-related benefits. This is especially valuable for immigration policy, because a work permit in some countries can be regarded as a work-related benefit.
The paper is organized as follows. Section 2 describes the main features of the Hukou allocation system. Section 3 provides a simple model where a firm’s optimal behavior is derived. Section 4 discusses three main implications from the model. Section 5 presents the concluding argument.
2. Background
In China, the Hukou allocation policy has a significant impact on people’s standard of living because the quality of social services (e.g., education and medical services) that a person can potentially receive depends on where his or her Hukou is established, rather than where he or she lives. The details of the Hukou system have been extensively reviewed by many researches (e.g. Chan and Zhang [7] ), and a feature relevant to this paper is as follows: While the benefits attached to a Hukou are so attractive that workers may sacrifice a part of their compensation in order to acquire the Hukou, firms may use an assignment of Hukou strategically to attract and retain desirable workers. Thus, the Hukou allocation system likely affects regional economic activities.
The most notable difference in the Hukou allocation policy between Beijing and Shanghai is the process of allocating a new Hukou. The Shanghai city authorities allocate Hukou to part of workers directly after they become a permanent employee. On the other hand, a fixed amount of Hukou is first allocated to a firm in Beijing. After this, it is the firm that determines whether a worker establishes a Hukou in Beijing by providing this valuable Hukou to worker. This feature of the Beijing’s Hukou allocation policy allows Beijing firms to set lower wages in exchange for giving Hukou to their employees. Unlike other rewards, a firm cannot retract Hukou from its employees once they are already assigned to them, since the Hukou are their employees’ property, even after they quit the firm.
Hukou system is a powerful household registration institution that affects many fundamental aspects of life for hundreds of millions of Chinese as well as China’s economic development. Past studies have focused on examining its roles in obstructing migration (Goldstein and Goldstein [8] , Chan and Yang [9] ), industrialization and urbanization (Chan [10] ; Cheng and Selden [11] ), and inequity of social welfare (Liu [12] ; Afridi et al. [13] ). Recently, researchers have been increasingly aware of its broader ramification on Chinese society and regional economy. Yang, Xu, and Xiang (2003) [14] pointed out that the Hukou system slowed down economic growth in developed regions because it prevents lower cost labor force from moving to more developed regions from poorer areas. Ma (1999) [15] discussed that different regions have an uneven performance on economic development even though spatial patterns of interprovincial migration are very similar. Ma (1996) [16] showed that, compared with intra-provincial migration, inter-provincial migration is a more prominent factor of population redistribution and economic development at the national and regional levels, and suggested that Hukou system has a negative effect on regional development because it prevents interprovincial migration. However, most of the past studies on this topic maintain an assumption that the Hukou system is the same through all regions. In this paper, we relax this assumption and focus on the difference in Hukou allocation system between Beijing and Shanghai, and show that different Hukou allocation systems can change a path of economic development. This result is consistent with the finding from Ma (1999) [15] .
This paper is also related to research on the relationship between labor market institutions and firm productivity. Ishida (2005) [17] investigated how a unique management style of lifetime employment in Japanese labor market influences firm performances, and discussed that firms may not be better off under such lifetime employment. Besley and Ghatak (2008) [18] argued that firms can increase their output by using status rewards such as job title or a medal. Our paper is also related to a line of research on immigration policy for economic growth (Friedberg and Hunt, [19] ; Martin [20] ), since immigration permission in some country can be regarded as work-related benefit similar to Hukou.
We construct a theoretical model in which different Hukou allocation systems generate differences in productivity among regional economies. A key insight from this theoretical model is that a mismatch between firms and workers arising from a Hukou allocation system can be a source of regional productivity differences. Since the effects of Hukou system on regional economic growth have been usually examined from the viewpoint of rural-to-urban migration, our analysis shed a new light on this topic by offering an alternative explanation for regional productivity differences resulting from different Hukou systems.
3. Model
3.1. Environment
There are two cities, City B (Beijing) and City S (Shanghai), in the economy. While Hukou are allocated to workers directly from the city authorities in City S, these Hukou are allocated to workers through firms in City B and firms may use this advantage strategically to raise their profits. We consider a two-period model with a unit mass of risk-neutral firms and of risk-neutral workers in each city.
In both periods, each firm employs at most one worker to produce output. The amount of output the firm produces only depends on a matching quality between the firm and a worker. For simplicity, the matching quality is either a good matching (m = 1) or a poor matching (m = 0). The production function of firm i is given by
,
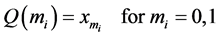where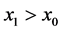 
is assumed.
Although the production function is identical across firms, they are heterogeneous with respect to the ability to draw a matching quality. Let q denote this ability and the variable q is assumed to be distributed uniformly over the unit interval between 0 and 1:
.
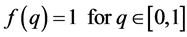A matching quality is determined randomly after hiring a worker. Specifically, firm i’s probability of drawing a given matching quality is given by
.
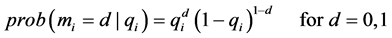The probability of drawing a good matching quality increases with firm’s ability q.
3.2. Employment Contract
In the first period, firms in both cities offer an employment contract that specifies wages for both periods. The contract offered by firm in City B also includes whether provide Hukou to the worker. The matching quality is unknown to both the firm and the worker at the beginning of the first period, but it is revealed completely at the end of the first period. At the beginning of the second period, the firm may dismiss its worker. To ease our explanation, we assume that renegotiation about the second period wage is never allowed after knowing the matching quality. We do not discount time.
3.2.1. Employment Contract in City S
In City S, a firm offers an employment contract so as to maximize its expected profit subject to a worker’s participation constraint. Formally, the firm’s maximization problem is
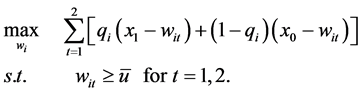
The optimal wage is simply given by
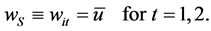
3.2.2. Employment Contract in City B
We assume that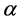 
fraction of the firms in City B obtain the right to entitle Hukou to their employee. For simplicity, Hukou are given to firms only in the first period. The wage setting is the same as the firms in City S, if a firm does not obtain this right. When a firm in City B obtains that right, its employment contract is determined by solving the following maximization problem:
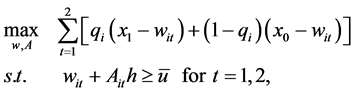
where A is a variable that equal to 1 if the Hukou is entitled and 0 otherwise, and h captures the level of benefit from obtaining a Hukou. Regardless of the firm’s decision on providing the Hukou to its worker, the optimal wage is set to
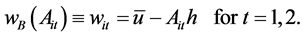
We turn to the decision on A. By setting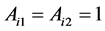
, the firm can save on the cost of both periods’ wages, if the firm decides to retain the worker in the second period. In addition, it can save on the cost of the first period’s wage, even when the firm dismisses the worker at the beginning of the second period. On the other hand, the firm is able to leave the entitlement of Hukou to the second period and set 
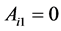and
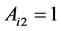, but this can only save the second period’s wage. Therefore, the firm’s profit is maximized when both 
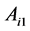and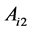 
are set to 1. By combining this result with the equation above, the optimal wage is given by
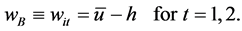
3.3. Decision on the Dismissal of a Worker
At the beginning of the second period, each firm knows the quality of match with the worker employed in the first period and makes a decision on whether to dismiss her. When the firm decides to retain the worker in the second period, she carries out the second period production. When the firm chooses to dismiss her, it hires a new worker who is drawn randomly from the pool of workers. Therefore, four possible firm behaviors in the second period: i) After knowing a good match between the firm and the worker, the firm retains the worker and receives output![]()
, ii) or it dismisses the worker and hires a new worker; iii) after knowing a poor match, the firm retains the worker and receives output![]()
, iv) or it dismisses the worker and hires a new worker.
3.3.1. Dismissal Decision in City S
To consider an optimal dismissal decision of a firm in City S, suppose that a good matching quality is realized in the first period. Taking the labor contract as given, the second period’s profit is ![]()
if the firm retains the well-matched worker, and the expected profit is ![]()
if it dismisses her and hires a new worker. Thus, the firm’s optimal decision in this case is to retain the well-matched worker, because ![]()
and![]()
. Next, consider the case where matching quality was poor in the first period. The second period profit is ![]()
when retaining the worker, and the expected profit is ![]()
when dismissing her. Hence, the firm in City S has no incentive to keep a poorly-matched worker.
Let Ds be a dummy variable that indicates 1 if a firm in City S dismisses its worker at the beginning of the second period and 0 otherwise. The firm’s optimal decision rule is simply expressed as
![]()
(1)
3.3.2. Dismissal Decision in City B
In this section, we consider an optimal dismissal decision by a firm in City B. First, consider the case where the firm does not have the right to entitle Hukou to its employee. This case is identical to firms in City S. The optimal decision for this type of firm (type NH) is given by
![]()
(2)
Next, consider the case where the firm has the right to entitle Hukou to its employee and uses it strategically to increase its profit. When a match is good, the profit in the second period is ![]()
if the firm retains the well-matched worker, and is ![]()
if dismisses the worker and hires a new worker. It is easy to see that the firm’s optimal decision in this case is to retain the worker.
When a poor matching quality is realized, the firm’s optimal decision is not straightforward and depends on the firm’s ability q. The second period profit is ![]()
if the firm retains the worker, and the expected profit is ![]()
if it dismisses her. Comparing these two profits yields
![]()
In other words, the firm dismisses its worker only when the matching quality is poor and the firm’s ability to draw a well-matched worker is sufficiently high. The optimal decision of such firms (type WH) can be expressed as
![]()
(3)
where ![]()
if ![]()
and ![]()
if![]()
.
4. Analysis
4.1. Job Turnover
We first compare the dismissal rate of the two cities. A dismissal rate is defined as the probability of dismissing workers at the beginning of the second period. As described in Equation (1), firms in City S dismiss all poorly-matched workers. The dismissal rate in City S is
![]()
(4)
Similarly, the dismissal rate of City B firms that do not possess the right to entitle Hukou is given by
![]()
.
The dismissal rate of City B firms that possess the right to entitle Hukou is
![]()
where![]()
. The dismissal rate in City B is now given by
![]()
(5)
Equations (4) and (5) imply that ![]()
because![]()
. Therefore, we have the following:
Proposition 1. The dismissal rate of City B is lower than that of City S.
The optimal behavior of firms in City S does not depend on the firm’s ability q, and they are able to dismiss a poorly-matched worker regardless of this ability. In contrast, the optimal behavior of City B firms depends on this ability. Those City B firms that use the Hukou strategically to lower wages do not dismiss a poorly-matched worker when their ability to draw a well-matched worker is low. Some inefficient matches between workers and firms are preserved under the allocation system where Hukou are given to firms directly.
4.2. Productivity
We assume that the population is the same in both cities, and then the total output measures their productivity. Since there is no difference in the first period total output between the two cities, we can only compare the second period total output.
In City S, for given q, the fraction q of firms drew a good match and produce ![]()
in the second period. The fraction ![]()
of firms hire a new worker in the second period and their expected output is![]()
. Therefore, the total expected output of City S in the second period is given by
![]()
(6)
Next, we consider the output level of City B. First, for firms that do not have the right to entitle Hukou to their employee, the case is identical to firms in City S, we have
![]()
We turn our attention to firms that have the right to entitle Hukou to their employee. For given q, the fraction q of firms drew a good match in the first period and produce ![]()
in the second period. On the other hand, the fraction ![]()
of firms drew a poor match in the first period. Those firms that satisfy ![]()
hire a new worker in the second period and their expected output is![]()
. Those firms that satisfy ![]()
continue to employ the poorly-matched worker and produce ![]()
in the second period. The total expected output is
![]()
Finally, the total expected output of City B is given by
![]()
(7)
Since![]()
, the third term in equation (7) is negative. We have the following implication:
Proposition 2. The total output of City B is smaller than that of City S.
Some firms in City B retain a worker even if a poor matching quality between the firm and worker is realized. This inefficient match lowers the aggregate productivity of City B, and the third term in equation (7) captures a loss of total output due to the Hukou allocation system. Note that the third term in equation (7) can be written as![]()
. Loss of total output increases with ![]()
and h. Since the main source of the distortion is the Hukou allocation system, the loss of total output increases when more firms can strategically use the advantage to construct their labor contract. A higher level of utility associated with Hukou allows more firms to retain a poorly-matched worker, which also results in a larger loss of total output. On the other hand, the loss of total output decreases with![]()
. Retaining a poorly-matched worker forgoes a possibility of hiring a well-matched worker and producing high output level![]()
, whereas its benefit comes from keeping a low wages. When a gap between ![]()
and ![]()
is large, the cost outweighs the benefit, and firms avoid retaining a poorly- matched worker.
4.3. Profit
This section compares firm profits of both cities. In doing so, we assume that the law of large numbers is satisfied. The total profit of firms in City S is
![]()
(8)
The total profit of firms in City B that do not possess the right is
![]()
and the total profit of firms that possess the right is
![]()
We thus have
![]()
(9)
Note that the forth term in equation (9) is positive because it can be written as ![]()
and we have ![]()
and![]()
. This generates the following implication:
Proposition 3. The total profit of City B is larger than that of City S.
While the first term in the square bracket of equation (9) reflects a productivity loss, its second term is a profit gain arising from wage saving. Proposition 3 says that this profit gain exceeds the productivity loss, and it confirms that a lower level of productivity is justified at the firm level by larger profits.
5. Conclusions
We provided an analysis that helps understand the effect of the Hukou allocation system on productivity, and offered an alternative explanation for an observed difference in firm productivity between Beijing and Shanghai. Our theoretical analysis indicated that the Beijing’s Hukou allocation system results in keeping an inefficient match between workers and firms, which, as argued before, is a source of lower productivity in Beijing. This paper demonstrates that the way of allocating Hukou affects not only worker’s welfare, but also regional development.
Note that for simplicity we assumed that all workers are identical and wage renegotiation is not allowed. In a more realistic model, however, workers would possess different level of ability and also have the right of wage renegotiation. This may affect some conclusions of this paper because firms and workers likely act so as to influence bargaining power and it may in turn change the nature of the mismatch problem we discussed above. Nonetheless, the model in this paper captures the fundamental relationship between Hukou allocation system and productivity, and provides meaningful implications for economic development policies.