Electrohydrodynamics Instability of Three Periodic Streaming Fluids through Porous Media

Sameh A. Alkharashi^1,2

¹Quesna Technical College, Tanta Technical Commercial Institute, Ministry of Higher Education, Egypt.
²Applied Sciences Department, College of Technological Studies, The Public Authority for Applied Education and Training (PAAET), Adiliya, Kuwait.

DOI: 10.4236/oalib.1101315                

Abstract

In this work, the effect of transverse horizontal electric field on the stability of three layers of immiscible liquids is illustrated. The fluids are subjected to a uniform horizontal electric field. Analytical and numerical simulations of this system of linear evolution equations are performed. The solutions of the linearized equations of motion and the boundary conditions lead to deriving two simultaneous Mathieu equations of damping terms having complex coefficients. The effects of the streaming velocity, the permeability of the porous medium, and the electrical properties of the flow on the instability are investigated. In the case of uniform velocity, it is found that electric field has a stabilizing influence on the stability criteria. When the periodicity of the velocity is considered, the method of multiple scales is applied to obtain stability solution for the considered system. It is found that the phenomenon of the dual role is found for increasing the permeability parameter. In addition it is found that the velocity of the middle layer has a destabilizing effect whereas the dielectric constant ratio has an opposite influence to the stability of the fluid layers.

Keywords

Stability Analysis, Fluid Layers, Horizontal Field, Porous Media, Mathieu Equations

Subject Areas: Fluid Mechanics

1. Introduction

The flow through porous media is of considerable interest for petroleum engineers and in geophysical fluid dynamicists. A series of studies for hydrodynamics stability have been initiated by many authors, for example, the unsteady electrohydrodynamic stability has been investigated in article [1] . The stability analysis is made of a basic flow of streaming fluids in the presence of an oblique periodic electric field. The authors in the paper [2] have discussed the instability of viscous potential flow in a horizontal rectangular channel. Bhatia [3] has stu- died the influence of viscosity on the stability of the plane interface separating two incompressible superposed fluids of uniform densities, when the whole system is immersed in a uniform horizontal magnetic field. He has developed the stability analysis for two fluids of equal kinematic viscosities and different uniform densities. Zakaria et al. [4] have investigated the instability properties of streaming superposed conducting fluids through porous media under the influence of uniform magnetic field, where the system is composed of a middle fluid sheet of finite thickness embedded between two semi-infinite fluids.

A good account of hydrodynamic stability problems has also been given in papers [5] - [9] . Li et al. [10] have examined the electrohydrodynamic stability of the interface between two superposed viscous fluids in a channel subjected to a normal electric field. The long wave linear stability analysis is performed within the generic OrrSommerfeld framework for both perfect and leaky dielectrics. The approach proposed in paper [11] is limited to study the gravity-driven flow of a liquid film below an inclined wall with periodic indentations in the presence of a normal electric field. Espn et al. [12] have analyzed the effect of viscoelasticity on the electrohydrodynamic instabilities in thin liquid films under the influence of AC and DC electric fields. It is found that the elasticity increases both the maximum growth rate and the corresponding wave number. In their study of AC electrohydrodynamic instabilities in thin liquid films, Roberts and Kumar [13] applied lubrication theory to examine the possibility of using AC electric fields to exert further control over the size and the shape of the pillars. They found that, for perfect dielectric films, linear stability analysis shows that the influence of an AC field can be understood by considering an effective DC field.

It is the purpose of our paper to develop a mathematical model for a steaming fluid sheet embedded between two bounded fluid layers in the presence of porous media. The fluids are subjected to a horizontal electric field. The present article is structured as follows. This section has presented the motivation for the investigation in addition to relevant background information. The next section lays down the exposition of the problem and a sketch of the system under consideration. Also in this section the equations of motion and boundary conditions are derived. The third section is prepared to linear perturbation and the line of solutions. In the fourth section, the Mathieu equations, for a periodic velocity, have been derived to control the surface wave propagation. Also, in this section, the perturbation scheme using the multiple scales analysis and the numerical estimation for stability configuration have been discussed. The results are discussed and some important conclusions are drawn in the final section of this paper.

2. The Basic Flow and exposition of the Problem

Consider parallel flow of three fluids in an infinite, fully saturated, uniform, homogeneous and isotropic porous media with constant permeability, where we assume a model of a liquid sheet sandwiched between two bounded fluid layers. The two interfaces between the fluids are assumed to be well defined and initially flat and forms the plane and the instantaneous perturbed interface height is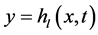, is along the y direction. The system is considered to be influenced by the gravity force in the negative y-direction as shown in Figure 1. The fluids are incompressible and have constant properties. There are two interfaces between the fluids are assumed to be well defined and initially flat and the two interfaces are parallel and the flow is each phase is every where parallel to each other. Assuming that the layers are moving with velocity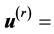

, where 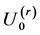and 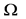are constants. The unit vectors 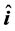and are in x- and y-directions.

The equations governing two-dimensional motion of an incompressible fluid through porous medium are given by the phenomenological Darcy equation, which comes from the combination of the momentum equation and Darcy’s law [11] - [14] :

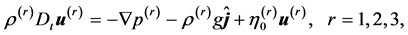(1)

associated with the continuity equation

(2)

In these equations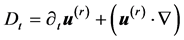, the partial derivatives of any function are denoted by the subscripts

Figure 1. Schematic of problem geometry.

t, x and y. The ratio represents to the resistance parameter, where the permeability 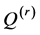describes

the ability of the fluid to flow through the porous medium and is the fluid viscosity measures the resis-

tance of fluid to shearing that is necessary for flow. The symbol is the horizontal gradient opera-

tor, the function refers to the fluid pressure and the parameter is the density of the fluids. Intro-

ducing the velocity potential of the perturbed motion such that the total fluid velocity is given by

(3)

and thus will satisfy Laplace equation

(4)

In a magneto-quasi-static system with negligible displacement current, Maxwell’s equations in the absence of free currents are

(5)

Here, is the electric field intensity vector, the notation × refers to the vector product of two vectors and refers to the dielectric constant. The construction of a potential function, can be representable as the gradient of the scalar potential such that

(6)

automatically satisfies zero curl for a constant permittivity and therefore the electrostatic potential satisfies the Laplace equation

(7)

The Maxwell stress tensor describes the stress field induced in the material due to electrostatic forces whose expression is

(8)

where, is the identity tensor. In the following, the boundary conditions are used to complete the solutions of the above system of the governing equations. These constraints are information about the solutions at the upper and lower boundaries and at the interfaces between the fluids [7] - [10] .

On the interface, it is natural to impose the kinematic boundary conditions, the kinematic condition expresses the fact that the interface always comprises the same fluid particles, and therefore the function whose graph defines the interface satisfies simultaneously

(9)

In addition kinematic relation follows from the assumption that the normal component of the velocity vector in each of the phases of the system is continuous at the dividing surface:

(10)

Here, is the exterior pointing normal unit vector to the interfaces which has the form

where is the surface geometry defined by. The

boundary conditions on the upper and lower plates, in which the plates are assumed to be rigid and kept constant, this implies that:

(11)

The continuity of the normal and the tangential components of the electric displacement at the interface obeyed Maxwell’s conditions, and thus we have

(12)

(13)

Furthermore the dynamical boundary condition, where the normal stresses are balanced by the amount of the surface tension is

(14)

where, it is assumed that the fluid interfaces have surface tension coefficient and is the

corresponding unit tangent at the interface.

3. Linear Perturbation and Solutions

In order to discuss the stabilization of the present problem, the interfaces between the fluids will be assumed to be perturbed about its equilibrium location and will cause a displacement of the material particles of the fluid system. The amplitude of waves formed on the fluid sheet is assumed to be small. For a small departure from the equilibrium state, every physical perturbed quantity may be expressed as functions of both the horizontal and vertical co-ordinates as well as time:

(15)

where k is the wave number, which is assymed to be real and positive, the symbol i denotes , the imaginary number, and c.c. represents complex conjugate of the preceding terms and S stands for and. These, expansions are introduced into the governing equations and the relevant boundary conditions. The linearized terms in these perturbed quantities are only maintained in view of the linear stability theory [15] [16] . To perform a linear stability analysis of the present problem, the interfaces between the three fluids will be assumed to be perturbed about their equilibrium locations to cause displacements of the material particles of the fluid system. Consider the effect of small wave disturbances to the interfaces, propagating in the positive x-direction. Assuming that the surface deflections are given by

(16)

where

(17)

and are arbitrary time-dependent functions which determine the behavior of the amplitude of the disturbances on the interfaces. Now by inserting Equation (3) into Equation (1), we obtain the pressure in terms of the velocity potential such that

(18)

Hence, from Equations (14) and (18), the balance at the dividing surfaces gives

(19)

In accordance with the interface deflection given by (17) and in view of a standard Fourier decomposition, we may similarly assume that the bulk solutions are of the form

(20)

(21)

As is customary in hydrodynamic stability analysis [15] , we determine the boundary-value problem cited above. It constitutes a homogeneous system of equations and boundary conditions for explaining the factors governing the surface wave’s propagation. In view of the above boundary conditions, the solution of Laplace's equation yields the distribution of the velocity potential and the magnetic potential in the three layers. Insert (20) into Laplace’s Equation (4); the resulting solutions in view of the above kinematic boundary conditions yield

(22)

(23)

(24)

Substituting (21) into Laplace’s Equation (7), the resulting solutions in view of the previous Maxwell’s conditions will give

(25)

(26)

(27)

where,

In the above solutions the stream velocity and the velocity potential function are made dimensionless using

and, while the applied normal field and the electric potential are made dimensionless by

and, respectively. In addition the viscosity, permeability of the

porous medium. And by using the symbols, the density

, , the Weber number,.

4. The Characteristic Equations

In this section our goal is to study effect of general surface deformations on the onset of a periodic velocity applied to the fluid sheet. Equations that determine the surface deflections are called the characteristic equations. Substituting Equations (22)-(24) and (25)-(27) into the normal stress tensor (19), to replace the dependence on the potential velocity, the electric stream function and the fluid pressure function by the dependence on the amplitude, finally after a straightforward calculations, one obtains the coupled equations

(28)

(29)

where the coefficients that appear in these equations are real and depend on the physical parameters of the problem. The mathematical formulas of these coefficients are lengthy and not included here. However, they are available upon request from the author. Equations (28) and (29) are two coupled Mathieu equations having damping terms and complex coefficients. By making use of these equations, the stability behavior of the fluid sheet is controlled. For a uniform stream, the periodicity of the stream will be absent. Therefore, wave propagation is excited by using the electro-capillarity technique. Hence, in the limiting case of tending to zero in the above system, the damped Mathieu equations then become a linear differential equations with constant coefficients. It can be satisfied by a growth rate solution, which may be written as

(30)

where is the constant of integration. Substituting this equation into the above system of Mathieu equations the dispersion equation of the perturbed motion is then

(31)

where the coefficients a’s are clear from the context. It should be noted that (31) represents a complex linear dispersion relation that is satisfied by values of and k. It is clear that the surface waves propagating along the interfaces separating between the inviscid fluids will only be stable if all the roots of (31) are real. Otherwise, there are at least two roots (complex conjugate) and thereby the interfacial inviscid waves are unstable. In Figure 2 our main goal is to examine the influence of the the applied electric field on the stability criteria of the system. However, the curves displayed in part (a) of Figure 2 clarify the four roots of the characteristic Equation (31) with the variation of the disturbance wave number k, corresponding to the case of the uniform stream, for a system having the parameters given in the caption of Figure 2. It is observed that all the roots of (31) are real and then admitting stable waves in the range satisfying the relation, while two of these roots are complex in the specific regions and. It is shown in part 2(b) with that the four roots of (31) are real in the region, whereas two of these roots are complex in the specific regions and. In part 2(c), where, we observe that the stable area is increased to become in the range, while the unstable range is decreased, in which we observe that one or two the roots of (31) have acquired real values. In comparison of the parts of Figure 2, we conclude that the electric field has a stabilizing influence on the movement of the waves where the increase of the values of the field has changed the unstable waves into stable waves. This case may be physically interpreted as suggesting that a part of the kinetic energy of the field has been absorbed from the waves. El-Sayed et al. [17] have obtained a similar conclusion in their studies of nonlinear electrohydrodynamic stability of two superposed Walters B’ viscoelastic fluids in relative motion through porous medium.

In the presence of the periodicity of the velocity, the stability picture has changed dramatically and hence we return to the general form of dispersion relations (28) and (29). The method of multiple time scales [18] has

Figure 2. The variation of the four roots of (31), corresponding to the the case of the uniform stream, with the disturbed wave number k, for a system having, , , , , , , , , , , , with, 0.6 and 1 of the partitions (a), (b) and (c), respectively.

been successfully used to treat similar these equations, since the solutions and the properties of Equations (28) and (29) are unknown. Applying the method of multiple scales, where the independent variable t can be extended to introduce alternative independent variables:, , where the parameter represents a small dimensionless parameter characterizing the steepness ratio of the wave. Thus, we define as the variables appropriate to fast variations and, as the slow variables. The differential operators can now be expressed as the derivative expansions:

(32)

where is the time of the lowest order. For the small dimensionless parameter, we can characterize the

amplitude of the periodic force which is defined as. The analysis then follows the usual perturba-

tion procedure and suppression of the secular terms except that is now more convenient to write the solution in a complex form.

Now, let the dependent variables be expanded in the form

(33)

Substituting (32) and (33) into (28) and (29) and equating coefficients of like powers of (because each of the are independent of) yields simpler inhomogeneous equations, which can be solved successively with knowledge of the solutions of the previous orders. Uniform solutions are required to eliminate the secular terms. This elimination produces the solvability conditions corresponding to the terms containing the factor, in which the solvability condition is divided into two cases. The first is valid in the non-resonant case in which the frequency is away from the frequency. Otherwise the resonance arises when the frequency approaches the frequency. Hence the solvability condition in the non-resonant case is

(34)

This condition show that the motion is stable if

(35)

In the resonance case when the frequency approaches the frequency, we introducing a detuning parameter defined by

(36)

and hence the solvability conditions are

(37)

where is the complex conjugate of. The solution of Equation (37) imposes a dispersion relation. This dispersion relation will be used to discuss the stability behavior in this resonant case. Let the solution of this equation has the form:

(38)

with real and. Substituting equation (38) into Equation (37) and separating the real and imaginary parts, if and are proportional to. Then the coefficients matrix must vanish for non-trivial solution. This yields the following dispersion relation:

(39)

where,. An important feature of the waves is that the growth or decay is according to the

sign of. In view of the Hurwitz criterion [18] , the stability of Equation (39) arises when

(40)

(41)

are satisfied. Condition (40) is the same as condition (35) which satisfies in the non-resonant case and the values of are the roots of the Equation (40), which are:

(42)

The curves and represent the transition curves in the plane that separate the stable

region from the unstable one. According to Fleque’s theory [18] of linear differential equations with periodic

coefficients, the region bounded by the two branches and is unstable, while the area outside them is

stable along which are periodic with a period of the other. It is clear that the two branches and

have common fixed points known as the resonant points. The emergence of these branches occurs as

tends to zero in Equation (36).

In graphing the stability picture, numerical computations are made for the resonant cases discussed above. The stability characteristics are governed by equations (42) which require the specification of the same parameters which we indicated in the case of the uniform stream. The resonant case of the frequency approaching the disturbance frequency is carried out. The numerical calculations for the transition and curves and in the resonant case of near are displayed in Figures 3-5.

Figure 3. The same system as that considered in Figure 2, but for, 2.5 and 3.5 of the partitions (a), (b) and (c), respectively.

Figure 4. The stability diagrams in the plane, according to Equations (42), at, 1.2 and 1.7 of the partitions (a), (b) and (c), respectively.

In Figure 3, is plotted against the wave number k. The graphs emphasize the impact of the variation of the above parameters. A numerical search was conducted to seek the regions of the stability and instability. The stable region involved in these graphs was decided by satisfying the inequalities (40) and (41), where S represents the stable region and U indicates the unstable case. The instability is due to the balance between the frequency and the disturbance frequency. The influence of the velocity is displayed in Figure 3, the stability diagrams that are shown in this graph represent two stable regions and other region that lies between the two transition curves and are unstable, which coincides with Floquet's theory. In Figure 3(a), we choose the velocity and select suitable values of the parameters which we indicated above. Inspection of the stability diagrams reveals that there is an unstable regions bounded by the transition curves and and other outside them which is stable. The increasing of velocity to the value under the same values of the other parameters is given in figure 3(b). The stability diagrams that are shown in these graphs illustrate that the unstable area increase, while the stable regions decrease. Thus, we conclude that the increase of the velocity has a destabilizing influence. In Figure 3(c), the stability diagrams that are shown in these graphs represent the same system as in the previous graphs while the velocity increases to the value, the unstable region increase and the stable regions decrease. It is apparent from the comparison between the graphs of Figures 3(a)-(c) that the variation of the velocity in middle layer plays a destabilizing role in the motion of the fluids.

In order to examine the influence the dielectric constant ratio the lower layer to the middle sheet on the

Figure 5. The graph is constructed for versus k, according to the transition curves given from condition (42), for the same system given in Figure 2, with, 3 and 5 of the partitions (a), (b) and (c), respectively.

stability criteria, numerical calculations are made in the parts of Figure 4 The graph shown in the plane are achieved for three values of the ratio, 1.2, and 1.7, corresponding to the partitions (a), (b) and (c) respectively, where the other quantities are held fixed. The inspection of the stability diagram of the parts of Figure 4 reveals that the increase of the dielectric constant ratio leads to increase in the width of the stability regions, while the unstable areas are decrease. The conclusion that may be drawn here is that the dielectric constant has a stabilizing influence on the stability behavior of the waves. In the parts (a), (b) and (c) of Figure 5, we repeat the same diagrams as illustrated in Figure 3, with a change in the value of the permeability of the porous media, while the other parameters are fixed. Applying the above stability constraints to separate the stable and the unstable regions, we notice that the the phenomenon of the dual role is found for increasing the value, which has two roles: one is a stabilizing influence at to and the other is a destabilizing influence when the permeability is increased from to 5.

5. Conclusion

In this paper, we introduce the stability of a fluid sheet of finite thickness embedded between two bounded layers of fluids through porous media. The system is under the influence of a horizontal electric field with a periodic stream. Through linear perturbation analysis in the general case where the surface deflections are assumed to be independent, the solution of the system in the use of normal stress condition leads to two simultaneous differential equations of Mathieu type with damping terms and having complex coefficients, which are used to control the stability of the fluid sheet motion. Consequently, a mathematical simplification is desired to relieve this complication for the Mathieu equation. Hence, the parametric instability arose in the standard way of the multiple scales method, which is used in order to derive stability criteria in the case of uniform streaming, and in resonant and non-resonant cases. The transition curves separating the stable region from unstable regions are identified. The analysis recovers the key numerical findings and provides qualitative understanding. Numerical calculation of the stability of the system is made where the physical parameters are put in the dimensionless form. The special case for the absence of periodicity of the velocity is discussed. They are found to be in exact agreement with the corresponding previous works in fluid mechanics and electro- hydrodynamics. Stability diagrams are plotted and discussed for different sets of physical parameters. Based on the numerical results, several conclusions can be drawn as follows: in the case of uniform velocity, it is found that electric field has a stabilizing influence on the stability criteria. When the periodicity of the velocity is considered, the method of multiple scales is applied to obtain stability solution for the considered system. It is found that the phenomenon of the dual role is found for increasing the permeability parameter. In addition it is found that the velocity of the middle layer has a destabilizing effect whereas the dielectric constant ratio has an opposite influence to the stability of the fluid layers.

Conflicts of Interest

The authors declare no conflicts of interest.

References

[1]	Elhefnawy, A.F. (1995) Intervals of an Unsteady Electrohydrodynamic Kelvin-Helmoltz Stability. Physica A, 214, 229-241. http://dx.doi.org/10.1016/0378-4371(94)00232-I
[2]	Funada, T. and Joseph, D.D. (2001) Viscous Potential Flow Analysis of Kelvin-Helmholtz Instability in a Channel. Journal of Fluid Mechanics, 445, 263-283. http://dx.doi.org/10.1017/S0022112001005572
[3]	Bhatia, P.K. (1974) Rayleigh-Taylor Instability of Two Viscous Superposed Conducting Fluids. Nuovo Cimento, 19B, 161-168.
[4]	Zakaria, K., Sirwah, M.A. and Alkharashi, S. (2009) Instability through Porous Media of Three Layers Superposed Conducting Fluids. European Journal of Mechanics-B/Fluids, 28, 259-270. http://dx.doi.org/10.1016/j.euromechflu.2008.08.002
[5]	Drazin, P.G. and Reid, W.H. (1981) Hydrodynamic Stability. Cambridge University Press, Cambridge.
[6]	Joseph, D.D. (1976) Stability of Fluid Motions II. Springer-Verlag, New York.
[7]	Sisoev, G.M., Matar, O.K., Sileri, D. and Lawrence, C.J. (2009) Wave Regimes in Two-Layer Microchannel Flow. Chemical Engineering Science, 64, 3094-3102. http://dx.doi.org/10.1016/j.ces.2009.03.044
[8]	Sadiq, I., Usha, R. and Joo, S.W. (2010) Instabilities in a Liquid Film Flow over an Inclined Heated Porous Substrate. Chemical Engineering Science, 65, 4443-4459. http://dx.doi.org/10.1016/j.ces.2010.04.005
[9]	Prieling, D. and Steiner, H. (2013) Analysis of the Wall Mass Transfer on Spinning Disks Using an Integral Boundary Layer Method. Chemical Engineering Science, 101, 109-119. http://dx.doi.org/10.1016/j.ces.2013.06.034
[10]	Li, F., Ozen, O. and Aubry, N. (2007) Linear Stability of a Two-Fluid Interface for Electrohydrodynamic Mixing in a Channel. Journal of Fluid Mechanics, 583, 347-377. http://dx.doi.org/10.1017/S0022112007006222
[11]	Tseluiko, D. and Blyth, M.G. (2008) Electrified Viscous Thin Film Flow over Topography. Journal of Fluid Mechanics, 597, 449-475. http://dx.doi.org/10.1017/S002211200700986X
[12]	Espn, L., Corbett, A. and Kumar, S. (2013) Electrohydrodynamic Instabilities in Thin Viscoelastic Films? AC and DC Fields. Journal of Non-Newtonian Fluid Mechanics, 196, 102-111. http://dx.doi.org/10.1016/j.jnnfm.2012.12.013
[13]	Roberts, S.A. and Kumar, S. (2009) AC Electrohydrodynamic Instabilities in Thin Liquid Films. Journal of Fluid Mechanics, 631, 255-279. http://dx.doi.org/10.1017/S0022112009006843
[14]	Dullien, F.L. (1992) Fluid Transport and Pore Structure. Academic, New York.
[15]	Chandrasekhar, S. (1961) Hydrodynamic and Hydromagnetic Stability. Oxford University Press, Oxford.
[16]	Moatimid, G.M. (2003) Stability Conditions of an Electrified Miscible Viscous Fluid Sheet. Journal of Colloid and Interface Science, 259, 186-199. http://dx.doi.org/10.1016/S0021-9797(02)00164-9
[17]	El-Sayed, M.F., Eldabe, N.T., Haroun, M.H. and Mostafa, D.M. (2013) Nonlinear Electrohydrodynamic Stability of Two Superposed Walters B’ Viscoelastic Fluids in Relative Motion through Porous Medium. Journal of Mechanics, 29, 569-582.
[18]	Nayfeh, A.H. (1979) Nonlinear Oscillations. Wiley, Hoboken.