An Empirical Investigation into the Effect of Enhancing Airline Capacity on Load Factor: A Case of Kenya’s Low-Cost Carriers ()
Received 18 May 2016; accepted 14 June 2016; published 17 June 2016

1. Introduction
Literatures on the low-cost carrier’s business model reveal that low-cost carrier phenomenon has proved to be a robust service concept from the financial and operational view point. However, studies have reported mixed results on the effect of enhanced low-cost carrier’s fleet capacity on load factor that varies from one region and/or country to the other. Attempts have attributed these variations and mixed results to the conceptualization and configuration of low-cost carrier business model which have led to the uneven spread of this model around the world due to differing catalytic factors such as regulatory framework, degree of entrepreneurship, density of population and relative wealth; travelling culture, airport availability, and adherence to internet facilities, and thus, a variation in the market development life cycle of low-cost carriers [1] - [3] . Whereas, fleet capacity has a significant impact on the number of equipment required [4] , the optimal number and size of equipment required depends on the: level of travel demand that the carrier will cover [5] - [7] , distance [8] , economies of scale in aircraft operation [9] [10] , airport characteristics such as runway, and whether hub-spoke or a point-to-point network [11] . Different studies [12] - [18] have investigated load factor variable differently. Reference [16] has employed descriptive statistics in analyzing the impact of fleet capacity on load factor. Both [15] and [17] have modeled load factor as a function of other independent variables. Reference [14] and [18] investigated it as an independent variable on the on-time performance while [12] and [13] investigated it as an explanatory variable on fare. As a result of the differing catalytic factors, empirical evidences have shown mixed results of the effect of enhancing airlines’ fleet capacity on load factor in different countries. It was for this reason that the purpose of this study was to ascertain the effect of the rising low-cost airlines capacity on load factor in the Kenyan airline market.
Section 2 briefly outlines the concept of low-cost carrier’s business model and the associated constructs, i.e. fleet capacity and load factor. In addition, previous studies are compared, contrasted, critiqued and the gap established. Section 3 outlines the methodology. Statistical tests for the assumptions of linear regressions, panel unit root tests, panel cointegration tests are performed in Section 3. Results and discussions are outlined in Section 4. Section 5 summarizes, concludes and provides recommendations.
2. Literature Review
This section reviews the concepts of low-cost carrier’s business model with an extension to specific constructs such as fleet capacity and load factor. Previous empirical studies are highlighted. Comparisons, contrasting, critiquing and acknowledgement of the gap from the reviewed literature is also established in this section.
2.1. Low-Cost Carrier Business Model
The chief difference between low-cost carriers and traditional airlines, or full service carriers (FSCs), fall into three groups: service savings, operational savings and overhead savings [19] . The low-cost model is characterized by specific product and operating features. Product features include: low, simple, and unrestricted fares; high frequencies; point-to-point flights; no interlining; ticketless travel utilizing travel agents and call centers; single-class, high density seating; no seat assignments; and no meals or free alcoholic drinks. Operating features include: single type aircraft with high utilization, secondary or uncongested airports served with short aircraft turns, short sector length, and competitive wages with profit sharing and high productivity [20] - [24] . However, [25] cited that there is no standard business model or definition for a low-cost carrier since the term itself incorporates a wide range of airlines with significant differences in the type of routes and the level of passenger service offered.
2.1.1. Fleet Capacity
The planning of demand-responsive transport services requires addressing two fleet-related decision problems: what types of equipment to use and how many to use [6] . Fleet size and mix (FSM) is of critical importance for a transport agency because it has an effect on both the costs of delivering the service (capital and operating costs) and the level of service (LOS) that can be provided to the clients in regard to comfort, convenience, and enjoyment [7] . Equipment capacity has a significant impact on the number of equipment required; the larger the equipment, the higher the average equipment productivity and the smaller the required number of fleet. Larger equipment should be used in high-demand cases [4] . The optimal number of equipment required depends on the level of travel demand that the carrier will cover [5] . The use of a mix of different fleet types, from small to medium and large that has more seats, have an advantage of the cost-effectiveness in dealing with variation in seating requirements as well as spatial and temporal clustering of requests. Larger fleet can accommodate, on a single trip, more passengers with different seating needs, which, in turn, can lead to higher productivity and fewer units required to deliver the service. The use of larger fleets however means higher capital and operating costs, higher emissions, and lower maneuverability. In situations of low demand, smaller fleets are often sufficient to handle the trips without any loss of efficiency. The use of a particular aircraft type on a route largely depends on the distance. As the distance between the two endpoints increases, longer-range (and thus larger) aircraft are needed. An airline may opt to use larger aircraft on a route due to economies of scale in aircraft operation [8] [10] [11] . With respect to airport characteristics, an increase in runway length results in higher frequency and larger plane sizes. Aircraft sizes are larger in a hub-spoke network than in a point-to-point network. Low cost carriers generally do not offer business class seating, which takes up a lot of valuable space, and instead offer a dense, single class seating configuration asother space consuming items, such as catering galleys and convection ovens, are eliminated.
2.1.2. Load Factor
Load factor is the percentage of seats filled with passengers or the ratio of unit costs to unit yields [9] [12] [21] [22] . A good load factor assures the necessary utilization and productivity of critical low cost carrier resources. Low load factors reflect delivery of larger-capacity equipment, while capacity reductions leads to significant increases in carriers’ load factor in the markets [26] . It indicates that an airplane is more efficiently utilized when the load factor is high, lowering the operating costs and, as a result, the airfares. A high load factor lowers cost per customer, but also lowers quality and demand [13] . The per passenger cost of a flight decreases as the load factor rises, which suggests that load factor has a negative coefficient on fare. Low cost carriers tend to have higher load factors than their competitors and thus, may result in prices falling on routes with a higher load factor [12] . High load factors are a major factor in low-cost carriers’ business model [27] who base the low-fare on the high occupancy rate of the aircraft (80% load factor) [28] . Low cost airlines’ load factors are usually higher than that of the traditional air transport companies, which means that each low cost company’s aircraft transport more passengers than network carriers [1] .
2.2. Empirical Studies
Studies by [12] - [18] had investigated load factor variable with respect to other aviation market parameters differently. Reference [12] treated it as an explanatory variable on fare and results show that the effect of load factor variable on pricing is negative and significant at the 1 percent level in the 80th percentile baseline equation; while for the median fare, it is negative and significant at the 2 percent level and is not significant for the lowest fares. On the other hand, [13] examined the impact of load factor on the mean fare paid among passenger-trips and his findings indicate that 10% decrease in average load factor would explain a price decline of about 15 percent. Reference [14] and [18] investigated load factor as an independent variable on the on-time performance while [13] investigated it as an independent variable on price. According to [14] ’s findings, results show that economic factors (seating capacity and load factor) and logistical factors (departure time and distance) have significant effects on flight delays. Reference [18] examined how load factor affects on-time performance. Their analyses show that the interaction of utilization and load factor is positive and significant for twelve out of thirteen carriers, meaning increasing load factor leads to greater delays when utilization is high, than when utilization is low. Reference [16] employed descriptive statistics in analyzing the impact of fleet capacity on load factor. Their report show mixed results on the impact of fleet capacity on load factor from one region, or continent to the other. For example, in the US, capacity grew at 1.9%, but load factor remained flat at 83.8 per cent. In China, capacity rose 12.2%, but load factor declined 0.6 percentage points to 80.3 per cent. In Japan, capacity expanded by 5.1% and load factor was little changed at 64.3 per cent. In Brazil, capacity reductions by airlines of 3.3% pushed load factor to 76.3 per cent. In India, capacity climbed 3.5% in 2013, and load factor was 74.6%, up 1.7 percentage points. In Russia, there was 9.1% rise in capacity and load factor remained at 74%. In Australia, capacity rose 3.8%, depressing load factor 1.0 percentage point to 76.5 per cent. While in Africa, there was capacity expansion of 5.2% and load factor rose 1.9 percentage points to 69%, the lowest among the regions. Both [15] and [17] modeled load factor as a function of other independent variables. Reference [15] ’s paper aimed at identifying serial and periodic autocorrelation on the load factors of the Europe-Mid East and Europe- Far East airline flights so as to develop a forecasting model of the load factors and their econometric estimation results also confirm that the load factors of the Europe-Mid East and Europe-Far East flights are both seasonal and differ between flights i.e. the load factor is still far from stable. Reference [17] results show that the number of seats is not significant in explaining the variation in load factors.
Due to variations in the market development life cycle of low-cost carriers from region and/or country to the other, empirical evidences have shown mixed results of the effect of enhancing airlines’ fleet capacity on load factor in different countries. It is for this reason that the purpose of this study was to ascertain the effect of the rising low-cost airlines capacity on load factor in the Kenyan airline market.
3. Research Methodology
This section addresses the research design, target population, type of data, statistical tests, and model specification.
3.1. Research Design, Target Population and Type of Data
The study adapted longitudinal design, which is a time series correlational research design that describes patterns of change and helps establish the direction and magnitude of causal relationships [29] - [31] . Their data from two low-cost carriers’ (Fly540, that formally operates as a low-cost carrier and Jetlink Aviation, which met the ICAO definition of a low-cost carrier in terms of operations but never used the term in marketing itself) over a period of 72 months for the year 2007 - 2012 were used in the analysis. Sources of data were airlines statistics as maintained by the Kenya Civil Aviation Authority (KCAA).
3.2. Statistical Tests
Testing the Assumptions of Linear Regression
Before linear regression models are used for purposes of inference or prediction, there are four principal assumptions which must be tested to justify its use. If any of these assumptions is violated, then the forecasts, confidence intervals, and scientific insights yielded by a regression model may be (at best) inefficient or (at worst) seriously biased or misleading [32] [33] . These assumptions are: (1) normality of the error distribution; (2) linearity and additivity of the relationship between dependent and independent variables; (3) statistical independence of the errors; (4) homoscedasticity (constant variance) of the errors.
1) Test for Normality of the error distribution
Violations of normality create problems for determining whether model coefficients are significantly different from zero and for calculating confidence intervals for forecasts. Since parameter estimation is based on the minimization of squared error, a few extreme observations can exert a disproportionate influence on parameter estimates [33] [34] . Calculation of confidence intervals and various significance tests for coefficients are all based on the assumptions of normally distributed errors [35] [36] . If the error distribution is significantly non-normal, confidence intervals may be too wide or too narrow. In this study, the researcher used Jarque-Bera statistical tests for normality. Jarque-Bera test statistic measures the difference of the skewness and kurtosis of the series with those from the normal distribution [37] ; the Jarque-Bera statistic should not be significant in cases of normal distribution. The statistic is computed as:
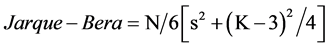 (1)
(1)
where S is the skewness, and K is the kurtosis.
Results in Table 1 show that FLTC series rejected the null hypothesis of normal distribution while LDFC series failed to reject the null hypothesis of normal distribution at the 5% significance level. However, real data, especially time series data, rarely has errors that are perfectly normally distributed, and it may not be possible to fit your data with a model whose errors do not violate the normality assumption at the 0.05 level of significance [33] [38] . The researcher then settled on the [32] ’s and [33] ’s conclusion that it is usually better to focus more on the violations of the other assumptions since normality is a very minor concern.
2) Tests for Linearity or Addivity
Violations of linearity or additivity are extremely serious. If one fits a linear model to data which are nonlinearly or non-additively related, your predictions are likely to be seriously in error. In order to test for linearity, the researcher adopted Ramsey RESET (Regression Specification Error Test) to detect any incorrect functional form as proposed by [39] . The RESET Stability tests statistics indicated no evidence of non-linearity as shown in Table 2.
Results in Table 2 show that the t-statistics strongly rejected any evidence of non-linearity.
![]()
Table 1. Results of normality test using Jarque-Bera.
![]()
Table 2. Ramsey RESET Linearity Test Results on the association between LDFC and FLTC.
3) Statistical independence of the errors
When data are ordered―for example, when sequential observations represent Monday, Tuesday, and Wed- nesday―then the neighboring error terms may turn out to be correlated. This phenomenon is called serial correlation [37] [38] . If left untreated, serial correlation can do two bad things: reported standard errors and t-statistics can be quite far off, and under certain circumstances, the estimated regression coefficients can be quite badly biased. While using the Durbin-Watson statistical test for serial correlation, under the null hypothesis (no serial correlation) the Durbin-Watson centers around 2.0 rather than 0. If the serial correlation coefficient is zero, the Durbin-Watson is about 2. As the serial correlation coefficient heads toward 1.0, the Durbin-Watson heads toward 0.
4) Homoscedasticity (constant variance) of the errors
OLS makes the assumption that the variance of the error term is constant (Homoscedasticity). If the error terms do not have constant variance, they are said to be heteroscedastic. Heteroscedasticity does not cause ordinary least squares coefficient estimates to be biased, although it can cause ordinary least squares estimates of the variance (and, thus, standard errors) of the coefficients to be biased, possibly above or below the true or population variance [40] [41] . Thus, regression analysis using heteroscedastic data will still provide an unbiased estimate for the relationship between the predictor variable and the outcome, but standard errors and therefore inferences obtained from data analysis are suspect. Biased standard errors lead to biased inference, so results of hypothesis tests are possibly wrong. If OLS is performed on a heteroscedastic data set, yielding biased standard error estimation, a researcher might fail to reject a null hypothesis at a given significance level, when that null hypothesis was actually uncharacteristic of the actual population (making a type II error).
Heterokedasticity, serial correlations and presence of outliers were never perceived by the researcher to be problems at all due to the fact that Fully Modified Ordinary Least Squares (FMOLS) had been adopted in the panel cointegrating equations as outlined by [42] - [45] . This method modifies least squares to account for serial correlation effects and for the endogeneity in the regressors that results from the existence of a cointegrating relationship, as well robustic in dealing with the outliers.
5) Panel Unit Root Tests
While dealing with panel data, which is usually time series in nature, researcher may have to find out if the data is stationary [46] . Stationarity of data is when the mean, variance and covariance are time invariant (they do not change over time). This was done by use of panel unit root tests; Yt is regressed on its lagged value Yt?1 and then checked if the estimated slope coefficient is statistically equal to 1. If not, then Yt is nonstationary. This then requires first differencing of Yt which is then regressed on Yt?1, if the slope coefficient is 0, then Yt is nonstationary, and if it negative, then Yt is stationary [41] [46] . Any series that is not stationary is said to be nonstationary.
PP Fisher Panel unit root testing was performed on the two variables. The results showed that LDFC was stationary at order 0, while the FLTC was stationary at order 1. The following 3 tables (Tables 3-5) show the results of the panel unit root analysis for the series:
The results in Table 3 failed to reject the null hypothesis of the presence of a unit root. Thus, it was necessary to difference the series.
![]()
Table 3. Panel Unit Root Test Results for the zero-order FLTC series.
![]()
Table 4. Panel Unit Root Test Results for the first-order FLTC series.
![]()
Table 5. Panel Unit Root Test Results for the zero-order LDFC series.
The results in Table 4 now shows that the first order FLTC series is now stationary given that the null hypothesis of the presence of a unit root is now rejected.
The results in Table 5 indicate that the null hypothesis of the presence of a unit root is rejected.
6) Panel Cointegration Tests
The finding that many macro time series may contain a unit root has spurred the development of the theory of non-stationary time series analysis [37] . Reference [47] pointed out that a linear combination of two or more non-stationary series may be stationary. If such a stationary linear combination exists, the non-stationary time series are said to be cointegrated. The stationary linear combination is interpreted as a long-run equilibrium relationship among the variables. Given that most of variables were not stationary at order zero, it was necessary to carry out cointegration tests before deploying the more favorable panel cointegrating regression due to its more accuracy in estimations. The panel cointegration tests were carried out by use of Pedroni Residual Cointegration Tests that evaluate the null hypothesis of no cointegration at the conventional size of p < 0.05against both the homogeneous and the heterogeneous alternatives. Table 6 shows that nine of the eleven statistics rejected the null hypothesis of no cointegration at the conventional size of 0.05.
![]()
Table 6. Panel Cointegration (Pedroni Residual) Test for the combined LDFC and FLTC series.
3.3. Correlational Analysis
Results in Table 7 indicate that fleet capacity has a significant positive correlation with load factor (r = 0.47, p-value = 0.000) respectively. This means that if fleet capacity increases, load factor will increase too.
3.4. Panel Regression Equation
By combining time series of cross-section observations, panel data give more informative, more variability, less collinearity among variables, more degrees of freedom and more efficiency [41] [47] . Panel data presents two big advantages over ordinary time series or cross section data. The not always obvious advantage is that in certain circumstances panel data allows you to control for un-observables that would otherwise mess up the regression estimation. A key assumption in most applications of least squares regression is that there aren’t any omitted variables which are correlated with the included explanatory variables (Omitted variables cause least squares estimates to be biased). Panel data allows for the use of fixed effects to make up for the omitted variable. Thus, to examine the influence of the fleet capacity on load factor, the following panel regression equations will be used:
To test if FLTC predicts LDFC →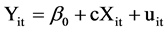 (2)
(2)
where:
𝔦 = 1, 2 and is the individual airline dimension (cross-section identifier);
t = time period (1 to 72);
C is the overall effect of the independent variable X on Y;
β0 is the intercept (cross-section fixed effects) for the equation;
u is the error terms(both person-specific and idiosyncratic) in the equation.
4. Results and Discussions
4.1. Descriptive Statistics
From Table 8, fleet capacity has a mean of 295.35 seats while the mean of load factor is 65.38%, this is consistent with the finding of [16] which reported a mean of 65.3% for African airlines during the year 2012 but far much lower than [3] ’s finding of 80% in Croatia. Median is the middle value (or average of the two middle values) of the series when the values are ordered from the smallest to the largest. The median of fleet capacity is 284 seats, while the median of load factor is 65 percent.
Std. Dev. (standard deviation) is a measure of dispersion or spread in the series. The standard deviation is given by:
 (3)
(3)
where N is the number of observations in the current sample and 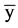 is the mean of the series. The standard
is the mean of the series. The standard
![]()
Table 7. Correlational analysis between fleet capacity and load factor.
![]()
Table 8. Summary of the descriptive statistics.
deviation of fleet capacity is 179.7 seats, and that of load factor is 9.01 percent. Skewness is a measure of asymmetry of the distribution of the series around its mean. Skewness is computed as:
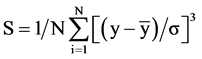 (4)
(4)
where σ is an estimator for the standard deviation that is based on the biased estimator, for the Variance (σ = s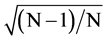 ). The skewness of a symmetric distribution, such as the normal distribution, is zero. Positive skewness means that the distribution has a long right tail and negative skewness implies that the distribution has a long left tail [35] [49] . Both fleet capacity and load factor are positively skewed as indicated by the values 0.16 and 0.11 respectively, this means that the mass of the distribution is concentrated on the right. Kurtosis measures the peakedness or flatness of the distribution of the series. Kurtosis is computed as:
). The skewness of a symmetric distribution, such as the normal distribution, is zero. Positive skewness means that the distribution has a long right tail and negative skewness implies that the distribution has a long left tail [35] [49] . Both fleet capacity and load factor are positively skewed as indicated by the values 0.16 and 0.11 respectively, this means that the mass of the distribution is concentrated on the right. Kurtosis measures the peakedness or flatness of the distribution of the series. Kurtosis is computed as:
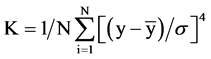 (5)
(5)
where σ is again based on the biased estimator for the variance. The kurtosis of the normal distribution is 3 [35] . If the kurtosis exceeds 3, the distribution is peaked (leptokurtic) relative to the normal; if the kurtosis is less than 3, the distribution is flat (platykurtic) relative to the normal. FLTC is platykurtic as indicated by 1.72, implying that its standard deviation from the mean is large; while load factor is leptokurtic as indicated by the value 3.58 implying that its standard deviation from the mean is small.
4.2. The Nature of Relationships between FLTC and LDFC
This section sought to determine the nature of relationships that existed, as shown by the following scatter diagram, between fleet capacity and load factor.
Figure 1 suggests that fleet capacity and load factor are positively, though weakly, related as indicated by a relatively flatter slope. This implies that as fleet capacity increases, load factor increases but in smaller amounts compared to the increases in fleet capacity. This is supported by [16] ’s finding that reported that in Africa, there was fleet capacity expansion of 5.2% and load factor rose 1.9 percentage for the same year 2013.
4.3. Inferential Analysis
It is well known that many economic time series are difference stationary which produce misleading results,
![]()
Figure 1. Scatter diagram depicting the relationship between fleet capacity and load factor.
Table 9 shows that fleet capacity has an off-the-scale significant positive effect on load factor as indicated by the β = 0.0268 against t-statistic of 4.9837 and a p-value of 0.0000. This implies that any additional 1 seat will result in 0.0268 percentage increase in load factor. The R2 is 0.2276 and the adjusted R2 is 0.2165. The difference between R2 and the adjusted R2 is 0.0112.; and according to [51] , it implies that the model is valid, and has stability for prediction. Thus, the regression accounts for 22.76% of the variance in load factor. This is supported by the fact that the standard deviation of the dependent variable is slightly larger than the standard error of the regression (i.e. 8.6972 is slightly larger than 7.6986%). From these results, the analytic model was developed as follows:
![]() (6)
(6)
where: C represents the individual cross-section fixed effect, and is as follows:
![]()
Table 9. Regression results of the effect of fleet capacity on load factor.
The results imply that, should the low-cost carriers add to its fleet 2 more fifty-seater airplanes, such as a Canadian Royal Jet (CRJ) which form a majority of their fleet, load factor will improve by 3%. This finding supports that of [16] though contradicts [17] . Reference [16] reported that in India, fleet capacity climbed 3.5% in 2013, and load factor was 74.6%, up 1.7 percentage points, while in Africa, there was capacity expansion of 5.2% and load factor rose 1.9 percentage points to 69 percent, indicating that an increase in fleet capacity will result in an increase in load factor. However, [17] found out that fleet capacity is an insignificant negative predictor in explaining the variation in load factor, with a negative coefficient of −1.511. This finding reiterates that when more seats are availed (and this is achieved through increasing the number of airplanes), the availability comes with flexibility in fleet scheduling and management. This ensures more reliability that wins the confidence of the travelling public. Increasing the number of equipment, and consequently the available seats, raises the value of the product to the passenger and increased value leads to higher demand and finally higher load factors. Passengers value the convenience increased capacity provides them. In the end, more bookings are realized which is seen in the form of rising load factor. The finding also implies that unlike in the North America and better part of Europe, Kenya, and to a large extent Africa, still has a segment in her population whose propensity to travel by air can be stimulated through aggressive fare reductions and commercial successes in product designing, promotions, marketing communications, distributions, and service delivery, hence the need to avail more seats.
5. Summary, Conclusions and Recommendations
Correlational analyses indicate that fleet capacity is significantly and positively correlated with load factor; and the study has also established that fleet capacity is a significant positive predictor of load factor. Since airline fleet management and planning requires determining the size of service fleet that is most cost-effective, the study recommends that there is, therefore, a need to identify and adjust accordingly, from time to time, the optimal fleet capacity for their specific operating conditions and environments without under or over supplying the available seats. Airlines management also needs to work on the two key drivers, i.e. pricing and commercial success. This is because fare reductions will generally stimulate demand and commercial success in product design, promotions, marketing communications, distributions, and service delivery will influence load factors. Studies should be designed with a view to replicating the results of this research within the wider setting of the entire Kenyan aviation market to include even the full service carriers.
List of Abbreviations and Acronyms
FFV―Fly540 Aviation Limited
FMOLS―Fully Modified Ordinary Least Squares
LDFC―Load Factor
IATA―International Airlines Transport Association
ICAO―International Civil Aviation Organization
JLX―Jetlink Aviation Limited
FLTC―Fleet Capacity