Triangles Technique for Time and Location Finding of the Lightning Discharge in Spherical Model of the Earth

Anatoliy Lozbin^*, Yuriy Shpadi, Alexander Inchin

Scientific Space Systems Laboratory, Institute of Space Techniques and Technologies, Almaty, Kazakhstan.

DOI: 10.4236/gep.2016.44016                

Abstract

The spherical model of time and location calculation of the lightning discharge is given. The calculations are made by means of radio signals detection by sensors of the distributed network. The full solution of a problem of lightning discharge cloud-ground type location for three sensors is given. Based on this task the lightning location method for a network of sensors was developed. By means of computational experiments, the analysis of accuracy of the model depending on radio signals detection accuracy at observing stations was done.

Keywords

Lightning, Time of Arrival Technique (TOA), Atmospheric, Spherical Trigonometry

Received 15 February 2016; accepted 25 April 2016; published 28 April 2016

1. Introduction

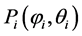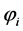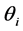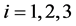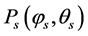Let be 3 different points on the Earth’s surface with longitude and latitude,. In these points, we have sensors receiving a radio signal from lightning discharge. Let there was a lightning discharge in the time moment in some point of the Earth’s surface. Radio signals from this discharge were detected by the sensors in the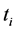, 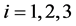time points. Assuming that the radio signal (low frequency) reaches each sensor on the shortest way along an Earth’s surface, we will receive system of three equations for lightning discharge time and location determination.

(1)

where,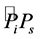―length of a smaller arch of a big circle of the terrestrial sphere connecting points 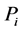and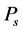,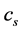―the speed of radio wave.

The system of three Equations (1) is quite defined, as it has three unknown: coordinates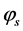, 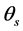and time of discharge.

In a task we believe, that the lightning discharge can occur in any place on Earth surface, that is:

Because of physical sense, timepoint of discharge must happened before all timepoints of its detection on all sensors, that is:

. (2)

On the other hand, the way passed by a radio signal to each sensor can’t be more than length of a semi-circle of a big circle of the Globe. From this follows that

, (3)

where―Earth’s radius. Based on (2) and (3) we conclude that timepoint of the lightning discharge must be in the interval

. (4)

2. System (1) Features

Let is consider some features of the system (1). Using the geocentric coordinate system, which is connected with Earth, we will enter single vectors and hodographs of the points and. Coordinates of the vectors and connected with spherical coordinates of the points and by the equations:

Applying a scalar product of vectors, we can show distance from sensors to a lightning as

. (5)

In geocentric coordinate system the scalar product disclose by the equation:

,

and, in spherical coordinate system:

.

Let’s put (5) into (1) and divide equations on. In result, lead the system (1) to

(6)

where,. The pair, which first component defines location of the lightning discharge, and the second―the moment corresponding to it, is the solution of system (6), if it satisfies to each equation of this system.

We will consider that timepoints are numbered according to increase of their values

. (7)

Otherwise, we will change numbering of points according to (7).

Let’s consider a difference of two equations of system (6)

(8)

For a spherical triangle with vertexes, and which sides located on the same hemisphere, the statement similar to triangles on the plane is fair―the absolute value of a difference of two sides is always less than third side. Thus,

.

From this inequation and (8) it follows that

(9)

The Inequation (9) represents a necessary condition for solvability of the system of Equation (1). Thus, if the difference of the lightning timepoints measured by each couple of sensors does not meet a requirement (9), to define location and time of a lightning discharge based on these sensors it is impossible.

The cause of disarrangement of an Inequation (9) can be in an error of identification of lightning discharges at sensors, or be a consequence of errors of measuring equipment. Further, we believe that the requirement (9) is met.

Geometrically each of the Equation (8) define a set of points on the single sphere. Difference of distances of these points on a sphere surface up to two fixed points and is the constant and equal. Points, and are radial projections of points, and to the single sphere with saving of their spherical coordinates. By analogy with the plane, this set of points is called as a hyperbole. Points and are focuses of a hyperbole. The focal length is equal

, (10)

semi-transverse axis

(11)

Further, we assume that equation in (9) does not exist and the strict in equation we have

(12)

Thereby we exclude a case, when the hyperbole degenerates in an arch interval.

Unlike a flat case, hyperbole on the sphere is the limited closed curve and, moreover, it is coincides with a spherical ellipse. Really, using the identical equation:

let us find

, (13)

where, -is a unit vector opposite vector. Plug (13) into (8), we get an equation:

.

This equation defines a geometrical set of points. The sum of distances of these points on the sphere up to two fixed points and is equal to constant that corresponds to de-

finition of an ellipse on the sphere. Focal length of an ellipse equally, and major semi-axis

. We will notice, that all points of this ellipse are located on a plane limited hemisphere, and this

plane passing through the center of Earth perpendicular to a vector.

The visualization of the Equation (8) given by function graph:

,

which is represented in Figure 1 in a cylindrical rectangular projection. Hyperboles (ellipses) are lines of level of this function. Focuses of all hyperboles are located in points and, which are not marked on graph, but symmetrized on the equator with respect to zero meridian, and the real axes are equal to value of function on the respective level line.

3. Parameterization of a Spherical Hyperbole

Let us find the parametrical equation for a hyperbole (8). Let us add half-plane, which a pass out from vector and can rotate around this vector. We will notice that at any location half-plane has one and only one general point with a hyperbole. This fact is the basis for definition of the parametrical equation of a hyperbole.

Previously we will create orthogonal coordinate system with respect of which there will be a half-plane rotation. To define plane, which vectors and belonging to.

Let us construct a single normal vector to the plane

, (14)

where, is defined by Equation (10), and add vector, believe that

. (15)

, , vectors, chosen in that order are form the right triple of single vectors. vector is a normal to plane, and, , vectors are belonging to this plane. Double vector product expanding we find

. (16)

Thus, the vector is a linear combination of vectors and, and that is natural because of vectors complanarity. Add vector

(17)

Figure 1. Graph of the function. Angle’s values are in degree.

and direct half-plane along this vector. At change angle within 0 to the vector together with half-plane, will make a complete revolution around the axis passing through a vector. Rotation of a vector with increase of the will happen counterclockwise if to look from the end of a vector to the plane of vectors and (positive rotation in unitary vectors, , system).

Thus, the angle is the value, which is defining each point of a hyperbole. Further, we will find relationship between vector and. The vector is within half-plane, therefore it is equal to a linear combination of vectors and,

(18)

where, -is a function of the. The geometrical sense―the it is angle between and vectors. Plugging from (17) into (18) we will get vector resolution by unitary vectors, and.

. (19)

For the finding dependence from we will plug (19) into system of Equation (8). From the Equation (14)-(18) taking to account designations (10)-(11) and features of the vectors multiplication we will find the 3 dot products:

,

,

.

After plugging (19) to (8) we will get an equation

,

which, after arccosines inversion changed to

. (20)

Because of (12), the, then, from (20) we get

,

from this we have

(21)

The Equation (21) give us unknown relationship between and. Then, we will try to find margins change. If the

,

if the

Therefore, values are satisfy of the equation

. (22)

By using sine and cosine of the angle through cot, we will get:

. (23)

Thus, the required parametrical equation for a hyperbole (8) is set by Equation (19) in which value is defined by equation (21) or is from the Equation (23).

4. The System (1) Solving

By excluding 1st equation from 2nd and 3rd in (6) we will get equivalent system:

(24)

Two last equations describe two hyperboles, which have the general focus set by vector. Thereof, the parametrical Equation (19) of these hyperboles can be reduced to one parameter. For this purpose, it is necessary to combine rotation of half-planes and, which proceed from the same axis set by a vector and define the position of the current points on the first and second hyperboles. As a result, two parametrical equations of hyperboles depending on one general value we have. A point of intersection of hyperboles will define the position of a lightning discharge. We will give the corresponding formulas.

Parametrical equation of the 2nd equation in the system (24):

, (25)

where,

, ,

,

Parametrical equation of the 3rd equation in the system (24):

, (26)

where,

, ,

,

At the same values and the angle between half-planes and is equal to angle between vectors and, i.e.

. (27)

Let the vectors, , are right, so their scalar triple product is positive,

. (28)

Then, at the half-planes and coupling the angle with any values will be exceed on the constant, so the Equation (29) will be right

. (29)

If the scalar triple product of the vectors, иis negative, for reduction to an Inequation (28) it is enough to change numbering of vectors and in system (24).

By plugging (29) in (26), we will receive the parametrical equations of two hyperboles, which depend on one parameter.

Vectors and in a point of intersection of hyperboles must be coincide. In order that and were equal, the equality of angles and is necessary and sufficient. As these angles are defined inside interval on which the cot branch is also defined, then cot of these angles are equal,

.

By plugging cot values, we will get equation relative to

. (30)

By identical transformations, the Equation (30) will be as

,

where,

,

,

.

Believe that

we get equation:

, (31)

where,.

Depending on value three cases are possible:

1) If, then hyperboles are crossed in two points

2) If, then hyperboles have one general point

,

3) If, then hyperboles have no general point and the task of lightning position definition has no solutions.

After finding the is calculated and then vector, defining the position of a lightning discharge. The vector in a point of a lightning discharge coincides with a vector.

To lightning discharge there can correspond only one point of intersection of hyperboles, which we will call actual. The second point is a consequence of crossing of two closed convex curves leaning at each other. This point we will call phantom.

Timepoints of both lightning discharges (actual and phantom) are defines by formula (32), which is develop from the first equation of system (28):

. (32)

Thus, if the lightning detection network consists only of three sensors, then with conditions (12) keeping we have actual position of a lightning and, as a rule, there is a phantom point.

For system of the Equation (24) both of its solutions are equal. Therefore, to allocate a lightning actual point, additional information is necessary. For example, for this purpose it is possible to use a vector of induction of a magnetic component of the accepted radio signal of a lightning which coordinates can be received by means of the bidirectional magnetic antenna [1] [2] . However, as appears from the analysis of the Equation (31), in some situations depending on mutual position of sensors and lightning discharge, positions of the actual and phantom signals can be very close that does a problem with real signal separation.

5. Example

In a demonstration example, three measurement points which are conditionally placed near the cities of Almaty, Taldykorgan and Kapshagay (Republic of Kazakhstan) were selected. The corresponding timepoints are calculated in the assumption that the lightning discharge occurred near Astana city. Zero was taken for initial counting of time. Given data for calculation are presented in Table 1. In test calculation of discharge time in the task solution, the following values were taken:

Speed of radio waves―299,792.458 km/s,

Average Earth radius―6371.308 km.

As a result of the task solution, two points of the lightning discharge with various timepoints of a discharge are defined. Results of calculation are given in Table 2.

Parameters of the actual and phantom points of the lightning discharge are mutually reversible. That is, if according to a phantom point, provided in Table 2 to define time of registration of the lightning discharge and to make calculation of a lightning discharge, then we will receive the same results given in Table 2.

Lightning discharge location and timepoint in a phantom point are displaced with respect to actual.

6. Triangles Technique Application for Timepoint and Location of the Lightning Discharge for Set of Sensors

Let’s consider a set of N sensors located randomly on the Earth’s surface in the points, ,. Let in point there was a lightning discharge the signal from which reaches each station in moment.

We will put in compliance to each point a unit vector of its hodograph and point of lightning discharge -unit vector. In this case, the system (11) will expand to N

Table 1. Sensors locations and timepoints of the lightning discharge detection.

Table 2. Calculation results.

equations

(33)

We will make subsystems from the equations of system (33), including three equations to each subsystem. We will call such subsystems as triads. In total, it is possible to make M triads from N equations, where

Let each triad of the Equation (33) have two solutions. We will construct the set of solutions, of all triads and calculate functional values on each solution.

(34)

If the functional at any solution will become zero (it is possible with given accuracy), then this pair will be a system (33) solution.

If at any solution, then, for approximate solution of the system (33) we choose solution, where functional has lower values. Without losing a generality, we will suppose, that.

For an assessment of the received solution of system (33) we will allocate the subset including the M actual solutions from a set of all solutions of triads. For this purpose we use the natural assumption, that on the actual solution the functional have lesser value, than on phantom solution (in case of three sensors these values coincide and both are equal to zero). If both solutions of some triads are close to each other, then, in rare cases, this assumption can be violated. We will number this subset values as.

We will determine an arithmetic average value on a subset of actual solutions

(35)

For the accuracy ranking of the approximation at the position of the lightning discharge we take a distance between

, (36)

and at time-difference

. (37)

The grade of dispersion of intersection points of hyperboles is characterized by an average square deviation from the position of the solution, which is calculated by formula

. (38)

For the analysis of the given technique a number of numerical experiments was executed. In all experiments the same group of 6 sensors with coordinates are given in Table 3 was used.

Numerical experiments are given for three points of a lightning placed in various regions of Kazakhstan, removed from each other―in the North, West and East. For each lightning coordinates are set and conditionally exact time of detection within 1ps accuracy is calculated. The zero moment of each lightning discharge in each experiment is taking. Lightning parameters are given in Table 4. In addition, for the subsequent analysis the distance from stations to a point of the lightning is specified in Table 4.

The problem of each experiment consisted in lightning position and initial moment calculation with triangles technique depending on the accuracy of lightning detection on stations. Time of lightning detection was set by rounding of exact values of the moments of detection given in Table 4 by step-by-step approximation to 1 ns, 10 ns, 100 ns and 1 μs. Results of calculations are given in Tables 5-7.

Table 3. Sensors location.

Table 4. Lightning discharge parameters.

Table 5. The results of experiment for lightning in Astana city region (51˚N, 71˚E).

Table 6. The results of experiment for lightning in Aktau city region (44˚N, 51˚E).

Table 7. The results of experiment for lightning in Zaisan city region (47˚N, 85˚E).

7. Conclusion

Comparing change of result of lightning discharge time and location calculation on ratio of increase of an error of lightning detection time, it is possible to make a conclusion that the presented technique of calculation is effective and reliable if the detection accuracy does not exceed 100 nanoseconds. Since the accuracy of 1 microsecond range of hyperboles intersection points dispersion for different triads which is characterized by increase in distance between them and accident of their mutual position considerably increases.

Acknowledgements

The work is supported by the Grant 0100/GF4 of Ministry of Education and Science of the Republic of Kazakhstan.

Conflicts of Interest

The authors declare no conflicts of interest.

References

[1]	Koshak, W.J. and Solakiewicz, R.J. (2001) TOA Lightning Location Retrieval on Spherical and Oblate Spheroidal Earth Geometries. Journal of Atmospheric and Oceanic Technology, 18, 187-199. http://dx.doi.org/10.1175/1520-0426(2001)018<0187:TLLROS>2.0.CO;2
[2]	Kuterin, F.A., Bulatov, A.A. and Shlyugaev, Yu.V. (2014) The Development of the Lightning Detection Network Based on BoltekStormTracker Hardware. XV International Conference on Atmospheric Electricity, Norman, 15-20 June 2014, 71-74.