Representations by Certain Sextenary Quadratic Forms Whose Coefficients Are 1, 2, 3 and 6 ()
Received 9 December 2015; accepted 26 March 2016; published 29 March 2016

1. Introduction
The divisor function 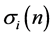 is defined for a positive integer i by
is defined for a positive integer i by
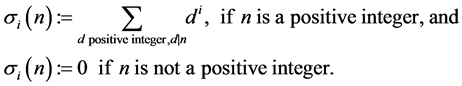
The Dedekind eta function and the theta function are defined by
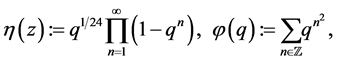
where

and an eta quotient of level N is defined by
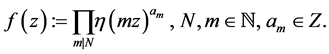 (1)
(1)
It is important and interesting to determine explicit formulas of the representation number of positive definite quadratic forms.
Here we give the following Lemma, see ( [1] , Theorem 1.64), about the modularity of an eta quotient.
Lemma 1. An eta quotient of level N is a meromorphic modular form of weight 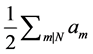 on
on 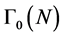 having rational coefficients with respect to q if
having rational coefficients with respect to q if
a) 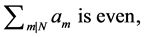
b) 
c) 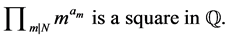
For 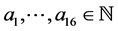 and a nonnegative integer n, we define
and a nonnegative integer n, we define
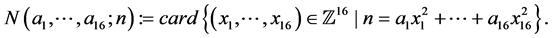
Clearly 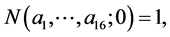 and without loss of generality we can assume that
and without loss of generality we can assume that 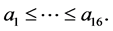
Now, let’s consider sextenary quadratic forms of the form
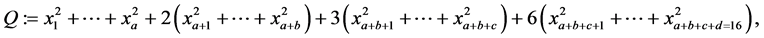
where![]() ,
,![]()
We write ![]() to denote the number of representations of n by a sextenary quadratic form
to denote the number of representations of n by a sextenary quadratic form![]() . Its theta function is obviously
. Its theta function is obviously
![]()
Formulae for ![]() for the nine octonary quadratic forms (2i, 2j, 2k, 2l) = (8, 0, 0, 0), (2, 6, 0, 0), (4, 4, 0, 0), (6, 2, 0, 0), (2, 0, 6, 0), (4, 0, 4, 0), (6, 0, 2, 0), (4, 0, 0, 4), and (0, 4, 4, 0) appear in the literature, (cf. [2] - [12] ). Alaca and Williams have obtained some results on sextenary quadratic forms in terms of the functions
for the nine octonary quadratic forms (2i, 2j, 2k, 2l) = (8, 0, 0, 0), (2, 6, 0, 0), (4, 4, 0, 0), (6, 2, 0, 0), (2, 0, 6, 0), (4, 0, 4, 0), (6, 0, 2, 0), (4, 0, 0, 4), and (0, 4, 4, 0) appear in the literature, (cf. [2] - [12] ). Alaca and Williams have obtained some results on sextenary quadratic forms in terms of the functions ![]() and
and![]() , see [13] [14] . There are more works on representation number of sextenary quadratic forms in [15] - [17] . Other methods for representation number have been used in (cf. [7] [10] [12] [18] [19] ). Here, we will classify all fourtuples
, see [13] [14] . There are more works on representation number of sextenary quadratic forms in [15] - [17] . Other methods for representation number have been used in (cf. [7] [10] [12] [18] [19] ). Here, we will classify all fourtuples ![]() for which
for which ![]() is a modular form of weight 8 with level 24. Then we will obtain their representation numbers in terms of the coefficients of Eisenstein series and some eta quotients.
is a modular form of weight 8 with level 24. Then we will obtain their representation numbers in terms of the coefficients of Eisenstein series and some eta quotients.
First, by the following Theorem, we characterize the facts that
![]()
are in ![]()
Theorem 1. Let
![]()
where, ![]() ,
,![]() be a sextenary quadratic form. Then its theta series is of the form
be a sextenary quadratic form. Then its theta series is of the form
![]()
Moreover, it is in ![]() if and only if
if and only if ![]() is given in the Table 1. Here we also see that
is given in the Table 1. Here we also see that ![]() are either both even or both odd.
are either both even or both odd.
Proof. It follows from the Lemma 1, holomorphicity criterion in ( [20] Corollary 2.3, p. 37) and the fact
that
![]()
The condition ![]() is a square of a rational number implies that either
is a square of a rational number implies that either ![]() are both even or both odd integers.
are both even or both odd integers.
Now let,
![]()
![]()
![]()
![]()
![]() the unique newform in
the unique newform in ![]()
![]()
![]()
![]()
![]()
![]()
![]()
Theorem 2. The set
![]()
is a basis of![]() . Moreover, the unique newform in
. Moreover, the unique newform in ![]() is
is![]() , the unique newform in
, the unique newform in ![]() is
is![]() , the two unique newforms in
, the two unique newforms in ![]() are
are
![]()
![]()
the two unique newforms in ![]() are
are
![]()
![]()
and the three unique newforms in ![]() are
are
![]()
![]()
![]()
Proof. ![]() is 32 dimensional,
is 32 dimensional, ![]() is 24 dimensional, see ( [21] Chapter 3, p. 87 and Chapter 5, p. 197), and generated by
is 24 dimensional, see ( [21] Chapter 3, p. 87 and Chapter 5, p. 197), and generated by
![]()
![]()
![]()
![]()
![]()
![]()
where ![]() is the unique newform in
is the unique newform in![]() ;
; ![]() is the unique newform in
is the unique newform in![]() ;
; ![]() is the unique newform in
is the unique newform in![]() ,
, ![]() are the unique newforms in
are the unique newforms in![]() ;
; ![]() are the unique newforms in
are the unique newforms in ![]() and
and ![]() are the unique newforms in
are the unique newforms in![]() .
.
As a consequence of this Theorem, we have obtained the following Corollary.We have used Magma for the calculations.
2. Corollary
The following representation numbers formulae are valid.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()