An Independence Property for General Information

Doretta Vivona, Maria Divari

Department of Basic and Applied Sciences for Engineering, Faculty of Civil and Industrial Engineering, “Sapienza”—University of Rome, Roma, Italy.

DOI: 10.4236/ns.2016.82008                

Abstract

The aim of this paper was a generalization of independence property proposed by J. Kampé de Feriét and B. Forte in Information Theory without probability, called general information. Therefore, its application to fuzzy sets has been presented.

Keywords

Information, Functional Equations, Fuzzy Sets

Received 25 December 2015; accepted 19 February 2016; published 22 February 2016

1. Introduction

Since 1967-69, J. Kampé de Ferét and B. Forte have introduced, by axiomatic way, new information measures without probability [1] - [3] ; later, in analogous way, with P. Benvenuti we have defined information measures without probability or fuzzy measure [4] for fuzzy sets [5] [6] . This form of information measure is again called general information.

In Information Theory an important role has played by an independence property with respect to a given information measures J applied to crisp sets [7] . These sets are called J-independent (i.e. independent each other with the respect to J) [8] .

For this reason we will propose a generalization of J-independence property.

The paper develops in the following way: in Section 2 we recall some preliminaires; in Section 3 the generalization of J-indepedence is proposed; the result is extended to fuzzy sets in Section 4. Section 5 is devoted to the conclusion.

2. Preliminaires

J. Kampé de Ferét and B. Forte gave the following definition [1] [2] :

Definition 2.1 Measure of general information J for crisp sets is a mapping

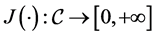
such that: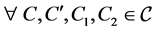

(i)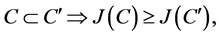

(ii)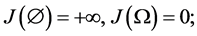

(iii)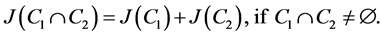

If the couple 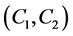satisfies the (iii), we say that 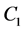and 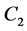are J-independent, i.e. independent each other with respect to information J.

3. A Generalization of the J-Independence Property

In this paragraph we are going to present a generalization of the J-independence property.

We propose the following:

Definition 3.1 Given a general information J, let and be two crisp sets in C such that 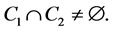We say that and are J-idependent each other if there exists a continuous function such that

(1)

We shall characterize the function, taking into account the properties of the intersection for every:

Putting the properties [(p₁) - (p₅)] have translated in the fol- lowing system of functional equations and inequalities [9] [10] :

We can give the following

Proposition 3.2 A class of solutions of the system [(P₁) - (P₅)] is

(2)

where h is any continuous, strictly increasing function with and

Proof. The class of functions (2) satisfy the equations [(P₁)-(P₃)] and the inequality (P₄) by appling the Ling Theorem about the representation of a function which is monotone, commutative, associative with neutral element [11] . The inequality (P₅) is a consequence of the monotonicity of h.

So, from (2), we have

Proposition 3.3 The generalization of the J-independence property for crisp sets is

(3)

where h is any continuous, strictly increasing function with and

Remark When h is linear, the generalization (3) coincide with the property (iii).

4. Extension to Fuzzy Setting

In this paragraph, we are considering the extension of J-independence property at fuzzy setting.

Definition 4.1 Measure of general information in fuzzy setting is a mapping such that:

(i')

(ii')

(iii')

If the couple satisfies the (iii'), we say that and are J'-independent, i.e. independent each other with respect to information.

Also in fuzzy setting, we generalize the (iii'), setting

(4)

The properties of the intersection between fuzzy sets are the similar to the [(p₁) − (p₄)] [5] [6] . Therefore, we are looking for functions (4) solutions of the system [(P₁) − (P₅)]. We have again the similar result:

Proposition 4.2 A class of solution of the system [(P₁) − (P₅)] is

(5)

where k is any continuous, strictly increasing function with and

From (5), we get

Proposition 4.3 A generalization of the J'-independence property between two fuzzy set is

(6)

where k is any continuous, strictly increasing function with and

Proof. The proof is similar to that given for crisp sets.

Remark. When k is linear, the generalization (6) coincide with the property (iii').

5. Conclusions

In this paper we have proposed a genralization of J-independence property between crisp sets:

where h is any continuous, strictly increasing function with and

Therefore, we have extended the result to fuzzy setting:

where k is any continuous, strictly increasing function with and

Conflicts of Interest

The authors declare no conflicts of interest.

References

[1]	Kampé de Fériet, J. and Forte, B. (1967) Information et Probabilité. Comptes Rendus de l’Académie des Sciences Paris, 265, 110-114, 142-146, 350-353.
[2]	Forte, B. (1969) Measures of Information: The General Axiomatic Theory. RAIRO Informatique Théorique et Applications, 63-90.
[3]	Kampé de Feriét, J. (1970) Mesures de l'information fornie par un evénement. Colloque International du Centre National de la Recherche Scientifique, 186, 191-221.
[4]	Benvenuti, P., Vivona, D. and Divari, M. (1990) A General Information for Fuzzy Sets. Uncertainty in Knowledge Bases, Lectures Notes in Computer Sciences, 521, 307-316. http://dx.doi.org/10.1007/BFb0028117
[5]	Zadeh, L.A. (1965) Fuzzy Sets. Information and Control, 8, 338-353. http://dx.doi.org/10.1016/S0019-9958(65)90241-X
[6]	Klir, G.J. and Folger, T.A. (1988) Fuzzy Sets, Uncertainty and Information. Prentice-Hall International Editions, Englewood Cliffs.
[7]	Halmos, P.R. (1965) Measure Theory. Van Nostrand Company, Princeton.
[8]	Benvenuti, P. (2004) L’opera scientifica. Roma, Ed.Univ.La Sapienza, Italia.
[9]	Aczél, J. (1966) Lectures on Functional Equations and Their Applications. Academic Press, New York.
[10]	Forte, B. (1970) Functional Equations in Generalized Information Theory. In: Applications of Functional Equations and Inequalities to Information Theory, Ed. Cremonese, Roma-Italy, 113-140.
[11]	Ling, C.-H. (1995) Representation of Associative Functions. Publicationes Mathematicae, 12, 189-212.