Necessary Optimality Conditions for Multi-Objective Semi-Infinite Variational Problem

Bharti Sharma¹, Promila Kumar²

¹Department of Mathematics, University of Delhi, New Delhi, India.
²Department of Mathematics, Gargi College, University of Delhi, New Delhi, India.

DOI: 10.4236/ajor.2016.61006                

Abstract

In this paper, necessary optimality conditions for a class of Semi-infinite Variational Problems are established which are further generalized to a class of Multi-objective Semi-Infinite Variational Problems. These conditions are responsible for the development of duality theory which is an extremely important feature for any class of problems, but the literature available so far lacks these necessary optimality conditions for the stated problem. A lemma is also proved to find the topological dual of  as it is required to prove the desired result.

Keywords

Semi-Infinite, Variational Problem, Efficient Solution, Necessary Optimality Conditions

Received 30 November 2015; accepted 18 January 2015; published 22 January 2016

1. Introduction

A Semi-infinite Programming Problem (SIP) [1] -[3] is an optimization problem in which the index set of inequality constraints is an arbitrary and not necessarily finite set. It has wide variety of applications in various fields like economics, engineering, mathematical physics and robotics. While browsing the literature, we observe that much attention has been paid to SIP which is static in nature in the sense that time does not enter into consideration. Whereas in practical problems we come across situations where time plays an important role and hence cannot be neglected.

Semi-infinite Programming Problem is tightly interwoven with Variational Problem [4] -[9] . Both these subjects have undergone independent development, hence mutual adaptation of ideas and techniques have always been appreciated.

In this article, we propose Semi-infinite Variational Problem for which necessary optimality conditions are established. These optimality conditions are further extended to Multi-objective Semi-infinite Variational Problem (MSVP). We also clarify, with proper reasoning, certain points which were left for later validation in [9] .

Necessary optimality conditions are important because these conditions lay down foundation for many computational techniques in optimization problems as they indicate when a feasible point is not optimal. At the same time these conditions are useful in the development of numerical algorithms for solving certain optimization problems. Further, these conditions are also responsible for the development of duality theory on which there exists an extensive literature and a substantial use of which (duality theory) has been made in theoretical as well as computational applications in many diverse fields. While browsing the literature, we found that necessary optimality conditions were not proved for the class of semi-infinite variational problems.

The paper is organized as follows: In section 2 some basic definitions and preliminaries are given. Section 3 deals with necessary optimality conditions for semi-infinite variational problem; single objective as well as multi- objective. In section 4, we prove a lemma which is required to prove necessary optimality conditions of section 3, for semi-infinite variational problem.

2. Definitions and Preliminaries

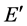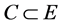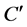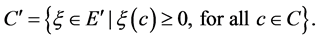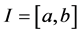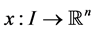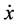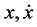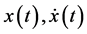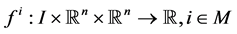Let E be a topological vector space over the field of real numbers and denotes the topological dual space of E. For a set, the topological polar cone of C is Let r and n be two positive integers. For a given real interval, let be a piecewise smooth state function with its derivative. For notational convenience we write in place of. Let, and 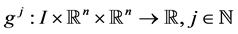be continuously differentiable functions with respect to each of their argument. We also denote the partial derivative of 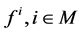with respect to 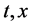and by respectively. Analogously, we write the partial derivative of. For the sake of notational convenience we write for and for for.

For any, in n-dimensional Euclidean space,

1) for all

2) for all

3) for all

4) and

Let and denote the non negative and positive orthant of respectively. Let X be the space of piecewise smooth state functions which equipped with the norm, where the differential operator D is given by

Therefore, except at discontinuities.

Consider the following Multi-objective Semi-infinite Variational Problem (MSVP):

subject to

(1)

(2)

with the norm defined as above is a Banach space.

Let be the set of all feasible solutions of (MSVP).

Definition 1 A point is said to be an efficient solution for (MSVP) if there is no other such that

3. Necessary Optimality Conditions

Let us first prove necessary optimality conditions for the following single objective Semi-infinite Variational Problem (SVP):

subject to

(3)

(4)

where is continuously differentiable function with respect to each of its argument.

The problem (SVP) may be rewritten as Cone Constrained Problem (CCP):

subject to

(5)

where is defined as

(6)

where is Lebesgue measure.

is defined as

(7)

Theorem 2 Let be an optimal solution of (SVP). Then there exist and piecewise smooth functions for finitely many such that

(8)

(9)

(10)

Proof. Since is an optimal solution of (SVP), so is of (CCP). Therefore there exist and

(topological polar cone of K) [10] such that

(11)

(12)

where and are Frechet derivatives of and G at.

Also for every,

(13)

(14)

Since,

By Lemma 1 (proved in Section 4)

Let For by Riesz representation theorem [11] there exist

such that

(15)

for, choose, therefore for any,

(16)

Substituting in (16) and using (12), we arrive at (9).

Now it follows from (11)

(17)

(13) along with (16) implies

(18)

On using (14), we get

(19)

(20)

Integrating by parts the following function and using boundary condition of h,

(21)

Using above equation in (20), we get

(22)

By fundamental theorem of calculus of variation [12]

(23)

Claim 1:

Without loss of generality assume that

Since,

(24)

(25)

In particular

(26)

Claim 2:, where

Let if possible, then

Define

Then but a contradiction.

Hence Claim 2 holds, that is,

Using the same argument Hence claim 1 also holds.

The relations (16) are generally valid only if is Schwarz distribution. Condition (8) is a

linear first order differential equation for, therefore for given, equation (8) is solvable for piecewise smooth function [9] [13] .

Theorem 3 (Necessary Optimality Conditions) Let be a normal efficient solution for (MSVP). Then there exist and piecewise smooth functions for finitely many such that the following conditions hold:

(27)

(28)

(29)

Proof. This theorem can be proved by using Theorem 2 and proceeding on the similar lines of ([14] , Theorem 3.4).

The following example illustrates the validity of Theorem 3.

Example 4 Consider the problem (P1):

Subject to

(30)

(31)

where is a piecewise smooth state function. It is trivial that is a normal efficient solution for (P1). It can be verified that there exist and smooth functions for such that (27), (28) and (29) hold.

The following example illustrates that a feasible solution of (MSVP) fails to be a normal efficient solution if it does not satisfy any one of the necessary optimality conditions (27), (28) or (29).

Example 5 Consider the problem (P2):

Subject to

(32)

(33)

where is a piecewise smooth state function. Then is feasible solution for (P2). But not a normal efficient solution, since it not satisfied condition (27) for any and for any piecewise smooth functions for finitely many

4. Topological Dual of

Let us summarizes some basic concepts and tools to find topological dual of.

1) is a Riesz space ([15] , p. 313) as it is partially ordered by the pointwise ordering in if and only if in, for each. Its lattice operations are given pointwise

(34)

(35)

2) is also a Riesz space.

3) Order dual of is a Riesz space ( [15] , Theorem 8.24).

4) is a Frechet lattice, as it is Banach lattice ([15] , p. 348). Since countable cartesian product of Frechet lattice is Frechet lattice ( [16] , Theorem 5.18) which imply is Frechet lattice equipped with the product topology.

5) Given define the n-tail of by

(36)

Motivated by the topological dual of ([15] , Theorem 16.3), we now find the topological dual of in the following lemma.

Lemma 1 The topological dual of is

Proof. For any, define,

(37)

Clearly is a continuous linear functional on.

For the converse, assume that is continuous linear functional. The continuity of at zero element of guarantees that there exist and such that and for imply.

So for each for each n, hence.

For each define as

(38)

Then is a continuous linear functional.

By Riesz representation theorem, for there exist such that

(39)

Now let

note that for each

That is and h is uniquely determined.

Now, if then, for all

Conversely, proceeding similarly as in claim 1 of Theorem 2, it can be shown that

if, for all then.

This infers is a lattice isomorphism from D onto.

Hence ([15] , Theorem 9.11).

5. Conclusion

In this paper, we have developed necessary optimality conditions for a Semi-Infinite Variational Problem. These optimality conditions are further extended to Multi-objective Semi-infinite Variational Problem (MSVP) as Theorem 3. The results proved in this article are significant for the growth of optimality and duality theory for the class of semi-infinite variational problems. An example is presented to demonstrate the validity of the theorem proved. Another example illustrates that a feasible solution of (MSVP) fails to be a normal efficient solution if it does not satisfy any one of the necessary optimality conditions stated in the theorem. Vital part of the result depends on the topological dual of which was proved as a lemma in the last section.

Acknowledgements

We thank the Editor and the referee for their comments. The first author was supported by Council of Scientific and Industrial Research, Junior Research Fellowship, India (Grant no 09/045(1350)/2014-EMR-1).

Conflicts of Interest

The authors declare no conflicts of interest.

References

[1]	Lopez, M. and Still, G. (2007) Semi-Infinite Programming. European Journal of Operational Research, 180, 491-518. http://dx.doi.org/10.1016/j.ejor.2006.08.045
[2]	Kanzi, N. and Nobakhtian, S. (2010) Optimality Conditions for Non-Smooth Semi-Infinite Programming. Optimization, 59, 717-727. http://dx.doi.org/10.1080/02331930802434823
[3]	Mishra, S.K., Jaiswal, M. and An, L.T.H. (2012) Duality for Nonsmooth Semi-Infinite Programming Problems. Optimization Letters, 6, 261-271. http://dx.doi.org/10.1007/s11590-010-0240-8
[4]	Mond, B. and Hanson, M.A. (1967) Duality for Variational Problems. Journal of Mathematical Analysis and Applications, 18, 355-364. http://dx.doi.org/10.1016/0022-247x(67)90063-7
[5]	Hanson, M.A. (1964) Bounds for Functionally Convex Optimal Control Problems. Journal of Mathematical Analysis and Applications, 8, 84-89. http://dx.doi.org/10.1016/0022-247x(64)90086-1
[6]	Bhatia, D. and Kumar, P. (1996) Duality for Variational Problems with B-Vex Functions. Optimization, 36, 347-360. http://dx.doi.org/10.1080/02331939608844189
[7]	Bhatia, D. and Mehra, A. (1999) Optimality Conditions and Duality for Multiobjective Variational Problems with Generalized B-Invexity. Journal of Mathematical Analysis and Applications, 234, 341-360. http://dx.doi.org/10.1006/jmaa.1998.6256
[8]	Antczak, T. (2014) On Efficiency and Mixed Duality for a New Class of Nonconvex Multiobjective Variational Control Problems. Journal of Global optimization, 59, 757-785. http://dx.doi.org/10.1007/s10898-013-0092-8
[9]	Husain, I. and Jabeen, Z. (2005) On Variational Problems Involving Higher Order Derivatives. Journal of Applied Mathematics and Computing, 17, 433-455. http://dx.doi.org/10.1007/BF02936067
[10]	Luc, D.T. (1989) Theory of Vector Optimization, Lecture Notes in Economics and Mathematical Systems, Vol. 319. Springer-Verlag, New York, 75.
[11]	Kreyszig, E. (1989) Introductory Functional Analysis with Applications. Wiley Classics Library, Wiley, New York, 188.
[12]	Gelfand, I.M. and Fomin, S.V. (1963) Calculas of Variations. Prentice-Hall, Inc., Englewood Cliffs, 34-35.
[13]	Chandra, S., Craven, B.D. and Husain, I. (1985) A Class of Non-Differentiable Continuous Programming Problems. Journal of Mathematical Analysis and Applications, 107, 122-131. http://dx.doi.org/10.1016/0022-247X(85)90357-9
[14]	Mititelu, S. and Stancu-Minasian, I.M. (2009) Efficiency and Duality for Multiobjective Fractional Variational Problems with (ρ,b)-Quasiinvexity. Yugoslav Journal of Operations Research, 19, 85-99. http://dx.doi.org/10.2298/yjor0901085m
[15]	Aliprantis, C.D. and Border, K.C. (1999) Infinite Dimensional Analysis, A Hitchhiker’s Guide. Springer-Verlag, Berlin Herdelberg, 313, 324, 348, 352, 528. http://dx.doi.org/10.1007/978-3-662-03961-8
[16]	Aliprantis, C.D. and Burkinshaw, O. (2003) Locally Solid Riesz Spaces with Applications to Economics. American Mathematical Society, Providence, 127. http://dx.doi.org/10.1090/surv/105