Revealed Cores: Characterizations and Structure

Stefano Vannucci

Department of Economics and Statistics, University of Siena, Siena, Italy.

DOI: 10.4236/am.2015.614200                

Abstract

Characterizations of the classes of all choice functions that select the cores or the externally stable cores induced by an underlying revealed dominance digraph are provided. Relying on such characterizations, the basic order-theoretic structure of the corresponding sets of revealed cores is also analyzed. In particular, it is shown that the poset of all revealed cores ordered by set inclusion is a median meet semilattice: therefore, any profile of revealed cores may be aggregated by means of the simple majority rule.

Keywords

Core, Choice Functions, Dominance Digraphs, Revealed Preference

Received 30 September 2015; accepted 27 December 2015; published 30 December 2015

1. Introduction

The core of a game is the set of its undominated outcomes, with respect to a suitably defined dominance irreflexive relation, or loopless digraph. Now, consider the ongoing operation of a multi-agent system, e.g. an organization or indeed any decision-making unit whose outputs are aptly modeled as the outcomes of a game. Let us then assume that the set of available options does in fact change at a faster pace than the behavioural attitudes of the relevant players and the latter interact as predicted by the core of that game. It follows that the corresponding choice behaviour of the given interaction system as recorded by its choice function should be constrained in some way by its game-theoretic structure and thus somehow reveal that fact. But then, what are the characteristic “fingerprints” of such a choice function, namely the testable behavioural predictions of the core as a solution concept? Or more simply, which choice functions defined over arbitrary subsets of an “universal” outcome set may be regarded as revealed cores? Let us call that issue, for ease of reference, the (full domain) core revelation problem.

Apparently, such a problem has never been addressed in its full generality in the extant literature. To be sure, parts of the massive body of literature on “revealed preference” provide partial answers addressing the case of nonempty cores, i.e. of acyclic revealed dominance digraphs (see e.g. [1] -[4] ). Moreover, there is also some work covering the case of possibly empty sets of undominated outcomes for an arbitrary―i.e. possibly not irreflexive-binary relation R, hence putting aside the original game-theoretic interpretation of R as a dominance relation (see e.g. [5] , and [6] ). But of course the dominance relation of a game in its usual meaning has to be irreflexive (no outcome dominates itself), and the core of a game may well be empty, because its revealed dominance digraph may have cycles. Here, we are interested precisely in the general version of the core revelation problem for the full domain, namely in a characterization of all revealed cores as solutions for a certain “universal” outcome set and all of its subsets, including (locally) empty-valued cores.

The present paper is aimed at filling this gap in the literature by addressing the general core revelation problem with full domain as formulated above. It contributes to the extant literature in the following ways:

・ it provides characterizations of all choice functions with full domain―proper or not―that represent revealed cores,

・ under several variants of the notion of core (Theorems 7, 10, and 14).

Moreover,

・ A study of the basic order-theoretic structure of the corresponding classes of revealed core-solutions as canonically ordered by set-inclusion is also provided (Theorems 17, 20, 21 and 22). In particular, it is shown that the class of all revealed cores (as opposed to, say, the class of nonempty-valued revealed cores) is a meet sub-semilattice of the lattice of all choice functions, and in fact a median meet semilattice (see Theorem 17). A remarkable consequence of that fact is that any profile of revealed cores is amenable to aggregation by the simple majority rule.

Thus, it turns out that each revealed core embodies a considerable part of standard maximizing choice, while the global structure of (full domain) revealed cores retains the order-theoretic properties of the space of all (full domain) choice functions that is most significant from the point of view of simple majority aggregation.

A further generalization of the core revelation problem to the case of choice functions with an arbitrary domain (along the lines of [6] ) would be most helpful. That task is left as a topic for another paper.

The paper is organized as follows: Section 2 includes a presentation of the model and the main characterization results; Section 3 provides some basic results concerning the order-theoretic properties of the classes of revealed core-solutions previously characterized; Section 4 consists of a few concluding remarks.

2. Choice Functions and Revealed Cores

Let X be a set denoting the “universal” outcome set, with cardinality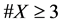, and 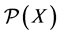its power set. It is also assumed for the sake of convenience that X is finite (but it should be remarked that the bulk of the ensuing analysis is easily lifted with suitable minor adaptations to the case of an infinite outcome set). A choice function on X (with full domain) is a deflationary operator on 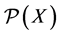i.e. a function 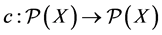such that 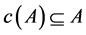for any 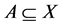(empty choice sets are allowed). A choice function c is proper if 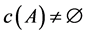when- ever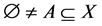. We denote C_X the set of all choice functions on X, and 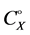the subset of all proper choice functions on X. The proper subdomain of 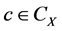-written D_c-is the set of all subsets of X with a nonempty-va- lued choice set i.e.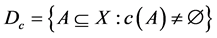. For any binary relation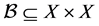, and any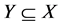, 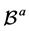and 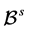denote the asymmetric and symmetric components of, respectively, while and. Recall that is reflexive iff for all, irreflexive iff not for all, total iff or for any, asymmetric iff entails not for any, transitive iff and entail for any, quasi-transitive if is transitive, negatively transitive if is transitive. The transitive closure is the smallest transitive. Moreover, is strictly acyclic iff its transitive closure is irreflexive, and a strict partial order iff it is both asymmetric and transitive.

Let be an irreflexive binary relation on X, denoting a suitably defined dominance relation: is the corresponding dominance digraph. In particular, is asymmetric if.

For any, denotes the dominance relation induced by Δ on Y (of course), and is the induced dominance subdigraph on Y. Broadly speaking, the core of is the set of -undominated outcomes in Y, namely

.

The a-core of is the set of -undominated outcomes in Y, namely

.

The core (a-core) of is externally stable iff for any there exists such that (for any there exists such that, respectively).

A dominance digraph is also said to be core-perfect or strictly acyclic (acyclic, respectively) if (, respectively) for any.

Remark 1. It should be emphasized here that any dominance digraph may arise in a natural way from an underlying game in coalitional form and from a related game in strategic form. Indeed, the dominance digraph

defined by the following rule can be attached in a natural way to any coalitional game

:

For any, , iff there exist and such that and for all and (see [7] for further details).

Two binary relations, R_c induced by a choice function on X and defined as follows will play a pivotal role in the ensuing analysis: for any, if and only if, while if and only if there exists such that and.

A choice function is a revealed core-solution if there exists an irreflexive relation such that for any. Similarly, is a revealed a-core-solution (ES core-solution, ES a-core-solution, respectively) if there exists an irreflexive relation such that (with externally stable, , , respectively) for any. Then, we also say that c is core-rationalizable (a-core-rationalizable, ES-core-rationalizable, ES-a-core-rationalizable respectively) by the dominance digraph. Clearly, ES (a-)core-solutions are refinements of (a-)core solutions. Revealed cores will also be used as a generic label to denote all the foregoing choice functions.

The following choice functions provide some remarkable examples―and non-examples―of revealed cores. In particular, the first one will also play a role in the proofs of some results in Section 3, while the second one is a version of the well-known―and widely studied―“satisficing behavior”.

Example 2. Notice that digraph is also a dominance digraph, and for any (hence it is also-trivially-externally stable). Therefore, the identity operator is a revealed core-solution (a-core-solution, ES core-solution).

Example 3. Take and consider the nonempty valued dichotomic choice function as defined by the “lax” satisficing rule for any if, and otherwise. Now, posit i.e. iff and. It is easily checked that for any, (which is also externally stable).

Example 4. By way of contrast, take again and consider the dichotomic choice function as defined by the “strict” satisficing rule for any. It is easily checked that is not a revealed core: to see this, take any. Then, while for any dominance digraph and any, it cannot be the case that hence .

The main objective of this article is precisely to provide a characterization of all revealed cores in, and study their basic order-theoretic structure.

To begin with, let us consider two requirements concerning local existence of nonempty choice sets.

No-dummy property (ND): for any.

2-Properness (2-PR): for any such that.

It is easily checked that ND is satisfied by all revealed cores, while 2-PR is only violated by core solutions when the underlying dominance digraph is not asymmetric. A stronger property that obviously entails both ND and 2-PR is:

Properness (PR): for any nonempty.

The following properties of a choice function play a prominent role, under various labels, in the extant literature:

Chernoff Contraction-consistency (C): for any such that,.

Concordance (CO): for any,.

Superset consistency (SS): for any, if and then.

Property C is a contraction-consistency condition for choice sets in that it requires that any outcome chosen out of a certain set should also be chosen out of any subset of the former: essentially, it says that any good reason to choose a certain option out of a given menu should retain its strength in every submenu of the former containing that option.

Conversely, property CO (also variously denoted as or Generalized Condorcet-consistency) is an expansion-consistency condition for choice sets, requiring that an outcome chosen out of a certain set and of a second one should also be chosen out of the larger set given by the union of those two sets: it says that any good reason to choose a certain option out of two given menus should retain its strength in the larger menu obtained by merging those two menus.

Property SS is also an expansion-consistency requirement for choice sets: it rules out the possibility that the choice set of a certain menu be nonempty and strictly included in the choice sets of a smaller menu.

We are now ready to prove the main results of this paper. Let us start from the following simple.

Claim 5. Let be any (binary) relation on X, and define by the following rule: for any, iff not. Then,

(i);

(ii) for any, , and ;

(iii) R is reflexive iff is irreflexive, and irreflexive iff is reflexive;

(iv) R is total iff is asymmetric, and asymmetric iff is total;

(v) R is quasi-transitive iff is quasi-transitive.

Proof. (i) For any, by definition iff not iff not (not) iff.

(ii) Let, and xRy for all: then, by definition, not for all, and conversely if not for all then not (not xRy) i.e. xRy for all. Similarly, and not yRx for all: then by definition for all, and conversely.

(iii) Indeed, by definition for any, not iff not (not xRx) i.e. xRx. Similarly, not xRx iff.

(iv) Suppose is asymmetric: then, for any, it may be the case that not or not (or both). Now, if not then xRy and if not then yRx, therefore R is total. Conversely, suppose R is total. If xRy then not (not xRy) hence not () and similarly yRx entails not (), thus in any case is asymmetric. Similarly, R is asymmetric iff for any it cannot be the case that xRy and yRx, i.e. by definition iff it is not the case that not and not, namely is total.

(v) Suppose that R is quasi-transitive, and that both and. Then, by definition (not yRx

and xRy), and (not zRy and yRz) i.e. and, hence. Therefore, xRz and not zRx i.e. not and, namely. Conversely, suppose that is quasi-transitive, and that both and. Then, by definition (xRy and not yRx), and (yRz and not zRy) i.e. by definition (not and) and (not and), i.e. and, hence. Therefore, and not i.e. not and, namely. ■

Remark 6. The content of the previous Claim is certainly not unknown, but I have been unable to find a reference in print to it except for the statement of point (iv) in [8] , while Theorem 8 of [3] only includes a specialized version of the same point.

The following Theorem extends and/or supplements some previous characterization results for revealed cores due to [1] and [2] .

Theorem 7. Let. Then, the following statements are equivalent:

(i) c satisfies ND, C and CO;

(ii) there exists an irreflexive such that for any;

(iii) there exists a reflexive relation such that for any.

(iv), is reflexive and for any.

Proof. (i) Þ (iv): Let. Now, for each and, for any, by definition of. Hence. Now, let also satisfy ND, C and CO, and. Then, by definition, and for any there exists such that and. It follows that

and, by CO, whence by C. Therefore, (clearly

it might be the case that). Notice however that, by ND, i.e. for any. Thus, is reflexive, as required. Moreover, if then by C it must also be the case that whence and thus (since by definition).

(ii) Û (iii) (see [1] , Theorem 3): Let. Thus, by Claim 5 (ii), if there exists such that for any, then, for any. Moreover, if R is reflexive then by Claim 5 (iii) is irreflexive hence. Conversely if there exists an irreflexive such that for any then by Claim 5 (ii)-(iii) for any, and is reflexive.

(iii) Þ (iv): See [1] , Theorem 3. Moreover, observe that by definition, and implies i.e. hence (of course, this is an extension to arbitrary choice functions of the proof of the same result for proper choice functions due to [2] ).

(iv) Þ (iii): Trivial.

(iii) Þ (i): Suppose that there exists a reflexive relation such that for any. Clearly, by reflexivity of R, , hence c satisfies ND. Moreover, for any and any, it must also be the case that hence C is also sa- tisfied by c. Finally, for any and, if and then clearly whence and CO is satisfied as well. ■

Remark 8. Notice that the equivalence between statements (ii) and (iii) of Theorem 7 above might in fact be credited to [1] because it is strictly related (indeed, essentially equivalent) to a full-domain specialized version of Theorem 3 of that paper, though the latter concerns nonempty core-solutions over an arbitrary domain hence, strictly speaking, is a statement about a class of proper choice functions on arbitrary domains. On the other hand, [9] has a similar result (see its Theorem 2.5), namely a characterization by the conjunction of C and CO of the choice functions selecting the outcomes “permitted” by all outcomes―or “not prohibited” by any outcome―according to an arbitrary “permission” or “prohibition” binary relation. A characterization of “sums” of revealed cores or “multi-criteria choice functions” by the conjunction of ND and C is suggested in [10] .

Remark 9. The foregoing characterization result is tight. To check that, consider the following examples.

1) Let be defined as follows: for any, if, and where L is a linear order on X and is its bottom element. Clearly, violates ND, but satisfies C and CO;

2) Let, and be defined as follows: for any, , , , and. It is immediately checked that satisfies ND and CO, but violates C since e.g. but;

3) Let be defined as follows: for any, if and otherwise, where L is a linear order on X. It is easily seen that satisfies ND and C, but violates CO.

Next, we have a similar characterization result for revealed a-cores which is also an extension to the general case of possibly non-proper choice functions of previous results as discussed below (see Remark 13).

Theorem 10. Let. Then, the following statements are equivalent:

(i) c satisfies ND, 2-PR, C and CO;

(ii) there exists an irreflexive relation such that for any;

(iii) there exists a total relation such that for any;

(iv), is total and for any.

Proof. (i) Þ (iii): Let satisfy ND, 2-PR, C, and CO. Then, by ND, C and CO (and in view of Theorem 7 above) there exists a reflexive relation R on X such that for each. Thus, by 2-PR, R is total.

(ii) Û (iii): Suppose that there exists a total relation such that for any.

Then, as recorded by Claim 5 (ii) for any. By Claim 5 (iv)

is asymmetric since R is total, hence in particular for any. Conversely, suppose that there exists a dominance digraph such that

, for any. Then, as recorded by Claim 5 (ii)

: by Claim 5 (iv), is total since is asymmetric.

(ii) Þ (i): Suppose that there exists a dominance digraph such that for any. For any, not i.e not by irreflexivity of whence by definition

and ND is therefore satisfied by c. Furthermore, for any, hence. If then,

otherwise or, respectively, hence in any case

thus c satisfies 2-PR.

Also, for any such that, and any, it must be the case that not for all hence in particular not for all, i.e. and c also satisfies C.

Moreover, let and. Then, by definition, not for all and not for all hence not for all i.e. and CO is satisfied by c.

(iii) Û (iv): See the proof of Theorem 7 above. ■

Remark 11. The foregoing characterization result is also tight. To see this, consider the following examples.

1) Let as defined above (see Remark 9). Clearly, violates ND, but satisfies 2-PR, C and CO;

2) Let be defined as follows: for any, and for any such that. It is easily checked that does indeed satisfy ND, C and CO, but clearly violates 2-PR;

3) Let, and as defined above (see Remark 9). It is immediately checked that satisfies ND, 2-PR, and CO, but violates C;

4) Let as defined above (see Remark 9). It is easily seen that satisfies ND, 2-PR and C, but violates CO.

Corollary 12. (see also [2] [4] ) Let. Then, the following statements are equivalent:

(i) c satisfies C and CO;

(ii) there exists a strictly acyclic dominance digraph such that for any;

(iii) there exists a total relation such that for any;

(iv) there exists a relation such that for any.

(v), is total, and for any.

Proof. (i) Þ (ii): Since, c is proper hence in particular it also satisfies ND and 2-PR. Therefore, by Theorem 10 (ii) above, there exists a dominance digraph such that for any. Moreover, since by hypothesis c is proper, for any hence must be acyclic.

In particular, for any, therefore is asymmetric as well. Thus, is

indeed strictly acyclic and for any.

(ii) Þ (i): See the proof of Theorem 7 above.

(i) Û (iii): Obvious, by Theorem 10 above, since, again, entails that c satisfies ND and 2-PR.

(iii) Û (iv): Suppose there exists such that for any. Since, for any. Hence, in particular, for any,. It follows that R is total. The reverse implication is trivial.

(iii) Û (v): See the proof of Theorem 6 above, and of course [2] . ■

Remark 13. Actually, it is well-known that a proper c satisfies both C and CO if and only if there exists a binary relation R on X such that for each and, moreover, as defined above -indeed, for any choice function that satisfies C (see e.g. [2] [4] ). Also notice that the equivalence between (ii) and (iii) is due to [3] . Thus, Corollary 12 is―essentially―a restatement of the Sen-Plott-Suzumura characterization of revealed “rational” (proper) choice functions or, equivalently, revealed non-empty core solutions.

Let us now turn to characterizations of revealed externally stable core-solutions. Since externally stable cores (of nonempty sets) are nonempty the corresponding choice functions are proper: thus, given the traditional focus on proper choice functions, this subclass of revealed cores is the most widely studied, and best known (thanks again to [1] and [4] ; it should also be recalled here that externally stable cores are in particular a subclass of unique Von Neumann-Morgenstern stable sets). Therefore, for the sake of convenience, we collect in the following Theorem a few notable characterizations of revealed externally stable cores (to the best of the author’s knowledge, only some of them are already known and available in print, namely those recorded in [4] which correspond to the first equivalence of the following Theorem, as mentioned explicitly in its proof below).

Theorem 14. Let. Then, the following statements are equivalent:

(i) c satisfies PR, C, CO and SS;

(ii) there exists a quasi-transitive relation such that for any nonempty;

(iii) there exists a total and quasi-transitive relation such that for any nonempty;

(iv), is total and quasi-transitive, and for any.

(v) there exists a reflexive and negatively transitive relation such that for any nonempty;

(vi) there exists a negatively transitive relation such that for any nonempty;

(vii) there exists an irreflexive relation such that with externally stable, for any;

(viii) there exists an irreflexive and transitive relation such that for any nonempty;

(ix) there exists a a strict partial order such that for any nonempty.

Proof. (i) Þ (ii) ( [10] ): By Theorem 2.6 of [4] , if c satisfies PR, C, CO and SS then there exists a (reflexive and) quasi-transitive relation such that for any nonempty. But of course PR entails that for any, hence R is total as well.

(ii) Þ (i) ( [10] ): See again [4] , Theorems 2.5, 2.6 and 2.7.

(ii) Û (iii): Let be quasi-transitive and such that for any nonempty. Of course, PR entails that in particular for any, hence R is total as well. The reverse implication is trivial.

(iii) Û (iv): See the proof of Theorem 7 above.

(iii) Û (v): Let be total and quasi-transitive, and such that not xRy and not yRz. Hence, yRx and zRy since R is total. Therefore, by definition, yR^ax and zR^ay. By quasi-transitivity, it follows that zR^ax, whence in particular not xRz i.e. R is negatively transitive. Moreover, totality implies reflexivity of R. Conversely, let be reflexive and negatively transitive. Suppose there exist such that not xRy and not yRx: then, by negative transitivity, not xRx, a contradiction since R is reflexive. Thus, R is also total. Moreover, let xR^ay and yR^az. Then, in particular, not yRx and not zRy. It follows that, by negative transitivity, not zRx whence, by totality, xRz. Thus, xR^az i.e. R is quasi-transitive as well.

(v) Û (vi): Let be a negatively transitive relation such that for any nonempty. Then in particular, for any, hence R is reflexive as well. The reverse implication is trivial.

(iii)Þ (vii): Let be total, quasi-transitive and such that for any nonempty. Clearly, by construction, i.e.

for any (see Claim 5 (i) above). Moreover, by Claim 5 (iii), is asymmetric since R is total, hence. Now, take any. By definition, there exists such that. If we are done. Suppose then that as well: thus, there exists such that. It follows, by finiteness of Y and nonemptiness of, that there exists a finite k such that for any, and. Since is asymmetric, it also follows that, hence is externally stable.

(vii) Þ (i): Suppose that there exists a dominance digraph such that with externally stable, for any. By definition of external stability, for any nonempty, hence c satisfies PR. Moreover, by Theorem 7 (ii) above (or, for that matter, by Theorem 8 (ii)), it also satisfies C and CO. Finally, consider such that, and suppose there exists i.e.. Then, by external stability of, there exists such that, a contradiction since. Therefore, c satisfies SS as well.

(viii) Û (iii): Suppose that there exists a dominance digraph such that is transitive (hence in particular quasi-transitive) and for any nonempty. Then, by Claim 5 (i)-(ii) above, for any nonempty. Moreover, by Claim 5 (v), is quasi-transitive. Also, notice that since by hypothesis is both irreflexive and transitive, it must be asymmetric as well. Therefore, by Claim 5 (iv), is total. Conversely, suppose that there exists a total and quasi-transitive relation such that for any nonempty. Then, by Claim 5 (ii) for any nonempty. Moreover, by Claim 5 (iii), (v), and in view of quasi-transitivity and totality of R, is both quasi-transitive and asymmetric, hence transitive as well, and such that as required.

(viii) Û (ix): Suppose that there exists a dominance digraph such that is transitive and for any nonempty. Again, irreflexivity and transitivity imply asymmetry of, which is therefore a strict partial order. The reverse implication is trivial. ■

Remark 15. Observe that the characterization result of revealed externally stable cores in terms of properties of choice functions included in Theorem 14 is also tight. To see this, consider the following examples.

1) Let as defined above (see Remark 9). Clearly, violates PR,but satisfies C, CO and SS;

2) Let, and as defined above (see Remark 9). It is immediately checked that satisfies PR,CO and SS, but violates C;

3) Let, and such that for any, ,

, and. Clearly, satisfies PR, C and SS. However, fails to satisfy CO since;

4) Let, and such that for any, ,

, and. Clearly, satisfies PR, C and CO but fails

to satisfy SS since.

Remark 16. Notice again that Theorem 14 above is essentially a refinement of well-known results due to Suzumura (see e.g. [4] , Theorems 2.8 and 2.10) and [3] , whose Theorems 3, 4, and 7 amount essentially to the equivalence between statements (iii), (iv) and (vii). It should also be mentioned here that the conjunction of C and SS turns out to be equivalent (see e.g. [4] ) to another well-known and widely used property, namely:

Path Independence (PI): for any,.

Thus, the equivalent statements of Theorem 14 are also equivalent to the statement “satisfies PR, PI and CO”.

It should be remarked that the characterizations provided above are in general quite straightforward extensions to arbitrary choice functions (with full domain) of previously known results concerning proper choice functions (with full domain). Indeed, the gist of the results offered in the present section may be summarized as follows:

(i) remarkably, the characterizations of general revealed cores and a-cores considered here consist of the very same properties used to characterize their nonempty-valued counterparts as supplemented with very mild-look- ing local nonemptiness requirements for choice sets of singleton and two-valued subsets, respectively;

(ii) the exact correspondence between revealed core-solutions and maximizing “rational” choice functions is confirmed to hold within the general space of arbitrary choice functions: the alleged extra-generality of the latter subclass that has sometimes been alluded to in the literature (as e.g. in [4] , p. 21) does not materialize within the space of (total) choice functions and is therefore strictly confined to the realm of partial choice functions;

(iii) finally, and most notably, the class of general revealed cores turns out to inherit some of the supplementary order-theoretic structure enjoyed by its larger ambient space as compared to the smaller and less regular space of proper choice functions: that is precisely the topic of the next section.

3. Posets and Semilattices of Revealed Cores

Let us now turn to a global description of the order-theoretic structure of the class of all revealed core-solutions (a-core-solutions, nonempty-valued core-solutions, externally stable core-solutions, respectively).

A partially ordered set or poset is a pair where P is a set and is a reflexive, transitive and antisymmetric binary relation on P (i.e. for any, and for any, whenever and, and whenever and). For any we posit. A coatom of a poset with a top element or maximum is any which is covered by -written -i.e. and for any such that. The set of all coatoms of P is denoted. Dually, an atom of P is any which is an upper cover of -written -i.e. and for any such that. The set of all atoms of P is denoted.

A poset is a meet semilattice (join semilattice, respectively) if for any the -greatest lower bound (the -least upper bound, respectively) of does exist. Moreover, P is a lattice if it is both a meet semilattice and a join semilattice.

A lattice is bounded if there exist both a bottom element and a top element (hence in particular a finite lattice is also bounded), distributive iff for any, complemented if it is bounded and for any there exists such that and, and Boolean iff it is both distributive and complemented.

A meet semilattice is lower distributive if is a distributive lattice for any, and

has the coronation (or join-Kelly) property if―for any - exists in P whenever and also exist. A meet semilattice is median if it is lower distributive and has the coronation property.

The set of all choice functions on X can be endowed in a natural way with the point-wise set inclusion partial order by positing, for any, iff for each. Clearly, the identity operator is its top element, and the constant empty-valued choice function its bottom element. It is well-known, and easily checked, that is in fact a Boolean lattice with join (i.e. set-union) and meet (i.e. set-intersection), both defined in the obvious component-wise manner: see e.g. [11] .

For any such that, and are defined as follows: for all, if, and otherwise, and for all,

, and for all such that and. Moreover,

, and.

The minimum ND choice function is defined by the following rule: for any, , and for any such that.

Now, let denote the set of all revealed core-solutions on X, the set of all revealed asymmetric core-solutions, the set of all revealed nonempty-valued core-solutions, and the set of all revealed externally stable core-solutions on X, respectively). We also denote with a slight abuse of

notation, , and the corresponding subposets of (where

denotes, , and, respectively). We have the following.

Theorem 17. The poset of revealed core-solutions is a sub-meet-semilattice of with itself as its top element, but not a sub-join-semilattice of. It also satisfies the coronation property hence it is a median meet semilattice. The bottom element of is the minimum ND choice function. Moreover, the set of coatoms of is, and the set of its atoms is.

Proof. Let, and consider. Clearly, for any, since c and satisfy ND: hence does also satisfy ND.

Moreover, for any, since c and both satisfy C,

hence satisfies C.

Finally, since c and satisfy CO, for any,

and CO also holds for. It follows that, by Theorem 7 above, , whence is a sub-meet-semilattice of: in particular, it follows that is lower distributive.

Furthermore, let us suppose that. Then, take as defined in the obvious way. It is immediately checked that does satisfy ND and C, by construction.

Thus, we only have to check that does also satisfy CO. In order to check this last point, consider any, and.

By definition, it follows that for some. Hence, in particular, it also follows that for some. Now, by hypothesis, hence it satisfies CO. Therefore, and also satisfies CO. As a consequence,: thus, has the join-Kelly property and is therefore a median meet-semilattice as claimed.

It is easily checked that, the top element of, does also satisfy ND, C and CO hence as observed above (see Example 2).

Now, consider as defined above: it satisfies ND, by definition, and, being nonempty-valued precisely on singletons, it trivially satisfies C and CO as well. Thus,. On the other hand, for any, c must satisfy ND, hence.

Next, take any. Notice that, by definition, satisfies ND. Also, if then the follow- ing cases may be distinguished: a); b) and; c). If then; if and then

; if then: thus in any case C holds. Furthermore, let: then by definition and. Assume now that. Then, and while. It follows that, a contradiction. Thus, CO is also satisfied by, Theorem 7 applies, and.

Moreover, by definition i.e. and.

Let be such that, and assume that i.e. there exists such that. Clearly, by Theorem 7, c satisfies ND, C and CO. If there is nothing to prove, so assume that there also exists such that. Notice that by definition of, entails and, hence in particular. Also, there exists. By definition of again, entails, and (whence). Therefore, whence, by C,.

Suppose first that, and consider. Clearly, by definition, . Thus, hence, by CO,: a contradiction, since. Suppose then: since by hypothesis, there exists an irreflexive digraph such that for any. Therefore, entails that in turn entails since: a contradiction again because.

It follows that if then either or i.e. is indeed a coatom of.

Conversely, let c be a coatom of and suppose. Then, for any pair of distinct, neither nor i.e. there exist such that and. Thus, by definition, and, while there exists such that. Hence, consider any: then, there exists such that and. By C, i.e. for any while, which contradicts CO in view of finiteness of X.

To check that each is an atom of, notice first that. Indeed, satisfies ND by construction. Also, if then entails that either for some, or i.e. either A is a singleton or. Thus, in any case, if then by definition hence satisfies C. Moreover, for any, if then by definition of either or (and): thus, in any case,

and CO is also satisfied by. Next, observe that for any, and

while. Thus, for any (indeed, for any) if

then either or.

Conversely, assume that c is an atom of and. Then, by definition of, for any A such that, and there exists such that and. It follows that, for any and any, , therefore violating C, a contradiction by Theorem 7.

To check that is not a sub-join-semilattice of, just consider without loss of generality, and .

Now, posit and for any. By definition, , , and hence, while

, which contradicts CO. ■

Remark 18. Notice that finiteness of X has been used in the proof above in order to show that the set of coatoms of is contained in. The latter statement clearly holds for an infinite X as well provided CO is replaced with the following stronger version of “Concordance” .

CO*: for any family of subsets of X,.

Remark 19. Since is a semilattice with a top element (and indeed a finite one, under finiteness of X), it follows that it is also a lattice with meet = and join of a pair given by the meet of the (nonempty) set of upper bounds of that pair (see e.g. [12] ), which is however not a sublattice of.

Thus, the poset of revealed core-solutions enjoys the remarkably regular structure of a median meet-semilat- tice. Notice that an important consequence of that fact is the following: any profile of revealed cores admits medians and the latter coincide with the simple majority consensus revealed core if the profile consists of an odd list of revealed cores. Therefore, in case several revealed cores are to be considered for aggregation, due perhaps to locally missing or unreliable data and/or plurality of information sources, an amalgamation process by means of the simple majority aggregation rule is available (see e.g. [11] for some results on posets and lattices of other classes of choice functions and related aggregation rules in the same vein).

The posets of revealed a-core-solutions, nonempty-valued core-solutions, and externally stable core-solutions are considerably less regular, as recorded by the following results, namely:

Theorem 20. The poset of revealed a-core-solutions has a top element, , and is the set of its coatoms, but it is neither a sub-meet-semilattice nor a sub-join-semilattice of. The minimal elements of are the choice functions that satisfy ND, 2-PR, C, CO and such that (a) for any and (b) not for any that satisfies ND, 2-PR, C and CO.

Proof. To check that is indeed the top element of it is only to be observed―in view of Theorem 7―that does in fact also satisfy 2-PR. Similarly―in view of Theorem 7 and of the proof of Theorem 17 provided above―to see that is the set of coatoms of it is only to be checked that any does also satisfy 2-PR (which is clearly the case, by definition).

The proof of Theorem 17 already establishes that is not a sub-join-semilattice of since, as it is easily checked, and as defined there do belong to.

Next, consider and defined as follows: assume without loss of generality, and take, (notice that both and are asym- metric digraphs); then, for any, posit and. Clearly, by definition,.

However,.

Therefore, violates 2-PR hence by Theorem 7. It follows that is not a sub-meet-semilattice of.

The last statement about minimal elements of is a straightforward consequence of Theorem 10. ■

Theorem 21. The poset of nonempty-valued core-solutions has a top element, , and is the set of its coatoms, but it is neither a sub-meet-semilattice nor a sub-join-semilattice of. The minimal elements of are the single-valued choice functions that satisfy C and CO.

Proof. First, notice that by definition is proper, hence since as previously shown it is a core-solution. Also, it is immediately checked that, by definition, any is proper. Therefore, the proof of Theorem 17 also establishes that is the set of coatoms of. In the same vein, it is immediately checked that -as defined above in the proofs of the two previous Theorems-are also proper. It follows, by those proofs, that is neither a sub-meet-semilattice nor a sub-join-semilattice of. The final statement about minimal elements of is an immediate consequence of Corollary 12. ■

Theorem 22. The poset of revealed externally stable core-solutions, has a top element, , and is the set of its coatoms, but it is neither a sub-meet-semilattice nor a sub-join-semilattice of. The minimal elements of are the single-valued choice functions that satisfy C, CO and SS.

Proof. Observe that for any, if then of course i.e. whence and SS is clearly satisfied by. In view of Theorem 14, this establishes that is also the top element of. Also, it is immediately checked that any satisfies SS: indeed, let be such that and. Since, the following jointly exhaustive cases are to be distinguished: a); b); c) and. Under a), and hence. Under b), and hence again. Under c), and whence i.e.. By hypothesis, hence: thus, and and therefore . It follows that does in fact satisfy SS. Therefore, the proof of Theorem 17 also establishes that is the set of coatoms of.

Finally, it is immediately checked by direct inspection that―as defined above in the proofs of Theorems 17 and 20―do also (trivially) satisfy SS. It follows, by the very same proofs, that is neither a sub-meet-semilattice nor a sub-join-semilattice of. The final statement about minimal ele- ments of is an immediate consequence of Theorem 14. ■

Thus, while only the poset of revealed core-solutions is a (meet) sub-semilattice of all the posets of revealed cores defined above share their top element and set of coatoms.

4. Concluding Remarks

Choice functions with full domain which may be regarded as core-solutions or externally stable core solutions of an underlying dominance digraph have been characterized both in the general case and for asymmetric dominance digraphs. Both characterizations combine a version of the usual mix of contraction consistency and expansion consistency conditions which are required for the special case of proper i.e. nonempty-valued choice functions with a suitable local nonemptiness requirement for choice sets. The characterizations provided above have also been shown to be helpful for a simple analysis of the basic order-theoretic structure of revealed cores. In particular, as mentioned in the Introduction, every revealed core embodies a considerable part of the structure of standard maximizing choice functions, while the global structure of (full domain) revealed cores retains precisely the median semi-latticial properties of the space of all (full domain) choice functions that are most significant from the point of view of simple majority aggregation. The latter property, however, is not shared by asymmetric or externally stable revealed cores.

An obvious extension of the present paper should address the characterization problem for revealed cores on arbitrary domains. That open issue is left as a topic for further research.

Conflicts of Interest

The authors declare no conflicts of interest.

References

[1]	Wilson, R.B. (1970) The Finer Structure of Revealed Preference. Journal of Economic Theory, 2, 348-353. http://dx.doi.org/10.1016/0022-0531(70)90018-9
[2]	Sen, A.K. (1971) Choice Functions and Revealed Preference. Review of Economic Studies, 38, 307-317. http://dx.doi.org/10.2307/2296384
[3]	Plott, C. (1974) On Game Solutions and Revealed Preference Theory. Social Science Working Paper 35, California Institute of Technology, Division of the Humanities and Social Sciences, Pasadena.
[4]	Suzumura, K. (1983) Rational Choice, Collective Decisions, and Social Welfare. Cambridge University Press, Cambridge.
[5]	Aizerman, M. and Aleskerov, F. (1995) Theory of Choice. Amsterdam, North Holland.
[6]	Danilov, V. and Koshevoy, G. (2009) Choice Functions and Extensive Operators. Order, 26, 69-94. http://dx.doi.org/10.1007/s11083-009-9108-x
[7]	Bossert, W. and Suzumura, K. (2010) Consistency, Choice, and Rationality. Harvard University Press, Cambridge.
[8]	Vannucci, S. (2009) Choosing VNM-Stable Sets of the Revealed Dominance Digraph. DEP Working Paper 576, Siena.
[9]	Monjardet, B. (2007) Some Order Dualities in Logic, Games and Choices. International Game Theory Review, 9, 1-12. http://dx.doi.org/10.1142/S0219198907001242
[10]	Danilov, V., Koshevoy, G. and Savaglio, E. (2015) Hyper-Relations, Choice Functions, and Orderings of Opportunity Sets. Social Choice and Welfare, 45, 51-69. http://dx.doi.org/10.1007/s00355-014-0844-5
[11]	Davey, B.A. and Priestley, H.A. (1990) Introduction to Lattices and Order. Cambridge University Press, Cambridge.
[12]	Monjardet, B. and Raderanirina, V. (2004) Lattices of Choice Functions and Consensus Problems. Social Choice and Welfare, 23, 349-382. http://dx.doi.org/10.1007/s00355-003-0251-9