A Production Inventory Model of Power Demand and Constant Production Rate Where the Products Have Finite Shelf-Life

Shirajul Islam Ukil¹, Mohammad Ekramol Islam², Md. Sharif Uddin¹

¹Department of Mathematics, Jahangirnagar University, Savar, Dhaka, Bangladesh.
²Department of Business Administration, Northern University Bangladesh, Dhaka, Bangladesh.

DOI: 10.4236/jssm.2015.86088                

Abstract

A production inventory model has been developed in this paper, basing on constant production rate and market demand, which varies time to time. Seeing the demand pattern the proposed model has been formulated in a power pattern which can be expressed in a linear or exponential form. The model finds the total average optimum inventory cost and optimum time cycle. The model also considers the small amount of decay. Without having backlogs, production starts. Reaching at the desired level of inventories, it stops production. After that due to demands along with the deterioration, it initiates its depletion and after certain periods the inventory gets zero. The model has also been justified with proving the convex property and by giving a numerical example with the sensitivity test.

Keywords

Production Inventory, Shelf-Life, Power Demand, Linear Demand, Exponential Demand and Production Rate

Received 25 November 2015; accepted 26 December 2015; published 29 December 2015

1. Introduction

In last few decades, inventory problems have been studied in a large scale. Inventory is related to stock the items before delivering to the customers. If we visualize our daily needs, we can see that these needs are of two kinds as far as deterioration or decay is concerned. Items like radioactive substances, food grains, fashionable items, pharmaceuticals etc. are one kind, which have finite shelf-life, i.e. limited life once in the shelf, or have a sufficient deterioration after a particular time. On the other hand, the items like bricks, steels, heavy woods etc. are the other kind which does not have that much of deterioration the one mentioned before. Due to the limited shelf-life and market demand, the stock level or inventory continuously decreases and in this way deterioration occurs. This deterioration affects the inventory seriously and inventory cost increases. To make the inventory cost at optimum level i.e. to get the minimum inventory cost, a suitable inventory model is required which suits to meet the actual demand in the market. In minimizing inventory cost this paper proposes an inventory model with power demand, small amount of decay and constant production rate, whereas the existing models very often ignore the production rate; instead those consider the instantaneous replenishment rate. The power demand defines that kind of demand which varies with change of power in the power function.

The organizations give due importance to few parameters which affect the model. Like, in this proposed model power demand has been considered as the market may have a demand of linear type, again shortly it may have the demand of exponential function. The linear demand means that the firms receive demand either in an increasing or decreasing way, but gradually, not suddenly, i.e. demand as a linear function. Again, the exponential demand means the demand either in an exponentially increasing way or exponentially decreasing way suddenly. It may be clarified more giving an example, like, is an exponential demand. If the value of x increases, the value of 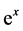increases geometrically. Again 2x can be treated as linear demand as the value of x increases, the value of 2x increases slowly. To develop a new model, we have considered that the production rate is constant and greater than demand rate at any time. Production starts when inventory level is zero. Inventory level is highest at 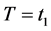and after this point, the inventory depletes quickly due to demand only. Demand is considered a type of power pattern in this paper i.e. the form of linear or exponential. For unit inventory, amount of decay rate is very small and constant.

Satisfying the convex property and using a numerical example, the paper could justify that the objective of formulating this model is achieved. The objective of the proposed model is to get the optimum inventory cost and optimum time cycle by introducing a time dependent inventory model with constant production rate and power demand. The paper subsequently advances with literature review, assumptions, notations used in the model, development of the model, numerical illustration, sensitivity analysis, conclusion and suggestions for future work in this field.

2. Literature Review

Many researchers have work in the field of inventory problems or in production inventory model to solve the real life problems by building the suitable inventory models. On ground, the business institution faces various types of demand. Demand may be linear, quadratic, exponential, time dependent, level or stock dependent, price dependent etc. Basing on the demand pattern, the firms decide how much to produce and when to produce. Initially, Harris [1] discusses inventory model in 1915. Whitin [2] was the first researcher to develop the inventory model for fashionable goods considering its little decay in the inventory. Ghare and Schrader [3] first pointed out the effect of decay in inventory analysis and discovered the economic order quantity (EOQ) model. They showed the nature of the consumption of the deteriorating items. Sarker et al. [4] explained an inventory model where demand was a composite function consisting of a constant component and a variable component proportional to inventory level in a period in which decay was exponential and inventory was positive. Teng et al. [5] developed the model with deteriorating items and shortages assuming that the demand function was positive and fluctuating with respect to time. Skouri and Papachristos [6] discussed a continuous review inventory model considering the five costs as deterioration, holding, shortage, opportunity cost due to the lost sales and the replenishment cost due to the linearly dependency on the lot size. Chund and Wee [7] developed an integrated two stages production inventory deteriorating model for the buyer and the supplier on the basis of stock dependent selling rate considering imperfect items and just in time (JIT) multiple deliveries. Applying inventory replenishment policy Mingbao and Wang [8] expressed the inventory model for deteriorating items with trapezoidal type demand rate, where the demand rate is a piecewise linearly functions. Hassan and Bozorgi [9] developed the location of distribution centers with inventory. Chang and Dye [10] expressed an inventory model with deteriorating items, with time varying demand and partial backlogging. Tripathy and Mishra [11] discuss the inventory model with ordering policy for weibull deteriorating items, quadratic demand, and permissible delay in payments. Sarkar et al. [12] introduced and inventory model with finite replenishment rate, trade credit policy and price discount offer. Khieng et al. [13] presented a production model for the lot-size, order level inventory system with finite production rate and the effect of decay. Ekramol [14] [15] considered various production rates assuming the demand is constant. Mishra et al. [16] explained an inventory model for deteriorating items with time dependent demand and time varying holding cost under partial backlogging. Aggarwal [17] developed an order level inventory model for a system constant rate of deterioration. Shiraj [18] discussed the effect of just in time manufacturing system on EOQ model. Sivazlian and Stenfel [19] determined the optimum value of time cycle by using the graphical solution of the equation to obtain the economic order quantity model. Shah and Jaiswal [20] and Dye [21] established an inventory model by considering demand as a function of selling price and three parameters of Weibull rate of deterioration. Billington [22] discussed classic economic production quantity (EPQ) model without backorders or backlogs. Pakkala and Achary [23] established a deterministic inventory model for deteriorating items with two warehouses, while the replenishment rate was finite, demand was uniform and shortage was allowed. Abad [24] discussed regarding optimal pricing and lot sizing under conditions of perish ability and partial backordering. Sing and Pattanak [25] -[27] developed the model for deterioration and time dependent quadratic demand under permissible delay in payment, whereas, we have used the exponential demand with constant production, but ignoring the payment aspect. Amutha and Chandrasekaran [28] formulated the inventory model with deterioration items, quadratic demand and time dependent holding cost. But in our proposed model, we have emphasized on the production rate, power demand and constant holding cost. Ouyang and Cheng [29] explained the inventory model for deteriorating items with exponential declining demand and partial backlogging [30] . Dave and Patel introduced an inventory model for deteriorating Items with time proportional demand, whereas in our proposed model we have included demand in a power pattern.

3. Development of the Model

To develop the proposed model it needs numbers of notations or symbols to clarify the assumptions considered and description explained in this paper. The notations or symbols used in this paper are cited in Table 1 below.

There may be various types of demand of different types of items in the market. At times it may be linear. Again within vary short span of time it may be changed into exponential type of demand. Taking this type of situation into cognizance, this model is developed. The model is suitable for those kinds of products which have finite shelf-life and ultimately causes the products decay. At the beginning, while time, the production starts with zero inventory with the rate 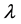which remains constant for entire production cycle. We have considered the demand as a power function which will be in various forms due to the different values of n. Say for example, if we consider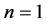, the demand function 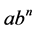will be linear and for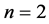, it will be exponential. We build up the model by considering the demand as power function in general. Here, demand function in Figure 1 indicates the linear function as a kind of power function:

Table 1. Notations.

Figure 1. Inventory model with linear demand.

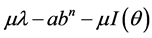During the period, to, the inventory increases at the rate of, as 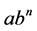is the demand in the market and 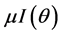is the decay of inventories at instant where, is the decay of unit inventory in the period. By using the above arguments we can have the following equation:

The general solution of the differential equation is,

We now apply the following boundary condition, at, we get,

By solving we get,.

Therefore, (1)

Putting another boundary condition, i.e. at, , taking up to first degree of,we get the following equation:

Thereby, (2)

With the help of Equation (1) and by considering up to second degree of, the total un-decayed inventory during to we get,

(3)

Considering the decay of the items, we calculate the deteriorating items during the period as below:

(4)

Again during to, the inventory decreases at the rate of, as there is no production after time and inventory reduces due to market demand only. Applying the similar arguments as used before, we get the differential equation as mentioned below:

The general solution of the differential equation is defined below:

Applying the boundary condition at, we get,.

By solving we get,

Therefore, (5)

Putting another boundary condition, i.e. at, , taking up to first degree of,we get the following equation:

Thereby, (6)

Now, with the help of Equation (5) and by considering up to the second degree of we get the un-decayed inventory during to as:

(7)

Considering the decay of the items, we calculate the deteriorating items during the period as below:

(8)

From Equations (2) and (6) we get,

Therefore, (9)

Total Cost Function: The cost function can be written in the form given below:

(10)

By using Equations (3), (4), (7) and (8) in (10), we get the following result,

Now using Equations (2) and (9) we get the value as,

(11)

The objective is now to find out the order quantity that minimizes the total inventory cost for the inventory system. The cost depicts Equation (11). In order to determine the optimum order quantity and to verify that Equation (11) is convex in, we must show that the following two well known properties hold,

1) and;

2).

From the convex property 1) i.e. we get the equation as below:

or,

Therefore, the optimum order quantity,

(12)

Now again differentiating the Equation (11) with respect to, we get,

(13)

From Equation (13) we can conclude that the convex property 2) i.e., as and all are positive.

Finally, we can conclude that the equation of total cost function (11) is convex in. Hence, there is an optimal solution in for which the total cost function will be minimal.

4. Numerical Illustration

1) Situation 1: When n = 1 (Demand is Linear Function)

In order to give an example with numerical illustration, let us suppose the following parameters, while:

and.

After putting all the values in Equations (2), (9), (11) and (12) we get the following results:

・ Optimum time units at maximum inventory level.

・ Optimum order interval units.

・ Total average optimum inventory cost units and.

・ Optimum order quantity units respectively.

Putting the values of arbitrarily either bigger or lesser than, we get the inventory cost gradually increased from the total average optimum inventory cost, which is shown in Table 2 and Figure 2 respectively:

It can be mentioned that in the demand function shows the demand function is a linear form which is depicted in Figure 1 before.

2) Situation 2: When n = 2 (Demand is Exponential Function)

In order to give an example with numerical illustration, let us suppose same parameter we have considered in the first situation as below while:

and.

After putting all the values in equation no (2), (9), (11) and (12) we get the following results:

・ Optimum time units at maximum inventory level.

・ Optimum order interval units.

・ Total average optimum inventory cost units and.

・ Optimum order quantity units respectively.

Putting the values of arbitrarily either bigger or lesser than, we get the inventory cost gradually increased from the total average optimum inventory cost, which is shown in Table 3 and Figure 3 respectively:

In this case, it is observed that in the demand function shows the demand function is an exponential form which is depicted in Figure 4.

5. Sensitivity Analysis

Now assuming the set up cost fixed, we study the effects of changes of parameters and on the optimal length of ordering cycle, optimal time cycle, optimal order quantity, and the total average inventory cost per unit time in the model. We performed the sensitivity analysis by changing each of the parameters by +50%, +25%, +10%, −10%, −25% and −50% taking one parameter at a time while keeping other parameters unchanged. The details are shown in Table 4.

Table 2. Order quantity verses inventory cost for n = 1 (when demand is linear).

Table 3. Order quantity verses inventory cost for n = 2 (when demand is exponential).

Figure 2. Quantity verses total cost.

Figure 3. Quantity verses total cost.

Figure 4. Inventory model with exponential demand.

Table 4. Sensitivity analysis for n = 1 (when demand is linear).

Analyzing the results in the above table we can summarize the following observations:

1) and decreases while increases in the value of the parameter. Here is highly sensitive to and moderately sensitive to all other values in the model.

2) and increases and decreases while primarily decreases and then again increases with increase in the value of the parameter and. Here, and are highly sensitive to, and and those are moderately sensitive to. In the other hand, is highly sensitive to as well as and it is moderately sensitive to and.

3) decreases and increases while and remain unchanged with increase in the value of the parameter. Here is highly sensitive to and moderately sensitive to.

4) and increases while and remain unchanged with increase in the value of the parameter. is moderately sensitive to and.

Analyzing the results in Table 5 we can summarize the following observations:

Table 5. Sensitivity analysis for n = 2 (when demand is exponential).

1) and decreases while increases with increase in the value of the parameter. Here is highly sensitive to as well as and highly sensitive to and.

2) and increases while decreases with increase in the value of the parameter. Here is highly sensitive to as well as and moderately sensitive to and.

3) and increases while and decreases with increase in the value of the parameter and. Here and are highly sensitive to as well as and moderately sensitive to and.

4) decreases and increases while and remain unchanged with increase in the value of the parameter and.

6. Conclusion

In the present context of modern age, without the inventory management, the business institution cannot think ahead. By the proper management and thereby developing the suitable inventory model, the institution only can save its production inventory cost. Market demand is always fluctuate. The model is developed considering this demand. Maybe, today the market demand is very high and tomorrow it is low. The inventory model we have proposed in this paper can be suitable to meet both the demands linear or exponential. Because of deterioration, this model also gives the correct result in which the materials have the finite shelf-life. In the proposed model, the production rate and the decay have been considered constant all through. The model develops an algorithm to determine the optimum ordering cost, total average inventory cost and optimum time cycle. The model could establish that with a particular order level the inventory cost is minimal. Here, for n = 1, we got units and total average inventory cost units and for n = 2, we got units and total average inventory cost units, before and after this point total cost increases sharply.

Conflicts of Interest

The authors declare no conflicts of interest.

References

[1]	Harris, F.W. (1915) Operations and Costs. A. W. Shaw Company, Chicago, 48-54.
[2]	Whitin, T.M. (1957) Theory of Inventory Management. Princeton University Press, Princeton, 62-72.
[3]	Ghare, P.M. and Schrader, G.F. (1963) A Model for an Exponential Decaying Inventory. Journal of Industrial Engineering, 14, 238-243.
[4]	Sarker, B.R., Mukhaerjee, S. and Balam, C.V. (1997) An Order Level Lot Size Inventory Model with Inventory Level Dependent Demand and Deterioration. International Journal of Production Economics, 48, 227-236. http://dx.doi.org/10.1016/S0925-5273(96)00107-7
[5]	Teng, J.T., Chern, M.S. and Yang, H.L. (1999) Deterministic Lot Size Inventory Models with Shortages and Deteriorating for Fluctuating Demand. Operation Research Letters, 24, 65-72. http://dx.doi.org/10.1016/S0167-6377(98)00042-X
[6]	Skouri, K. and Papachristos, S. (2002) A Continuous Review Inventory Model, with Deteriorating Items, Time Varying Demand, Linear Replenishment Cost, Partially Time Varying Backlogging. Applied Mathematical Modeling, 26, 603-617. http://dx.doi.org/10.1016/S0307-904X(01)00071-3
[7]	Chund, C.J. and Wee, H.M. (2008) Scheduling and Replenishment Plan for an Integrated Deteriorating Inventory Model with Stock Dependent Selling Rate. International Journal of Advanced Manufacturing Technology, 35, 665-679. http://dx.doi.org/10.1007/s00170-006-0744-7
[8]	Cheng, M. and Wang, G. (2009) A Note on the Inventory Model for Deteriorating Items with Trapezoidal Type Demand Rate. Computers and Industrial Engineering, 56, 1296-1300. http://dx.doi.org/10.1016/j.cie.2008.07.020
[9]	Shavandi, H. and Sozorgi, B. (2012) Developing a Location Inventory Model under Fuzzy Environment. International Journal of Advanced Manufacturing Technology, 63, 191-200. http://dx.doi.org/10.1007/s00170-012-3897-6
[10]	Chang, H.J. and Dye, C.Y. (1999) An EOQ Model for Deteriorating Items with Time Varying Demand and Partial Backlogging. Journal of the Operation Research Society, 50, 1176-1182. http://dx.doi.org/10.1057/palgrave.jors.2600801
[11]	Tripathy, C.K. and Mishra, U. (2010) Ordering Policy for Weibull Deteriorating Items for Quadratic Demand with Permissible Delay in Payments. Applied Mathematical Science, 4, 2181-2191.
[12]	Sarkar, B., Sana, S.S. and Chaudhuri, K. (2013) An Inventory Model with Finite Replenishment Rate, Trade Credit Policy and Price Discount Offer. Journal of Industrial Engineering, 2013, 1-18.
[13]	Khieng, J.H., Labban, J. and Richard, J.L. (1991) An Order Level Lot Size Inventory Model for Deteriorating Items with Finite Replenishment Rate. Computers Industrial Engineering, 20, 187-197. http://dx.doi.org/10.1016/0360-8352(91)90024-Z
[14]	Ekramol, M.I. (2004) A Production Inventory Model for Deteriorating Items with Various Production Rates and Constant Demand. Proceedings of the Annual Conference of KMA and National Seminar on Fuzzy Mathematics and Applications, Payyanur, 8-10 January 2004, 14-23.
[15]	Ekramol, M.I. (2007) A Production Inventory with Three Production Rates and Constant Demands. Bangladesh Islamic University Journal, 1, 14-20.
[16]	Mishra, V.K., Singh, L.S. and Kumar, R. (2013) An Inventory Model for Deteriorating Items with Time Dependent Demand and Time Varying Holding Cost under Partial Backlogging. Journal of Industrial Engineering International, 9, 1-4. http://dx.doi.org/10.1186/2251-712x-9-4
[17]	Aggarwal, S.P. (1978) A Note on an Order Level Inventory Model for a System Constant Rate of Deterioration. Opsearch, 15, 184-187.
[18]	Ukil, S.I., Ahmed, M.M., Sultana, S. and Uddin, M.S. (2015) Effect on Probabilistic Continuous EOQ Review Model after Applying Third Party Logistics. Journal of Mechanics of Continua and Mathematical Science, 9, 1385-1396.
[19]	Sivazlin, B.D. and Stenfel, L.E. (1975) Analysis of System in Operations Research. 203-230.
[20]	Shah, Y.K. and Jaiswal, M.C. (1977) Order Level Inventory Model for a System of Constant Rate of Deterioration. Opsearch, 14, 174-184.
[21]	Dye, C.Y. (2007) Joint Pricing and Ordering Policy for a Deteriorating Inventory with Partial Backlogging. Omega, 35, 184-189. http://dx.doi.org/10.1016/j.omega.2005.05.002
[22]	Billington, P.L. (1987) The Classic Economic Production Quantity Model with Set up Cost as a Function of Capital Expenditure. Decision Series, 18, 25-42. http://dx.doi.org/10.1111/j.1540-5915.1987.tb01501.x
[23]	Pakkala, T.P.M. and Achary, K.K. (1992) A Deterministic Inventory Model for Deteriorating Items with Two Warehouses and Finite Replenishment Rate. European Journal of Operational Research, 57, 71-76. http://dx.doi.org/10.1016/0377-2217(92)90306-T
[24]	Abad, P.L. (1996) Optimal Pricing and Lot Sizing under Conditions of Perish ability and Partial Backordering. Management Science, 42, 1093-1104. http://dx.doi.org/10.1287/mnsc.42.8.1093
[25]	Singh, T. and Pattnayak, H. (2013) An EOQ Model for Deteriorating Items with Linear Demand, Variable Deterioration and Partial Backlogging. Journal of Service Science and Management, 6, 186-190. http://dx.doi.org/10.4236/jssm.2013.62019
[26]	Singh, T. and Pattnayak, H. (2012) An EOQ Model for a Deteriorating Item with Time Dependent Exponentially Declining Demand under Permissible Delay in Payment. IOSR Journal of Mathematics, 2, 30-37. http://dx.doi.org/10.9790/5728-0223037
[27]	Singh, T. and Pattnayak, H. (2013) An EOQ Model for a Deteriorating Item with Time Dependent Quadratic Demand and Variable Deterioration under Permissible Delay in Payment. Applied Mathematical Science, 7, 2939-2951.
[28]	Amutha, R. and Chandrasekaran, E. (2013) An EOQ Model for Deteriorating Items with Quadratic Demand and Tie Dependent Holding Cost. International Journal of Emerging Science and Engineering, 1, 5-6.
[29]	Ouyang, W. and Cheng, X. (2005) An Inventory Model for Deteriorating Items with Exponential Declining Demand and Partial Backlogging. Yugoslav Journal of Operation Research, 15, 277-288. http://dx.doi.org/10.2298/YJOR0502277O
[30]	Dave, U. and Patel, L.K. (1981) Policy Inventory Model for Deteriorating Items with Time Proportional Demand. Journal of the Operational Research Society, 32, 137-142.