1. Introduction
Circular data refer to a set of observations measured by angles and distributed within 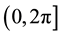 radians and it can be presented on the circumference of a unit circle. Circular data need special statistical methods to be described and modeled rather than the conventional linear techniques. Circular data can be found whenever periodic phenomena occur; it is the source of interest to scientists in many fields, including: biology, meteorology, physics, psychology, image analysis, medicine, astronomy, social sciences and earth sciences, see [1] . The existence of outliers is considered as one of the most common problems in statistical analysis. This can be extended to circular data due to the expected influence of outliers on the parameters estimates. Outliers in the context of circular data would be defined as a set of observations which is inconsistent with the rest of the sample. It is expected to lie far from the mean direction of the circular sample. Despite this, there are only a few numerical and graphical tests of discordancy in circular samples. The problem of outliers in different types of circular data including univariate samples, regression, functional relationship models and circular time series are addressed by several authors (see [2] -[7] ).
radians and it can be presented on the circumference of a unit circle. Circular data need special statistical methods to be described and modeled rather than the conventional linear techniques. Circular data can be found whenever periodic phenomena occur; it is the source of interest to scientists in many fields, including: biology, meteorology, physics, psychology, image analysis, medicine, astronomy, social sciences and earth sciences, see [1] . The existence of outliers is considered as one of the most common problems in statistical analysis. This can be extended to circular data due to the expected influence of outliers on the parameters estimates. Outliers in the context of circular data would be defined as a set of observations which is inconsistent with the rest of the sample. It is expected to lie far from the mean direction of the circular sample. Despite this, there are only a few numerical and graphical tests of discordancy in circular samples. The problem of outliers in different types of circular data including univariate samples, regression, functional relationship models and circular time series are addressed by several authors (see [2] -[7] ).
The rest of this paper is organized as follows: Section 2 describes the properties of the wrapped Cauchy distribution. Section 3 presents four discordance tests to detect possible outliers in circular univariate data. In Section 4, the cut-off points for tests are obtained based on samples generated from the wrapped Cauchy distribution. The power of performances is investigated via simulation studies in Section 5. Lastly, we apply the statistics on two real data sets for illustration in Section 6.
2. Wrapped Cauchy Distribution
A circular random variable 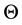 can be obtained from any random variable on the real line X with probability density function
can be obtained from any random variable on the real line X with probability density function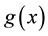 , and distribution function
, and distribution function 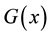 by defining
by defining
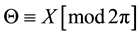 .
.
That’s mean wrapping the original distribution on the real line around the circle to get the wrapped distribution. The Cauchy distribution on the real line with the density
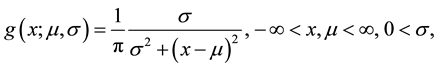 (1)
(1)
where 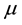 and
and 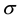 are the mean and standard deviation, respectively. Once we wrapped the
are the mean and standard deviation, respectively. Once we wrapped the 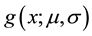 around the circle, then we get to the wrapped Cauchy distribution with probability density function denoted by
around the circle, then we get to the wrapped Cauchy distribution with probability density function denoted by 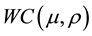 and given by:
and given by:
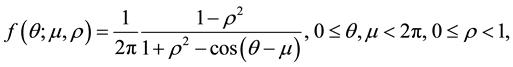 (2)
(2)
where 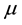 is the mean direction and
is the mean direction and 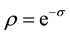 is the concentration parameter that is called the mean resultant length. Then, the distribution function of the wrapped Cauchy is given by:
is the concentration parameter that is called the mean resultant length. Then, the distribution function of the wrapped Cauchy is given by:
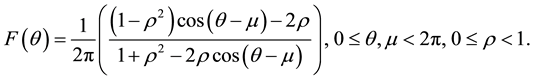
Reference [8] introduced the wrapped Cauchy distribution, and [9] illustrated that the wrapped Cauchy distribution can be obtained by mapping Cauchy distribution on to the circle by the transformation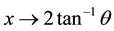 . Reference [10] quantified the dispersion measure
. Reference [10] quantified the dispersion measure 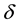 for the wrapped Cauchy distribution by a concentration
for the wrapped Cauchy distribution by a concentration
parameter![]() , and is given in the form
, and is given in the form![]() , and he explained that as
, and he explained that as ![]() approaches 0, the distribution converges to the circular uniform distribution
approaches 0, the distribution converges to the circular uniform distribution ![]() with probability density function
with probability density function![]() ;
;
and as ![]() approaches one, the distribution tends to the point distribution concentrated in the direction
approaches one, the distribution tends to the point distribution concentrated in the direction![]() .
.
The ![]() distribution is unimodal and symmetric about
distribution is unimodal and symmetric about![]() , Reference [11] illustrated that the
, Reference [11] illustrated that the ![]() distribution enjoys the additive property and the central limit theorem, on other words, the convolution of the wrapped Cauchy distributions
distribution enjoys the additive property and the central limit theorem, on other words, the convolution of the wrapped Cauchy distributions ![]() and
and ![]() is the wrapped Cauchy distribution
is the wrapped Cauchy distribution![]() . One of the main features of the wrapped Cauchy distribution that has a heavy tail even for large concentrations, which make the detection of outlier a hard task.
. One of the main features of the wrapped Cauchy distribution that has a heavy tail even for large concentrations, which make the detection of outlier a hard task.
3. Discordance Tests for Circular Samples
Suppose that we are given angles ![]() that are observations in a random circular sample of size
that are observations in a random circular sample of size ![]() from a circular population. We consider four discordance tests based on M, C, D, and A statistics to identify outliers in a univariate circular sample from the WC distribution. Under the null hypothesis that
from a circular population. We consider four discordance tests based on M, C, D, and A statistics to identify outliers in a univariate circular sample from the WC distribution. Under the null hypothesis that ![]() is not an outlier.
is not an outlier.
3.1. M Statistic
The statistic was proposed by [12] and given in the following formulation, ![]() , where
, where
![]() is the resultant length and such that
is the resultant length and such that ![]() and
and![]() , and
, and ![]() is the resultant length by excluding the ith observation. Reference [2] approximated the asymptotic distribution of the
is the resultant length by excluding the ith observation. Reference [2] approximated the asymptotic distribution of the ![]() statistic for large values of the concentration parameter by a standard normal distribution after reformulation of the M statistic in terms of:
statistic for large values of the concentration parameter by a standard normal distribution after reformulation of the M statistic in terms of:
![]() (3)
(3)
where![]() .
.
3.2. C Statistic
It was proposed by [2] , and given by
![]() (4)
(4)
where ![]() is the mean resultant length of circular data set and
is the mean resultant length of circular data set and ![]() is the mean resultant length by excluding the ith observation.
is the mean resultant length by excluding the ith observation.
3.3. D Statistic
It was derived based on the relative arc lengths between the ordered observations of a circular sample where![]() . Let
. Let ![]() be the arc length between consecutive observations and defined by
be the arc length between consecutive observations and defined by![]() ,
,
![]() and
and![]() . Define
. Define![]() ,
, ![]() and
and![]() . Let
. Let ![]() corresponds
corresponds
to the greatest arc containing a single observation![]() . The
. The ![]() is two tailed statistic, therefore, [2] suggested the consideration of the minimum value of
is two tailed statistic, therefore, [2] suggested the consideration of the minimum value of ![]() and its inverse
and its inverse![]() , where
, where![]() .
.
3.4. A Statistic
Reference [13] defined the circular distance between two angles ![]() and
and ![]() as
as![]() . Recently, [14]
. Recently, [14]
proposed a new test based on the summation of all circular distances ![]()
from the point of interest ![]() to all other points
to all other points![]() ,
, ![]() and given in the form
and given in the form
![]() (5)
(5)
Furthermore, the approximated distribution of the A statistic was discussed in [15] .
For the mentioned four tests of discordancy the cut-off points at three percentiles 10%, 5% and 1% are obtained based on simulation studies for samples generated from von Mises distribution with various sample sizes and concentration parameters, and also for the wrapped normal distribution (see [5] ). The values of statistics are then compared with the associated cut-off points, if the value of statistics is greater than the cut-off point, then the null hypothesis is rejected and the observation is labeled as an outlier.
4. Cut-Off Points of the Discordance Tests
In this section, we obtain the cut-off points for the four test statistics based on simulation studies. The percentage points of the null distribution of free outliers in the generated random circular samples from the wrapped Cauchy distribution, with mean direction zero and concentration parameter![]() ,
,![]() . We consider 12 values of the concentration parameter
. We consider 12 values of the concentration parameter ![]() in the range of 0.1 to 0.999 and 20 different sample sizes from 5 to 150. For each generated random sample the values of the four considered statistics M, C, D and A are calculated based on the formulas in Section 3.
in the range of 0.1 to 0.999 and 20 different sample sizes from 5 to 150. For each generated random sample the values of the four considered statistics M, C, D and A are calculated based on the formulas in Section 3.
For each combination of the sample size n and concentration parameter![]() , the process is repeated 3000 times to ensure the convergence of the desired percentiles (cut-off points). The obtained statistics are sorted in ascending manner and then 10%, 5% and 1% upper percentiles of free outliers samples are obtained. Tables 1-4
, the process is repeated 3000 times to ensure the convergence of the desired percentiles (cut-off points). The obtained statistics are sorted in ascending manner and then 10%, 5% and 1% upper percentiles of free outliers samples are obtained. Tables 1-4
![]()
Table 1. The 5th percentile cut-off points for the test based on the M statistic.
![]()
Table 2. The 5th percentile cut-off points for the test based on the C statistic.
![]()
Table 3. The 5th percentile cut-off points for the test based on the D statistic.
![]()
Table 4. The 5th percentile cut-off points for the test based on the A statistic.
present part of the cut-off points at 5% percentiles. The comprehensive cut-off points are available upon request from the authors. From the obtained cut-off points we notice that:
Firstly, as one would expect, there are an inverse relationship between the cut-off points and the level of percentiles. Secondly, for M statistic the increase of the concentration parameter ![]() increases the cut-off of points, while the increase the sample size n decreases the cut-off points. Thirdly, the cut-off points of D statistic are fluctuating slightly for
increases the cut-off of points, while the increase the sample size n decreases the cut-off points. Thirdly, the cut-off points of D statistic are fluctuating slightly for![]() , and correlated indirectly with either sample size n or concentration parameter
, and correlated indirectly with either sample size n or concentration parameter ![]() for
for![]() . Fourthly, for C statistic the cut-off points are a decreasing function of the concentration parameter
. Fourthly, for C statistic the cut-off points are a decreasing function of the concentration parameter ![]() and there are an inverse relationship between the cut-off points and the sample size. Lastly, the cut-off points of A statistic keep increasing as the concentration parameter increase up to
and there are an inverse relationship between the cut-off points and the sample size. Lastly, the cut-off points of A statistic keep increasing as the concentration parameter increase up to![]() , and then the cut-off points are rapidly approach zero for
, and then the cut-off points are rapidly approach zero for![]() . Furthermore, the increase of sample size reflects on the concentration parameters as follows: 1) for small concentration parameter
. Furthermore, the increase of sample size reflects on the concentration parameters as follows: 1) for small concentration parameter ![]() the cut-off points decreases gradually; 2) for
the cut-off points decreases gradually; 2) for ![]() the cut-off points almost constant; 3) for high concentration parameter
the cut-off points almost constant; 3) for high concentration parameter ![]() the cut-off points increases gradually.
the cut-off points increases gradually.
5. Performance of the Discordance Tests
The power of performance of discordancy tests can be evaluated via several measures. References [16] [17] stated that a good test of discordancy should have: 1) a high power function; ![]() where
where ![]() is the Type-II error; 2) a high probability of identifying a contaminating value as an outlier when it is in fact an extreme value, where an extreme value is defined as a point with the maximum circular deviation, denoted by
is the Type-II error; 2) a high probability of identifying a contaminating value as an outlier when it is in fact an extreme value, where an extreme value is defined as a point with the maximum circular deviation, denoted by![]() ; and 3) a low probability of wrongly identifying a good observation as discordant, where
; and 3) a low probability of wrongly identifying a good observation as discordant, where![]() .
.
To study the performances of the four discordancy tests, we use 3000 samples based on different sizes n and concentration parameter![]() . The samples are generated in such a way that
. The samples are generated in such a way that ![]() of the observations come from
of the observations come from ![]() and the remaining one observation comes from
and the remaining one observation comes from![]() , where
, where ![]() is the degree of contamination and
is the degree of contamination and![]() . The M, C, D, and A statistics in each random sample are then calculated based on corresponding equations as given in Section 3. Furthermore, the values of power performances are obtained.
. The M, C, D, and A statistics in each random sample are then calculated based on corresponding equations as given in Section 3. Furthermore, the values of power performances are obtained.
Figure 1 illustrates the behavior of power of performances of the tests for different cases. The main results can be summarized as follows:
Firstly, the performance for all statistics increases when we increase the contamination value ![]() (Figure 1(a) and Figure 1(d)) and tests outperform for
(Figure 1(a) and Figure 1(d)) and tests outperform for ![]() (Figure 1(c) and Figure 1(d)). C and A statistics perform better than other statistics for large contamination levels
(Figure 1(c) and Figure 1(d)). C and A statistics perform better than other statistics for large contamination levels![]() , while M statistic is better for small contamination level
, while M statistic is better for small contamination level![]() . Secondly, there is an increasing function between the power of performances and the concentration parameter (see Figure 1(a) and Figure 1(c)). Thirdly: For any sample size, all considered discordancy tests at moderate or less concentration parameter
. Secondly, there is an increasing function between the power of performances and the concentration parameter (see Figure 1(a) and Figure 1(c)). Thirdly: For any sample size, all considered discordancy tests at moderate or less concentration parameter![]() , the values of P1 are very low (less than 0.1) regardless the contamination level
, the values of P1 are very low (less than 0.1) regardless the contamination level ![]() (Figure 1(a) and Figure 1(b)). The weak performances for small concentration parameter
(Figure 1(a) and Figure 1(b)). The weak performances for small concentration parameter ![]() is attributed to heavily tails of the wrapped Cauchy distribution, similar trends are observed for P3 and P5. Lastly, the difference between P1 and P3 generally are very closes to 0 for all cases.
is attributed to heavily tails of the wrapped Cauchy distribution, similar trends are observed for P3 and P5. Lastly, the difference between P1 and P3 generally are very closes to 0 for all cases.
6. Real Data Analysis
For illustration purposes, two real data sets following the wrapped Cauchy distribution are considered to be analyzed, and to apply the proposed tests of discordancy to illustrate their performance in real data as given in the following subsections.
6.1. The Ants’ Direction Data
Reference [10] randomly selected the directions chosen by 100 ants toward a black target when they are released in a round arena as a part from a study conducted by [18] . The wrapped Cauchy distribution has been shown to be the best distribution for the data [19] . The estimates of location parameters, namely circular mean and median are 183˚ and 180˚, respectively. Which are close to each other and reflects the symmetry of the data distribution. Two measures of dispersion inform that the data are moderately concentrated, where the estimates of mean resultant length and concentration parameter are 0.61 and 0.65 respectively.
Table 5 gives the actual values of each test statistics, the corresponding cut-off points for ![]() and
and![]() , associated with the decision. None of the tests values is exceeded the associated cut-off points, thus we may conclude that the ant’s direction data set is free of any outliers.
, associated with the decision. None of the tests values is exceeded the associated cut-off points, thus we may conclude that the ant’s direction data set is free of any outliers.
![]()
Figure 1. Relative performances of discordancy tests for wrapped Cauchy distribution.
![]()
Table 5. Results of discordancy tests on ants’ direction data.
6.2. Wind Data
It consists of the wind direction at 6 a.m. and 12 noon were measured each day at the weather station in Milwaukee for 21 consecutive days. Reference [20] proposed a circular-circular regression model with error follow the wrapped Cauchy distribution. The curve is expressed as a form of the Mȍbius circle transformation. As an example, [20] used their model for regressing this data at 12 noon on that at 6 a.m. The maximum likelihood estimates of the parameters are ![]() and
and![]() . The circular error that obtained from the circular regression model is consisted of 21 observations measured in radian and presented in Figure 2.
. The circular error that obtained from the circular regression model is consisted of 21 observations measured in radian and presented in Figure 2.
The circular mean and median of circular error is very close to zero (−0.04) and 0.031, respectively, and the estimate of the mean resultant length and concentration parameter are 0.552 and 0.773 respectively. Reference [20] considered observations number 5, 7, 12, 17 and 20 as outliers without using any discordance test, and they stated that “Apart from five outliers, the proposed model seems to provide a satisfactory fit to the data”. We have implemented four discordancy tests M, C, D, and A to test whether the suspected five observations are outliers or not.
Table 6 presents the actual values of the discordancy test statistics, their corresponding cut-off point and the decision, for ![]() and
and![]() . Results show that in the first iteration, C statistic was able to detect observation number 5 with value 3.44 as an outlier, while other tests failed to identify any point as outlier.
. Results show that in the first iteration, C statistic was able to detect observation number 5 with value 3.44 as an outlier, while other tests failed to identify any point as outlier.
In order to detect any other outliers, observation number 5 is excluded and the descriptive statistics are re-estimated, the mean of circular error is −0.015 which gets closer to zero and the estimates of the mean resultant length and concentration parameter are 0.62 and 0.8 respectively. Then, the four tests of discordancy are obtained as given in the second iteration in Table 6, for ![]() at 0.05 level of significance. The four tests of discordancy agreed to identify observation number 17 as a suspected outlying observation but none of them identified it as an outlier where the tests values are less than the corresponding cut-off points.
at 0.05 level of significance. The four tests of discordancy agreed to identify observation number 17 as a suspected outlying observation but none of them identified it as an outlier where the tests values are less than the corresponding cut-off points.
![]()
Figure 2. Circular plot of circular error of the wind data.
![]()
Table 6. Results of discordancy tests on wind data.
7. Conclusion
In this paper four tests of discordancy M, C, D and A were extended for the wrapped Cauchy distribution; the cut-off points and the power of performances were investigated via extensive simulation study. It was noticed that for any sample size, all considered discordancy tests at moderate or less concentration parameter (![]() ), the power of performances is very low (less than 0.1) regardless the contamination level λ due to the heavy tailed characteristics of the wrapped Cauchy distribution. Thus, it is recommended to propose various circular regression and functional relationship models with wrapped Cauchy error which is expected to be more robust to the existence of outliers. Moreover, the tests were applied on ants’ data set and wind direction data set.
), the power of performances is very low (less than 0.1) regardless the contamination level λ due to the heavy tailed characteristics of the wrapped Cauchy distribution. Thus, it is recommended to propose various circular regression and functional relationship models with wrapped Cauchy error which is expected to be more robust to the existence of outliers. Moreover, the tests were applied on ants’ data set and wind direction data set.