1. Introduction
As is well known that solitary wave solutions of nonlinear evolution equations play an important role in nonlinear science fields, especially in nonlinear physical science, since they can provide much physical information and more insight into the physical aspects of the problem and thus lead to further applications [1] . In this paper, we will consider the Benjamin Ono (BO) equation
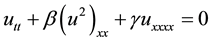
where  and
and  are non-zero constants. The BO equation is one of the important nonlinear model in physics [2] [3] . By means of traveling wave method, the exact solutions of the BO equation were obtained. Using the F-expansion method and the Jacobi elliptic function expansion method to the BO equation, a series of periodic wave solutions were got [4] . Based on an improved projective Riccat equation method, the traveling wave solutions of single variable were found [5] . Applying the bilinear method and extended homoclinic test approach [6] -[10] , periodic solitary wave and doubly periodic solutions for the BO equation were obtained [11] .
are non-zero constants. The BO equation is one of the important nonlinear model in physics [2] [3] . By means of traveling wave method, the exact solutions of the BO equation were obtained. Using the F-expansion method and the Jacobi elliptic function expansion method to the BO equation, a series of periodic wave solutions were got [4] . Based on an improved projective Riccat equation method, the traveling wave solutions of single variable were found [5] . Applying the bilinear method and extended homoclinic test approach [6] -[10] , periodic solitary wave and doubly periodic solutions for the BO equation were obtained [11] .
In recent years, rogue waves, as a special type of nonlinear waves and also known as freak waves, monster waves, killer waves, extreme waves, abnormal waves [12] , have triggered much interest in various physical branches. Rouge wave is a kind of wave that seems abnormal which is first served in the deep ocean. It always has two to three times amplitude higher than its surrounding waves and generally forms in a short time for which people think that it comes from nowhere. Rouge waves have been the subject of intensive research in oceanography [13] [14] , optical fibers [15] -[17] , superfluids [18] , Bose-Einstein condensates, financial markets and other related fields [19] -[22] . In this work, we will apply the homoclinic (hateroclinic) breather limit method (HBLM) [23] , to seek rogue wave solution of the BO equation. We take the following four steps:
Step 1
By Painleve analysis, a transformation 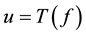 is made for some new and unknown function f.
is made for some new and unknown function f.
Step 2
By using the transformation in step 1, original equation can be converted into Hirota’s bilinear form 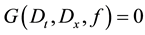 , where the D-operator [24] is defined by
, where the D-operator [24] is defined by

Step 3
Solve the above equation to get homoclinic (heteroclinic) breather wave solution by using extended homoclinic test approach (EHTA) [25] .
Step 4
Let the period of periodic wave go to infinite in homoclinic (heteroclinic) breather wave solution, we can Obtain a rational homoclinic (heteroclinic) wave and this wave is just a rouge wave.
2. Rational Breather Wave (Rogue Wave)
The BO equation,
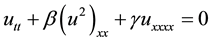 (1)
(1)
By Painleve analysis, let
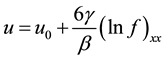 (2)
(2)
where 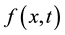 is unknown real function, and
is unknown real function, and  is the small perturbation parameter. Substituting (2) into (1) will get the following equation:
is the small perturbation parameter. Substituting (2) into (1) will get the following equation:
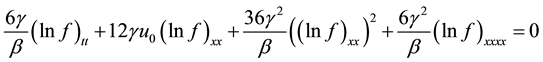 (3)
(3)
By means of the hirota bilinear operator, which is defined by
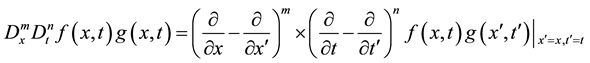 (4)
(4)
we will get
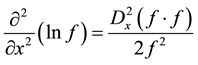 (5)
(5)
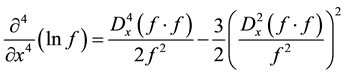 (6)
(6)
Putting (5) (6) into (3) implies the following bilinear equation:
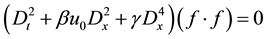 (7)
(7)
In this case we choose extended homoclinic test function
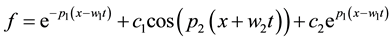 (8)
(8)
where p1, p2, w1, w2, c1 and c2 are real constants to be determined.
Substituting Equation (8) into (7), collecting coefficients of the terms![]() ,
, ![]() ,
, ![]() ,
, ![]() and the constant, and let coefficients of these terms to zero, we get an algebraic equation
and the constant, and let coefficients of these terms to zero, we get an algebraic equation
![]() (9)
(9)
Solving Equation (9), then taking![]() , we have
, we have
![]() (10)
(10)
where w1, w2, c2 are some free real constants. Choosing ![]() and
and![]() , we get from(10)
, we get from(10)![]() .
.
Substituting (10) into (8), we get
![]() (11)
(11)
where![]() ,
, ![]() ,
,![]() . Substituting (11) into (2) yields the solutions of (1) as follows, respectively
. Substituting (11) into (2) yields the solutions of (1) as follows, respectively
![]() (12)
(12)
![]() (13)
(13)
The solution ![]() (or
(or![]() ) shows a new family of two-wave, breather solitary wave, which is a solitary wave and also is a periodic wave.
) shows a new family of two-wave, breather solitary wave, which is a solitary wave and also is a periodic wave.
Substituting ![]() into the solution
into the solution![]() , it can be rewritten as follows
, it can be rewritten as follows
![]() (14)
(14)
where ![]() (see Figure 1).
(see Figure 1).
Now we consider a limit behavior of ![]() as the period
as the period ![]() of periodic wave
of periodic wave ![]() goes to infinite, i.e.
goes to infinite, i.e.![]() . By computing, we get the following result
. By computing, we get the following result
![]() (15)
(15)
where![]() , and
, and ![]() and
and ![]() as
as ![]() (see Figure 2).
(see Figure 2).
Especially, if let![]() , we will get
, we will get![]() , so the two breather wave solution can not be obtained, meanwhile, the rational breather wave solution (rogue wave solution) can’t also be find. The small perturbation parameter
, so the two breather wave solution can not be obtained, meanwhile, the rational breather wave solution (rogue wave solution) can’t also be find. The small perturbation parameter ![]() plays a huge part in finding rouge wave solution.
plays a huge part in finding rouge wave solution.
Equation (15) is a rational solution of Equation (1), and it is also a breather-type solution. ![]() for fixed t as
for fixed t as![]() . So, the solution
. So, the solution ![]() is a rogue wave solution which has two to three times amplitude higher than its surrounding waves and forms in a short time. One may think that whether the energy collection and superposition of breather solitary wave in many periods lead to a rogue wave or not.
is a rogue wave solution which has two to three times amplitude higher than its surrounding waves and forms in a short time. One may think that whether the energy collection and superposition of breather solitary wave in many periods lead to a rogue wave or not.
3. Conclusion
In the paper, we apply the homoclinic (hateroclinic) breather limit method (HBLM) to find the BO equation’s breather solitary solution and rational breather solution. Meanwhile, rational breather solution obtained here is just a rogue wave solution of the BO equation. Furthermore, the small perturbation parameter u0 plays an important role in seeking rouge wave solution too. Next, we will try to use some methods to look for multi-rogue waves, such as the two-order wronskian determinant, Darboux transformation and so on.
Acknowledgements
The authors are grateful to the referee for a number of helpful suggestions to improve the paper.