Erratum to “Weierstrass’ Elliptic Function Solution to the Autonomous Limit of the String Equation of Type (2,5)” [Advances in Pure Mathematics 4 (2014), 494-497]

Yoshikatsu Sasaki^1*

¹Department of Mathematics, Hiroshima University, Higashi-Hiroshima, Japan.

DOI: 10.4236/apm.2014.412077                

Abstract

In this note, we analyze a few major claims about . As a consequence, we rewrite a major theorem, nullify its proof and one remark of importance, and offer a valid proof for it. The most important gift of this paper is probably the reasoning involved in all: We observe that a constant, namely t, has been changed into a variable, and we then tell why such a move could not have been made, we observe the discrepancy between the claimed domain and the actual domain of a supposed function that is created and we then explain why such a function could not, or should not, have been created, along with others.

Keywords

Painlevé Hierarchy, String Equation, Elliptic Function

P. 494, L. 7-: The string equation of type (q, p) should be correctly read as

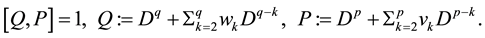
P. 496, L. 13 - 14: Theorem B should be correctly read as follows:

Theorem B. The autonomous limit Equation (A) has a solution concretely described by the Weierstrass’ elliptic function as

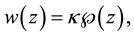
where 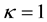or 3.

P. 496, L. 17: In Remark, g₂ and g₃ in the elliptic function theory should be correctly read as follows:

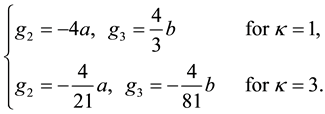
P. 496, L. 21: In the r.h.s. of Equation (1), “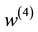” should be correctly read as “”.

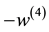P. 496, L. 3- - P. 497, L. 2: These 5 lines should be correctly read as follows:

If both of (2) and (3) are valid, then 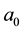must vanish and 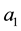coincides with 4 or.

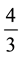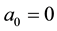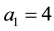Case and: In this case, we immediately obtain, ,

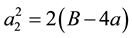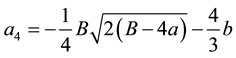, where 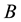is a root of. Inversely, if these are sa-

tisfied, both of (2) and (3) are valid. 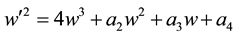can be reduced to by

. But, for brevity, now we put, and then, , i.e.

. Here and. The irrational equation satisfied by determines the

integral constant in the r.h.s. of (2) as.

Case and: In this case, we easily obtain, ,. Only is

allowed as the integral constant c in the r.h.s. of (2). Inversely, if these are satisfied, both of (2) and (3) are valid.

is reduced to by w = 3v, and then and. □

Conflicts of Interest

The authors declare no conflicts of interest.

References

[1]	Douglas, M.R. (1990) String in Less than One-Dimensions and K-dV Hierarchies. Physics Letters B, 238, 176-180. http://dx.doi.org/10.1016/0370-2693(90)91716-O
[2]	Moore, G. (1990) Geometry of the String Equations. Communications in Mathematical Physics, 133, 261-304. http://dx.doi.org/10.1007/BF02097368
[3]	Moore, G. (1991) Matrix Models of 2D Gravity and Isomonodromic Deformations. Progress of Theoretical Physics Supplement, 102, 255-285. http://dx.doi.org/10.1143/PTPS.102.255
[4]	Fukuma, M., Kawai, H. and Nakayama, R. (1991) Infinite Dimensional Grassmannian Structure of Two Dimensional String Theory. Communications in Mathematical Physics, 143, 371-403. http://dx.doi.org/10.1007/BF02099014
[5]	Kac, V. and Schwarz, A. (1991) Geometric Interpretation of Partition Functions of 2D Gravity. Physics Letters B, 257, 329-334. http://dx.doi.org/10.1016/0370-2693(91)91901-7
[6]	Schwarz, A. (1991) On Solutions to the String Equations. Modern Physics Letters A, 29, 2713-2725. http://dx.doi.org/10.1142/S0217732391003171
[7]	Adler, M. and van Moerbeke, P. (1992) A Matrix Integral Solution to Two-Dimensional Wp-Gravity. Communications in Mathematical Physics, 147, 25-26. http://dx.doi.org/10.1007/BF02099527
[8]	van Moerbeke, P. (1994) Integrable Foudations of String Theory. In: Babelon, O., et al., Ed., Lectures on Integrable Systems, World Science Publisher, Singapore, 163-267.
[9]	Takasaki, K. (2007) Hamiltonian Structure of PI Hierarchy. SIGMA, 3, 42-116.
[10]	Ince, E.L. (1956) Ordinary Differential Equations. Dover Publications, New York.
[11]	Conte, R. and Mussette, M. (2008) The Painlevé Handbook. Springer Science + Business Media B.V., Dordrecht.
[12]	Weiss, J. (1984) On Classes of Integrable Systems and the Painlevé Property. Journal of Mathematical Physics, 25, 13-24. http://dx.doi.org/10.1063/1.526009
[13]	Kudryashov, N.A. (1997) The First and Second Painlevé Equations of Higher Order and Some Relations between Them. Physics Letters A, 224, 353-360. http://dx.doi.org/10.1016/S0375-9601(96)00795-5
[14]	Gromak, V.I., Laine, I. and Shimomura, S. (2002) Painlevé Differential Equations in the Complex Plane. Walter de Gruyter, Berlin. http://dx.doi.org/10.1515/9783110198096
[15]	Shimomura, S. (2004) Poles and α-Points of Meromorphic Solutions of the First Painlevé Hierarchy. Publications of the Research Institute for Mathematical Sciences, Kyoto University, 40, 471-485. http://dx.doi.org/10.2977/prims/1145475811
[16]	Kimura, H. (1989) The Degeneration of the Two Dimensional Garnier System and the Polynomial Hamiltonian Structure. Annali di Matematica Pura ed Applicata, 155, 25-74. http://dx.doi.org/10.1007/BF01765933
[17]	Suzuki, M. (2006) Spaces of Initial Conditions of Garnier System and Its Degenerate Systems in Two Variables. Journal of the Mathematical Society of Japan, 58, 1079-1117. http://dx.doi.org/10.2969/jmsj/1179759538
[18]	Shimomura, S. (2000) Painlevé Property of a Degenerate Garnier System of (9/2)-Type and a Certain Fourth Order Non-Linear Ordinary Differential Equation. Annali della Scuola Normale Superiore di Pisa, Classe di Scienze, 29, 1-17.