Linear Dependence of Balances for Non-Redox Electrolytic Systems ()
1. Introduction
In numerous examples of electrolytic redox systems presented in our previous papers [1] -[4] , it was found that the linear combination 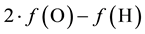 of elemental balances:
of elemental balances: 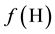 for H and
for H and 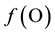 for O jest is linearly independent on charge and elemental/core balances for elements/cores different from H and O. This linear independence proves that
for O jest is linearly independent on charge and elemental/core balances for elements/cores different from H and O. This linear independence proves that  is a new equation, considered as the starting form of the electron balance (GEB) related to the redox system in question. In this way it has been shown, inter alia, that the simplest form of GEB related to a redox system in mixed-solvent media is the same, regardless the solvent composition―assuming that the solutes do not form with solvents other species (except those known from aqueous media) besides solvates [5] -[7] .
is a new equation, considered as the starting form of the electron balance (GEB) related to the redox system in question. In this way it has been shown, inter alia, that the simplest form of GEB related to a redox system in mixed-solvent media is the same, regardless the solvent composition―assuming that the solutes do not form with solvents other species (except those known from aqueous media) besides solvates [5] -[7] .
For non-redox systems, it was stated that the linear combination  is linearly dependent on charge and elemental/core balances for elements/cores ≠ H, O. This can easily be stated by transformation of the linear combination of the relevant equations to the identity, 0 = 0. In this work, this kind of transformation will be applied to two relatively complex systems involved with 1) determination of cyanide according to Liebig- Denigès method [8] and 2) complexometric titration of zinc with EDTA [9] .
is linearly dependent on charge and elemental/core balances for elements/cores ≠ H, O. This can easily be stated by transformation of the linear combination of the relevant equations to the identity, 0 = 0. In this work, this kind of transformation will be applied to two relatively complex systems involved with 1) determination of cyanide according to Liebig- Denigès method [8] and 2) complexometric titration of zinc with EDTA [9] .
2. Liebig-Denigès Method of Cyanide Determination
In the system involved with Liebig-Denigès method, V mL of the solution composed of AgNO3 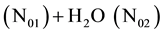 is added into
is added into 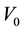 mL of the solution composed of
mL of the solution composed of 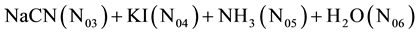
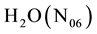 . At defined stage of the process, the following species are present in the system:
. At defined stage of the process, the following species are present in the system:
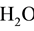 (N1),
(N1), 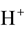 (N2),
(N2),  (N3, n3),
(N3, n3), 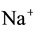 (N4, n4),
(N4, n4), ![]() (N5, n5),
(N5, n5), ![]() (N6, n6),
(N6, n6), ![]() (N7, n7),
(N7, n7), ![]() (N8, n8),
(N8, n8), ![]() (N9, n9), NH3 (N11, n11), Ag+ (N12, n12), AgOH (N13, n13),
(N9, n9), NH3 (N11, n11), Ag+ (N12, n12), AgOH (N13, n13), ![]() (N14, n14),
(N14, n14), ![]() (N15, n15),
(N15, n15), ![]() (N16, n16),
(N16, n16), ![]() (N17, n17),
(N17, n17), ![]() (N18, n18), AgI (N19, n19),
(N18, n18), AgI (N19, n19), ![]() (N21, n21),
(N21, n21), ![]() (N22, n22),
(N22, n22), ![]() (N23, n23),
(N23, n23), ![]() (N24, n24),
(N24, n24), ![]() (N25, n25),
(N25, n25), ![]() (N26, n26),
(N26, n26), ![]() (N27, n27).
(N27, n27).
From the balances:
・ ![]()
![]() (1)
(1)
・ ![]()
![]() (2)
(2)
we have
・ ![]()
![]() (3)
(3)
Addition of (3) to charge balance (4) and balances: f(Na) (5), f(K) (6), 5 f(NO3) (7), f(CN) (8), 3f(NH3) (9), f(Ag) (10) and f(I) (11)
![]() (4)
(4)
![]() (5)
(5)
![]() (6)
(6)
![]() (7)
(7)
![]() (8)
(8)
![]() (9)
(9)
![]() (10)
(10)
![]() (11)
(11)
gives the identity, 0 = 0, i.e., (3) is not an independent balance in the system. The identity is also valid before crossing the solubility product for AgI(s).
3. Complexometric Titration of Zinc with EDTA
Let us consider ![]() mL of titrand (D), containing
mL of titrand (D), containing ![]() (erio T, C0In) titrated with V mL of titrant (T) containing EDTA (C).
(erio T, C0In) titrated with V mL of titrant (T) containing EDTA (C).
The titrand is composed of N01 molecules of ZnSO4・7H2O (goslarite), N02 molecules of NH3, N03 molecules of NH4Cl, N04 molecules of NaH2In = C20H12N3O7SNa, N05 molecules of H2O and the titrant is composed of N06 molecules of EDTA = Na2H2L・2H2O = C10H14N2O8Na2・2H2O and N07 molecules of H2O, at defined point of titration (V mL of T added). In the system in question, the following species are formed:
H2O (N1), H+ (N2, n2), OH− (N3, n3), ![]() (N4, n4),
(N4, n4), ![]() (N5, n5),
(N5, n5), ![]() (N6, n6), Na+ (N7, n7),
(N6, n6), Na+ (N7, n7), ![]() (N8, n8),
(N8, n8), ![]() (N9, n9), Zn2+ (N11, n11), ZnOH+ (N12, n12), soluble complex
(N9, n9), Zn2+ (N11, n11), ZnOH+ (N12, n12), soluble complex ![]() (N13, n13),
(N13, n13), ![]() (N14, n14),
(N14, n14), ![]()
![]() (N15, n15),
(N15, n15), ![]() (N16, n16),
(N16, n16), ![]() (N17, n17),
(N17, n17), ![]() (N18, n18),
(N18, n18), ![]() (N19, n19), ZnCl+ (N21, n21); ZnSO4 (N22, n22), C20H13N3O7S (N23, n23), C20H12N3O7S− (N24, n24), C20H11N3O7S2− (N25, n25), C20H10N3O7S3− (N26, n26), C20H10N3O7SZn− (N27, n27),
(N19, n19), ZnCl+ (N21, n21); ZnSO4 (N22, n22), C20H13N3O7S (N23, n23), C20H12N3O7S− (N24, n24), C20H11N3O7S2− (N25, n25), C20H10N3O7S3− (N26, n26), C20H10N3O7SZn− (N27, n27), ![]() (N28, n28),
(N28, n28), ![]()
![]() (N29, n29),
(N29, n29), ![]()
![]() (N31, n31), C10H16N2O8
(N31, n31), C10H16N2O8 ![]() (N32, n32),
(N32, n32), ![]()
![]() (N33, n33),
(N33, n33), ![]()
![]() (N34, n34),
(N34, n34), ![]()
![]() (N35, n35),
(N35, n35), ![]()
![]() (N36, n36),
(N36, n36), ![]()
![]() (N37, n37),
(N37, n37), ![]()
![]() (N38, n38),
(N38, n38), ![]()
![]() (N39, n39).
(N39, n39).
The complex ![]() is formed in reaction between
is formed in reaction between ![]() and
and![]() . The species can be arranged in the following balances:
. The species can be arranged in the following balances:
・ ![]()
![]() (12)
(12)
・ ![]()
![]() (13)
(13)
The balance![]() , obtained from Equations (12) and (13), is as follows
, obtained from Equations (12) and (13), is as follows
![]() (14)
(14)
Addition of (14) to charge balance (15) and balances for ![]() (16),
(16), ![]() (17),
(17), ![]() (18),
(18),
![]() (19),
(19), ![]() (20),
(20), ![]() (21), and
(21), and ![]() (22):
(22):
![]() (15)
(15)
![]() (16)
(16)
![]() (17)
(17)
![]() (18)
(18)
![]() (19)
(19)
![]() (20)
(20)
![]() (21)
(21)
![]() (22)
(22)
gives the identity, 0 = 0, that testifies about linear dependence between the balances, i.e., Equation (14) is linearly dependent on other balances in the system. Note that the Equations (19)-(22) are specified separately, according to different “cores”: SO4, NH3, C20H10N3O7S, C10H12N2O8. Note that N enters the compounds and species in Equations (20)-(22); S enters the compounds and species in Equations (19) and (21); C enters the compounds and species in Equations (21) and (22). However, none transformations occur between the “cores” of the species that belong to different concentration balances. Generalizing, for any non-redox system, there are some numbers/multipliers for the relevant equations that reduce the sum received to the identity.
Referring again to Equation (21), related to the species involved with erio T, one can write the elemental balances:
![]() (for C),
(for C),
![]()
![]() (for N),
(for N), ![]() (for S),
(for S),
and
![]() (for O).
(for O).
All the equations are identical and equivalent to Equation (21), because the “core” C20H10N3O7S is unchanged in reactions occurred during the titration. Similarly, the species involved with EDTA, see Equation (22), fulfill the relations:
![]() (for C),
(for C),
and
![]() (for N).
(for N).
Both equations are equivalent to![]() .
.
4. Final Comments
Checking of linear dependence or independence of algebraic equations [10] is not a mathematical problem of the highest order. However, it requires an additional knowledge of the user, concerning the properties of the matrix ![]() (
(![]() ;
;![]() ;
;![]() ) of coefficients
) of coefficients ![]() in the matrix equation
in the matrix equation![]() , where
, where
![]() (23)
(23)
with vectors of variables, ![]() , and vector of constant terms,
, and vector of constant terms,![]() . For explaining these properties, some abstract terms such as (dimension of) vector space, (matrix, kolumn, row) ranks, are used.
. For explaining these properties, some abstract terms such as (dimension of) vector space, (matrix, kolumn, row) ranks, are used.
It should be noted, however, that the coefficients ![]() and
and ![]() used in purely algebraic equations
used in purely algebraic equations
![]() (24)
(24)
do not have specific physical or chemical connotations. Assuming the charge balance as the second of the balances (24) considered for this purpose, we state that the coefficients ![]() in this balance are involved with external charges of the species in the system in question and
in this balance are involved with external charges of the species in the system in question and ![]() in the vector
in the vector![]() . The coefficients
. The coefficients ![]() in the elemental/core balances are involved with the number of elements/cores in the related species. The coefficients in
in the elemental/core balances are involved with the number of elements/cores in the related species. The coefficients in ![]() depend on the form of equations for
depend on the form of equations for ![]() and
and![]() .
.
In this paper, the linear relationship between the balance ![]() and charge + elemental/core balances for elements/cores ¹ H, O was checked in extremely simple way (indicated in [4] ) and proved on examples of two electrolytic non-redox systems, of analytical importance, known from titrimetric analyses. Full complexity of these systems, known from preliminary physicochemical data, is involved in the related balances, expressed in terms of numbers of entities of particular components and species
and charge + elemental/core balances for elements/cores ¹ H, O was checked in extremely simple way (indicated in [4] ) and proved on examples of two electrolytic non-redox systems, of analytical importance, known from titrimetric analyses. Full complexity of these systems, known from preliminary physicochemical data, is involved in the related balances, expressed in terms of numbers of entities of particular components and species![]() . The related balances can also be expressed in terms of molar concentrations:
. The related balances can also be expressed in terms of molar concentrations: ![]()
![]() for the species
for the species ![]() (NA? Avogadro’s number) and analogous relationships for components forming the titrand (D) and titrant (T) in the related D + T system. It should be recalled and emphasized that a linear relationship between
(NA? Avogadro’s number) and analogous relationships for components forming the titrand (D) and titrant (T) in the related D + T system. It should be recalled and emphasized that a linear relationship between ![]() and charge + elemental/core balances for elements/cores ¹ H, O does not occur for redox systems, and the resulting balance is the basis of formulation of GEB for these systems, obtained according to Approach II to GEB [1] -[7] [11] .
and charge + elemental/core balances for elements/cores ¹ H, O does not occur for redox systems, and the resulting balance is the basis of formulation of GEB for these systems, obtained according to Approach II to GEB [1] -[7] [11] .
NOTES
*Corresponding author.