Performance of Suboptimal Controllers for Affine-Quadratic Problems

Ankita Sharma^*, A. J. Shaiju

Department of Mathematics, Indian Institute of Technology Madras, Chennai, India.

DOI: 10.4236/ijmnta.2014.35025                

Abstract

In this article, affine-quadratic control problems are studied. Error bounds are derived for the difference between the performance indices corresponding to the optimal and a class of suboptimal controls. In particular, it is shown that the performance of these suboptimal controls is close to that of the optimal control whenever the error in estimating the costate initial condition is small.

Keywords

Affine-Quadratic Control, Nonlinear Control, Optimal Control, Suboptimal Control

1. Introduction

One of the most active areas in control theory is optimal control and methods to find them [1] - [3] . It has a wide range of practical applications in engineering (Aerospace, Chemical, Mechanical, Electrical), science (Physics, Biology), and economics (see e.g. [4] - [7] ). Optimal control theory has been developed for linear systems ( [1] [2] [8] ) and explicit formulae for computing optimal control inputs are available. However, control of nonlinear systems is much more challenging and obtaining formulae for optimal controls seems in general not possible. This motivated researchers to study various classes of nonlinear control problems separately, and affine-qudratic problems is one such class. In a recent paper [9] , the optimal control for affine-quadratic problems is obtained in terms of the associated costate. But, in practice, it is difficult to compute the costate (at each time) as the knowledge of its terminal condition is required.

In this article, we study the affine-quadratic control problem given by ((1), (2)). We note that a method for finding the initial condition for the costate is recently proposed [10] . This allows one to compute the initial costate (at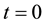) exactly or approximately. This approximation of the initial costate and the explicit formula for optimal control (as in [11] ) are shown, in this article, which give rise to suboptimal controls of practical importance. More precisely, our main theorem (Theorem 2) provides an upper bound for the difference in performance between these suboptimal and optimal control.

The article is organized as follows. In Section 2, the affine-quadratic control problem is described. We also explain how to obtain the optimal control in terms of costate. The main (Theorem 2) is proved in Section 3. This theorem provides a method to obtain the costate (without the knowledge of its terminal value) which results in an explicit formula and performance bounds for a class of suboptimal controls.

Notation: For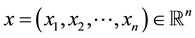, , 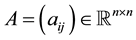and, we use the notation

, ,.

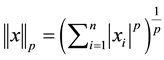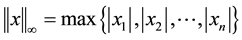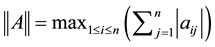2. Problem Description

We consider the affine control system

, (1)

with the quadratic cost functional

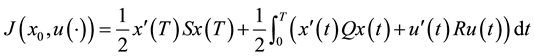. (2)

Here 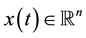is the state vector, is the control vector, ,

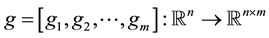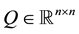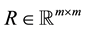, , , , and ' denotes transposition.

Throughout this paper, it is assumed that 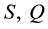are positive semidefinite, is positive definite, the functions are continuously differentiable with bounded derivatives, the control input is chosen

from the admissible control space.

Under these assumptions, for each admissible control there exist a unique solution (trajectory) of

the control system (1) denoted by.

The value function of the control problem given by (1), (2), is defined as

.

A control input is optimal (for) if

.

Similarly a control input is -optimal (for) if

.

Given, the optimal control problem is to find a control which minimizes the cost functional

. The Hamiltonian associated with the optimal control problem (1), (2), is given as

, (3)

where is the adjoint vector.

To derive an expression for the optimal control (for), it is convenient to introduce the adjoint

system:

. (4)

Here. We now state the Pontryagin’s Minimum Principle (PMP) for the affine-quadratic

control system (1), (2), which provides a set of necessary conditions for to be optimal [12] .

Theorem 1 [PMP] Let, , and. Also let be the adjoint vector

corresponding to and, as given by the equation (4). Then for a control input to be optimal

for, it is necessary that the map

,

attains minimum at, for a.e..

Corollary 1 Let, , and. Also let be the adjoint vector

corresponding to and, as given by the equation (4). Then the optimal control (for) is

. (5)

Proof. The proof follows immediately from the above theorem. □

Now to obtain (in (5)) in terms of, we solve the coupled systems given in (1) and (4)

together with the initial conditions and respectively.

In general, solving this coupled system and finding a closed form solution is very difficult. However

it may be easier to find approximately. Such an approximation will lead to the associated adjoint state

and admissible control. In the next section, we provide bounds for the

difference between the performance indices corresponding to and.

3. Performance of suboptimal controllers

In this section, we prove the main result.

Theorem 2 Consider the affine-quadratic control problem (1), (2). Let, be the optimal

control as given in (5), , and be the adjoint vector corresponding to and.

Also let be a suboptimal control and be the solution of the coupled system ((1), (4)) with

initial condition. Then

,

where

The constant depends only on the matrix function and the constant depends only on its gra- dient.

Proof. Note that

(6)

From R.H.S. of (6), we first consider the term

.

By adding and subtracting inside the integral, we get

Therefore

. (7)

From R.H.S. of (6), we next consider the term

.

In a similar manner (as for (7)), we have

. (8)

From R.H.S. of (6), we next consider the term

.

Let us have

In the above term, put the matrix as and the matrix

as for each. Then we have,

Now using assumption on the matrix function, we have that the matrix function is continuously differentiable and has bounded derivatives. Therefore

Using this and following the procedure as for the inequality (7), we get

Therefore

. (9)

Hence the result follows by the inequalities (7), (8), and (9). □

Remark 3 It follows from the previous theorem that, when.

This implies that is a good suboptimal control when is a good approximation of

. We emphasize the fact that (and hence) can be computed at each time as is known.

Conflicts of Interest

The authors declare no conflicts of interest.

References

[1]	Anderson, B.D.O. and Moore, J.B. (1989) Optimal Control: Linear Quadratic Methods. Prentice-Hall, Inc., Upper Saddle River.
[2]	Zhou, K., Doyle, J.C. and Glover, K. (1996) Robust and Optimal Control. Prentice-Hall, Inc., Upper Saddle River.
[3]	Bardi, M. and Dolcetta, I.C. (2008) Optimal Control and Viscosity Solutions of Hamilton-Jacobi-Bellman Equations. Birkhauser, Boston.
[4]	Tang, L., Zhao, L.D. and Guo, J. (2009) Research on Pricing Policies for Seasonal Goods Based on Optimal Control Theory. ICIC Express Letters, 3, 1333-1338.
[5]	Garrard, W.L. and Jordan, J.M. (1977) Design of Nonlinear Automatic Flight Control Systems. Automatica, 13, 497-505. http://dx.doi.org/10.1016/0005-1098(77)90070-X
[6]	Manousiouthakis, V. and Chmielewski, D.J. (2002) On Constrained Infinite-Time Nonlinear Optimal Control. Chemical Engineering Science, 57, 105-114. http://dx.doi.org/10.1016/S0009-2509(01)00359-1
[7]	Notsu, T., Konishi, M. and Imai, J. (2008) Optimal Water Cooling Control for Plate Rolling. International Journal of Innovative Computing, Information and Control, 4, 3169-3181.
[8]	Kalman, R.E. (1960) Contributions to the Theory of Optimal Control. Matematica Mexicana, 5, 102-119.
[9]	Effati, S. and Nik, H.S. (2011) Solving a Class of Linear and Non-Linear Optimal Control Problems by Homotopy Perturbation Method. IMA Journal of Mathematical Control and Information, 28, 539-553. http://dx.doi.org/10.1093/imamci/dnr018
[10]	Sharma, A. and Shaiju, A.J. (2014) Solution of Affine-Quadratic Control Problems. Proceedings of the 19th WC-IFAC, Cape-Town.
[11]	Jajarmi, A., Pariz, N., Kamyad, A.V. and Effati, S. (2011) A Novel Series Representation Approach to Solve a Class of Nonlinear Optimal Control Problems. International Journal of Innovative Computing, Information and Control, 7, 1413-1425.
[12]	Pontryagin, L.S., et al. (1962) The Mathematical Theory of Optimal Processes. John Wiley and Sons, Inc., New York.