1. Introduction
In this paper we use the Lewis [1] formulation of signaling and base our model on our earlier paper (Dassiou and Glycopantis [2] ), where we analysed a signaling game using a decision tree formation. The earlier paper presents a number of Bayesian equilibria and explains which one is likely to prevail using as a criterion the expected payoffs that they entail for the two players. A distinction between a true signal by a sender and a correct action by a receiver is established in terms of leading to different payoffs. A correct action by the receiver of a signal alone is not sufficient for leading to an equilibrium that involves maximum payoffs for both players. Moreover there are equilibria that do not involve maximum payoffs for either player.
Signaling games lead to the formation of language through combinations of signals and actions. In this paper we use the same signaling game as in [2] . The helper, (H), referred to also as he, stands behind a truck gesturing to the driver, (D), referred to also as she, to help her steer the truck into a narrow parking space. We assume that Nature consists of the particular position of the truck and of the parking space and that there are two such alternatives, each with probability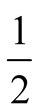 . Unlike the earlier paper, the sender is no longer fully aware of the state of nature, but rather receives a message with a noise regarding this. While both players are aware of the probabilities attached to the choices of nature,
. Unlike the earlier paper, the sender is no longer fully aware of the state of nature, but rather receives a message with a noise regarding this. While both players are aware of the probabilities attached to the choices of nature,  alone has private information (in the form of this message) and he signals to
alone has private information (in the form of this message) and he signals to  to direct her how to park her car.
to direct her how to park her car.
Lewis describes the signaling behaviour and the action that follows as a “conventional regularity” of unwritten rules of parking gestures, based on experience to which all parties conform. In terms of highest payoffs there is a common interest objective of  and
and  to get the truck into the space. In this situation they both receive their optimal payoffs.
to get the truck into the space. In this situation they both receive their optimal payoffs.
This is not always the case. A deviation from this rule, perhaps based on lack of trust, could lead to one or both of the two players getting inferior payoffs. In [2] there is a distinction between true or untrue signals sent by  and correct or incorrect actions by the driver. The issue is to investigate whether a “correct” interpretation of the signals is possible, i.e. one which would lead to an optimal payoffs equilibrium position. In such a situation no one would wish to independently change his action if all the information was revealed and moreover the payoffs would be optimal.
and correct or incorrect actions by the driver. The issue is to investigate whether a “correct” interpretation of the signals is possible, i.e. one which would lead to an optimal payoffs equilibrium position. In such a situation no one would wish to independently change his action if all the information was revealed and moreover the payoffs would be optimal.
In general, we can imagine that there are  alternative states of nature,
alternative states of nature, 
 , observed by the sender,
, observed by the sender, 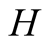 , who will send a signal concerning the private information (messages) he has received regarding the state of nature. The messages received by
, who will send a signal concerning the private information (messages) he has received regarding the state of nature. The messages received by  are not precise, but correct with a probability
are not precise, but correct with a probability  The sender compiles a set of alternative signals
The sender compiles a set of alternative signals  using a function
using a function  This is an encoding rule according to Blume [3] . The function
This is an encoding rule according to Blume [3] . The function  translates (truthfully or not) the messages regarding the states of nature into
translates (truthfully or not) the messages regarding the states of nature into  communicated signals.
communicated signals.
The receiver,  , then has to choose a response without knowing the state of nature. However he is aware of the prior probabilities of these states and the accuracy of the sender’s private information. In the sequential game,
, then has to choose a response without knowing the state of nature. However he is aware of the prior probabilities of these states and the accuracy of the sender’s private information. In the sequential game,  translates these signals (decodes according to [3] ). He chooses a best response
translates these signals (decodes according to [3] ). He chooses a best response , from alternative actions
, from alternative actions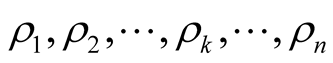 , to the signals. He applies Bayes’ rule to form a posterior assessment that the signal comes from each state of nature by setting a decoding function
, to the signals. He applies Bayes’ rule to form a posterior assessment that the signal comes from each state of nature by setting a decoding function :
: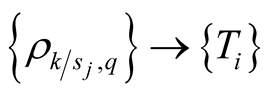 . Rubinstein [4] , notes the difficulty of formulating communication models into game theory models. Solutions in the latter are invariant to a change in the names of the actions that lead to these outcomes, i.e. alternative conventions leading to the same outcome.
. Rubinstein [4] , notes the difficulty of formulating communication models into game theory models. Solutions in the latter are invariant to a change in the names of the actions that lead to these outcomes, i.e. alternative conventions leading to the same outcome.
A characteristic of the sender-signal-receiver-action sequential game paradigm is a plethora of equilibria. This raises the question of how to choose among such equilibria. Cho and Kreps [5] propose to eliminate some of these equilibria by branding them as “unintuitive”. They restrict the out-of-equilbrium beliefs of the second party,  , i.e. interpretations that
, i.e. interpretations that  would have given to the signal that
would have given to the signal that  might have sent, but in equilibrium does not. Such beliefs might upset the given equilibrium. Cho and Kreps posit an intuitive explanation according to which the equilibrium introduces a self-reinforcing behaviour that is common knowledge among the players. By giving an emphasis to the equilibrium (outcome) payoffs any deviation from it is perceived as a conscious defection from the outcome. Therefore it needs to be justified on the basis of how it compares to that outcome. This emphasis carries on to our article in terms of choosing the most probable equilibrium outcome.
might have sent, but in equilibrium does not. Such beliefs might upset the given equilibrium. Cho and Kreps posit an intuitive explanation according to which the equilibrium introduces a self-reinforcing behaviour that is common knowledge among the players. By giving an emphasis to the equilibrium (outcome) payoffs any deviation from it is perceived as a conscious defection from the outcome. Therefore it needs to be justified on the basis of how it compares to that outcome. This emphasis carries on to our article in terms of choosing the most probable equilibrium outcome.
We assume that for each state of nature there is one action that has to be selected. To the best of our knowledge, the prevailing assumption in the literature is that if  takes the “correct” action then maximum payoffs will be received by both
takes the “correct” action then maximum payoffs will be received by both  and
and  irrespective of whatever signal
irrespective of whatever signal  has sent. See, for example, [1] , Pawlowitsch [6] , Huttegger [7] . This is a game of common interest in which a resolution leads to optimal payoffs for both actors as noted by Skyrms [8] .
has sent. See, for example, [1] , Pawlowitsch [6] , Huttegger [7] . This is a game of common interest in which a resolution leads to optimal payoffs for both actors as noted by Skyrms [8] .
This type of analysis is not complete on two counts. First, there is little discussion of the case where the action of the receiver may be appropriate (e.g. “correct”) to the state of nature even if the signal sent is not. Second, there is no discussion of what happens to the payoffs of the two agents when this is the case. Lewis, and most recently philosophers like Stokke [9] make an attempt to discuss what constitutes “true” and “untrue” signals by a sender and responses in a signaling system. However there is no discussion of “truthfulness” in relation to “correctness”.
Paper [2] departed from the assumption of a correct decision by the receiver leading to an optimal payoff for both. It distinguished between true signals (by ) and correct actions (by
) and correct actions (by ). Unlike [1] and the majority of the subsequent literature, we noted that a correct action is not always the result of a truthful signal.
). Unlike [1] and the majority of the subsequent literature, we noted that a correct action is not always the result of a truthful signal.  may still correctly guess the state of nature although
may still correctly guess the state of nature although  sends a “wrong” signal. A correct guess by
sends a “wrong” signal. A correct guess by  means that she will receive the maximum payoff.
means that she will receive the maximum payoff.  will not if she has not truthfully revealed a signal that matches the true state of nature. Unlike [1] , in our model a true signal is mutually rewarding if it leads to a correct decision by
will not if she has not truthfully revealed a signal that matches the true state of nature. Unlike [1] , in our model a true signal is mutually rewarding if it leads to a correct decision by 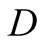 but a correctly guessed state of nature by
but a correctly guessed state of nature by  is not necessarily so. We bind truthfulness (in the report of a signal) to a maximum payoff if accompanied by correctness, but the latter (in terms of the actions of
is not necessarily so. We bind truthfulness (in the report of a signal) to a maximum payoff if accompanied by correctness, but the latter (in terms of the actions of ) is not solely the result of a truthful signal.
) is not solely the result of a truthful signal.  may still correctly guess the state of nature although
may still correctly guess the state of nature although  sends a “wrong” signal i.e. one that deviates from what he has seen. In this case
sends a “wrong” signal i.e. one that deviates from what he has seen. In this case  receives the reward alone but
receives the reward alone but  does not. If
does not. If  ends up doing the incorrect thing then both get zero payoffs.
ends up doing the incorrect thing then both get zero payoffs.
In our current paper of a signaling model with noise,  receives a message that does not necessarily match with the actual true state of nature. Therefore, there is a de-coupling of the truthful revelation of the received information in the form of a signal dispatched by
receives a message that does not necessarily match with the actual true state of nature. Therefore, there is a de-coupling of the truthful revelation of the received information in the form of a signal dispatched by  and whether this signal correctly reflects the state of nature. In other words, the delivery by
and whether this signal correctly reflects the state of nature. In other words, the delivery by  to
to 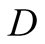 of a signal that does not match the true state of nature does not necessarily imply that the sender has been untruthful in revealing his signal. However, a signal that no longer reflects the true state of nature will imply a zero payoff for
of a signal that does not match the true state of nature does not necessarily imply that the sender has been untruthful in revealing his signal. However, a signal that no longer reflects the true state of nature will imply a zero payoff for . This is irrespective of whether or not it truthfully reflects the private information held by
. This is irrespective of whether or not it truthfully reflects the private information held by  and irrespective of whether
and irrespective of whether ’s actions are correct or not.
’s actions are correct or not.
2. On a Simple Signaling Model with Noise
We introduce the game theoretic analysis by considering a helper/driver example, as in our previous paper [2] . As in the previous model, there are two players, a helper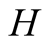 , (he), who tries to direct a driver
, (he), who tries to direct a driver , (she), to park her car. “Nature” selects with probability
, (she), to park her car. “Nature” selects with probability  the state to be either “left” (L) or “right” (R). It is now assumed that player
the state to be either “left” (L) or “right” (R). It is now assumed that player  picks up the correct state of nature with a noise indicated by probability
picks up the correct state of nature with a noise indicated by probability  We have again an imperfect information, non-cooperative signaling game, but this time it is rather more complicated, as the private information of
We have again an imperfect information, non-cooperative signaling game, but this time it is rather more complicated, as the private information of  regarding the state of nature in not precise. We are using again a game theoretic extensive form, dynamic decision tree formulation and the notation for pure and mixed strategies is obvious and that of the previous paper. The vectors of payoffs are given at the terminal nodes of the tree. The first element is the payoff of
regarding the state of nature in not precise. We are using again a game theoretic extensive form, dynamic decision tree formulation and the notation for pure and mixed strategies is obvious and that of the previous paper. The vectors of payoffs are given at the terminal nodes of the tree. The first element is the payoff of  and the second that of
and the second that of .
.
The rules for calculated payoffs are as follows. When  ends up sending the “correct” signal and the correct action, i.e. the one corresponding to the actual state of the world, follows by
ends up sending the “correct” signal and the correct action, i.e. the one corresponding to the actual state of the world, follows by , then both players receive a payoff of 1. If
, then both players receive a payoff of 1. If  communicates an incorrect signal and this leads to an incorrect action by
communicates an incorrect signal and this leads to an incorrect action by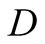 , then both players get 0. If
, then both players get 0. If  sends an incorrect signal and
sends an incorrect signal and  reacts choosing to play in the opposite direction then
reacts choosing to play in the opposite direction then  gets 1 for performing the correct action but
gets 1 for performing the correct action but  ends up with zero.
ends up with zero.
In [2] we made the connection between the resolution of the signaling game without any noise and the ideas of rational expectations (self-fulfilling prophesies) from economic theory, which provide a formal interpretation of the results of our analysis. The expectations of the actors are self-fulfilling and they both receive their optimal payoffs. This connection between the concepts from the neighbouring disciplines of game theory and economics can also be established in the present case in which the existence of noise in the signals makes the game tree formulation more involved.
The structure of the game, the uncertainties introduced, the payoffs and the rationality of the players are common knowledge. Both players,  and
and , make rational decisions taking fully into account all the information which is common knowledge. The implications of their various strategies are clearly laid out. The players make rational predictions, (prophesies), of each others’ actions and on this basis they act themselves. In the rational expectation equilibrium that results the predictions, that is the players’ beliefs, are confirmed. The prophesies of the players are self-fulfilling. We give an explicit example of this below.
, make rational decisions taking fully into account all the information which is common knowledge. The implications of their various strategies are clearly laid out. The players make rational predictions, (prophesies), of each others’ actions and on this basis they act themselves. In the rational expectation equilibrium that results the predictions, that is the players’ beliefs, are confirmed. The prophesies of the players are self-fulfilling. We give an explicit example of this below.
We are concerned with the analysis of the implications of the signals sent by  to
to . The signal of nature and how it is read by the machine are both fixed with given probabilities and this is background information in the analysis. A machine picks up the signal from nature and transmits it to
. The signal of nature and how it is read by the machine are both fixed with given probabilities and this is background information in the analysis. A machine picks up the signal from nature and transmits it to . However, like all machines, it is not a
. However, like all machines, it is not a  accurate. As the signal from nature goes to the machine it can be distorted. This means that if the machine shows on the screen “left”
accurate. As the signal from nature goes to the machine it can be distorted. This means that if the machine shows on the screen “left”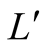 , player
, player  will know that the real state is
will know that the real state is  with probability
with probability  and that with probability
and that with probability  the real state is
the real state is . The situation is analogous if the machine shows on the screen “right”
. The situation is analogous if the machine shows on the screen “right” . That is the machine could have distorted the original signal as it is transmitted on the screen. Player
. That is the machine could have distorted the original signal as it is transmitted on the screen. Player 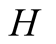 will know that the real state is
will know that the real state is  with probability
with probability , and
, and  with probability
with probability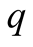 . If the machine is only a bit faulty, we say that
. If the machine is only a bit faulty, we say that  is the noise, due to the “trembling” hand of the machine. The smaller
is the noise, due to the “trembling” hand of the machine. The smaller  is, the more accurate is the transmission. If the machine is very faulty then the possibility of distortion,
is, the more accurate is the transmission. If the machine is very faulty then the possibility of distortion,  , is large and we still call this “noise”, as a technical term. Of course for
, is large and we still call this “noise”, as a technical term. Of course for  we retrieve the previous model.1
we retrieve the previous model.1
The information sets  and
and  of
of  capture the fact that he does not know for sure that what he sees at the screen is a true reflection of the state of nature.
capture the fact that he does not know for sure that what he sees at the screen is a true reflection of the state of nature.  corresponds to seeing
corresponds to seeing  and
and  to observing
to observing . The information sets
. The information sets  and
and  belong to
belong to  and capture the fact that she hears
and capture the fact that she hears  or
or , respectively, but does not know what
, respectively, but does not know what  saw on the screen (e.g.
saw on the screen (e.g.  or
or ). The two players can also play “left” or “right”. In a pair of strategies for
). The two players can also play “left” or “right”. In a pair of strategies for  the first refers to
the first refers to  and the second to
and the second to . In a pair of strategies for
. In a pair of strategies for  the first refers to
the first refers to  and the second to
and the second to . As there is no risk of confusion, and in order to simplify matters, we use the same notation for the left and right moves from the nodes of information sets which belong to the same player.
. As there is no risk of confusion, and in order to simplify matters, we use the same notation for the left and right moves from the nodes of information sets which belong to the same player. 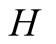 can play
can play  or
or , and
, and  can play
can play  or
or .
.
In a pair of strategies for  the first refers to
the first refers to  and the second to
and the second to . In a pair of strategies for
. In a pair of strategies for  the first refers to
the first refers to  and the second to
and the second to .
.
We refer very briefly to two relevant equilibrium concepts in game theory. A Nash Equilibrium (NE) is a pair of strategies (actions) of the two players which are in terms of payoffs best replies to each other’s.
A behavioural strategy assigns to the information sets of a player independent probability distributions to the actions available from those sets. The equilibrium concept of Perfect Bayesian Equilibrium (PBE) consists of a set of players’ optimal behavioural strategies and consistent with these, a set of beliefs which attach a probability distribution to the nodes of each information set. Consistency requires that the decision from an information set is optimal given the particular player’s beliefs about the nodes of this set and the strategies from all other sets, and that beliefs are formed from updating, using the available information. If the optimal play of the game enters an information set then updating of beliefs must be Bayesian. Otherwise appropriate beliefs are assigned arbitrarily to the nodes of the set. The PBE offers a dynamic interpretation of the solution noncooperative extensive form game. It makes use of the agents beliefs and it is a subset of NE.
The behavioural assumption is that every agent chooses his best strategy given the strategy of the other. That is, in effect, a reaction function is formed. If each player optimizes believing, (prophesyzing), a particular strategy for the other, and the outcome is that there is no reason for anybody to feel they have predicted wrongly, then we have an equilibrium which has been obtained rationally. The confirmation of the predictions takes places where the reaction functions intersect.
In terms of equilibria the distinction is between small , and large
, and large . In Figures 1-5, we have shown the optimal strategies of
. In Figures 1-5, we have shown the optimal strategies of  and
and  with heavy lines.2 The calculations correspond to examples with
with heavy lines.2 The calculations correspond to examples with
 small Figure 1 and Figure 2), large, (Figure 3 and Figure 4) and equal to
small Figure 1 and Figure 2), large, (Figure 3 and Figure 4) and equal to  (Figure 5). The expected payoffs,
(Figure 5). The expected payoffs,  and
and , of the two players are also given. It is straightforward to check that the strategies form a Nash Equilibrium (NE).
, of the two players are also given. It is straightforward to check that the strategies form a Nash Equilibrium (NE).
The calculations, through Bayesian updating, of the conditional probabilities, (beliefs), attached to the nodes of the information sets are based on the strategies and thus we obtain a PBE. The beliefs are shown on the nodes of the information sets. With respect to  and
and  they express the fixed probabilities with respect to which
they express the fixed probabilities with respect to which

Figure 1. q small; E1 = 1 − q, E2 = 1 − q..

Figure 2. An alternative equilibrium with q small; E1 = 0, E2 = 1 − q.

Figure 3. An equilibrium with q large; E1 = 0, E2 = q.

Figure 4. An alternative equilibrium with q large; E1 = q, E2 = q.

Figure 5. An equilibrium with q =1/2; E1 = 0, E2 =1/2.
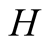 believes that a signal is true of false.3
believes that a signal is true of false.3
In the end, we are interested in the players taking, from their information sets, decisions with probability one. In particular we want to analyse the case when  will instruct
will instruct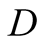 , with probability 1, to turn “left” or “right” and
, with probability 1, to turn “left” or “right” and  will also play a pure strategy. Eventually we want to know which combination of pure strategies is most likely to prevail, i.e. whether the signal of
will also play a pure strategy. Eventually we want to know which combination of pure strategies is most likely to prevail, i.e. whether the signal of  will be truthful and if
will be truthful and if  will believe it.
will believe it.
Case 1.  is small. The optimal paths are shown in Figure 1. The information set
is small. The optimal paths are shown in Figure 1. The information set  contains the nodes, from left to right,
contains the nodes, from left to right,  , and we wish to calculate the beliefs attached to these by
, and we wish to calculate the beliefs attached to these by  Using the Bayesian formula for updating beliefs, (see for example Glycopantis, Muir and Yannelis [10] ), we can calculate these conditional probabilities. We know that
Using the Bayesian formula for updating beliefs, (see for example Glycopantis, Muir and Yannelis [10] ), we can calculate these conditional probabilities. We know that  is entered only if
is entered only if  plays
plays . Hence
. Hence

Similarly we obtain the conditional probabilities 
 and
and .
.
On the other hand  is entered only if
is entered only if  plays
plays  The information set
The information set  contains the nodes, from left to right,
contains the nodes, from left to right,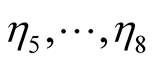 . We now have
. We now have
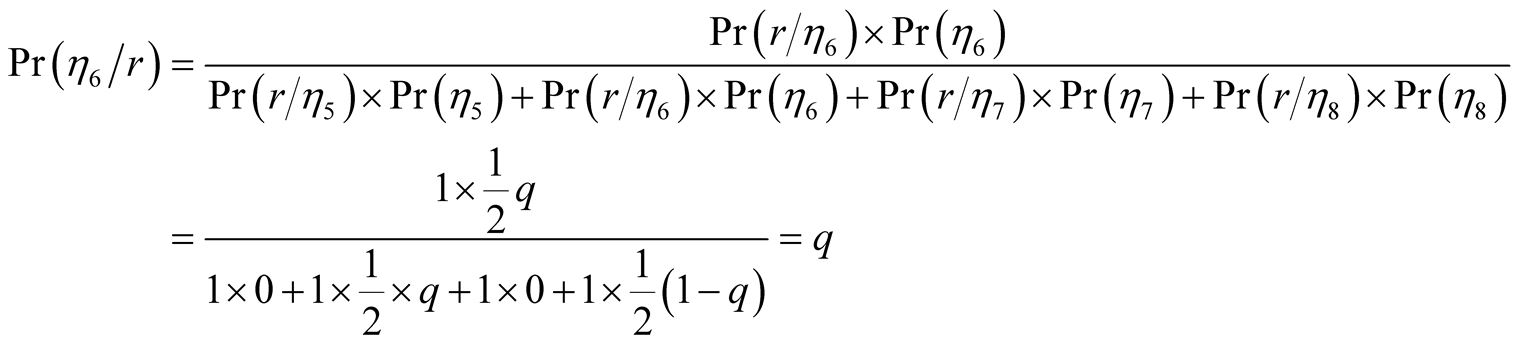
Similarly we obtain the conditional probabilities 
 and
and .
.
Given  small, player
small, player  will follow in his action the state that he observes almost surely, expecting that
will follow in his action the state that he observes almost surely, expecting that  will realize this, and thus turn herself in the same direction. Essentially,
will realize this, and thus turn herself in the same direction. Essentially,  is punished if he fails to report the signal that he has seen on the screen. The noise it contains, means that despite the truthful revelation, it is not always a correct reflection of the true state of nature and hence the expected payoffs reflect this by being less than 1.
is punished if he fails to report the signal that he has seen on the screen. The noise it contains, means that despite the truthful revelation, it is not always a correct reflection of the true state of nature and hence the expected payoffs reflect this by being less than 1.
In terms of Figure 1, the prophesies which form a rational expectations equilibrium take the following form.  prophesizes that when
prophesizes that when  hears
hears  she will believe that
she will believe that  has observed
has observed  and therefore she will play
and therefore she will play  because she knows that if she takes the correct decision she will get an optimum payoff.
because she knows that if she takes the correct decision she will get an optimum payoff.  prophezises that when
prophezises that when  sees
sees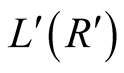 , given that the noise is small, he will repeat the message sent by the machine and play
, given that the noise is small, he will repeat the message sent by the machine and play  since if he transmits a correct signal he may get an optimum payoff, whereas if he transmits a signal that does not reflect the state of nature he will not irrespective of what
since if he transmits a correct signal he may get an optimum payoff, whereas if he transmits a signal that does not reflect the state of nature he will not irrespective of what  plays.
plays.
We shall now discuss how these rational decisions of the agents are locked in a fixed point. As optimal reactions to each other’s actions they confirm themselves.
The fixed point equilibrium is characterized as follows.  plays from
plays from  the choices
the choices  and
and  with probabilities
with probabilities  and
and  respectively, and from
respectively, and from  the choices
the choices  and
and 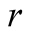 with probabilities
with probabilities  and
and  respectively.
respectively.  plays from
plays from 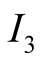 the choices
the choices 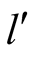 and
and  with probabilities
with probabilities  and
and  respectively, and
respectively, and  the choices
the choices 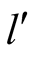 and
and  with probabilities
with probabilities  and
and  respectively.
respectively.
If  chooses
chooses  and
and  then the resulting expected payoff for
then the resulting expected payoff for , ignoring
, ignoring , is
, is

which is maximized at  and
and . On the other hand for
. On the other hand for  and
and , we obtain
, we obtain

which, given that q is small, is maximized at  and
and  Hence the the pairs
Hence the the pairs 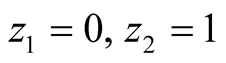 and
and  confirm each other as a fixed pair. Starting from one pair of rational decisions we go back and confirm it.
confirm each other as a fixed pair. Starting from one pair of rational decisions we go back and confirm it.
In terms of reaction functions the Kakutani fixed point theorem is seen as follows. Let ,
,  be the two vectors and
be the two vectors and ,
,  the reaction functions (correspondences) of the helper and the driver respectively. The fixed point satisfies
the reaction functions (correspondences) of the helper and the driver respectively. The fixed point satisfies .
.
We have analyzed the equilibrium . Inserting back in our calculations the fraction
. Inserting back in our calculations the fraction , the resulting payoffs are
, the resulting payoffs are  and
and .
.
The pair  and
and  are the best possible payoffs and hence the best candidates for optimality because each time
are the best possible payoffs and hence the best candidates for optimality because each time  follows the message of the machine, i.e. he reports correctly, he is right with a high probability and
follows the message of the machine, i.e. he reports correctly, he is right with a high probability and 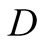 follows his suggestion. So with a high probability,
follows his suggestion. So with a high probability,  , both players get each time payoff 1. In expectation they get each time
, both players get each time payoff 1. In expectation they get each time  and there are two such times. We discuss this further below.
and there are two such times. We discuss this further below.
We can provide some further explanation with respect to the expected payoffs. A folded up tree can be obtained through backward induction. We are using the optimal strategies of  given that
given that . In the folded up tree of Figure 1 it is clear the
. In the folded up tree of Figure 1 it is clear the  must use
must use  from point
from point  and
and 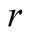 from 2.
from 2.
Now, the PBE is a technical definition and as such it allows for other such equilibria as well. For example the following pairs of behavioural strategies ,
,  , and
, and  form a PBE.
form a PBE.
In Figure 2 we consider, in particular, the strategies  which also form a PBE, but with payoff lower for
which also form a PBE, but with payoff lower for  than that corresponding to the pair
than that corresponding to the pair .
.
We shall now discuss also for the pair  how these rational decisions of the agents form a fixed point and thus confirm themselves.
how these rational decisions of the agents form a fixed point and thus confirm themselves.
The fixed point equilibrium is found as follows. Again 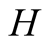 plays from
plays from  the choices
the choices  and
and  with probabilities
with probabilities  and
and  respectively, and from
respectively, and from  the choices
the choices  and
and  with probabilities
with probabilities  and
and  respectively.
respectively.  plays from
plays from  the choices
the choices  and
and 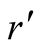 with probabilities
with probabilities 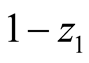 and
and  respectively, and
respectively, and  the choices
the choices 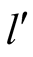 and
and  with probabilities
with probabilities  and
and  respectively.
respectively.
The mathematical analysis is supported by optimal decisions obtained by analyzing the graph. From Figure 2 we obtain the optimal decisions ,
,  ,
,  and
and 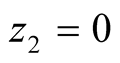 If
If  chooses
chooses  and
and  then the resulting expected payoff for
then the resulting expected payoff for  is seen to be
is seen to be  irrespective of
irrespective of  and
and . Therefore this value is also obtained
. Therefore this value is also obtained ,
, . On the other hand for
. On the other hand for ,
,  , we obtain, ignoring
, we obtain, ignoring ,
,

which is maximized at  and
and  Hence the the pairs
Hence the the pairs  and
and  confirm each other as a fixed pair. Starting from one pair of rational decisions we go back and confirm it.
confirm each other as a fixed pair. Starting from one pair of rational decisions we go back and confirm it.
We have analyzed the equilibrium . Inserting back in our calculations the fraction
. Inserting back in our calculations the fraction , the resulting payoffs are
, the resulting payoffs are  and
and . In Figure 2 the beliefs of player
. In Figure 2 the beliefs of player 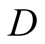 are given for both the points in the information set
are given for both the points in the information set  and those in
and those in . These are consistent with the moves up to these points and guarantee the optimality of the moves which follow.
. These are consistent with the moves up to these points and guarantee the optimality of the moves which follow.
We return now to the issue of the most likely equilibrium to prevail. From the four pure NE referred to above, it is easy to see that in the case of  and
and  the signal of
the signal of  has zero informational content. Hence the “updated” beliefs of
has zero informational content. Hence the “updated” beliefs of  in
in  and
and  are identical to the priors of the alternative states of nature.
are identical to the priors of the alternative states of nature.
This leads to equilibrium expected payoffs of . Regarding
. Regarding , we see that the expected payoff for
, we see that the expected payoff for  is zero. In other words, the sender will be punished for being untruthful in terms of revealing his private information regarding the state of nature as seen on the machine, as the probability that this is wrong is small. Hence if
is zero. In other words, the sender will be punished for being untruthful in terms of revealing his private information regarding the state of nature as seen on the machine, as the probability that this is wrong is small. Hence if 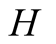 misreports what he has seen on the machine, then he is likely to have send an incorrect signal regarding the state of nature. He will be punished for this with a zero payoff. Given this, player
misreports what he has seen on the machine, then he is likely to have send an incorrect signal regarding the state of nature. He will be punished for this with a zero payoff. Given this, player  can reasonably expect that
can reasonably expect that  has an interest to report truthfully what he has seen on the machine.
has an interest to report truthfully what he has seen on the machine.
In cheap talk games speech serves the purpose of reinforcing a particular action and provides the evolutionary process rationale for choosing a particular equilibrium. Similarly, in a signaling game,  will believe that the sender will send him true information unless he has a reason to deceive him. Using the idea of rational expectations it is obvious that
will believe that the sender will send him true information unless he has a reason to deceive him. Using the idea of rational expectations it is obvious that  has an interest to report the truth regarding his private information because failing to do so hurts him. Hence
has an interest to report the truth regarding his private information because failing to do so hurts him. Hence  can reasonably expect and correctly guess that he will signal truthfully. This leads to the formation of a language (signaling) convention between the players.
can reasonably expect and correctly guess that he will signal truthfully. This leads to the formation of a language (signaling) convention between the players.
Therefore, given  small, the equilibrium
small, the equilibrium  in Figure 1 is the most likely to prevail, as it involves the maximum possible payoff for both
in Figure 1 is the most likely to prevail, as it involves the maximum possible payoff for both  and
and  and hence is the best candidate for optimality in a repeated game of trial and error until a signaling convention is achieved.
and hence is the best candidate for optimality in a repeated game of trial and error until a signaling convention is achieved.
Finally, we also consider a case of a pair of strategies which do not form a NE. As it is easy to see this is the case if in Figure 1 where all decisions are kept the same apart from changing for the driver  to
to  in
in  i.e. the pair of strategies are
i.e. the pair of strategies are . In this case
. In this case  can change from
can change from  in
in  to
to  and improve her payoff.
and improve her payoff.
Case 2.  is large. The optimal paths are shown in Figure 3 and Figure 4. It is easy to check that the heavy lines strategies form a NE. In Figure 3 only the strategies of
is large. The optimal paths are shown in Figure 3 and Figure 4. It is easy to check that the heavy lines strategies form a NE. In Figure 3 only the strategies of 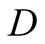 are different. On the other hand, since the optimal actions of
are different. On the other hand, since the optimal actions of  are the same for both small and large
are the same for both small and large  we shall be obtaining, through the Bayesian updating of conditional probabilities, the same beliefs for the nodes of
we shall be obtaining, through the Bayesian updating of conditional probabilities, the same beliefs for the nodes of  and
and  as in Figure 1. In the case of the equilibrium in Figure 3,
as in Figure 1. In the case of the equilibrium in Figure 3,  does not take into account the fact that the machine is so faulty that it is more often wrong than right and he gets punished for truthfully sending what is likely to be an incorrect signal. Player
does not take into account the fact that the machine is so faulty that it is more often wrong than right and he gets punished for truthfully sending what is likely to be an incorrect signal. Player  does not believe the signal she received, turns in the correct direction and she is rewarded. As a result
does not believe the signal she received, turns in the correct direction and she is rewarded. As a result 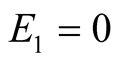 and
and .
.
In Figure 4 we show an alternative NE for large 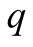 and corresponding beliefs at the nodes of the information sets
and corresponding beliefs at the nodes of the information sets  and
and  and hence an alternative PBE to that in Figure 3. In this case both players make the correct move and they are both rewarded. Specifically,
and hence an alternative PBE to that in Figure 3. In this case both players make the correct move and they are both rewarded. Specifically,  reports the opposite of what he sees, and both him and
reports the opposite of what he sees, and both him and  end up with payoffs
end up with payoffs 
The pair  and
and 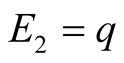 are the best possible payoffs and hence the best candidates for optimality. The machine is now very faulty and each time
are the best possible payoffs and hence the best candidates for optimality. The machine is now very faulty and each time  makes a guess he does not follow its message, i.e. he misreports, and he is right with a high probability and
makes a guess he does not follow its message, i.e. he misreports, and he is right with a high probability and  follows his suggestion. So with a high probability, q, both players get each time payoff 1. In expectation they get each time
follows his suggestion. So with a high probability, q, both players get each time payoff 1. In expectation they get each time  and there are two such times.
and there are two such times.
Again for completeness, we also consider a case of a pair of strategies which do not form a NE. This is the case, as it is easy to see, if in Figure 3 all decisions are kept the same apart from changing for the driver  to
to  in
in .
.
Finally we note that it is easy to see that in both Figure 3 and Figure 4 the actions of the optimal paths satisfy Kakutani’s fixed point theorem and form a rational expectation equilibrium.
Case 3.  We can now have an equilibrium such that only information set
We can now have an equilibrium such that only information set  or only
or only , as shown in
, as shown in
Figure 5, is visited. Suppose that the latter is the case. With respect to the arbitrary beliefs for  which is not visited by the optimal strategies, we can adopt beliefs such that the optimal choice is
which is not visited by the optimal strategies, we can adopt beliefs such that the optimal choice is .
.
Coming now to , all its nodes are visited as player
, all its nodes are visited as player  plays constantly
plays constantly . The beliefs through Bayesian updating are as follows.
. The beliefs through Bayesian updating are as follows.

Similarly we obtain the conditional probabilities 
 and
and
 .
.
We now have that 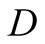 plays
plays  from
from 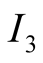 and
and  from
from , while
, while  always plays
always plays  We want to check that
We want to check that  is a NE. Given the strategies of one player we have to consider the alternative actions of the other. Given constant
is a NE. Given the strategies of one player we have to consider the alternative actions of the other. Given constant , player
, player  has made an optimal choice. For the response of
has made an optimal choice. For the response of  to
to  of
of , it is straightforward, inspecting the graph, that
, it is straightforward, inspecting the graph, that  cannot change a strategy and improve his payoff. Hence
cannot change a strategy and improve his payoff. Hence
 forms a NE. The payoffs are
forms a NE. The payoffs are  and
and  Player
Player  is punished if D decides to play
is punished if D decides to play 
in .
.
We shall now discuss how these rational decisions of the agents are locked in a fixed point. As optimal reactions to each other’s actions they confirm themselves and the form a rational expectations equilibrium.
Suppose we consider  and
and . These values mean that
. These values mean that  irrespective of
irrespective of  and
and , and therefore we can choose
, and therefore we can choose 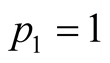 and
and  which
which  takes as given and calculates, ignoring
takes as given and calculates, ignoring ,
,

which means that  irrespective of
irrespective of  and
and  and therefore we can choose
and therefore we can choose , and
, and 
In fact, we have a multiplicity of equilibria as D could play instead . The pairs of strategies
. The pairs of strategies  and
and  form also equilibria. In each of these case the beliefs at the nodes of the information sets of
form also equilibria. In each of these case the beliefs at the nodes of the information sets of  are properly adjusted, but the payoffs of
are properly adjusted, but the payoffs of  and
and  are the same. That is
are the same. That is  and
and . A general argument can be advanced that the pair
. A general argument can be advanced that the pair  are the best possible payoffs and hence the best candidates for equilibrium.
are the best possible payoffs and hence the best candidates for equilibrium.
The machine is now faulty with probability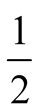 . Each time
. Each time  makes a guess he has an equal chance to report or misreport the correct state of nature and when
makes a guess he has an equal chance to report or misreport the correct state of nature and when  responds she has an equal chance of discovering the true state of nature.
responds she has an equal chance of discovering the true state of nature.
Now, with respect to , since she is rewarded for guessing correctly, she will always get expected payoff
, since she is rewarded for guessing correctly, she will always get expected payoff
 However the reward of
However the reward of  is calculated, as explained above, in a more complicated manner. He will only get a payoff of 1 if his signal coincides with the correct choice of
is calculated, as explained above, in a more complicated manner. He will only get a payoff of 1 if his signal coincides with the correct choice of ; otherwise he gets
; otherwise he gets  It is therefore possible that
It is therefore possible that  gets payoff 0 because he has signaled the opposite of the action taken by
gets payoff 0 because he has signaled the opposite of the action taken by . On the other hand the latter by making a constant choice secures for himself payoff
. On the other hand the latter by making a constant choice secures for himself payoff 
Finally, we state a pair of strategies which do not form a NE. This is the case, as it is straightforward to see, of the pair . If
. If  chooses
chooses  then
then  can improve his payoff by switching to
can improve his payoff by switching to .
.
3. Further Discussion and Conclusions
We have analysed a sequential game concerning instructions and decisions to and by players, where nature selects a state and a machine transmits a noisy signal which is received by a helper,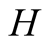 . The latter decides whether to truthfully report this signal to a driver,
. The latter decides whether to truthfully report this signal to a driver, . For a small noise the equilibrium outcome, not the payoffs, is the same as in the case
. For a small noise the equilibrium outcome, not the payoffs, is the same as in the case  discussed in the earlier paper, but for a large noise
discussed in the earlier paper, but for a large noise  will be punished for truthfully sending to
will be punished for truthfully sending to  a false message.
a false message.
With respect to payoffs, both players know that if the noise in the signal is small, announcements by  which are not reflective of the state of nature will lead to outcomes that will hurt them. The incentives of
which are not reflective of the state of nature will lead to outcomes that will hurt them. The incentives of  and
and  are compatible in the sense that
are compatible in the sense that 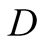 can reasonably expect and correctly guesses that
can reasonably expect and correctly guesses that  has an incentive to truthfully report a signal, when that signal is likely to be a correct reflection of the state of nature.
has an incentive to truthfully report a signal, when that signal is likely to be a correct reflection of the state of nature.
In the case of a noisy signal  may receive an incorrect signal from the machine which he reports truthfully. Even if the final choice is correct, his expected payoff will in this case be zero. So truthfulness no longer automatically implies that a correct signal is sent.
may receive an incorrect signal from the machine which he reports truthfully. Even if the final choice is correct, his expected payoff will in this case be zero. So truthfulness no longer automatically implies that a correct signal is sent.
As argued in [2] , the assumption of an aligned interest between the helper, as the sender of a signal, and the driver as the receiver is found in much of the existing literature. The incentive of  to choose
to choose  rather than
rather than  no longer applies if
no longer applies if ’s payoff is no longer dependent on being correct. This would make the helper careless in terms of his reporting. He knows that his payoff is dependent on the final outcome which is determined by the actions of the driver irrespective of whether his signal reflects the true state of nature. The result of this assumption is that the formation of a convention is made less likely. This will still hold true in the case of a noisy signal, as long as
’s payoff is no longer dependent on being correct. This would make the helper careless in terms of his reporting. He knows that his payoff is dependent on the final outcome which is determined by the actions of the driver irrespective of whether his signal reflects the true state of nature. The result of this assumption is that the formation of a convention is made less likely. This will still hold true in the case of a noisy signal, as long as .
.
In contrast, in our model,  knows that the probability of his signal to
knows that the probability of his signal to  correctly reflecting the state of nature is more likely if he truthfully reports to
correctly reflecting the state of nature is more likely if he truthfully reports to  the signal he has received from the machine. Since being correct is a necessary condition for his getting a strictly positive payoff, the case is identical to the one discussed in [2] where
the signal he has received from the machine. Since being correct is a necessary condition for his getting a strictly positive payoff, the case is identical to the one discussed in [2] where .
.
In the case of a large , the incentive of
, the incentive of  to report a signal that correctly reflects the state of nature still applies. But in this case, it means that
to report a signal that correctly reflects the state of nature still applies. But in this case, it means that  has an incentive to report the opposite of what has been transmitted to him by the machine. In other words, it is not in the interests of
has an incentive to report the opposite of what has been transmitted to him by the machine. In other words, it is not in the interests of  to truthfully report the message he has received by the machine (private information). By reporting exactly the opposite of what he sees,
to truthfully report the message he has received by the machine (private information). By reporting exactly the opposite of what he sees,  is more often correct than not. Hence in this case there is an inverse relationship between correctness and truthfulness.
is more often correct than not. Hence in this case there is an inverse relationship between correctness and truthfulness.
In both Case 1 and Case 2 we get a number of different PBE. Only one of these seems to be justified in providing an equilibrium which introduces a self enforcing behaviour and also provides an optimum outcome for both players.
In Case 3 there is also a number of equilibria. However from these only two PBE secure an optimum payoff for both players. These are the ones where both  and
and  make constant choices from both of their corresponding information sets. However unlike the PBE in Cases 1 and 2, these optimal payoffs do not exceed the default payoff of
make constant choices from both of their corresponding information sets. However unlike the PBE in Cases 1 and 2, these optimal payoffs do not exceed the default payoff of  choosing an action randomly (i.e.
choosing an action randomly (i.e. ) as the informational value of the signals by
) as the informational value of the signals by 
is zero.
Acknowledgements
We wish to thank Professor Dimitrios Tsomokos of Oxford University for his suggestions and penetrating comments which led to a substantial improvement of the final draft. Of course responsibility for all short comings stays with the authors.
NOTES
1The beginning of the idea of H receiving a false message from the machine regarding the state of nature was very briefly mentioned in , p. 5.
2We could interpret “Nature” and the “Machine” as two (passive) players, receiving, each, payoff zero, and playing the indicated mixed strategies.

3In order to simplify the graphs, only in Figure 1 we have inserted explicitly that the actions of the players from the information sets can be mixed with probabilities as follows:  from
from ,
,  from
from ,
,  from
from  and
and  from
from . Exactly the same notation is assumed in all the graphs. Also, only in Figure 1 we insert the folded up tree following the optimal decisions of
. Exactly the same notation is assumed in all the graphs. Also, only in Figure 1 we insert the folded up tree following the optimal decisions of . Corresponding folded up trees can be obtained for all other figures displayed.
. Corresponding folded up trees can be obtained for all other figures displayed.