Lecture Notes of Möbuis Transformation in Hyperbolic Plane

Rania B. M. Amer

Department of Engineering Mathematics and Physics, Faculty of Engineering, Zagazig University, Zagazig, Egypt.

DOI: 10.4236/am.2014.515215                

Abstract

In this paper, I have provided a brief introduction on M?bius transformation and explored some basic properties of this kind of transformation. For instance, M?bius transformation is classified according to the invariant points. Moreover, we can see that M?bius transformation is hyperbolic isometries that form a group action PSL (2, R) on the upper half plane model.

Keywords

The Upper Half-Plane Model, Möbius Transformation, Hyperbolic Distance, Fixed Points, The Group PSL (2, R)

1. Introduction

Möbius transformations have applications to problems in physics, engineering and mathematics. Furthermore, the conformal mapping is represented as bilinear translation, linear fractional transformation and Mobius transformation.

Möbius transformations are also called homographic transformations, linear fractional transformations, or fractional linear transformations and it is a bijective holomorphic function (conformal map) [1] [2] .

The purpose of this paper is studied the properties of Möbius transformations in detail, and some definitions and theorems are given. The basic properties of these transformations are introduced and classified according to the invariant points. Möbius transformations are formed a group action PSL (2,Â) on the upper half plane model.

A Möbius transformation of the plane is a map f: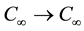

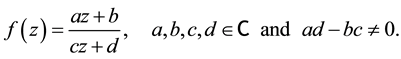(1-1)

which sending each point to a corresponding point, where z is the complex variable and the coefficients a, b, c, d are complex numbers [3] .

Definition (1-1).

The upper half plane model is defined by the set

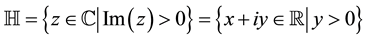(1-2)

and the boundary of is defined by

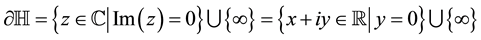(1-3)

The lines (geodesics) are vertical rays and semicircles orthogonal to ¶H. The angles are Euclidean angles.

Definition (1-2).

A Möbius transformations form a group which is denoted by.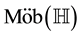

Remark (1-3).

Since Möbius transformation takes the form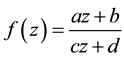

If the point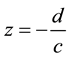, this means 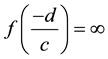so 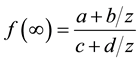and we get the following:

1)

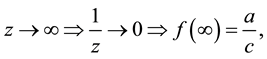
2) If c = 0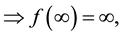

3) If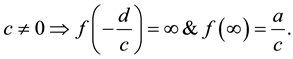

Lemma (1-4).

A Möbius transformation consists of four composition functions.

Proof.

The four functions are:

1) translation by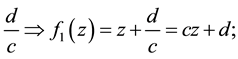

2) inversion and reflection with respect to real axis 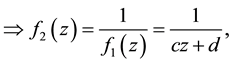then the plane inside turn out and the lines on the plane are lines or circles and right angles stay true and also the circles are circles;

3) dilation and rotation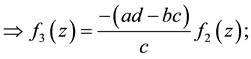

4) translation by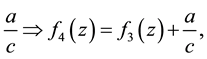

(1-4)

Remark (1-5).

We can write Möbius transformations as follows

(1-5)

The inverse Möbius transformation is evaluated from the inverse of the metric

then

(1-6)

Theorem (1-6).

Möbius transformations also preserve cross ratio.

Proof.

Given four distinct points z₁, z₂, z₃, z₄, their cross ratio is defined by

(1-7)

The cross ratio is invariant of the group of all Möbius transformation so if we transform the four points z_i into by an inversion, the cross ratio of these points are taken into its conjugate value, and the cross ratio is invariant under a product of two or any even number of inversions and exchanging any two pairs of coordinates preserves the cross-ratio. Then

(1-8)

Since translation, rotation and dilation preserve cross ratio and Möbius transformation consists of them so Möbius transformation preserves cross ratio.

Corollary (1-7).

(1-9)

If, we get

(1-10)

and therefore

(1-11)

If any one of z_i = 0 for example z₃ = 0, then

(1-12)

Since the trace of matrix A is tr(A) = a + b and this trace is invariant under conjugation, this is mean,

. (1-13)

Every Möbius transformation can be represented by normalized matrix A such that its determinant equal one which mean ad − bc = 1.

Lemma (1-8).

Two Möbius transformations A, B with are conjugate if and only if

. (1-14)

Poof.

Let

Since matrix A and B are Möbius transformations, then

Since, then

If and only if then matrix A and matrix B must be conjugate.

2. The Fixed Points in Mobius Transformation

A Möbius transformation is

Since fixed points (i.e. invariant points) is defined by f(z) = z, then

This mean, then the fixed points are given by

(1-15)

For non parabolic transformation, there are two fixed points 0, ¥ but for parabolic transformation, there is only fixed points ¥ because the fixed points are coincide.

3. The Types of Mobius Transformations

There are Parabolic, elliptic, hyperbolic and loxodromic which are distinguished by looking at the trace tr(A) = a + b.

3.1. For Parabolic Transformations

tr²(A) = 4, the parabolic Möbius transformations forms subgroup isomorphic to the group of matrices [4] ,

, (1-16)

which describes a translation and this transformation is orientation preserving.

3.2. For Hyperbolic Transformations

, the hyperbolic Möbius transformations forms subgroup isomorphic to the group of matrices

, (1-17)

which describes a rotation and this transformation is orientation preserving.

3.3. For Elliptic Transformations

, the elliptic Möbius transformations forms subgroup isomorphic to the group of matrices

, (1-18)

which describes a rotation and this transformation is orientation preserving.

3.4. For Loxodromic Transformations

, the Loxodromic Möbius transformations forms subgroup isomorphic to the group of matrices,

, (1-19)

which describes a dilation (homothety) and this transformation is orientation preserving.

The difference between orientation preserving (invariant) and orientation reversing:

1) Rotation and translation are orientation-preserving.

2) Reflection and glide-reflection are orientation-reversing.

3) A composition of orientation-preserving functions is orientation-preserving.

4) A composition of two orientation-reversing functions is orientation-preserving.

5) A composition of one orientation-preserving function and one orientation-reversing function is orientation- reversing.

6) The determinant of the matrix A = 1 (which mentioned above) then the orientation-preserving but if the determinant of the matrix A = ‒1 then the orientation reversing

7) such that is orientation-preserving but with is orientation-reversing, where which mean the point z in the imaginary axis.

8) In Orientation preserving all non collinear points A, B, C, the proper angle measures of the angles ABC and A'B'C' have the same sign but in orientation reversing all non collinear points A, B, C, the proper angle measures of the angles ABC and A'B'C' have opposite signs.

9) Orientation preserving isometries takes counterclockwise angles to counterclockwise angles, and it takes clockwise angles to clockwise angles. An orientation reversing isometries takes counterclockwise angles to clockwise angles, and it takes clockwise angles to counterclockwise angles.

4. Isometries in Mobius Transformation

Definition (4-1).

The group [4] is the projective special linear group of dimension 2 over the real numbers and the determinant of the elements of that group may be 1 or −1 so and this group act on

by Möbius transformations and also the matrices of this group conjugate to the matrix such

that from the Jordan and normal form of a real 2 by 2 matrix and therefore the determinants of these matrices must equal 1, we can see that the absolute value of the traces of the matrices will be respectively less than 2, called elliptic, greater than 2, called hyperbolic, and equal to 2, called parabolic.

Definition (4-2).

Let be path so the hyperbolic distance between two points (a, b) on the upper half plane

with metric is defined by which can be written as

(1-20)

Remark (4-3).

From this definition the geodesic between two points (x₀, y₁) and (x₀, y₂) on the vertical line with y₂ > y₁ has length ln(y₂/y₁) but if two points do not lie on a vertical line so the geodesics is circular arc with center on the x-axis as seen in Figure 1.

Remark (4-4).

From the definition (1-1) we can define the isometry of hyperbolic plane as follows:

Let a mapping f: and let A and B two points in, the mapping f is an isometry if the hyperbolic distance.

Theorem (4-4).

Möbius transformations act isometries in this mean acts isometry on upper half plane by Möbius transformations.

Proof.

Möbius transformations preserve distance. A bijective map that preserves distance is called an isometry because an isometry is a transformation which preserves distance. Thus Möbius transformations are isometries of H.

A second proof.

Since the form of Möbius transformations are, differentiate this form yields to .

Since

Then

(1-21)

From this equation we remark that Möbius transformations preserve the hyperbolic metric so that Möbius transformations are hyperbolic isometries.

A third proof.

From the definition of hyperbolic distance, we want to show that.

Since so the hyperbolic metric is defined by, since the right hand side

Figure 1. The plane as boundary of half space model of hyperbolic space.

(1-22)

Let, then

(1-23)

and from, then

(1-24)

Since the left hand side is

(1-25)

Since and so

Then

(1-26)

We get the left hand side equal the right hand side, and then the proof is complete.

Lemma (4-5).

Let Mobius transformations, then

. (1-27)

Proof.

The right hand side And therefore the left hand side.

We get the left hand side equal the right hand side, and then the proof is complete.

Remark (4-6).

The group acts on by Mobius transformation

(1-28)

This action is faithful and isomorphic to the group of all orientation preserving isometrics of and act discontinuously on so we can write. This mean which preserve the hyperbolic geometry of and therefore the elements in Möbius transformation act by isometries in [5] .

Theorem (4-7).

All orientation-preserving isometries of are Mobius transformations, and all orientation-reversing isometries of are the composition of a Mobius transformation and reflection through the imaginary axis.

Proof.

The isometry group of hyperbolic plane is denoted by which identified with the group of Mobius transformations, and the group of orientation preserving isometries which is the distance preserving maps are the Mobius transformations which preserve and is denoted by which identified with such that acts on the boundary of the upper half plane by

(1-29)

and then, we get:

(1-30)

Let f(z) is an isometry of, and by applying the transformations (rotation) z → kz and inversion z → −1/z, we assume that

(1-31)

Let z₁, z₂ be two points lie in positive imaginary axis. Let the point z not lie in positive imaginary axis and draw two hyperbolic circles with center z₁ and z₂ and passing through z, we find these circles intersect in z, and these circles are mapped into themselves under the isometry so or z.

The first case:

If, we get such that, which is the orientation re-

serving isometries is given by the map, that is the reflection in the imaginary axis and by composition this with Möbius transformations. This means all orientation-reversing isometries of are the composition of a Mobius transformation and reflection through the imaginary axis such that the reflections are isometries that have infinitely many fixed lie on the mirror line.

The second case:

If, we get such that, which is the orientation pre-

serving isometries is given by the rotation z → kz and inversion z →−1/z. This means all orientation-preserving isometry of are Mobius transformations and as we know Mobius transformations consist of a rotation inversion and a translation.

Theorem (4-8).

Möbius transformations preserve circles and lines (Figure 2).

Proof.

Let the transformation w = 1/z is an inversion and every Möbius transformation (Figure 3) f(z) of the form (1.1) is a composition of finitely many similarities and inversions [6] -[9] .

Since w = u + iv and z = x + iy, then

Figure 2. Circle-preserving maps from the plane to itself.

Figure 3. Möbius transformation is composition of multiple inversions.

(1-32)

From the equation of the circle

(1-33)

But if A = 0, it is a line, if, it is a circle.

We can write again the Equation (1-33) w.r.t u, v as follows, which is the equation of a circle.

If D = 0, it is a line, if, it is a circle.

So Möbius transformations preserve circles and lines.

Remark (4-9).

From the last theorem (1-5), we find that the circle goes through the origin may be mapped to the circle or the line.

Theorem (4-10).

Möbius transformations preserve distance.

Proof.

From theorem (1-2) Möbius transformations act isometries in and from definition of isometries we get that the distance between any two points in the hyperbolic plane is invariant by Möbius transformations and Möbius transformations preserve circles (from translation and inversion) and angles so Möbius transformations preserve distance.

5. Conclusion

The properties of Möbius transformations are introduced in detail, and some definitions and theorems are given to show that Möbius transformations are one-to-one, onto and conformal mapping. Also, Möbius transformations map circles to circles and also, map the real line to the real line such that the coefficients a, b, c and d are real. Every orientation-preserving isometrics of the hyperbolic plane is Möbius transformations. Every orientation-reversing isometrics of the hyperbolic plane is a composition of Möbius transformations and reflection. is a group under composition and Möbius transformations map the upper half-plane to itself bijectively. So Möbius transformation maps vertical straight lines in and circles in with real centers to vertical straight lines and circles with real centers. Furthermore, the connections between Möbius transformations, isometries of the hyperbolic plane, and PSL(2; R) are presented.

Acknowledgements

I wish to express my gratitude towards to Professor Dr. William M. Goldman, University of Maryland and Distinguished Scholar-Teacher Professor, Department of Mathematics, for his valuable, guidance, patience and support. I consider myself very fortunate for being able to work with a very considerate and encouraging professor like him.

Conflicts of Interest

The authors declare no conflicts of interest.

References

[1]	Yilmaz, N. (2009) On Some Mapping Properties of Möbius Transformations. The Australian Journal of Mathematical Analysis and Applications, 6, 1-8.
[2]	Nehari, Z. (1952) Conformal Mapping. McGraw-Hill Book, New York.
[3]	John, O. (2010) The Geometry of Möbius Transformations. University of Rochester, Rochester.
[4]	Graeme, K.O. (2012) Random Discrete Groups in the Space of Möbuis Transformations. Msc Thesis, Massey University, Albany.
[5]	Aramayona, J. (2011) Hyperbolic Structures on Surfaces. Lecture Notes Series, IMS, NUS, 9.
[6]	Beardon, A.F. (1995) The Geometry of Discrete Groups, Graduate Texts in Mathematics, 91. Springer-Verlag, New York.
[7]	Jones, G.A. and Singerman, D. (1987) Complex Functions, an Algebraic and Geometric Viewpoint. Cambridge University Press, Cambridge. http://dx.doi.org/10.1017/CBO9781139171915
[8]	Lehner, J. (1964) Discontinuous Groups and Automorphic Functions, Mathematical Surveys, 8. American Mathematical Society, Providence. http://dx.doi.org/10.1090/surv/008
[9]	Seppälä, M. and Sorvali, T. (1992) Geometry of Riemann Surfaces and Teichmüller Spaces, Chapter 1. Elsevier Science Publishing Company, INC, New York, 11-58.