Distribution of Solar Irradiance on Inclined Surfaces Due to the Plane of the Ground ()
1. Introduction
In order to achieve the nearly zero energy building (nZEB) requirements by 2021, energy efficient façades are one important factor in the design of such buildings [1] . Passive architectural cooling and heating have a strong impact on the heating, cooling and electric lighting energy needs, as well as on daylight.
A self-shading façade that is an inclined surface, due to the plane of the ground, is one option among passive cooling strategies. Figure 1 and Figure 2 show such buildings in Tallinn, Estonia. The role of alternative passive design principals in nZEB buildings is a well-studied topic. However, self-shading façades have garnered very little attention [2] . The distribution of solar irradiance on inclined surfaces, due to the plane of the ground, has been theoretically studied in connection with reflected radiation [3] -[5] .
The manner in which irradiance is distributed on walls with a hanging façade, essentially influenced by reflected radiation, should be of interest. The experimental study of the actual distribution supports the expected theoretical model, which is the goal of this study. The theoretical model corresponds to the isotropic sky, which exists in clear-skies and overcast conditions. Under conditions of discrete alternating clouds, the distribution law differs [6] , but it is not discussed in the present study.
2. Theoretical Background
Although solar energy is carried by global radiation, it is expedient to handle it according to its components: beam, diffuse and reflected radiation. It is also expedient to consider including circumsolar diffuse radiation as part of beam radiation, as typical flat-plate solar collectors and walls do not differentiate between them.
In the current research horizontal brightening is assumed to be negligible due to its small share (in an urban environment). In Figure 3 the components of radiation considered in the theoretical model are described, which is created in the vertical plane along the Sun’s current azimuth Φ. G0 is the measured value of irradiance picked up by the horizontal sensor S(0). GFV is the measured value of irradiance picked up by the vertical sensor S(90) at the azimuth “Φ” (turned directly into the Sun). GBV is the measured value of irradiance picked up by the vertical sensor S(−90) at the azimuth “Φ + 180” (turned away from the Sun). Gr is the measured value of irradiance picked up by the backward horizontal sensor S(180)—recording the pure reflected radiation. All these values are known by measurements and can be used as inputs in the calculation. Sensors S(−90) and S(180) are always located in shadow, which means that the beam component is lacking in GBV and Gr. Correspondingly, in the isotropic sky model [7] and isotropic ground model [3] the sum of diffuse and reflected radiation exists on all planes, equally on the illuminated or shadowed side of the carrier ring, where the sensors S(0) - S(180) are installed.
1Of course, if the sun is shining.
Additionally, the beam component exists on the illuminated sector only1 and its value depends on the beam radiation Gb and attack angle ΘT. building the model in the plane of the Sun’s azimuth, a simple relation is valid ΘT = π/2 − αs – β. This knowledge allows a flow diagram of the theoretical calculations to be composed [8] , see Figure 4, where the known variables are the tilt angle β and the Sun’s height angle αs. The flow diagram and text uses values relative to G0, marked with an asterisk
. (1)
When creating the flow diagram, the fact is used that sensor S(−90) is always in shadow, and the sum of the isotropic diffuse and reflected radiation can be expressed as
. (2)
Considering that at β = −90˚ its cosine is zero,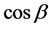 
= 0, it results
, where 
is the albedo. This theoretical model is compared below with actual (measured) relative values of irradiance on the inclined planes in different conditions and on different types of surfaces.
3. Hardware for the Measurements
In order to measure the irradiance on inclined surfaces due to the plane of the ground, a special portable stand was constructed. The stand has a carrier ring with six sensors and a frame, see Figure 5. Sensor S(0) measures global radiation on the horizontal plane G0, sensor S(90) measures the same on the vertical plane GV, and sensor S(180) measures pure reflected radiation Gr. Sensors S(112.5), S(135) and S(157.5) measure radiation on corresponding planes. The whole stand can be turned directly into the Sun’s azimuth Φ, or away from it, or to any free azimuth
;
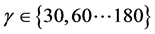. The sensors used were Danish-made photoelectrical pyranometers [9] , which have a transient time of microseconds and allow for the dynamic behavior of (reflected) radiation to be studied.
![]()
Figure 1. A self-shaded façade in Tallinn Estonia (Liivalaia Street).
![]()
Figure 2. A self-shaded façade in Tallinn Estonia (St. Petersburg Highway).
![]()
Figure 3. Components of radiation, which are used in theoretical calculations.
![]()
Figure 4. Flow diagram for the theoretical calculations of relative irradiance on tilted planes.
![]()
Figure 5. Portable stand for measurements.
The height of sensor S(180) is 1.85 m above the ground (1.5 m above the water). Under sunny conditions, a sector (180˚) of the carrier ring is always illuminated by beam radiation, although the position of this illuminated sector depends on the height angle of the Sun αs. The said ring is transported separately and in each measuring session connected to the frame.
The frame has an aluminum vertical post for the carrier ring and two supporting legs under ~30˚ angles. The vertical position of the post can be controlled by a plumb line and rotated around 360˚. In this way, all required azimuths could be controlled.
On weak surfaces: rank grass, thick snow and the (slippery and tilted) bottom of a pond, the operator has to support the frame. The influence of the stand on the accuracy of the measurements is discussed below. Therefore, the accuracy of the vertical position can be evaluated in the range ±5˚. The entire structure of the frame has been painted black, to avoid any possible reflections. The influence of the stand on the accuracy of the measurements is discussed below. Figure 6 shows the complex measurement device for measurements on a limestone gravel surface. Other tested surfaces were snow (fresh and old), asphalt, sand, grass (rank and sparse) and water (still).
4. Methodical Introduction
Measured global irradiance was recorded using a midilogger 200 data logger and the results presented below are the average values of 20 - 30 s recordings in relative units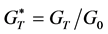
, where GT is irradiance on the tilted plane and G0 is irradiance on the horizontal plane. The first measurements were taken while turned directly into the Sun’s azimuth “Φ” and then the stand was turned clockwise to the next position. Azimuth increments of 30˚ were used, and during simplified measurements this increment was 90˚. Measurements were taken in clear-sky
![]()
Figure 6. Measurements of radiation on a limestone gravel surface.
or in overcast conditions. In some cases, a visor was used to protect S(90) from beam radiation; these measurements will be highlighted with an additional comment. Figure 7 shows the distribution of relative irradiance in clear-sky conditions, on the ground (a cultivated landfill-hill of Tallinn, 59.36˚N, 24.65˚E, 60 m a.s.l.) covered by rank grass, depending on the azimuth and tilt angle.
Due to the practically coinciding lines of the sensors S(135) - S(180) these are united and marked in Figure 7 as “<135”. The diagram in Figure 8 was recorded in a car park with an asphalt surface and it shows the distribution of relative irradiance in overcast conditions, depending on the azimuth and tilt angle.
The diagram in Figure 8 was recorded at the stadium of Tallinn Technical University, which is covered with sparse grass. Dotted grid lines in Figure 7 and Figure 8 mark values 1.2 and 0.6, respectively. The theory of the distribution of irradiance and similar measurements in conditions of discrete alternating cloud requires a special study and is beyond the scope of this paper.
5. Results and Discussion
Comparisons of the calculated and measured values of irradiance under different conditions using relative values are presented in this section. The lines in the following figures mean the following:![]()
—calculated diffuse irradiance on tilted planes;![]()
—calculated reflected irradiance on tilted planes;![]()
—calculated beam irradiance on tilted planes;![]()
—calculated global irradiance on tilted planes;![]()
—measured actual irradiance on tilted planes. For each diagram, recording data and a short comment are added.
The coincidence of ![]()
and ![]()
is good in the shadowed and almost satisfactory in the illuminated sectors (see Figure 9). These measurements were taken on the hill of the closed and cultivated Tallinn landfill, with an absolute unobstructed horizon.
The coincidence of ![]()
and ![]()
is not quite satisfactory due to the Sun being hidden and satisfactory away from the Sun (see Figure 10). These measurements were taken in the stadium of Tallinn University of Technology, surrounded by low forest (height of the optical barrier is ~15˚), and possibly influenced by the (nearest ~70 m) forest.
The coincidence of ![]()
and ![]()
is good (see Figure 11) both in the shadowed and the illuminated sectors. These measurements were taken in the car park of a shopping center.
![]()
Figure 7. Dependence of irradiance on azimuth Φ and tilt angle ![]()
in sunshine.
![]()
Figure 8. Dependence of irradiance on azimuth Φ and tilt angle ![]()
in shadow.
![]()
Figure 9. Rank grass in sunshine: G0 = 793 Wm−2; αs = 44.8˚ and ![]()
= 0.21.
![]()
Figure 10. Sparse grass under an overcast sky (in shadow): G0 = 187 Wm−2; αs =39.4˚ and ![]()
= 0.18.
The coincidence of ![]()
and ![]()
is not quite satisfactory (see Figure 12), due to the Sun being hidden, and satisfactory away from the Sun. Possibly the result is distorted due to several large trucks being parked at a distance of ~50 m.
The coincidence of ![]()
and ![]()
is good in the shadowed and not quite as satisfactory in the illuminated sectors (see Figure 13).
The coincidence of ![]()
and ![]()
is good in both the shadowed and the illuminated sectors (see Figure 14).
In this experiment, S(90) was covered with an upper visor which blocked beam radiation.
It is shown that irradiance in the vertical plane @S(90) is now less than the pure reflected irradiance measured with S(180), which coincides with the theoretical model. The coincidence of ![]()
and ![]()
is good in both the shadowed and the illuminated sectors (see Figure 15).
The coincidence of ![]()
and ![]()
is very good in both the shadowed and the illuminated sectors (see Figure 16).
The coincidence of ![]()
and ![]()
is very good in the shadowed sector (see Figure 17), but it is principally different in the illuminated sector. It is not a failure: this experiment was repeated three times and in different locations; however, the results were always similar (presented in Figure 17).
Along the Sun’s beams, reflection from the snow is a mirror-like reflection. In the opposite direction it is diffuse. The same quality also exists in the case of fresh snow.
![]()
Figure 11. Asphalt surface in sunshine: G0 = 607 Wm−2; αs = 46.8˚ and ![]()
= 0.17.
![]()
Figure 12. Asphalt surface under an overcast sky (in shadow): G0 = 189 Wm−2; αs = 49.5˚ and ![]()
= 0.15.
![]()
Figure 13. Gravel surface (Figure 6) in sunshine: G0 = 679 Wm−2; αs = 52.5˚ and ![]()
= 0.19.
![]()
Figure 14. The same gravel surface in sunshine using a visor for S(90): G0 = 679 Wm−2; αs = 52.5˚ and ![]()
= 0.19.
![]()
Figure 15. Sandy surface in sunshine: G0 = 705 Wm−2; αs = 44.5˚ and![]()
= 0.19.
![]()
Figure 16. Water in sunshine: G0 = 798 Wm−2; αs = 46.4˚ and ![]()
= 0.07.
![]()
Figure 17. old snow in sunshine: G0 = 585 Wm−2; αs = 34.2˚ and ![]()
= 0.7.
6. Reliability of the Experiment
Figure 18 shows the stand for the measurements of the reflected radiation at the Toravere Actinometrical Station [10] , which is a part of the Baseline Solar Radiation Network (BSRN, [11] ) and uses standard equipment. The sensor on the reverse horizontal plane is located away from surrounding objects and supported by a heavy console, the construction of which cannot be realized under portable conditions. Therefore, it may be that the stand used by us includes a systematic error. To prove the lack of such an error, the following test was conducted.
The free carrier ring alone was hung from a cable (at a height of 2 m) over a grass surface (case A) and the irradiance of each sensor was recorded. Then the frame was placed in its position, legs under the ring (case B) and away from the ring (case C) and the recording was repeated.
Figure 19 shows the result of the control: recorded irradiance in relative units based on S(0) of case A proves that the frame (plus operator) does not influence the results (or a possible influence remains within the range of random errors). Therefore, it can be considered that the use of a portable measuring device does not involve systematic errors and the results are reliable.
7. Conclusion
The study proves that the isotropic sky and isotropic ground reflection model warrants calculated values of irradiance in relative units on surfaces inclined due to the ground, which have a good coincidence with their actual values. Usage of the work—measuring current values of the global irradiance on different planes allows the study of the current distribution of irradiance on inclined surfaces (in the real time domain). The said coincidence is
![]()
Figure 18. The stand for the measurements of reflected radiation at the Toravere Actinometrical Station (TOR).
![]()
Figure 19. Influence of the frame on the result is lacking.
the best at low albedo, but is not valid for snow-cover due to the Sun. The distribution of irradiance on inclined surfaces with alternating discrete clouds has to be studied specifically.
Nomenclature
A = Gr/G0—albedo
G, Wm−2—irradiance
G0, Wm−2—irradiance on the horizontal plane
Ga, Wm−2—measured actual irradiance on tilted planes
Gb, Wm−2—irradiance of the beam radiation
Gb0, Wm−2—beam component of irradiance on the horizontal plane
Gd0, Wm−2—diffuse component of irradiance on the horizontal plane
GVB, Wm−2—rradiance on the (shadowed) vertical plane
GVF, Wm−2—irradiance on the (illuminated) vertical plane
GT, Wm−2—relative irradiance on the on an inclined plane
GbT, Wm−2—beam component of irradiance on an inclined plane
GdT, Wm−2—diffuse component of irradiance on an inclined plane
Gr, Wm−2—reflected irradiance on the reverse horizontal plane
GrT, Wm−2—calculated reflected irradiance on tilted planes
GbT, Wm−2—calculated beam irradiance on tilted planes
GT, Wm−2—calculated global irradiance on tilted planes
Corresponding relative values are marked with asterisk: G* = G/G0—relative irradiance
αs—height angle of sun
ΘT—incident angle of the beam radiation