Application of Operational Approaches to Solving Decision Making Problem Using Z-Numbers ()
1. Introduction
Decision making is constantly needed in the real world. In many situations, making choices depending on numerous factors limited to human ability is very difficult to deal with. In a fuzzy environment, a standard method to express experts’ preferences usually uses numerical values assessed in an interval from zero to one. However, there are some difficult decisions where experts are not able to give exact numerical values to their preferences. In such cases, linguistic assessments are alternatively used instead of numerical values to express preference [1] -[3] . In [4] a new characterization of consistency based on the additive transitivity property of fuzzy preference relations has been proposed. This new characterization allows us to easily check the consistency between the experts’ opinions. Experts’ opinions are represented by using if-then rules. In [5] one of the knowledge discovery approach-linguistic summarization [6] -[8] approach to generate if-then rules for causal databases is proposed. Both type-1 and interval type-2 fuzzy sets are considered. In a lot of technical literature [9] -[13] fivequality measures—the degree of truth, sufficient coverage, reliability, outlier and simplicity are defined. Among them the degree of reliability is especially valuable for finding the most reliable and representative rules.
In [14] Zadeh introduced the concept of Z-numbers to describe the uncertain information which is a more generalized notion. A Z-number is an ordered pair of fuzzy numbers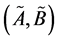 . Here
. Here 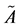 is a value of some variable and
is a value of some variable and  represents an idea of certainty or other closely related concept such as sureness, confidence, reliability, strength of truth, or probability. It should be noted that in everyday decision making most decisions are in the form of Z-numbers. Zadeh suggests some operations for computation with Z-numbers, using the extension principle. On Z-valuation using Zadeh’s Z-numbers problem is discussed in [15] by R. Yager. It was shown how to use these Z-numbers to provide information about an uncertain variable in the form of Z-valuations, assuming that this uncertain variable is random. Yager offers an illustration of a Z-valuation, showing how to make decisions and answer questions. It has also been discussed the relationship between Z-numbers and linguistic summaries [16] . Author of [15] has provided for a representation of Z-valuations in terms Dempster-Shafer belief structures [17] , that made use of type-2 fuzzy sets. In [18] a method of converting Z-number to classical fuzzy number has been discussed. Decision making using Z-numbers under Uncertain Environment is discussed in [19] . Authors for solving multi-criteria decision making problem using Z-numbers have converted Z-numbers to classical fuzzy number and a priority weight of each alternative is determined.
represents an idea of certainty or other closely related concept such as sureness, confidence, reliability, strength of truth, or probability. It should be noted that in everyday decision making most decisions are in the form of Z-numbers. Zadeh suggests some operations for computation with Z-numbers, using the extension principle. On Z-valuation using Zadeh’s Z-numbers problem is discussed in [15] by R. Yager. It was shown how to use these Z-numbers to provide information about an uncertain variable in the form of Z-valuations, assuming that this uncertain variable is random. Yager offers an illustration of a Z-valuation, showing how to make decisions and answer questions. It has also been discussed the relationship between Z-numbers and linguistic summaries [16] . Author of [15] has provided for a representation of Z-valuations in terms Dempster-Shafer belief structures [17] , that made use of type-2 fuzzy sets. In [18] a method of converting Z-number to classical fuzzy number has been discussed. Decision making using Z-numbers under Uncertain Environment is discussed in [19] . Authors for solving multi-criteria decision making problem using Z-numbers have converted Z-numbers to classical fuzzy number and a priority weight of each alternative is determined.
The paper is organized as follows. Section 2 discusses required definitions. The algorithm of proposed decision making method is presented in Section 3. Description of portfolio selection-real-life business problem and the experimental results of calculations are described in Section 4. In Section 5 given basic steps of the operational approach (OA) to solving the problem selection of a vehicle. The conclusion is presented in Section 6.
2. Mathematical Definition and Notation
Definition 1. A Z-number [14]
A Z-number is an ordered pair of fuzzy numbers,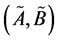 .
. 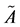 is a fuzzy restriction on the values which a real-valued uncertain variable is allowed to take.
is a fuzzy restriction on the values which a real-valued uncertain variable is allowed to take.  is a measure of reliability of the first component (Figure 1).
is a measure of reliability of the first component (Figure 1).
Definition 2 [9] . A triangular fuzzy number  can be defined by a a triplet
can be defined by a a triplet , where the membership can be determined as the following equation:
, where the membership can be determined as the following equation:

Definition 3 [9] . A fuzzy set A is defined on a universe X may be given as:

where  is the membership function. A membership value
is the membership function. A membership value  describes the degree of belongingness of
describes the degree of belongingness of  in A.
in A.
Definition 4. Let  and
and  be two triangular fuzzy numbers. The graded mean integration representation of triangular fuzzy numbers
be two triangular fuzzy numbers. The graded mean integration representation of triangular fuzzy numbers  and
and  can be obtained [20] , respectively, as follows:
can be obtained [20] , respectively, as follows:
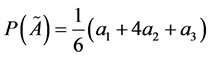

The canonical representation of the multiplication operation on triangular fuzzy numbers  and
and  is defined as:
is defined as:

Definition 5 [19] . The priority weight of each alternative can be defined as follows:
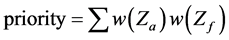
where  is the weight of the criteria, and
is the weight of the criteria, and  is the value of each criteria.
is the value of each criteria.
Definition 6. Sum of two independent normal random variables [21] . Let X and Y be two independent normal random variables with probability density functions
 and
and  respectively. The sum Z = X + Y of X and
respectively. The sum Z = X + Y of X and  is a random variable whose density function
is a random variable whose density function  is defined as follows:
is defined as follows:

Definition 7. Product of two normal density functions. The product  of two density functions
of two density functions 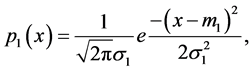 and
and  is a normal density function with mean and variance given by
is a normal density function with mean and variance given by

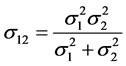
For simplicity we will denote  as
as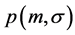 .
.
Definition 8. Fuzzy probability [22] [23] . Let a discrete random variable  takes a value from the set
takes a value from the set . The fuzzy numbers
. The fuzzy numbers  are called the fuzzy probabilities of
are called the fuzzy probabilities of  if for any
if for any
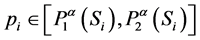 there exist
there exist ,
,
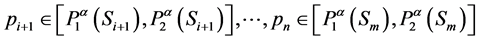 such that
such that

where  is an
is an  -cut of a fuzzy number
-cut of a fuzzy number 
3. Algorithm of Decision Making Method Using Z-Numbers
Algorithm of decision making method using Z-numbers under uncertain environment is as follows:
Step 1. Construct the fuzzy decision making matrix for decision making problem.
Step 2. Transform the linguistic value to numerical value.
Step 3. Normalize the fuzzy decision making matrix.
Step 4. Convert the Z-numbers to crisp number.
Step 5. Determine the priority weight of each alternative.
4. Statement of the Decision Problem
As it is known, portfolio selection problem is one of standard and most important problems in investment and financial research fields. Portfolio selection—real-life business problem is characterized by the following three conditions:
1. Economy declines;
2. No change;
3. Economy expands.
Let us give formal description of the portfolio selection problem as a problem of decision making with imprecise probabilities described as Z-numbers.
1) State of nature. States of nature are represented by the three economic conditions. During the portfolio selection it is very important to properly identify the economic condition. Taking this into account it is adequately to describe the economic condition by using Z-numbers. The set of states of nature  described Z-numbers are Economy declines—
described Z-numbers are Economy declines— :
: 
No change— :
:
Economy expands— :
: 
2) Alternatives.
Alternatives are represented by the three acts (selection A, B, C).
3) Utilities.
Utility of an alternatives for each state is described by Z-numbes. So, we will formulate portfolio selection method by using Z-numbers as a determination of the priority weight of each alternative.
Portfolio Selection—Real-Life Business Problem
Here we give an example portfolio selection—real-life business problem. An investor has a certain amount of money available to invest now. Three alternative portfolio selections are available. The estimated profits of each portfolio under each economic condition are indicated in the following payoff Table 1 by using Z-valuation:
Let  be a fuzzy set of the universe of discourse X subjectively defined as follow:
be a fuzzy set of the universe of discourse X subjectively defined as follow:



Table 1. Payoff table for Portfolio selection-real-life business problem.
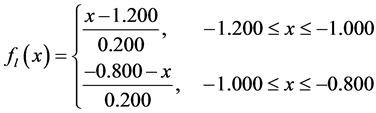
 (1)
(1)




where  are the membership functions of the fuzzy sets.
are the membership functions of the fuzzy sets.
Fuzzy restriction part of Z-numbers by Scale data is given as Table 2:
The problem is to determine portfolio selection. On the basis of his own past experience, the investor assigns the following probabilities to each economic condition:
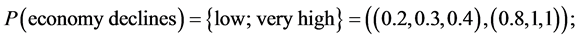


There are three different choices, namely A, B, C.
Alternative 1: 
Alternative 2: 
Alternative 3: 
Take the three main criteria (Economy declines, No change, Economy expands) into consideration.
At second step according to the membership function denoted by Equation (1) the linguistic variable can be converted to numerical value.
Decision variables with numerical values is described as the following form:
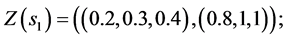





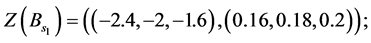
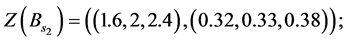




And the third step is to normalize the fuzzy data to avoid complexity of mathematical operations in the decision process. The normalized data for decision variables are:
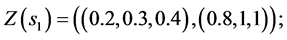











Values of decision variables which combine the restraint and reliability will be described as follows:
Alternative 1:
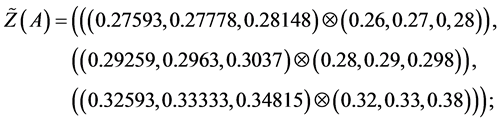 (2)
(2)
Alternative 2:

Alternative 3:

The fourth step is convert Z-number to crisp number. After normalizing the weight of criteria, we can get the final priority weight of the three Portfolio denoted by matrix 4 which is getting by using matrix 3.
By using definition 4 decision matrix with crisp number obtained with the following form:
 (3)
(3)
Matrix of the priority weight is represented by (4):
 (4)
(4)
Finally, we calculated the priority weight for each alternative and obtained the following results:
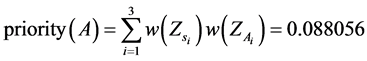


So, the best alternative is C as one with the highest priority weight.
5. Application of OA to Solving Decision Making Problem with Z-Numbers
5.1. Statement of Problem
Let  be a set of states of nature,
be a set of states of nature,  be a set of Znumber-valued outcomes. Linguistic information on likelihood
be a set of Znumber-valued outcomes. Linguistic information on likelihood  of the states of nature is represented by Z-valued probabilities
of the states of nature is represented by Z-valued probabilities  of the states
of the states :
:

The problem of decision making with Z-valued information on the base of EU consists in determination of an optimal act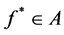 :
:
Find  for which
for which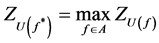 .
.
Here  is a Z-valued expected utility defined as
is a Z-valued expected utility defined as
 where multiplication and addition are defined as in [14] .
where multiplication and addition are defined as in [14] .
5.2. Basic Steps of Operational Approach
Operational approach to solving decision making problem with Z-numbers is described in [22] . Basic steps of operational approach is shown below:
Step 1. Given Z-valued outcome

of an alternative  at a state of nature
at a state of nature 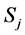 and a Z-valued probability
and a Z-valued probability 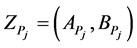 of a state of nature
of a state of nature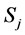 , calculate
, calculate

The calculation of  is done as follows.
is done as follows.
Step 2. Convert Z numbers 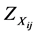 and
and  to Z+ numbers:
to Z+ numbers:


2.1. Calculate 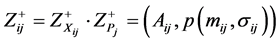
2.2. Calculate .
.
For calculation of  we have to solve the following problem:
we have to solve the following problem:
 subject to
subject to

2.3. Calculate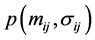 :
:
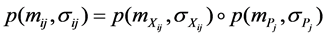 ,
,

For simplicity, we denote 
2.4. Calculate 
For calculation of , it is need at first to calculate the following expressions:
, it is need at first to calculate the following expressions:

and

Then  is calculated by solving the following optimization problem:
is calculated by solving the following optimization problem:


subject to

2.5. Calculate 
 is calculated by solving the following optimization problem:
is calculated by solving the following optimization problem:

subject to

As a result of calculations at step 2, 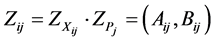 is obtained.
is obtained.
Step 3. At this step, given Z-numbers  obtained at the previous step, the Z-valued Expected Utility
obtained at the previous step, the Z-valued Expected Utility

is calculated as it is shown below:
3.1. Convert Z numbers  to Z+ numbers.
to Z+ numbers.


3.2. Calculate 
3.3. Calculate 
 is calculated by solving the following optimization problem:
is calculated by solving the following optimization problem:
 subject to
subject to

3.4. Calculate .
.
 is calculated as follows.
is calculated as follows.
 . For simplicity, we denote
. For simplicity, we denote 
3.5. Calculate .
.
For calculation of , we need to calculate the following values:
, we need to calculate the following values:

And

Then  is calculated by solving the following optimization problem:
is calculated by solving the following optimization problem:

3.6. Calculate 
 is calculated by solving the following optimization problem:
is calculated by solving the following optimization problem:

subject to
 .
.
As a result of calculations at stage 3, Z-value 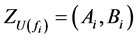 of the EU for alternative
of the EU for alternative  is obtained.
is obtained.
5.3. Example. Selection of a Vehicle
In this section, we provide an example of selection of a vehicle for journey to illustrate application of the operational approach to solving decision making problem with Z-information. Three alternatives are considered: car, taxi and train. Three states of nature are considered at which the alternatives are evaluated taking into account price, journey time, comfort. The payoff table for the considered decision problem with Z-valued information is given in Table 3.
The obtained Z-values of the utility function for alternatives ,
,  ,
,  are the following:
are the following:
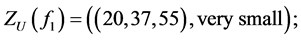
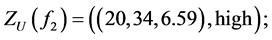
 .
.
6. Conclusion
Z-number is a new notion proposed by Zadeh has more ability to describe the uncertain knowledge. In this paper, we solve the multi-criteria decision making using Z-number and an algorithm is proposed to deal with the Z-number. At last, a numerical example is used to illustrate to procedure of the applied approaches. In the present work generalized the Expected Utility theory to the case of Z-valued information. An operational ap

Table 3. Payoff table for selection of a vehicle problem.
proach with detailed computational procedures is developed for this purpose. The operational approach is applied to solve a problem of decision making on a selection of a vehicle for journey with Z-valued information.