1. Introduction
For positive integers 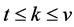 and
and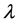 , we define a
, we define a 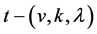 design to be a finite incidence structure
design to be a finite incidence structure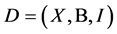 , where
, where 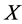 denotes a set of points,
denotes a set of points, 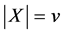 and
and 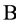 a set of blocks,
a set of blocks, 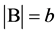 , with the properties that each block
, with the properties that each block 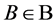 is incident with k points, and each t-subset of
is incident with k points, and each t-subset of 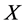 is incident with
is incident with 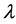 blocks. A flag of
blocks. A flag of 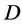 is an incident point-block pair, that is
is an incident point-block pair, that is 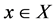 and
and 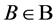 such that
such that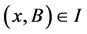 . We consider automorphisms of
. We consider automorphisms of 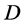 as pairs of permutations on X and B which preserve incidence, and call a group
as pairs of permutations on X and B which preserve incidence, and call a group 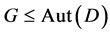 of automorphisms of
of automorphisms of 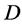 flag-transitive (respectively block-transitive, point t-transitive, point t-homogeneous), if G acts transitively on the flags (respectively transitively on the blocks, t-transitively on the points, t-homogeneous on the points) of
flag-transitive (respectively block-transitive, point t-transitive, point t-homogeneous), if G acts transitively on the flags (respectively transitively on the blocks, t-transitively on the points, t-homogeneous on the points) of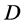 . It is a different problem in Combinatorial Maths how to construct a design with given parameters. In this paper, we shall take use of the automorphism groups of designs to find some new designs.
. It is a different problem in Combinatorial Maths how to construct a design with given parameters. In this paper, we shall take use of the automorphism groups of designs to find some new designs.
In recent years, the classification of flag-transitive Steiner 2-designs has been completed by W. M. Kantor (See [1] ), F. Buekenhout, A. De-landtsheer, J. Doyen, P. B. Kleidman, M. W. Liebeck, J. Sax (See [2] ); for flagtransitive Steiner t-designs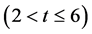 , Michael Huber has done the classification (See [3] -[7] ). But only a few people have discussed the case of flag-transitive t-designs where
, Michael Huber has done the classification (See [3] -[7] ). But only a few people have discussed the case of flag-transitive t-designs where 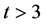 and
and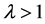 .
.
In this paper, we may study a kind of flag-transitive designs with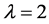 . We may consider this problem by making use of the classification of the finite 3-homogeneous permutation groups to study flag-transitive
. We may consider this problem by making use of the classification of the finite 3-homogeneous permutation groups to study flag-transitive 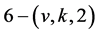 designs. Our main result is:
designs. Our main result is:
Theorem: There are no non-trivial 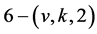 designs
designs  admitting a flag transitive group
admitting a flag transitive group 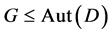 of automorphisms.
of automorphisms.
2. Preliminary Results
Lemma 2.1. (Huber M [4] ) Let 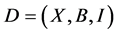 be a
be a 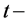 design with
design with 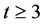 .If
.If 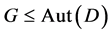 acts flag-transitively on
acts flag-transitively on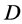 , then G also acts point 2-transitively on
, then G also acts point 2-transitively on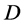 .
.
Lemma 2.2. (Cameron and Praeger [8] ). Let 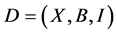 be a
be a 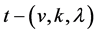 design with
design with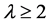 . Then the following holds:
. Then the following holds:
(1) If 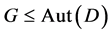 acts block-transitively on
acts block-transitively on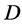 , then
, then 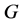 also acts point
also acts point 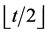 -homogeneously on
-homogeneously on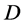 ;
;
(2) If 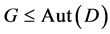 acts flag-transitively on
acts flag-transitively on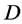 , then
, then 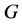 also acts point
also acts point 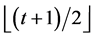 -homogeneously on
-homogeneously on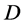 .
.
Lemma 2.3. (Huber M [9] ) Let 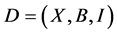 be a
be a 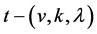 design. If
design. If 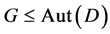 acts flag-transitively on
acts flag-transitively on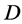 , then , for any
, then , for any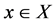 , the division property
, the division property 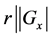 holds.
holds.
Lemma 2.4. Let 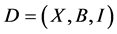 be a
be a 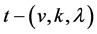 design. Then the following holds:
design. Then the following holds:
(1)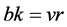 ;
;
(2)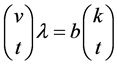 ;
;
(3) For 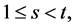 a
a 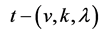 design is also an
design is also an 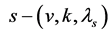 design, where
design, where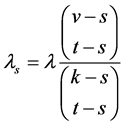 .
.
(4) In particular, if t = 6, then
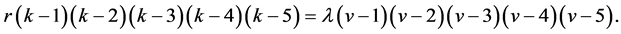
Lemma 2.5. (Beth T [10] ) If 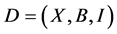 is a non-trivial
is a non-trivial 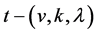 design, then
design, then 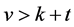
Lemma 2.6. (Wei J L [11] ) If 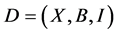 is a
is a 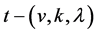 design, then
design, then
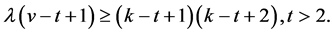
In this case, when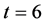 , we deduce from Lemma 2.6 the following upper bound for the positive integer
, we deduce from Lemma 2.6 the following upper bound for the positive integer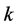 .
.
Corollary 2.7. Let 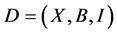 be a non-trivial
be a non-trivial 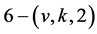 design, then
design, then
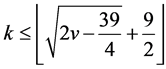 .
.
Proof: By Lemma 2.6, when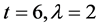 , we have
, we have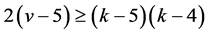 , then
, then
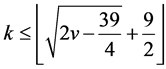 .
.
Remark 2.8. Let 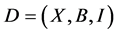 be a non-trivial
be a non-trivial 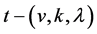 design with
design with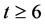 . If
. If 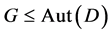 acts flagtransitively on
acts flagtransitively on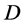 , then by Lemma 2.2 (1),
, then by Lemma 2.2 (1), 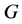 acts point 3-homogeneously and in particular point 2-transitively on
acts point 3-homogeneously and in particular point 2-transitively on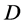 . Applying Lemma 2.4 (2) yields the equation
. Applying Lemma 2.4 (2) yields the equation
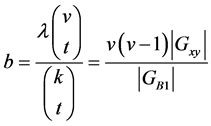
where 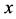 and
and 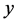 are two distinct points in
are two distinct points in 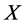 and
and 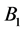 is a block in
is a block in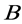 . If
. If 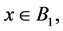 then
then
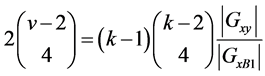 .
.
Corollary 2.9 Let 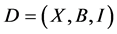 be a
be a 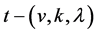 design, then
design, then
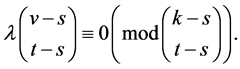
For each positive integers,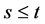 .
.
Let G be a finite 3-homogeneous permutation group on a set X with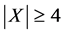 . Then
. Then 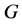 is either of
is either of
(A) Affine Type:
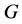 contains a regular normal subgroup
contains a regular normal subgroup 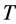 which is elementary Abelian of order
which is elementary Abelian of order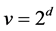 .If we identify
.If we identify 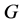 with a group of affine transformations
with a group of affine transformations
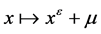
Of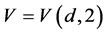 , where
, where 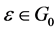 and
and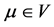 , then particularly one of the following occurs:
, then particularly one of the following occurs:
(1) 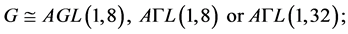
(2)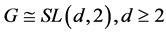 ;
;
(3)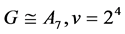 ;
;
or
(B) Almost Simple Type: 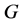 contains a simple normal subgroup
contains a simple normal subgroup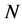 , and
, and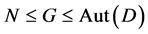 . In particular, one of the following holds, where
. In particular, one of the following holds, where 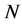 and
and 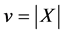 are given as follows:
are given as follows:
(1) 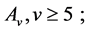
(2) 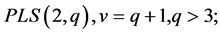
(3) 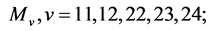
(4)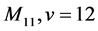 .
.
3. Proof of the Main Theorem
Let 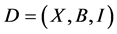 be a non-trivial
be a non-trivial 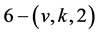 design,
design, 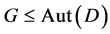 acts flag-transitively on
acts flag-transitively on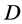 , by lemma 2.2,
, by lemma 2.2, 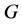 is a finite 3-homogeneous permutation group. For
is a finite 3-homogeneous permutation group. For 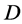 is a non-trivial
is a non-trivial 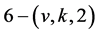 design, then
design, then 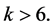 We will prove by contradiction that
We will prove by contradiction that 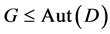 cannot act flag-transitively on any non-trivial
cannot act flag-transitively on any non-trivial 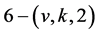 design.
design.
3.1. Groups of Automorphisms of Affine Type
Case (1): 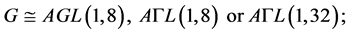
If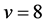 , then Lemma 2.5 yields
, then Lemma 2.5 yields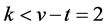 , a contradiction to
, a contradiction to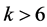 . For
. For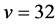 , Corollary 2.7 implies
, Corollary 2.7 implies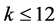 . Thus
. Thus 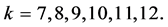 By Lemma 2.4 we have
By Lemma 2.4 we have
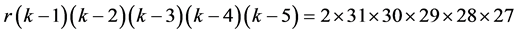
for each values of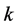 , we have
, we have
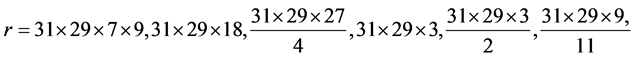
but  is a positive integer, thus
is a positive integer, thus  On the other hand, we have
On the other hand, we have  , those are contradicting to Lemma 2.3.
, those are contradicting to Lemma 2.3.
Case (2): .
.
Here 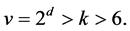 For
For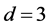 , we have
, we have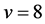 , already ruled out in Case (1). So we may assume that
, already ruled out in Case (1). So we may assume that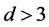 . Any six distinct points being non-coplanar in
. Any six distinct points being non-coplanar in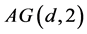 , they generate an affine subspace of dimension at least 3. Let
, they generate an affine subspace of dimension at least 3. Let 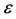 be the 3-dimensional vector subspace spanned by the first three basis vectors
be the 3-dimensional vector subspace spanned by the first three basis vectors 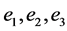 of the vector space
of the vector space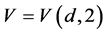 . Then the point-wise stabilizer of
. Then the point-wise stabilizer of 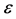 in
in 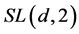 (and therefore also in
(and therefore also in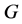 ) acts point-transitively on
) acts point-transitively on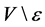 . Let
. Let 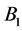 and
and 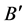 be the two blocks which are incident with the 6-subset
be the two blocks which are incident with the 6-subset 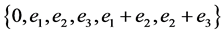 , If the block
, If the block  contains some point
contains some point 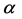 of
of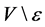 , then
, then 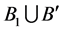 contains all points of
contains all points of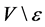 , and so
, and so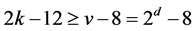 , this yields
, this yields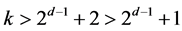 , a contradiction to Lemma 2.6. Hence
, a contradiction to Lemma 2.6. Hence 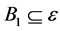 and
and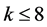 . On the other hand, for
. On the other hand, for 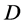 is a flag-transitive 6-design admitting
is a flag-transitive 6-design admitting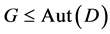 we deduce from [[12] , prop.3.6 (b)] the necessary condition that
we deduce from [[12] , prop.3.6 (b)] the necessary condition that 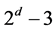 must divide
must divide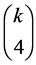 , and hence it follows for each respective value of
, and hence it follows for each respective value of 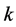 that
that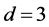 , contradicting our assumption.
, contradicting our assumption.
Case (3): 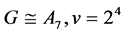
For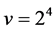 , we have
, we have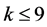 , by Corollary 2.7. By Lemma 2.4 and Lemma 2.3, we have
, by Corollary 2.7. By Lemma 2.4 and Lemma 2.3, we have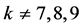 .
.
3.2. Groups of Automorphisms of Almost Simple Type
Case (1): 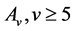
Since 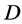 is non-trivial with
is non-trivial with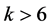 , we may assume that
, we may assume that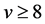 . Then
. Then 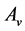 is 6-transitive on
is 6-transitive on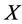 , and hence
, and hence 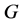 is
is 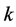 -transitive, this yields
-transitive, this yields 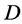 containing all of the
containing all of the 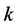 -subset of
-subset of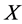 . So
. So 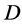 is a trivial design, a contradiction.
is a trivial design, a contradiction.
Case (2): 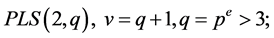
Here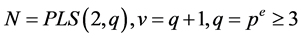 and
and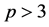 , so
, so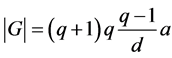
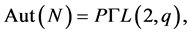 with
with 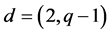 and
and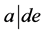 . We may again assume that
. We may again assume that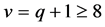 .
.
We will first assume that . Then, by Remark 2.8, we obtain
. Then, by Remark 2.8, we obtain
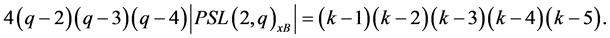 (1)
(1)
In view of Lemma 2.6, we have
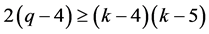 (2)
(2)
It follows from Equation (1) that
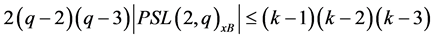 (3)
(3)
If we assume that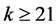 , then obviously
, then obviously
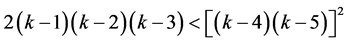
and hence
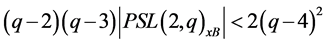
In view of inequality (2), clearly, this is only possible when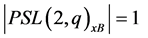 . In particular,
. In particular, 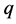 has not to be even. But then the right-hand side of Equation (1) is always divisible by 16 but never the left-hand side, a contradiction. If
has not to be even. But then the right-hand side of Equation (1) is always divisible by 16 but never the left-hand side, a contradiction. If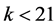 , then the few remaining possibilities for
, then the few remaining possibilities for 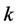 can easily be ruled out by hand using Equation (1), Inequality (2), and Corollary 2.9.
can easily be ruled out by hand using Equation (1), Inequality (2), and Corollary 2.9.
Now, let us assume that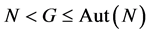 . We recall that
. We recall that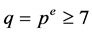 , and will distinguish in the following the case
, and will distinguish in the following the case 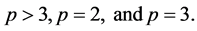
First, let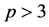 . We define
. We define 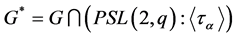 with
with 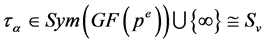 of order
of order 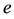
induced by the Frobenius automorphism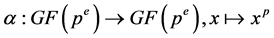 . Then, by Dedekind’s law, we can write
. Then, by Dedekind’s law, we can write
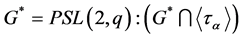
Defining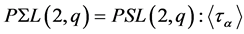 , it can easily be calculated that
, it can easily be calculated that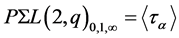 , and
, and 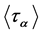 has precisely
has precisely 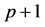 distinct fixed points (cf. e.g., [[13] Ch. 6.4, Lemma 2]). As
distinct fixed points (cf. e.g., [[13] Ch. 6.4, Lemma 2]). As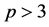 , we have therefore that
, we have therefore that 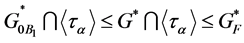 for a flag
for a flag 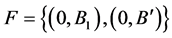 fixed with
fixed with 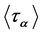 by the definition of
by the definition of 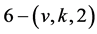 designs. On the other hand, every element of
designs. On the other hand, every element of 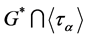 either fixes block
either fixes block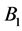 , or commute block
, or commute block 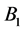 with block
with block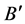 , thus the index
, thus the index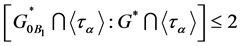 . Clearly
. Clearly 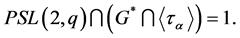
Hence, we have
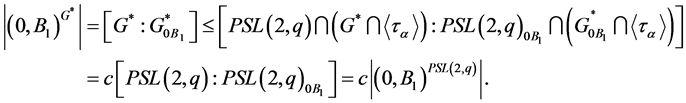
where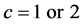 . Thus, if we assume that
. Thus, if we assume that 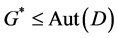 acts already flag-transitively on
acts already flag-transitively on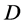 , then we obtain
, then we obtain
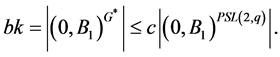 Then either
Then either 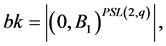 and
and 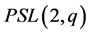 acts on
acts on 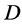 flag-transitively, that is the case when
flag-transitively, that is the case when ; or
; or 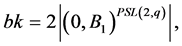 and
and 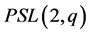 has exactly two orbits of equal length on the sets of flags. Then, proceeding similarly to the case
has exactly two orbits of equal length on the sets of flags. Then, proceeding similarly to the case  for each orbit on the set of the flags, we have that
for each orbit on the set of the flags, we have that
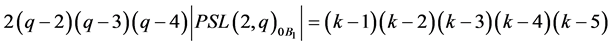 (4)
(4)
Using again
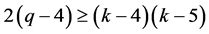 (5)
(5)
We obtain
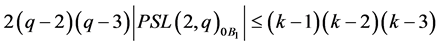 (6)
(6)
If we assume that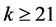 , then again
, then again
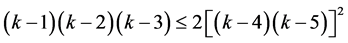 (7)
(7)
and thus
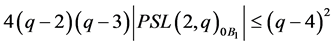
but this is impossible. The few remaining possibilities for 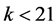 can again easily be ruled out by hand.
can again easily be ruled out by hand.
Now, let 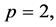 then, clearly
then, clearly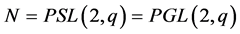 , and we have
, and we have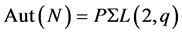 . If we assume that
. If we assume that 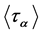 is the subgroup of
is the subgroup of 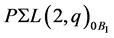 for a flag
for a flag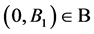 , then we have
, then we have 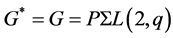 and as clearly
and as clearly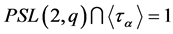 , we can apply Equation
, we can apply Equation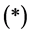 . Thus,
. Thus, 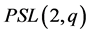 must also be flagtransitive, which has already been considered. Therefore, we assume that
must also be flagtransitive, which has already been considered. Therefore, we assume that 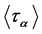 is not the subgroup of
is not the subgroup of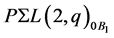 . Let
. Let
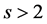 be a prime divisor of
be a prime divisor of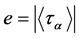 . As the normal subgroup
. As the normal subgroup 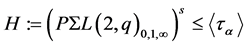 of index
of index 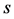
has precisely 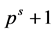 distinct fix points, we have
distinct fix points, we have 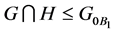 for a flag
for a flag 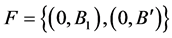 fixed with
fixed with 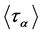 by the definition of
by the definition of 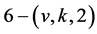 designs. It can then be deduced that
designs. It can then be deduced that 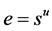 for some
for some 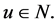 Since if we assume for
Since if we assume for 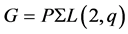 that there exists a further prime divisor
that there exists a further prime divisor 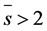 of
of 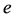 with
with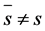 , then
, then
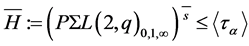 and
and 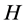 are both subgroups of
are both subgroups of 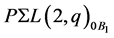 by the flag-transitivity of
by the flag-transitivity of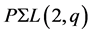 , and hence
, and hence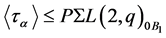 , a contradiction. Furthermore, as
, a contradiction. Furthermore, as 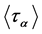 is not the subgroup of
is not the subgroup of
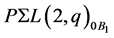 . We may, by applying Dedekind’s law, assume that
. We may, by applying Dedekind’s law, assume that
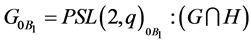
Thus, by Remark 2.8, we obtain
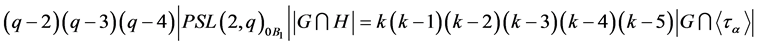
More precisely:
(A) if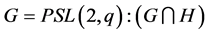 ,
,
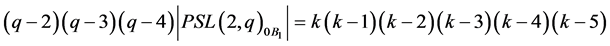
(B) if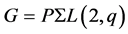 ,
,
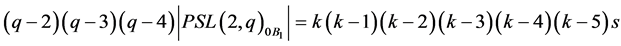
As far as condition (A) is concerned, we may argue exactly as in the earlier case . Thus, only condition (B) remains. If
. Thus, only condition (B) remains. If 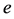 is a power of 2, then Remark 2.8 gives
is a power of 2, then Remark 2.8 gives
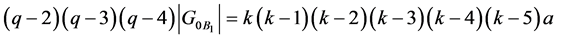
with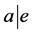 . In particular,
. In particular, 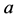 must divide
must divide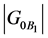 , and we may proceed similarly as in the case
, and we may proceed similarly as in the case , yielding a contradiction.
, yielding a contradiction.
The case 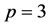 may be treated as the case
may be treated as the case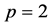 .
.
Case (3): 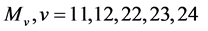
By Corollary 2.7, we get 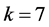 for
for 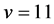 or 12, and
or 12, and 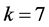 or 8 for
or 8 for 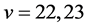 or 24, and the very small number of cases for
or 24, and the very small number of cases for 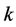 can easily be eliminated by hand using Corollary 2.9 and Remark 2.8.
can easily be eliminated by hand using Corollary 2.9 and Remark 2.8.
Case (4): 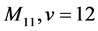
As in case (3), for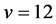 , we have
, we have 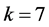 in view of Corollary 2.7, a contradiction since no 6-(12, 7, 2) design can exist by Corollary 2.9. This completes the proof of the Main Theorem.
in view of Corollary 2.7, a contradiction since no 6-(12, 7, 2) design can exist by Corollary 2.9. This completes the proof of the Main Theorem.
Acknowledgements
The authors thank the referees for their valuable comments and suggestions on this paper.