1. Introduction
In this note, we generalize the  value [1] [2] for efficient values for TU (transferable utility) games with a cooperation structure (graph on the set of players; CO games and CO value) like the Myerson value [3] , the position value [4] , and the average tree solution [5] . This value determines payoffs in weighted hierarchical games. Modelling hierarchies in games of cooperative game theory is one step to analyze firms in the framework of cooperative game theory. A first step for this was done by Kalai and Samet [6] using ordered partitions and weights to model hierarchies. Another approach comes from Winter [7] using a sequence of bargaining components [8] to model hierarchies. These values can model levels in the sense of Lazear and Rosen [9] , Carmichael [10] , and Prendergast [11] . The problem of both approaches is that they could not model a clear manager-subordinate structure. Such a structure is a main element of hierarchies in firms [12] [13] . Another approach to model hierarchies might be games with an undirected graph/network on the set of players [3] -[5] . The problem is: all players are symmetrical in the graph; all players are in one level. The paper by van den Brink [14] uses a directed graph/permission structure on the set of players to analyze the effects of hierarchies on players’ payoffs. The basic idea is that a player needs approval from all predecessors. The approach was outlined in Gilles, Owen, and van den Brink [15] . The axiomatization is carried out by van den Brink and Gilles [16] .
value [1] [2] for efficient values for TU (transferable utility) games with a cooperation structure (graph on the set of players; CO games and CO value) like the Myerson value [3] , the position value [4] , and the average tree solution [5] . This value determines payoffs in weighted hierarchical games. Modelling hierarchies in games of cooperative game theory is one step to analyze firms in the framework of cooperative game theory. A first step for this was done by Kalai and Samet [6] using ordered partitions and weights to model hierarchies. Another approach comes from Winter [7] using a sequence of bargaining components [8] to model hierarchies. These values can model levels in the sense of Lazear and Rosen [9] , Carmichael [10] , and Prendergast [11] . The problem of both approaches is that they could not model a clear manager-subordinate structure. Such a structure is a main element of hierarchies in firms [12] [13] . Another approach to model hierarchies might be games with an undirected graph/network on the set of players [3] -[5] . The problem is: all players are symmetrical in the graph; all players are in one level. The paper by van den Brink [14] uses a directed graph/permission structure on the set of players to analyze the effects of hierarchies on players’ payoffs. The basic idea is that a player needs approval from all predecessors. The approach was outlined in Gilles, Owen, and van den Brink [15] . The axiomatization is carried out by van den Brink and Gilles [16] .
In the modeling of van den Brink [14] , single dominance relationships, i.e. the influence of a predecessor on the direct successors, are equally strong. It is, however, quite a plausible assumption that the relations among the players can have different levels of strength (e.g. they account for different leadership styles). This possibility is especially necessary when mapping corporate hierarchies. With this in mind, Casajus, Hiller and Wiese [1] [2] introduce the  value. The authors use a weighted directed graph to model hierarchies. The basic idea for the
value. The authors use a weighted directed graph to model hierarchies. The basic idea for the 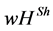 value includes two elements. In order to create the output, all players work symmetrically together. As a first step, the result generated is distributed to the players according to the Shapley value [17] . In a second step, the weighted hierarchy reallocates a certain fraction of these payoffs. A player
value includes two elements. In order to create the output, all players work symmetrically together. As a first step, the result generated is distributed to the players according to the Shapley value [17] . In a second step, the weighted hierarchy reallocates a certain fraction of these payoffs. A player  on the lowest hierarchical level gives the fraction
on the lowest hierarchical level gives the fraction  from his Shapley payoff to his direct predecessor
from his Shapley payoff to his direct predecessor  Player
Player 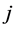 gives the fraction
gives the fraction  from all (gross) payoffs he receives (his Shapley payoff and the fractions from his successors) to his direct predecessor, etc. The weighted hierarchy has only allocation effects.
from all (gross) payoffs he receives (his Shapley payoff and the fractions from his successors) to his direct predecessor, etc. The weighted hierarchy has only allocation effects.
This is our starting point. We modify the 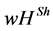 value in order to model the coordinating tasks of hierarchies. Within the framework of cooperative game theory, this is a new development starting from the papers done by Gilles, Owen, and van den Brink [15] , van den Brink and Gilles [16] , van den Brink [19] , and van den Brink [14] .
value in order to model the coordinating tasks of hierarchies. Within the framework of cooperative game theory, this is a new development starting from the papers done by Gilles, Owen, and van den Brink [15] , van den Brink and Gilles [16] , van den Brink [19] , and van den Brink [14] .
The paper is outlined as follows. In Section 3, we generalize the  value. Now the players do not work symmetrically together in order to create the output (first step). The problem of coordination of players is taken into account. The player who coordinates the other players is honored, if the coordination yields cooperation benefits. This approach is based on Hiller [18] . Section 4 concludes the paper. The paper starts with some preliminaries.
value. Now the players do not work symmetrically together in order to create the output (first step). The problem of coordination of players is taken into account. The player who coordinates the other players is honored, if the coordination yields cooperation benefits. This approach is based on Hiller [18] . Section 4 concludes the paper. The paper starts with some preliminaries.
2. Preliminaries
A TU game is a pair 
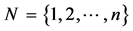 is the set of players. The coalitional function
is the set of players. The coalitional function 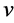 assigns every subset
assigns every subset  of
of  a certain worth
a certain worth 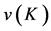 reflecting the economic abilities of
reflecting the economic abilities of  i.e.
i.e.  such that
such that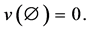 A game
A game  is called symmetric if a function
is called symmetric if a function  exists such that
exists such that  for all nonempty sets
for all nonempty sets , where
, where  denotes the cardinality of
denotes the cardinality of  A symmetric game is called monotone if
A symmetric game is called monotone if  for all
for all 

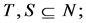 is increasing.
is increasing.
A TU value is an operator  that assigns pay off vectors to all games
that assigns pay off vectors to all games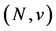 . One important value is the Shapley value. In order to calculate the players’ payoffs, rank orders
. One important value is the Shapley value. In order to calculate the players’ payoffs, rank orders  on
on  are used. They are written as
are used. They are written as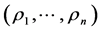 where
where  is the first player in the order,
is the first player in the order,  the second player etc. The set of the orders is denoted by
the second player etc. The set of the orders is denoted by ;
; 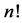 rank order sexist. The set of players before
rank order sexist. The set of players before  in rank order
in rank order 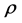 and player
and player  is called
is called  Thus, given a player
Thus, given a player  and a rank order
and a rank order , the marginal contribution of
, the marginal contribution of  is defined by
is defined by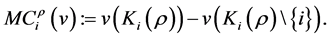 The Shapley value is the average of the marginal contributions taken over all rank orders of the players [17] :
The Shapley value is the average of the marginal contributions taken over all rank orders of the players [17] :
 (1)
(1)
In this note, we use one example to demonstrate the calculations.
Example 1 We assume a game with  and
and
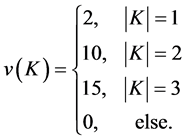 (2)
(2)
This game is symmetric and monotone. The  are calculated by:
are calculated by:
 (3)
(3)
As in Gilles, Owen, and van den Brink [15] , van den Brink and Gilles [16] , van den Brink [19] , van den Brink [14] , and Casajus, Hiller and Wiese [1] [2] , the permission structure is a mapping  It maps to each player
It maps to each player  those players that are direct successors of
those players that are direct successors of .
.  can be interpreted as directed graph [20] .
can be interpreted as directed graph [20] .  identifies the direct successors of
identifies the direct successors of  with
with  The players in
The players in  are called direct predecessors of
are called direct predecessors of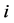 ;
; 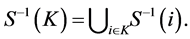
As usual in the literature, it is assumed that the hierarchy has a tree structure [21] [22] . These structures satisfy two conditions:
there is one player , such that
, such that  and
and 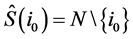 and
and
for every player 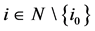 we have
we have .
.
In a tree structure, a path 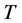 in
in  from
from  to
to  is a sequence of players
is a sequence of players  with
with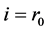 ,
,  and
and 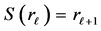 for all
for all . A path can be interpreted as a chain of commands between
. A path can be interpreted as a chain of commands between  and
and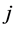 , whereby
, whereby  is a predecessor of
is a predecessor of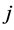 . The set of successors of
. The set of successors of  is denoted by
is denoted by . Analogously, we denote the set of
. Analogously, we denote the set of ’s predecessors by
’s predecessors by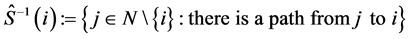 .
.
Beyond this hierarchy , weighted relations between players are considered. The vector
, weighted relations between players are considered. The vector  maps to every player
maps to every player 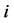 a weight
a weight ,
,  For
For  we have
we have  If a vector maps all players the same weight
If a vector maps all players the same weight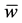 , except
, except  i.e.
i.e.  for all
for all 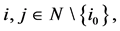 we also denote the vector by
we also denote the vector by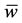 . With
. With  we denote a vector that maps to all
we denote a vector that maps to all  the weight zero,
the weight zero,  The players
The players 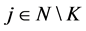 retain their initial weights,
retain their initial weights,  To simplify your notation, we write
To simplify your notation, we write  instead of
instead of .
.
A weighted hierarchical game is a tuple  A weighted hierarchical value is an operator
A weighted hierarchical value is an operator  The
The  value is one weighted hierarchical value. All players
value is one weighted hierarchical value. All players  with
with  respectively all players in the path
respectively all players in the path , get a fraction of
, get a fraction of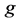 ’s Shapley payoff. Any player
’s Shapley payoff. Any player  gets from
gets from ’s Shapley payoff the fraction [1] [2] :
’s Shapley payoff the fraction [1] [2] :
 (4)
(4)
With this formula, the wH-payoff of player 
 is determined by [1] [2] :
is determined by [1] [2] :
 (5)
(5)
Example 2 In addition to example 1, we assume 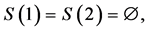
 and
and  Figure 1 illustrates the weighted hierarchy. For the players’
Figure 1 illustrates the weighted hierarchy. For the players’  payoffs, we have:
payoffs, we have:
 (6)
(6)
Casajus, Hiller and Wiese [1] [2] present eight axioms for the axiomatization of the  value. They can be categorized into two groups. The first four axioms—additivity (A), efficiency (E), weak symmetry (WS), weak null player (WN)—are modified Shapley axioms. They ensure that the Shapley payoffs results if
value. They can be categorized into two groups. The first four axioms—additivity (A), efficiency (E), weak symmetry (WS), weak null player (WN)—are modified Shapley axioms. They ensure that the Shapley payoffs results if  The last four axioms—gross net (GN), splitting (SP), isolation (IS), independency (ID)—control the reallocation from the bottom to the top of the hierarchy.
The last four axioms—gross net (GN), splitting (SP), isolation (IS), independency (ID)—control the reallocation from the bottom to the top of the hierarchy.
Axiom 3 (A) For all coalitional functions  and
and ,
,
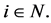
 (7)
(7)
A players’ payoff in the game  should be the sum of the payoffs he achieved in two separate games
should be the sum of the payoffs he achieved in two separate games  and
and 
Axiom 4 (E) It holds
 (8)
(8)
The worth  is distributed among the players.
is distributed among the players.
Definition 5 (S) Players  are called symmetric, if
are called symmetric, if  for all
for all 

I.e., both players  and
and  have the same marginal contributions to coalitions that do not contain them.
have the same marginal contributions to coalitions that do not contain them.
Axiom 6 (WS) If  are symmetric then
are symmetric then
 (9)
(9)
This axiom says that symmetric players get the same payoffs if all weights are zero.
Definition 7 (N) Player  is a null player, if
is a null player, if  for all
for all 
Axiom 8 (WN) If 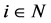 is a null player then
is a null player then
If all weights are zero, a null player gets the payoff zero.
Axiom 9 (GN) For the relation between gross and net payoffs, the equation
 (10)
(10)
holds.
The gross payoff  is the value that
is the value that  would receive if he did not have to pay anything to his direct predecessor. If this value is multiplied with
would receive if he did not have to pay anything to his direct predecessor. If this value is multiplied with , the net pay off results.
, the net pay off results.
Axiom 10 (SP) For the relation between player ’s pay off and player
’s pay off and player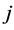 ’s payoff,
’s payoff,  , the following equation holds:
, the following equation holds:
 (11)
(11)
This axiom says that reducing the weight between  and
and  to zero (
to zero (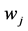 is changed to zero), reduces the gross payoff of player
is changed to zero), reduces the gross payoff of player  (left-hand side of equation) in the same way as it raises the payoff of player
(left-hand side of equation) in the same way as it raises the payoff of player  (right-hand side).
(right-hand side).
Axiom 11 (IS) For any player  holds:
holds:
 (12)
(12)
This axioms states that player  get the same payoff in two cases. In the first case, his weight is zero and the weights of his direct successors are zero too. In the second case, all players’ weights are zero.
get the same payoff in two cases. In the first case, his weight is zero and the weights of his direct successors are zero too. In the second case, all players’ weights are zero.
Axiom 12 (ID) If a player participates in two weighted hierachical games  and
and  with
with  for all
for all  then
then
 (13)
(13)
The games 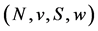 and
and  have the same set of players
have the same set of players , the same coalitional function
, the same coalitional function 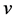 and the same hierarchy
and the same hierarchy 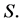 Further, the weight of
Further, the weight of  and the weights of all players
and the weights of all players  are the same in both games. The axiom states that
are the same in both games. The axiom states that  s payoff should be the same in both games.
s payoff should be the same in both games.
Now we will introduce some preliminaries for CO games (for a literature review on CO games see Slikker and van den Nouweland [23] ). This games account for coordination tasks of managers in firms. The set of possible pair wise links between players is called  whereat
whereat  and
and  respectively (or
respectively (or 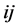 and
and  respectively) is the direct link between
respectively) is the direct link between 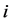 and
and . A cooperation structure on
. A cooperation structure on  is a graph
is a graph  with
with  A CO game
A CO game 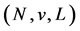 is a game
is a game  together with a cooperation structure
together with a cooperation structure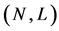 . A CO value is an operator
. A CO value is an operator  that assigns payoff vectors to all CO games. The most popular CO values are the Myerson value [3] , the position value [4] , and the average tree solution [5] . From
that assigns payoff vectors to all CO games. The most popular CO values are the Myerson value [3] , the position value [4] , and the average tree solution [5] . From 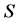 we construct
we construct  in the following way:
in the following way:  for all
for all  The tree structure is inherited from
The tree structure is inherited from  to
to  Hence, we have a CO game
Hence, we have a CO game 
Example 13 In our example, we have 
We will exemplify the CO generalization of the  value with the Myerson value. To calculate the Myerson payoffs, we need some more preliminaries. The graph partitions the set of players into components
value with the Myerson value. To calculate the Myerson payoffs, we need some more preliminaries. The graph partitions the set of players into components  This partition is denoted by
This partition is denoted by  Connected (directly or indirectly) players are in one component. Each player is in one component;
Connected (directly or indirectly) players are in one component. Each player is in one component; 


 denotes the component containing player
denotes the component containing player . Now, we can introduce the restricted coalitional function
. Now, we can introduce the restricted coalitional function  [3] :
[3] :
 (14)
(14)
The worth of a coalition  is the sum of the worth of its components. In the case of
is the sum of the worth of its components. In the case of  we have
we have for
for  The Myerson payoff of player
The Myerson payoff of player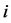 is determined by:
is determined by:
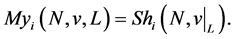 (15)
(15)
Example 14 In our example we have
 (16)
(16)
Hence, we obtain:
 (17)
(17)
Since player 3 coordinates the other players, he gets a higher payoff.
3. Generalization for CO Games
In this section we generalize the  value for CO games. First, we will introduce an axiom that is used to simplify the original axiomatization [18] :
value for CO games. First, we will introduce an axiom that is used to simplify the original axiomatization [18] :
Axiom 15 (zero weights invariance L, ZWIL) If  then
then  for all
for all 
This axiom says that the players get the payoff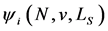 , if all weights are zero.
, if all weights are zero.  could be any efficient CO value. Using axiom ZWIL, we have Corollary 16 The
could be any efficient CO value. Using axiom ZWIL, we have Corollary 16 The  value is the unique weighted hierarchical value satisfying GN, SP, IS, ID, and ZWIL.
value is the unique weighted hierarchical value satisfying GN, SP, IS, ID, and ZWIL.
The formula to calculate the  payoff of player
payoff of player  is:
is:
 (18)
(18)
Hence it is now possible to model coordinating tasks within the  framework.
framework.
Using the  value for
value for , we get the
, we get the  payoffs:
payoffs:
 (19)
(19)
For our example, we obtain:
Example 17 In our example, we get the following  payoffs:
payoffs:
 (20)
(20)
For our example, Table 1 shows the players’ payoffs for the 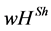 value and the
value and the 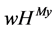 value. It is easy to see that the
value. It is easy to see that the  value rewards player
value rewards player  since he coordinates players 1 and 2.
since he coordinates players 1 and 2.
4. Conclusion
In this paper, we generalized the 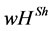 value for efficient CO values. The new value
value for efficient CO values. The new value  takes into account the problem of coordination of players—one main task for managers in firms. Hence, the
takes into account the problem of coordination of players—one main task for managers in firms. Hence, the  approach is another step in modelling firms and hierarchies. In the first step, the worth
approach is another step in modelling firms and hierarchies. In the first step, the worth  is divided among the players with respect to their productivity and their coordination tasks. In the second step, the weighted hierarchy reallocates a certain fraction of these payoffs. We hope that this value is an appropriate value for analyzing hierarchies in firms.
is divided among the players with respect to their productivity and their coordination tasks. In the second step, the weighted hierarchy reallocates a certain fraction of these payoffs. We hope that this value is an appropriate value for analyzing hierarchies in firms.