1. Introduction
This paper recalls the well-known property of different functions represented by the curves with sigmoidal shape (S-shape) [1] , involved with inflection (inf) point. An inflection point is the point on 2D plane where the curvature of the curve changes direction. The S-shape is characteristic, among others, for potentiometric titration curves [2] . Different methods of equivalence (eq) point determination are based on location of the inflection point on the curves pH = pH(V) or E = E(V), where E—potential, V—volume of titrant added. The inflection points are registered also in different physicochemical studies.
Generalizing, we refer to a monotonic function y = y(x). The inflection point (xinf, yinf) corresponds to maximal slope , where
, where
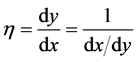 (1)
(1)
Applying the relation
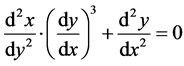 (2)
(2)
at the inflection point on the curve y = y(x) we have
 (3)
(3)
and then at dy/dx ¹ 0 we get
 (4)
(4)
It means that the maximal slope is equivalent with the relation (4) valid for the inverse function x = x(y). This property is important for pH titration curves; namely, the functions V = V(pH) assume relatively simple form [3] .
In this paper, we refer to a simple acid-base titration (y = pH, x = V), and to the relationship s = s(pH) for surface tension (y = s, x = pH).
2. Relation between Equivalence and Inflection Points in pH Titration
The main task of titration made for analytical purposes is the estimation of the equivalence volume (Veq). Let us consider the simplest case of titration of V0 mL of C0 mol/L HCl as titrand (D) with V mL of C mol/L NaOH as titrant (T). At V = Veq, the fraction titrated
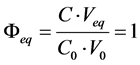 (5)
(5)
i.e., CVeq = C0V0. In this D+T system, the titration curve V = V(pH) has the form
 (6)
(6)
where
 (7)
(7)
To facilitate the calculations, it is advisable to rewrite (6) into the form
 (8)
(8)
From (5) and (6) we get
 (9)
(9)
From (8)
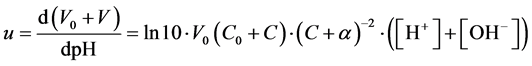
 (10)
(10)
Setting d2V/dpH2 = 0 and writing , from (10) we get, by turns,
, from (10) we get, by turns,
 (11)
(11)
From (11) we obtain for z = zinf
 (12)
(12)
and then for V = Vinf [3] [4]
 (13)
(13)
Analogous result can be obtained for titration of V0 mL of C0 mol/L NaCl with V mL AgNO3 [5] . Denoting [Ag+][Cl–] = Kso we get (13), where [5]
 (14)
(14)
At pKso = 9.75 for AgCl, V0 = 100 mL, C0 = 10–4 and C = 10–3, we get Veq – Vinf = 0.16 mL.
3. A Comment to Szyszkowski Formula
Many physicochemical processes are graphically represented by the curves with the sigmoidal shape. In this section, we refer to the function s = s(pH) obtained on the basis of Szyszkowski’s empirical formula [6]
 (15)
(15)
expressing the relationship between surface tension s and concentration [HL] of uncharged form HL of an aliphatic fatty acid as a surfactant in aqueous media; s0—surface tension of pure water, a, b—constants.
Denoting  and
and
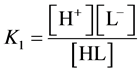
we get, by turns:

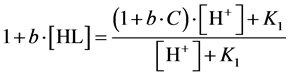
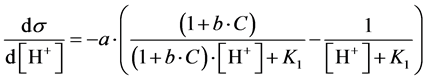


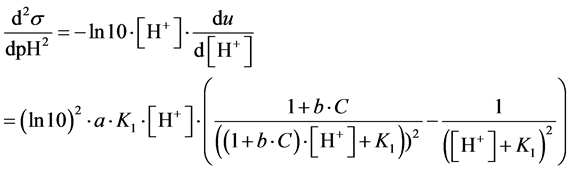 (16)
(16)
Putting d2s/dpH2 = 0, from Equation (16) we get [H+]∙(1 + b∙C)1/2 = K1, and then
 (17)
(17)
From Equation (17) it results that the abscissa (pHinf) corresponding to inflection point does not overlap with pK1 value for HL.