Keywords:Order Statistics; Semimartingales; Local Times; Arbitrage
1. Introduction
The theory of asset pricing and its fundamental theorem were initiated in the Arrow-Debreu model, the Black and Scholes formula, and the Cox and Ross model. They have now been formalized in a general framework by Harrison and Kreps [1], Harrison and Pliska [2], and Kreps [3] according to the no arbitrage principle. In the classical setting, the market is assumed to be frictionless i.e. a no arbitrage dynamic price process is a martingale under a probability measure equivalent to the reference probability measure.
However, real financial markets are not frictionless, and so an important literature on pricing under transaction costs and liquidity risk has appeared. See [4,]">5] and references therein. In these papers the bid-ask spreads are explained by transaction costs. Jouini and Kallal in []">5] in an axiomatic approach in continuous time assigned to financial assets a dynamic ask price process (respectively, a dynamic bid price process). They proved that the absence of arbitrage opportunities is equivalent to the existence of a frictionless arbitrage-free process lying between the bid and the ask processes, i.e., a process which could be transformed into a martingale under a well-chosen probability measure. The bid-ask spread in this setting can be interpreted as transaction costs or as the result of entering buy and sell orders.
Taking into account both transaction costs and liquidity risk, Bion-Nadal in [4] changed the assumption of sublinearity of ask price (respectively, superlinearity of bid price) made in []">5] to that of convexity (respectively, concavity) of the ask (respectively, bid) price. This assumption combined with the time-consistency property for dynamic prices allowed her to generalize the result of Jouini and Kallal []">5]. She proved that the “no free lunch” condition for a time-consistent dynamic pricing procedure [TCPP] is equivalent to the existence of an equivalent probability measure 
that transforms a process between the bid and ask processes of any financial instrument into a martingale. See also Cherny [6] regarding the characterization of non-existence of arbitrage opportunities for stock prices constructed from bid and ask processes.
In recent years, a pricing theory has also appeared taking inspiration from the theory of risk measures. First to investigate in a static setting were Carr, Geman, and Madan [7] and Föllmer and Schied [8]. The point of view of pricing via risk measures was also considered in a dynamic way using backward stochastic differential equations [BSDE] by El Karoui and Quenez [9], El Karoui, Peng, and Quenez [10], and Peng [11,12]. This theory soon became a useful tool for formulating many problems in mathematical finance, in particular for the study of pricing and hedging contingent claims [10]. Moreover, the BSDE point of view gave a simple formulation of more general recursive utilities and their properties, as initiated by Duffie and Epstein (1992) in their [stochastic differential] formulation of recursive utility [10].
In the past, in real financial markets, the load of providing liquidity was given to market makers, specialists, and brokers, who trade only when they expect to make profits. Such profits are the price that investors and other traders pay, in order to execute their orders when they want to trade. To ensure steady trading, the market makers sell to buyers and buy from sellers, and get compensated by the so-called bid-ask spread. The most common price for referencing stocks is the last trade price. At any given moment, in a sufficiently liquid market there is a best or highest “bid” price, from someone who wants to buy the stock and there is a best or lowest “ask” price, from someone who wants to sell the stock. The best bid price 
and best ask (or best offer) price 
are the highest buying price and the lowest selling price at any time 
of trading.
In the present work, we consider models of financial markets in which all parties involved (buyers, sellers) find incentives to participate. Our framework is different from the existing approach (see [4,]">5] and references therein) where the authors assume some properties (sublinearity, convexity, etc.) on the ask (respectively, bid) price function in order to define a dynamic ask (respectively, bid). Rather, we assume that the different bid and ask prices are given. Then the question we address is how to model the “best bid” (respectively, the “best ask”) price process with the intention to obtain the stock price dynamics.
The assumption that the bid and ask processes are described by (continuous) semimartingales in our special setting entails that the stock price admits arbitrage opportunities. Further, it turns out that the price process possesses the Markov property, if the bid and ask are Brownian motion or Ornstein-Uhlenbeck type, or more generally Feller processes. Note that our results are obtained without assuming arbitrage opportunities.
This paper is also related with [13] where the authors explore market situations where a large trader causes the existence of arbitrage opportunities for small traders in complete markets. The arbitrage opportunities considered are “hidden” which means that they are almost not observable to the small traders, or to scientists studying markets because they occur on time sets of Lebesgue measure zero.
The paper is organized as follows: Section 2 presents the model. Section 3 studies the Markovian property of the processes, while Sections 4 and 5 are devoted to the study of completeness, arbitrage and (insider) hedging on a market driven by such processes.
2. The Model
Let 
(where 
denotes transpose) be a n-dimensional standard Brownian motion on a filtered probability space
.
Suppose bid and ask price processes
, which are modeled by continuous semimartingales
(1)
Here we consider the following model for bid and ask prices. See Figure 1.
The evolution of the stock price process 
is based on
. Denote by 
the Best Bid and Ask(t) the Best Ask at time t. Then 
is the lowest price that a day trader seller is willing to accept for a stock at that time and Ask(t) is the highest price that a day trader buyer is willing to pay for that stock at any particular point in time. Let us define the processes 
and
. Further set
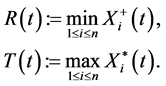
where we use the convention that 
and
. Then 
and 
can be modeled as
(2)
and
(3)
Given 
and
, the market makers will agree on a stock price within the Bid/Ask spread, that is
(4)
where 
is a stochastic process such that 
One could choose e.g., 
for a function 
or 
for a function
.
For convenience, we will from now on assume that
, that is
(5)
3. Markovian Property of Processes R, T and S
For convenience, let us briefly discuss the Markovian property of the processes 
and
in some particular cases. The two cases considered here are the cases when the process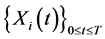 
are Brownian motions or Ornstein-Uhlenbeck processes. Let us first have on the definition of semimartingales rank processes.
Definition 3.1 Let 
be continuous semimartingales. For
, the k-th rank process of 
is defined by
(6)
where 
and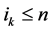
.
Note that, according to Definition 3.1, for
,
(7)
so that at any given time, the values of the rank processes represent the values of the original processes arranged in descending order (i.e. the (reverse) order statistics).
Using Definition 3.1, we get
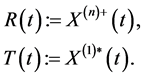(8)
3.1. The Brownian Motion Case
Here we assume that the processes 
are independent Brownian motions.
Proposition 3.2 The process 
possesses the Markov property with respect to the filtration
.
Proof. Let 
be a one-dimensional Brownian motion. We first prove that 
is a Markov process. Define the process
Then 
is a two dimensional Feller process.
Let
. One observes that 
is a continuous and open map. Thus is follows from [14] (Remark 1, p. 327) that 
is a Feller process, too.
The latter argument also applies to the n-dimensional case, that is 
is a Feller process. Since
is a continuous and open map we conclude that 
is a Feller process.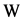 
Proposition 3.3 The process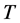 
possesses Markov property with respect to the filtration
.
Proof. See the proof of Proposition 3.2.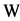 
Corollary 3.4 The process 
possesses Markov property with respect to the filtration
.
Proof. The process 
defined by 
for all 
is a Markov process as sum of two Markov processes. 
3.2. The Ornstein-Uhlenbeck Case
Here we assume that the process 
is an n-dimensional Ornstein-Uhlenbeck, that is
(9)
where 
and 
are parameters. It is clear that an Ornstein-Uhlenbeck process is a Feller process. So we obtain Proposition 3.5 The process 
and 
defined by (8) and (5) possess Markov property.
Proof. The conclusion follows from the proof of Proposition 3.2.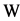 
Remark 3.6 Using continuous and open transformations of Markov processes, the above results can be generalized to the case, when the bid and ask processes are Feller processes. See [14].
4. Further Properties of S(t)
In this Section, we want to use the semimartingale decomposition of our price process 
to analyze completeness and arbitrage on market driven by such a process.
We need the following result. See [15] (Proposition 4.1.11). See also [16] for the continuous semimartingales case and [17] for general semimartingales.
Theorem 4.1 Let 
be continuous semimartingales of the form (1). For 
let 
be any predictable process with the property:
(10)
Then the k-th rank processes
, are semimartingales and we have:
(11)
where 
is the local time of the semimartingale 
at zero, defined by
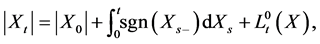
where
.
For completeness, we give the proof of the proposition.
Proof. We find that
(12)
where we used the property
. It follows,
We note the fact
(13)
We now use the following formula:
(14)
which is valid for non-negative semimartingales
. See, e.g., [15,18]
Then, by applying (14) to
, (12) becomes:
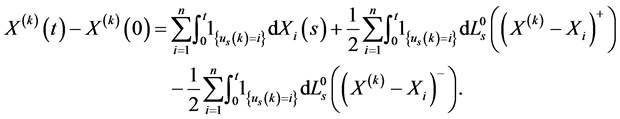
Then proof is completed.
4.1. The Brownian Motion Case
If 
are 
independent Brownian motions, the evolution of 
and 
follows from Theorem 4.1.
Corollary 4.2 Let the processes 
and 
be given by Equation (8). Then 
and 
and we have:
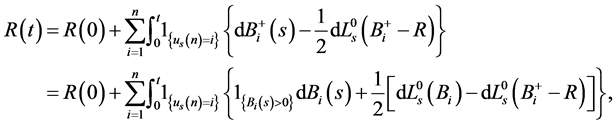(15)
and
(16)
We can rewrite 
and 
as follows:
where 
are continuous local martingales and 
are continuous processes of locally bounded variation given by:
(17)
(18)
(19)
(20)
The following corollary gives the semimartingale decomposition satisfied by the process
.
Corollary 4.3 Assume that the process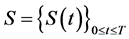 
is given by (5). Then one can write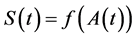 
where 
and
, and we have:
(21)
In order to price options with respect to
, one should ensure that 
does not admit arbitrage possibilities and the natural question which arises at this point is the following: Can we find an equivalent probability measure 
such that, 
is a 
-sigma martingale? Since the process 
is continuous, we can reformulate the question as: Can we find an equivalent probability measure 
such that, 
is a 
local martingale1?
We first give the following useful remark; See [19] (Theorem 1).
Remark 4.4 Let 
be a continuous semimartingale on a filtered probability space
. Let
. A necessary condition for the existence of an equivalent martingale measure is that
.
Consequence 4.5 Since local time is singular, we observe that the total variation of the bounded variation part in 21 cannot be absolutely continuous with respect to the quadratic variation of the martingale. It follows that, the set of equivalent martingale measures is empty, and thus, such a market contains arbitrage opportunities.
4.2. (In)complete Market with Hidden Arbitrage
In this Section, we consider a model with
, denoting a stochastic process modeling the price of a risky asset, and 
denotes the value of a risk free money market account. We assume a given filtered probability space
, where 
satisfies the “usual hypothesis”. In such a market, a trading strategy 
is self-financing if 
is predictable, 
is optional, and
(22)
for all
. For simplicity, we let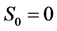 
and 
(thus the interest rate
), so that
, and (22) becomes
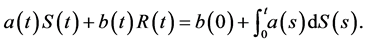
Definition 4.6 (See [13])
• We call a random variable 
a contingent claim. Further, a contingent claim 
is said to be 
-redundant if, for a probability measure
, there exists a self-financing strategy 
such that
(23)
where 
is the value of the portfolio.
• A market 
is 
-complete if every 
is 
-redundant.
Define the process 
as follows
(24)
Then the following theorem is immediate from [13] (Theorem 3.2).
Theorem 4.7 Suppose that there exists a unique probability measure 
equivalent to 
such that 
is a 
-local martingale. Then, the market 
is 
-complete.
Proof. Omitted.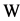 
Proposition 4.8 Suppose that
. Then, there exists no unique martingale measure 
such that 
is a 
-local martingale.
Proof. From (24), we observe that 
is a 
-martingale. Let us construct another equivalent martingale measure 
For this purpose, assume without loss of generality that 
and 
are given by
and
Now define the process 
as
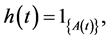
where
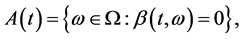
with
(25)
One finds that 
for all
. Let us define the equivalent measure 
with respect to a density process 
given by
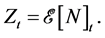
Here, 
denotes the Doléans-Dade exponential of the martingale 
defined by
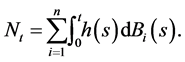
Then, it follows from the Girsanov-Meyer theorem (see [20]) that 
has a 
-semimartingale decomposition with a bounded variation part given by 
We have that
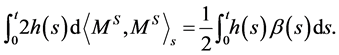
Since
, it follows that
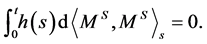
Thus 
is a 
-martingale. Since 
is also a martingale measure with
, the result follows. 
Remark 4.9 In the case 
(a single Bid/Ask), the market becomes complete since the process
, defined by Equation (25) in the proof is equal to
. Therefore the unique martingale measure is
.
We can then deduce the following theorem on our process
.
Theorem 4.10 Suppose that 
and 
are given by (21) and (24), respectively. Then
• For 
(a single Bid/Ask), the market 
is 
-complete and admits the arbitrage opportunity (26).
• For 
(more than a single Bid/Ask), the market 
is incomplete and arbitrage exists.
Proof. From Theorem 4.8, we know that the market is 
-complete for 
and incomplete for
. Let 
such that 
is a 
-local martingale. For
, let us construct an arbitrage strategy. Let
(26)
where 
denotes the 
by 
support of the (random) measure
; that is, for fixed 
it is the smallest closed set in 
such that 
does not charge its complement. (Compare with the proof of Proposition 4.8.) Let
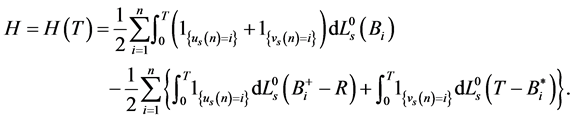
Assume without loss of generality that
. Then, by Theorem 4.7, there exists a self financing strategy 
such that 
However, from (26), we also have
Moreover, we have
, by construction of the process
.
Hence, 
which is an arbitrage opportunity.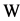 
Remark 4.11 We do not make the assumption that we are working in an arbitrage free market, rather, we define the notion of redundancy (see [13] Definition 2.1), which in some sense is equivalent to the notion of replication with the difference that, replication is on a arbitrage free setting.
5. Pricing and Insider Trading with Respect to S(t)
In this Section, we discuss a framework introduced in [21], which enables us pricing of contingent claims with respect to the price process 
of the previous sections. We even consider the case of insider trading, that is, the case of an investor, who has access to insider information. To this end, we need some notions.
We consider a market driven by the stock price process 
on a filtered probability space
. We assume that, the decisions of the trader are based on market information given by the filtration 
with 
for all 
being a fixed terminal time. In this context an insider strategy is represented by an 
-adapted process 
and we interpret all anticipating integrals as the forward integral; See, for e.g., [22,23] for more details. In such a market, a natural tool to describe the self-financing portfolio is the forward integral of an integrand process 
with respect to an integrator
denoted by
; See [23]. The following definitions and concepts are consistent with those given in [21].
Definition 5.1 A self-financing portfolio is a pair
, where 
is the initial value of the portfolio and 
is a 
-adapted and 
-forward integrable process specifying the number of shares of held in the portfolio. The market value process 
of such a portfolio at time
, is given by
(27)
while 
constitutes the number of shares of the less risky asset held.
5.1. 
-Martingales
Now, we briefly review the definition of 
-martingales which generalizes the concept of a martingale. We refer to [21] for more information about this notion. Throughout this Section, 
will be a real linear space of measurable processes indexed by 
with paths which are bounded on each compact interval of
.
Definition 5.2 A process 
is said to be a 
-martingale, if every 
in 
is 
-improperly forward integrable and
(28)
Definition 5.3 A process 
is said to be 
-semimartingale if it can be written as the sum of an 
-martingale 
and a bounded variation process
, with
.
• Remark 5.4
• Let 
be a continuous 
-martingale with 
belonging to
, then, the quadratic variation of 
exists improperly. In fact, if 
exists improperly, then one can show that 
exists improperly and
.
• Let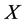 
a continuous square integrable martingale with respect to some filtration
. Suppose that every process in 
is the restriction to 
of a process 
which is 
-adapted. Moreover, suppose that its paths are left continuous with right limits and
. Then 
is an 
-martingale.
5.2. Completeness and Arbitrage: 
-Martingale Measures
The subsequent definitions and notions are from [21].
Definition 5.5 Let 
be a self-financing portfolio in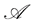
, which is 
-improperly forward integrable and 
its wealth process. Then 
is an 
-arbitrage if 
exists almost surely, 
and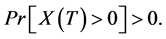 
Definition 5.6 If there is no 
-arbitrage, the market is said to be 
-arbitrage free.
Definition 5.7 A probability measure 
is called a 
-martingale measure if with respect to 
the process 
is an 
-martingale according to Definition 5.2.
We need need the following assumption. See [21].
Assumption 5.8 Suppose that for all 
in 
the following condition holds. Then 
is 
-improperly forward integrable and
(29)
The proof of the following proposition can be found in [21].
Proposition 5.9 Under Assumption 5.8, if there exists an 
-martingale measure
, the market is 
-arbitrage free.
Definition 5.10 A contingent claim is an 
-measurable random variable. Let 
be the set of all contingent claims the investor is interested in.
• Definition 5.11
• A contingent claim 
is called 
-attainable if there exists a self-financing trading portfolio 
with 
in
, which is 
-improperly forward integrable, and whose terminal portfolio value coincides with
, i.e.,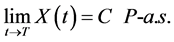 
Such a portfolio strategy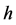 
is called a replicating or hedging portfolio for 
and 
is the replication price for
.
• A 
-arbitrage free market is called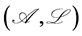 
-complete if every contingent claim in 
is attainable.
Assumption 5.12 For every 
-measurable random variable
, and 
in 
the process
, belongs to
.
Proposition 5.13 Suppose that the market is 
-arbitrage free, and that Assumption 5.8 holds. Then the replication price of an attainable contingent claim is unique.
Proof. Let 
be a given measure equivalent to
. For such a
, let 
be a set of all strategies (
- adapted) such that (28) in Definition 5.2 is satisfied. Then, it follows from Proposition 5.9 that the market 
in Section 4.2 is 
-arbitrage free. 
Next, we shall discuss attainability of claims in connection with a concrete set 
of trading strategies.
5.3. Hedging with Respect to S(t)
In this Section, we want to determine hedging strategies for a certain class of European options with respect to the price process 
of Section 4.2. Let us now assume that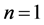 
(a single Bid/Ask). Then, the price process 
is the sum of a Wiener process and a continuous process with zero quadratic variation; moreoverwe have that
, where 
is given by (25). We can derive the following proposition which is similar to [21] (Proposition 5.29).
Proposition 5.14 Let 
be a function in 
of polynomial growth. Suppose that there exist
of class 
which is a solution of the following Cauchy problem
(30)
Set
Then 
is a self-financing portfolio replicating the contingent claim
.
In particular,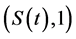 
is 
-complete, where 
is given by
and 
by all claims as stated in this Proposition.
Proof. The proof is a direct consequence of Itô’s Lemma for forward integrals. See [21] (Proposition 5.29).
6. Conclusion
In this paper, assuming that the dynamics of the bid and ask prices are given by Itô processes, we derive the stochastic differential equation satisfied by the “best bid” and the “best ask” from which we get the dynamic of the middle (stock) price. The evolution of the latter is given by a semimartingale, whose final variation part, is not absolute continuous with respect to the Lebesgue measure. We then show that, such a market admits a hidden arbitrage opportunity and compute the arbitrage strategy. We also discuss the notion of (insider) hedging in this market.
NOTES
1In fact since S is continuous and since all continuous sigma martingales are in fact local martingales, we only need to concern ourselves with local martingales