Keywords:p-Adic Numbers; Solvability of Equation; Congruence
1. Introduction
In the present time description of different structures in mathematics are studying over field of  -adic numbers. In particular,
-adic numbers. In particular,  -adic analysis is one of the intensive developing directions of modern mathematics. Numerous applications of
-adic analysis is one of the intensive developing directions of modern mathematics. Numerous applications of  -adic numbers have found their own reflection in the theory of
-adic numbers have found their own reflection in the theory of  -adic differential equations,
-adic differential equations,  -adic theory of probabilities,
-adic theory of probabilities,  -adic mathematical physics, algebras over
-adic mathematical physics, algebras over 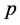 - adic numbers and others.
- adic numbers and others.
The field of  -adic numbers were introduced by German mathematician K. Hensel at the end of the 19th century [2]. The investigation of
-adic numbers were introduced by German mathematician K. Hensel at the end of the 19th century [2]. The investigation of  -adic numbers were motivated primarily by an attempt to bring the ideas and techniques of the power series into number theory. Their canonical representation is similar to expansion of analytical functions in power series, which is analogy between algebraic numbers and algebraic functions. There are several books devoted to study
-adic numbers were motivated primarily by an attempt to bring the ideas and techniques of the power series into number theory. Their canonical representation is similar to expansion of analytical functions in power series, which is analogy between algebraic numbers and algebraic functions. There are several books devoted to study  -adic numbers and
-adic numbers and  -adic analysis [3-6].
-adic analysis [3-6].
Classification of algebras in small dimensions plays important role for the studying of properties of varieties of algebras. It is known that the problem of classification of finite dimensional algebras involves a study on equations for structural constants, i.e. to the decision of some systems of the Equations in the corresponding field. Classifications of complex Leibniz algebras have been investigated in [7-10] and many other works. In similar complex case, the problem of classification in  -adic case is reduced to the solution of the Equations in the field. The classifications of Leibniz algebras over the field of
-adic case is reduced to the solution of the Equations in the field. The classifications of Leibniz algebras over the field of  -adic numbers have been obtained in [11-13].
-adic numbers have been obtained in [11-13].
In the field of complex numbers the fundamental Abel’s theorem about insolvability in radicals of general Equation of 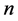 -th degree
-th degree  is well known. In this field square equation is solved by discriminant, for cubic Equation Cardano’s formulas were widely applied. In the field of
is well known. In this field square equation is solved by discriminant, for cubic Equation Cardano’s formulas were widely applied. In the field of  -adic numbers square equation does not always has a solution. Note that the criteria of solvability of the Equation
-adic numbers square equation does not always has a solution. Note that the criteria of solvability of the Equation  is given in [6,14,15] we can find the solvability criteria for the Equation
is given in [6,14,15] we can find the solvability criteria for the Equation  where
where 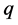 is an arbitrary natural number.
is an arbitrary natural number.
In this paper we consider  adic cubic equation
adic cubic equation  By replacing
By replacing  this equation become the so-called depressed cubic equation
this equation become the so-called depressed cubic equation
 (1)
(1)
The solvability criterion for the cubic equation  over
over  -adic numbers is different from the case
-adic numbers is different from the case  Note that solvability criteria for
Note that solvability criteria for  is obtained in [1]. The problem of finding a solvability criteria of the cubic equation for the case
is obtained in [1]. The problem of finding a solvability criteria of the cubic equation for the case  is complicated. This problem was partially solved in [16], namely, it is obtained solvability criteria of cubic equation with condition
is complicated. This problem was partially solved in [16], namely, it is obtained solvability criteria of cubic equation with condition .
.
In this paper we obtain solvability criteria of cubic equation for 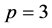 without any conditions. Moreover, the algorithm of finding the solutions of the equation
without any conditions. Moreover, the algorithm of finding the solutions of the equation  in
in  with coefficients from
with coefficients from  is provided.
is provided.
2. Preliminaries
Let  be a field of rational numbers. Every rational number
be a field of rational numbers. Every rational number  can be represented by the form
can be represented by the form
 , where
, where 
 is a positive integer,
is a positive integer,  and
and  is a fixed prime number. In
is a fixed prime number. In  a norm has been defined as follows:
a norm has been defined as follows:
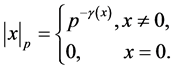
The norm  is called a
is called a 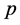 -adic norm of
-adic norm of  and it satisfies so called the strong triangle inequality. The completion of
and it satisfies so called the strong triangle inequality. The completion of  with respect to
with respect to  -adic norm defines the
-adic norm defines the  -adic field which is denoted by
-adic field which is denoted by  ([4,6]). It is well known that any
([4,6]). It is well known that any  -adic number
-adic number 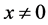 can be uniquely represented in the canonical form
can be uniquely represented in the canonical form

where  and
and  are integers,
are integers,  ,
,  ,
,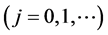 .
.  -Adic number
-Adic number  for which
for which , is called integer
, is called integer  -adic number, and the set of such numbers is denoted by
-adic number, and the set of such numbers is denoted by  Integer
Integer
 for which
for which  is called unit of
is called unit of  and their set is denoted by
and their set is denoted by .
.
For any numbers  and
and  it is known the following result.
it is known the following result.
Theorem 2.1 [3]. If  then a congruence
then a congruence  has one and only one solution.
has one and only one solution.
We also need the following Lemma.
Lemma 2.1 [14]. The following is true:
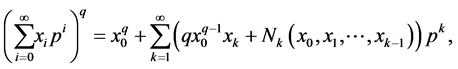
where ,
,  ,
,  and for
and for 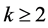

From Lemma 2.1 by  we have
we have
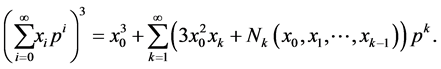
For  we put
we put

Also the following identity is true:
 (2)
(2)
3. The Main Result
In this paper we study the cubic Equation (1) over the field  -adic numbers, i.e.
-adic numbers, i.e. 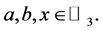
Put
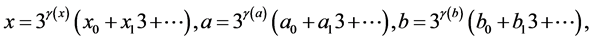
where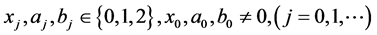 .
.
Since any  -adic number
-adic number  has a unique form
has a unique form  where
where  and
and  we will be limited to search a decision from
we will be limited to search a decision from  i.e.
i.e. .
.
Putting the canonical form of  and
and  in (1), we get
in (1), we get

By Lemma 2.1 and Equality (2), the Equation (1) becomes to the following form:
 (3)
(3)
Proposition 3.1 If one of the following conditions:

is fulfilled, then the Equation (1) has not a solution in 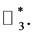
Proof. 1) Let  and
and  Multiplying Equation (3) by
Multiplying Equation (3) by  we get the following congruence
we get the following congruence 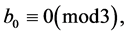 which is not correct. Consequently, Equation (1) has no solution in
which is not correct. Consequently, Equation (1) has no solution in 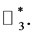
2) Let  and
and 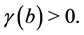 Then from (3) it follows a congruence
Then from (3) it follows a congruence  which has no a nonzero solution.Therefore, in
which has no a nonzero solution.Therefore, in 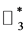 Equation (1) does not have a solution.
Equation (1) does not have a solution.
In other cases, we analogously get the congruences
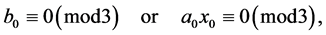
which are not hold. Therefore, in  there is no solution.■
there is no solution.■
From the Proposition 3.1 we have that the cubic equation may have a solution if one of the following four cases
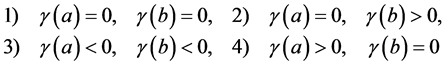
is hold.
In the following theorem we present an algorithm of finding of the Equation  for the first case.
for the first case.
Theorem 3.1 Let 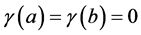 and
and  Then
Then  to be a solution of the Equation (1) in
to be a solution of the Equation (1) in  if and only if the congruences
if and only if the congruences
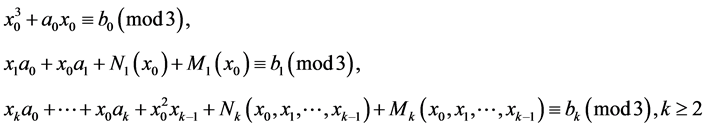
are fulfilled, where integers  are defined consequently from the following correlations
are defined consequently from the following correlations
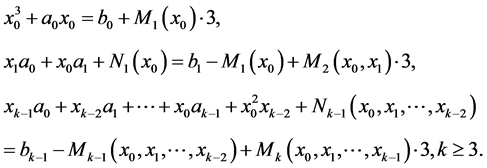
Proof. Let
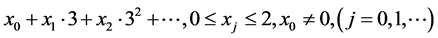
is a solution of Equation (1), then Equality (3) becomes
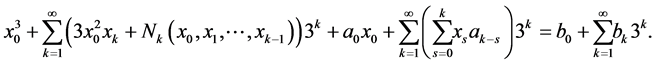
So we have
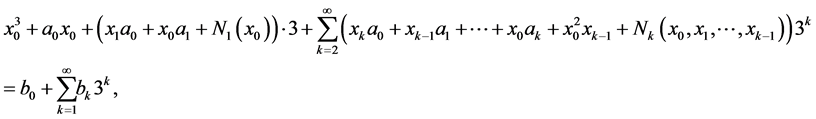
from which it follows the necessity in fulfilling the congruences of the theorem.
Now let  is satisfied the congruences of the theorem. Since
is satisfied the congruences of the theorem. Since  then by Theorem 2.1 it implies that these congruences have the solutions
then by Theorem 2.1 it implies that these congruences have the solutions 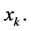
Then
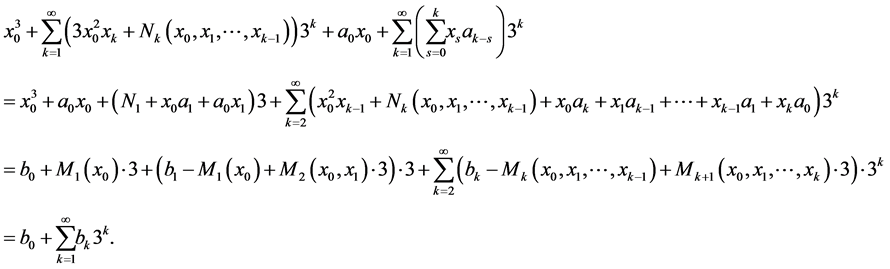
Therefore, we show that  is a solution of the Equation (1).■
is a solution of the Equation (1).■
Let us examine a case  and get necessary and sufficient conditions for a solution of Equation (1).
and get necessary and sufficient conditions for a solution of Equation (1).
Theorem 3.2 Let 
 and
and  Then
Then  to be a solution of Equation (1) in
to be a solution of Equation (1) in  if and only if the congruences
if and only if the congruences

are fulfilled, where integers  are defined consequently from the following correlations
are defined consequently from the following correlations
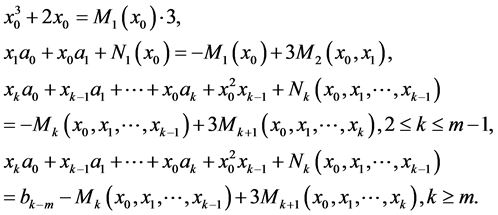
Proof. Let  is a solution of the Equation (1), then Equality (3) becomes
is a solution of the Equation (1), then Equality (3) becomes
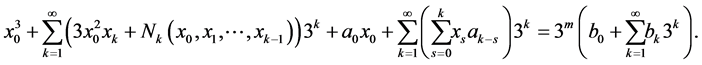
Therefore, we have
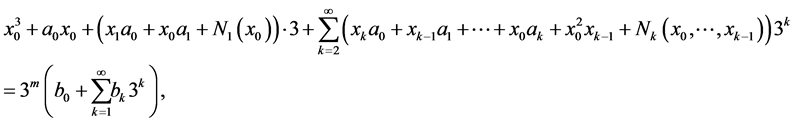
from which it follows the necessity in fulfilling the congruences of the theorem.
Now let  is satisfied the congruences of the theorem. Since
is satisfied the congruences of the theorem. Since  then by Theorem 2.1 there are solutions
then by Theorem 2.1 there are solutions  of the congruences.
of the congruences.
Putting element  to Equality (3), we have
to Equality (3), we have
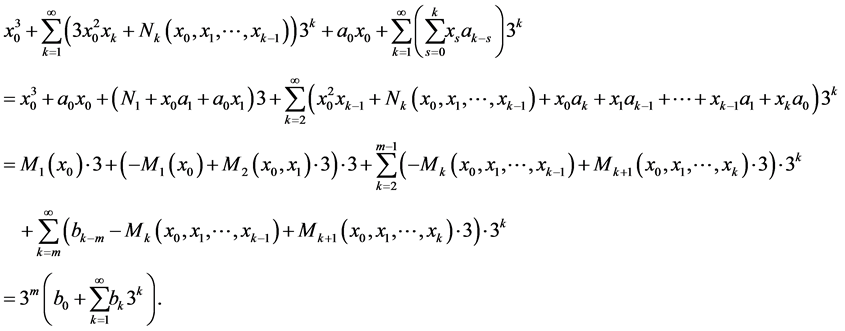
Therefore, we show that  is a solution of Equation (1).■
is a solution of Equation (1).■
The following theorem gives necessary and sufficient conditions for a solution of Equation (1) for the case  and
and 
Theorem 3.3 Let

Then  to be a solution of Equation (1) in
to be a solution of Equation (1) in  if and only if the next congruences
if and only if the next congruences
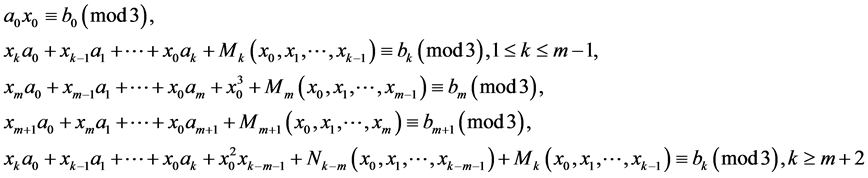
are fulfilled, where integers  are defined consequently from the equalities
are defined consequently from the equalities
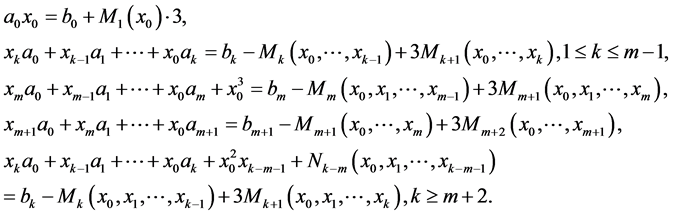
Proof. The proof of the Theorem can be obtained by similar way to the proofs of Theorems 3.1 and 3.2.■
Examining various cases of  and
and  we need to study only the case
we need to study only the case  and
and  Because of appearance of uncertainty of a solution, we divide this case to
Because of appearance of uncertainty of a solution, we divide this case to  and
and 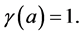
Theorem 3.4 Let 
 and
and 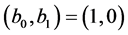 or
or  Then
Then  to be a solution of Equation (1) in
to be a solution of Equation (1) in  if and only if he next congruences
if and only if he next congruences
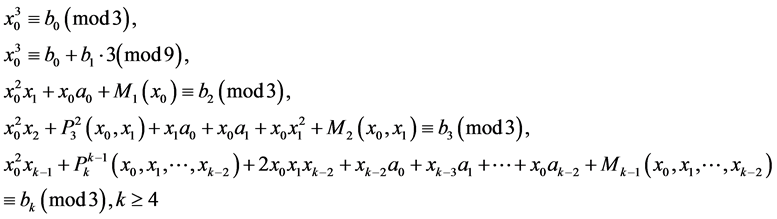
are fulfilled, where integers  are defined from the equalities
are defined from the equalities

Proof. Analogously to the proof of Theorem 3.1.■
Theorem 3.5 Let 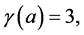
 and
and  or
or  Then
Then  to be a solution of the Equation (1) in
to be a solution of the Equation (1) in  if and only if he next congruences
if and only if he next congruences
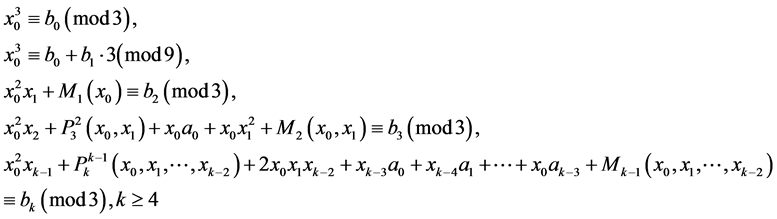
are fulfilled, where integers  are defined from the equalities
are defined from the equalities

Proof. Analogously to the proof of Theorem 3.1.■
Similarly to Theorem 3.4, it is proved the following Theorem 3.6 Let 
 and
and  or
or  Then
Then  to be a solution of the Equation (1) in
to be a solution of the Equation (1) in 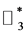 if and only if he next congruences
if and only if he next congruences

are fulfilled, where integers  are defined from the equalities
are defined from the equalities
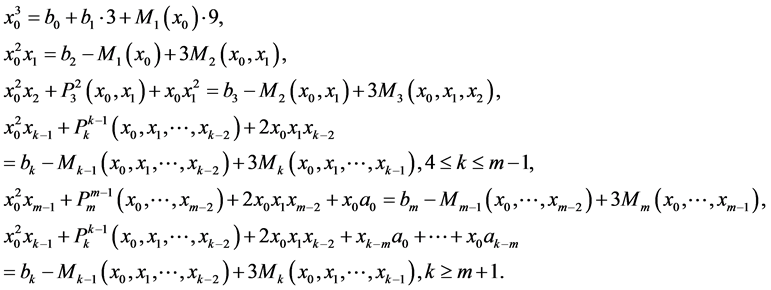
Now we consider Equality (3) with 
 Put
Put
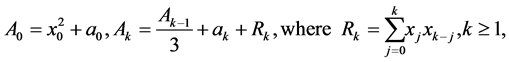
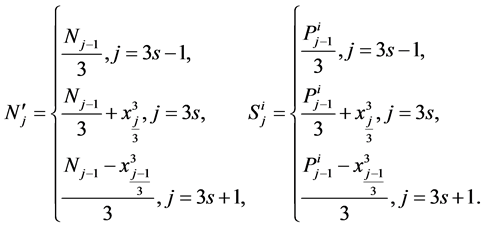
Theorem 3.7 Let 
 and
and  to be so that
to be so that  Then
Then  to be a solution of Equation (1) in
to be a solution of Equation (1) in  if and only if the congruences
if and only if the congruences

are faithfully, where 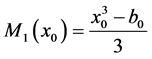 and integers
and integers  are defined from the equalities
are defined from the equalities
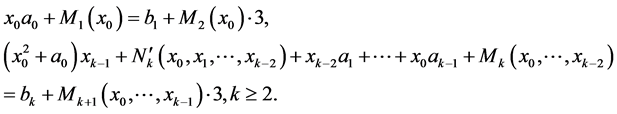
Proof. Let the congruences  has a solution
has a solution  Then denote by
Then denote by
 the number satisfying the equality
the number satisfying the equality 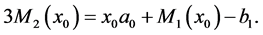
Using Theorem 2.1, we have existence of solutions  of the congruences
of the congruences
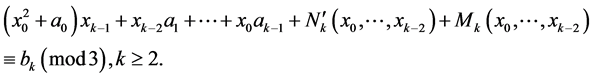
The next chain of equalities
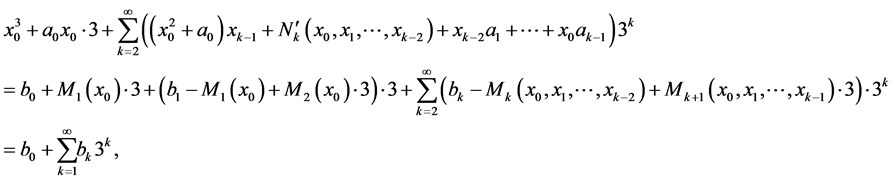
shows that 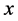 is a solution of Equation (1).■
is a solution of Equation (1).■
From the proof of Theorem 3.7, it is easy to see that if  then we have the following congruences and appropriate equalities a)
then we have the following congruences and appropriate equalities a)  i.e.
i.e. 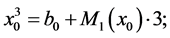
b)  then
then 
c) 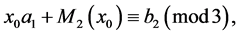 then
then
 (4)
(4)
d)  it follows that
it follows that

Since  then the congruence d) can be written in the form
then the congruence d) can be written in the form

and so we have
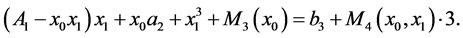
If for any natural number  we have
we have  then we could establish the criteria of solvability for Equation (1). However, if there exists
then we could establish the criteria of solvability for Equation (1). However, if there exists , such that
, such that  then the criteria of solvability can be found, and therefore, we need the following Lemma 3.1 Let
then the criteria of solvability can be found, and therefore, we need the following Lemma 3.1 Let 
 and
and  to be so that
to be so that 
 for some fixed
for some fixed . If
. If  be a solution of Equation (1), then it is true the following system of the congruences
be a solution of Equation (1), then it is true the following system of the congruences
 (5)
(5)
where  and integers
and integers  are defined from the equalities
are defined from the equalities
 (6)
(6)
Proof. We will prove Theorem by induction. Let 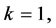 i.e.
i.e.
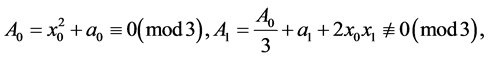
then the system of the congruences (4) are true. Note that 
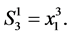
From (3) it is easy to get
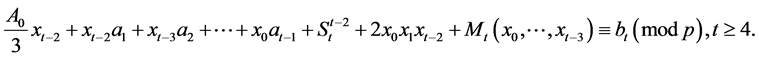
Therefore,
 (7)
(7)
where
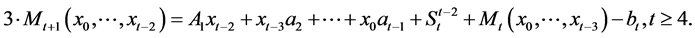
Obviously, the statement of Lemma is true for  i.e. for
i.e. for 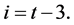
Let  i.e.
i.e.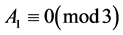
 ,
,  then from the equalities (7) it follows that the following congruences are be added to the system (4):
then from the equalities (7) it follows that the following congruences are be added to the system (4):
e)  it follows
it follows
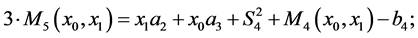
f)  it follows
it follows
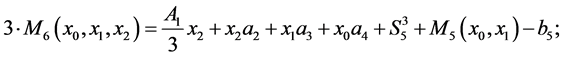

where  and
and  are defined by equalities
are defined by equalities
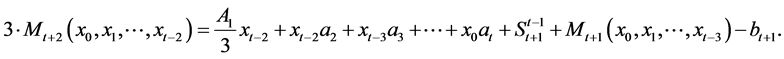
Since 


 we denote by
we denote by  and have e)
and have e) 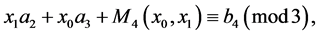
f) 
h) 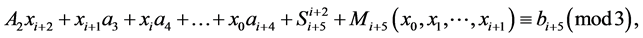 where
where

So we showed that the statement of Lemma is true for 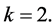
Let the system of congruences (5) and (6) is true for  Since
Since 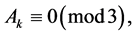 then from the congruences
then from the congruences

we derive

It is easy to check that
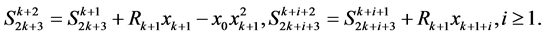
By these correlations we deduce
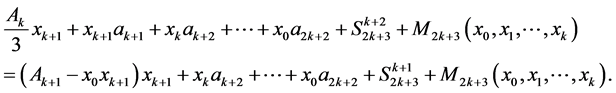
For  we get
we get
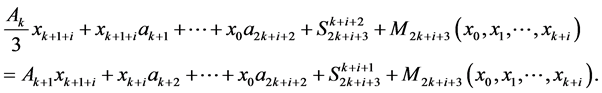
Consequently, we have


So we established that the system of congruences (5)-(6) is true for ■
■
Using the Lemma 3.1 we obtain the following Theorems.
Theorem 3.8 Let 
 and
and  to be such that
to be such that 
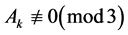 for some fixed
for some fixed . Then
. Then  to be a solution of the Equation (1) in
to be a solution of the Equation (1) in  if and only if the system of the congruences
if and only if the system of the congruences
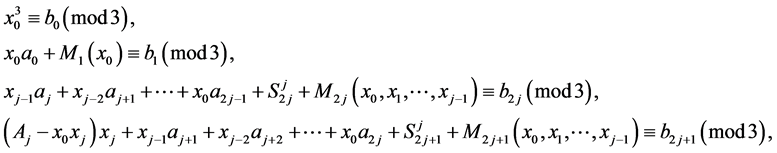
has a solution, where 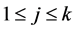 and integers
and integers  are defined from the equalities
are defined from the equalities
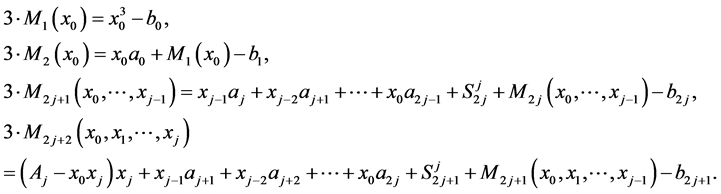
Theorem 3.9 Let 
 and
and  to be so that
to be so that  for all
for all  Then
Then  to be a solution of the Equation (1) in
to be a solution of the Equation (1) in  if and only if the system of the congruences
if and only if the system of the congruences
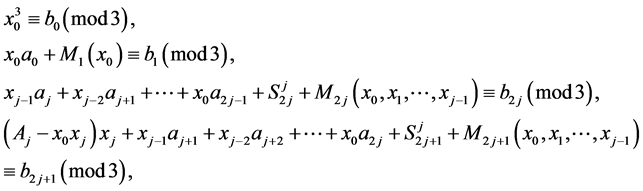
has a solution, where  and integers
and integers  are defined from the equalities
are defined from the equalities
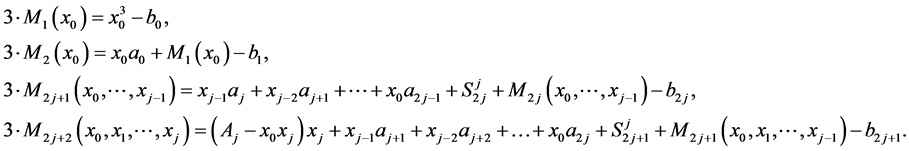
Acknowledgements
The first author was supported by grant UniKL/IRPS/str11061, Universiti Kuala Lumpur.