Computing Approximation GCD of Several Polynomials by Structured Total Least Norm ()
1. Introduction
Let  be the degree of
be the degree of  and
and  be the set of univariate polynomials.
be the set of univariate polynomials.  stands for the spectral norm of the matrix
stands for the spectral norm of the matrix .
. 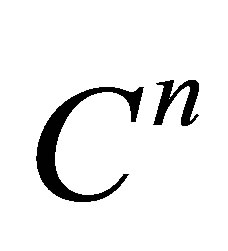 and
and  are the vector spaces of complex
are the vector spaces of complex 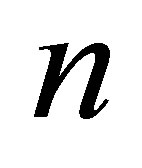 vectors and
vectors and 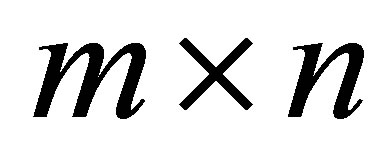 matrices, respectively. Transpose matrices and vectors are denoted by
matrices, respectively. Transpose matrices and vectors are denoted by 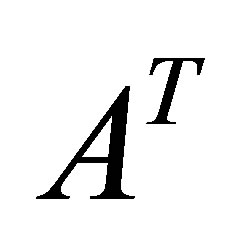 and
and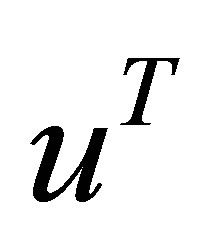 .
.  denotes the greatest common divisor for the polynomials
denotes the greatest common divisor for the polynomials  and
and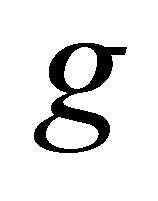 . We use
. We use 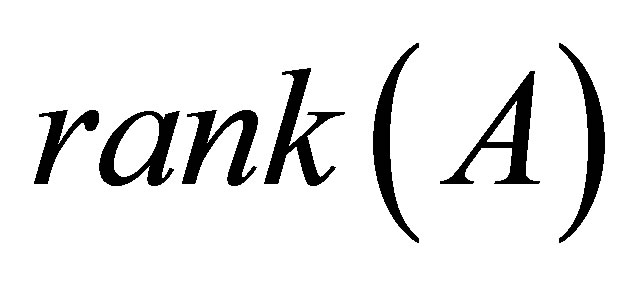 to stand for the rank of matrix
to stand for the rank of matrix .
.
In this paper, we consider the following problem. Let 

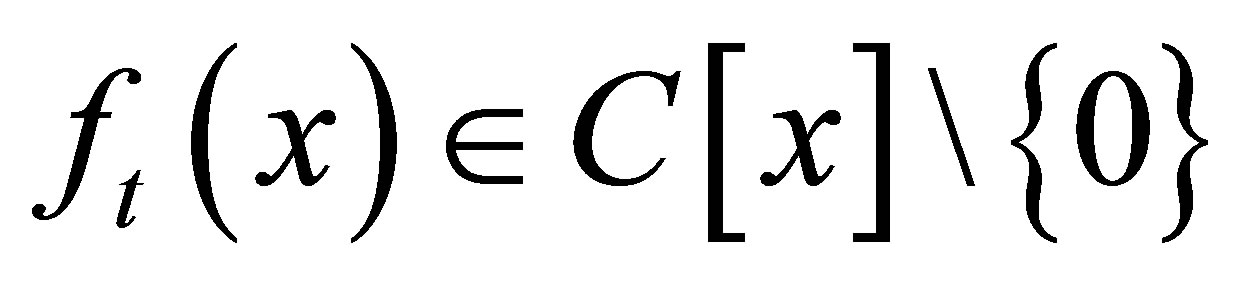 , namely
, namely
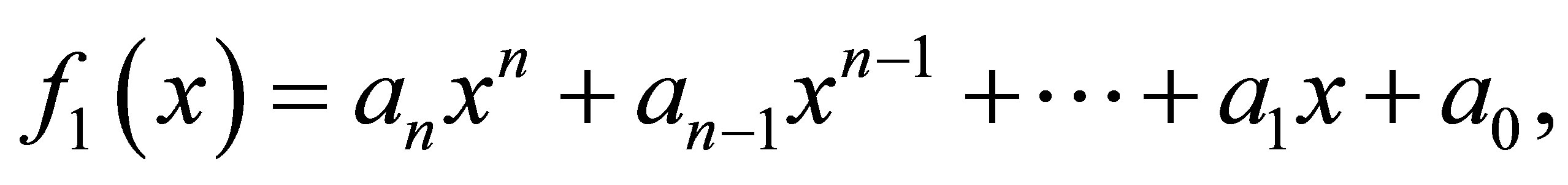
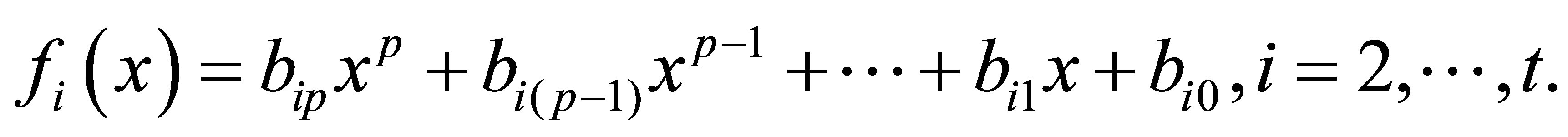
Problem 1.1. Set  be a positive integer with
be a positive integer with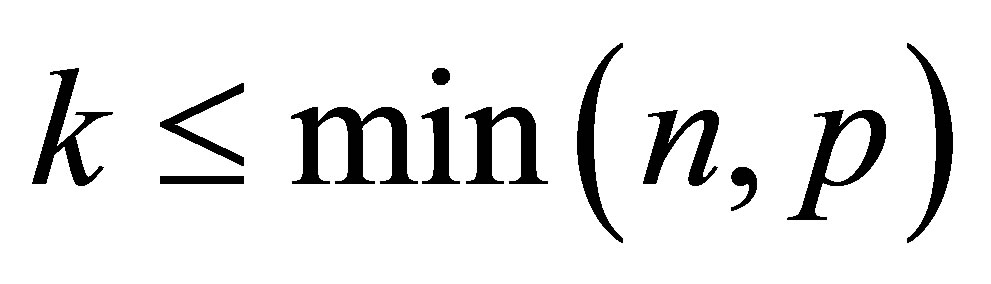 . We wish to compute
. We wish to compute 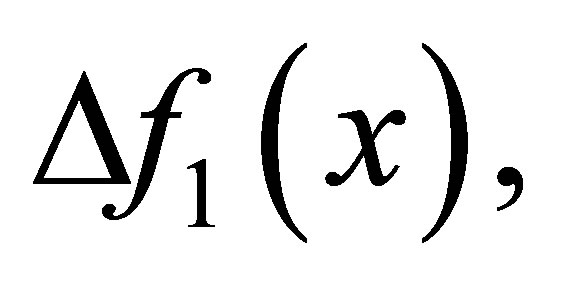


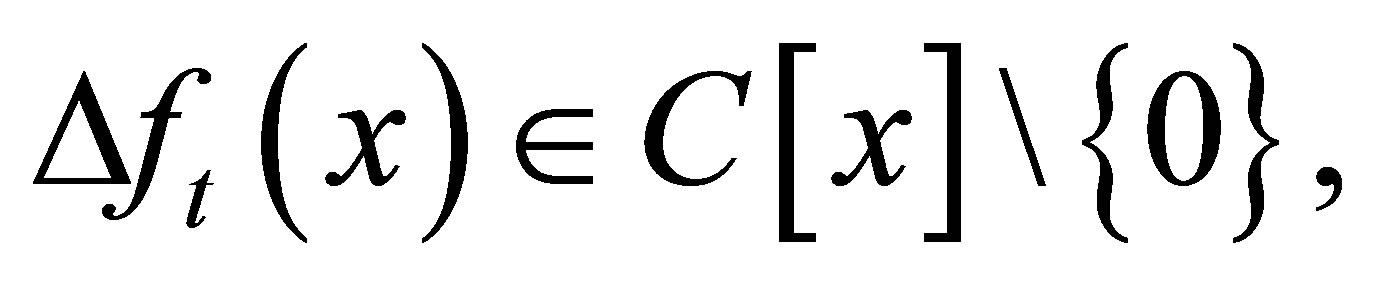 such that
such that


and
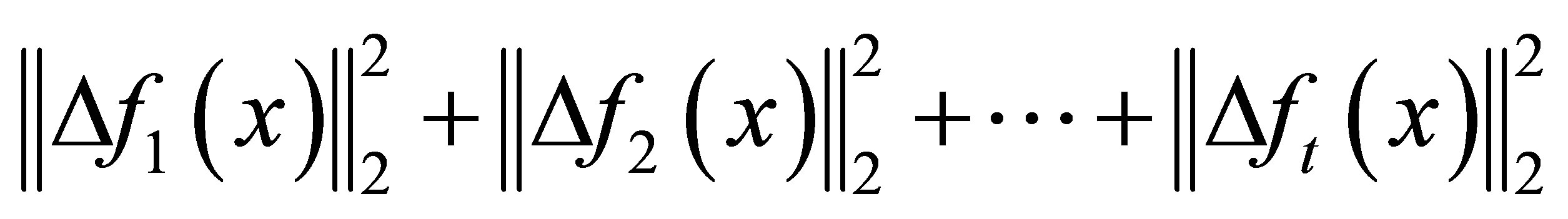
is minimized.
The problem of computing approximate GCD of several polynomials is widely applied in speech encoding and filter design [1], computer algebra [2] and signal processing [3] and has been studied in [4-7] in recent years. Several methods to the problem have been presented. The generally-used computational method is based on the truncated singular decomposition (TSVD) [8] which may not be appropriate when a matrix has a special structure since they do not preserve the special structure (for example, Sylvester matrix). Another common method based on QR decomposition [9,10] may suffer from loss of accuracy when it is applied to ill-conditioned problems and the algorithm derived in [11] can produce a more accurate result for ill-conditioned problems. Cadzow algorithm [12] is also a popular method to solve this problem which has been rediscovered in the literature [13].
Somehow it only finds a structured low rank matrix that is nearby a given target matrix but certainly is not the closet even in the local sense. Another method is based on alternating projection algorithm [14]. Although the algorithm can be applied to any low rank and any linear structure, the speed may be very slow. Some other methods have been proposed such as the ERES method [15], STLS method [16] and the matrix pencil method [17]. An approach to be described is called Structured Total Least Norm (STLN) which has been described for Hankel structure low rank approximation [18,19] and Sylvester structure low rank approximation with two polynomials [20]. STLN is a problem formulation for obtaining an approximate solution 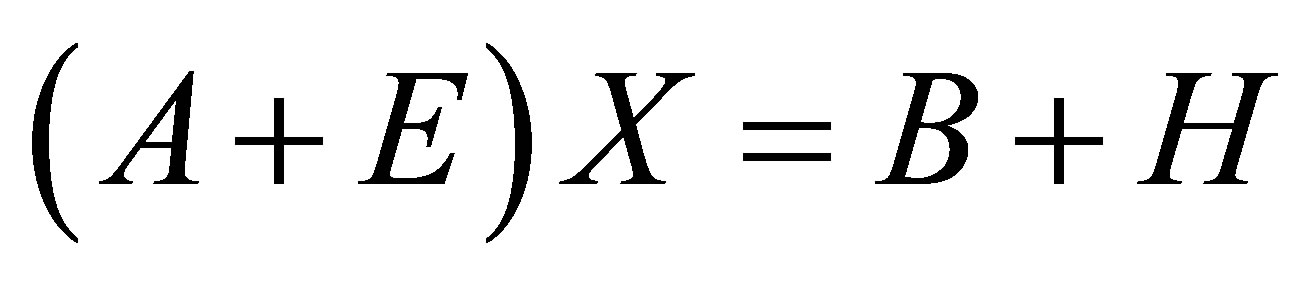 to an overdetermined linear system
to an overdetermined linear system 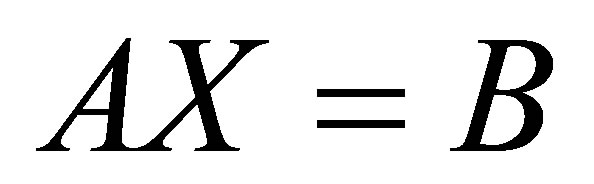 preserving the given structure in
preserving the given structure in  or
or .
.
In this paper, we apply the algorithm to compute the structured preserving rank reduction of Sylvester matrix. We introduce some notations and discuss the relationship between the GCD problems and low rank approximation of Sylvester matrices in Section 2. Based on STLN method, we describe the algorithm to solve Problem 1.1 in Section 3. In Section 4, we use some examples to illustrate the method is feasible.
2. Main Results
First of all, we shall prove that Problem 1.1 always has a solution.
Theorem 2.1. Suppose that 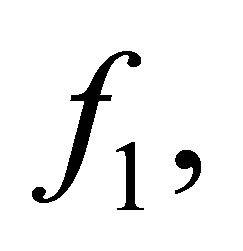
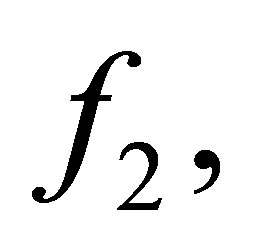

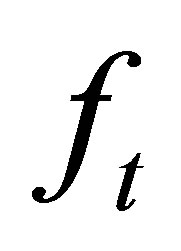 ,
, 

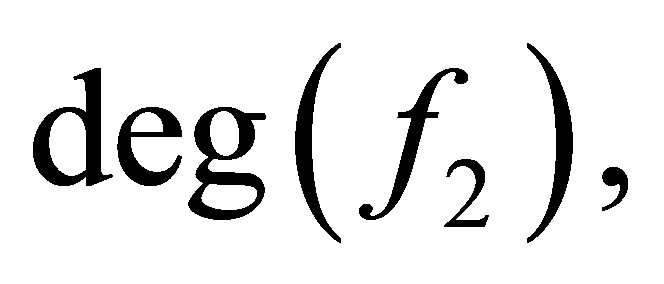
 and
and 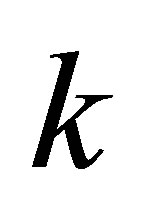 are defined as those in Problem 1.1. There exist
are defined as those in Problem 1.1. There exist ,
, 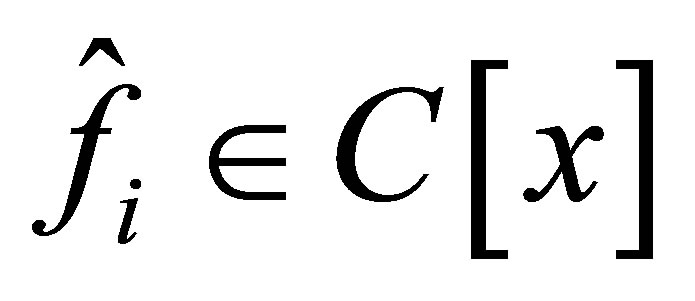 with
with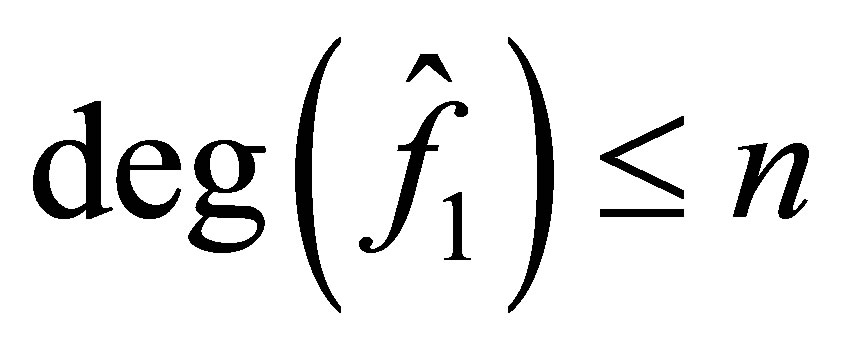 ,
, 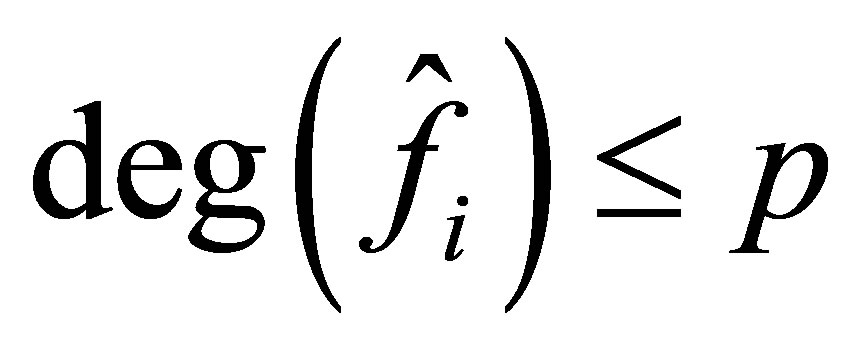 and
and
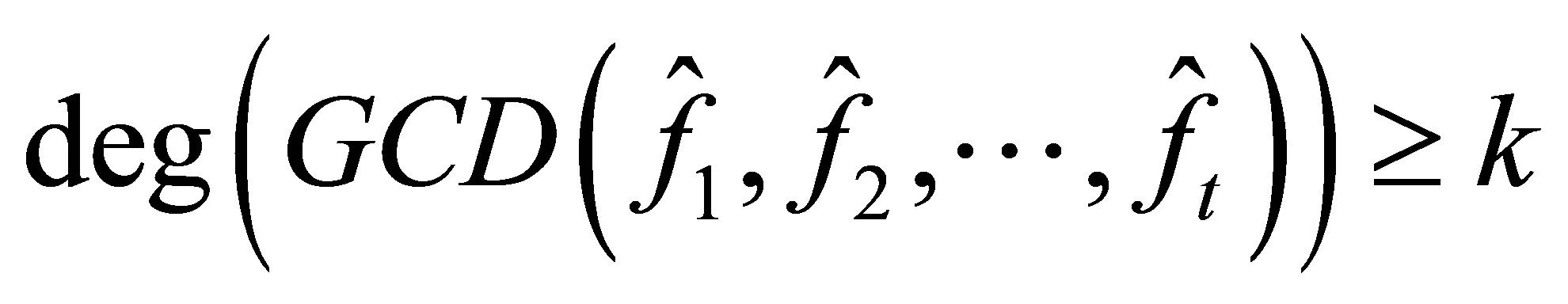 such that for all
such that for all ,
, 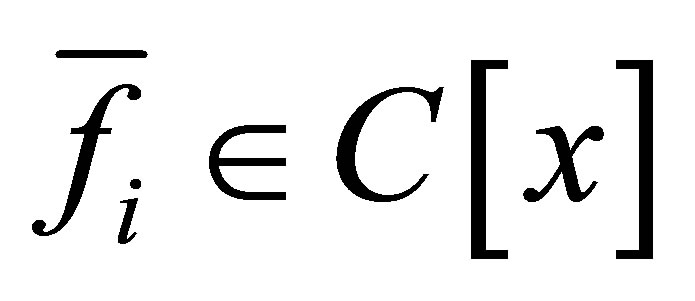 with
with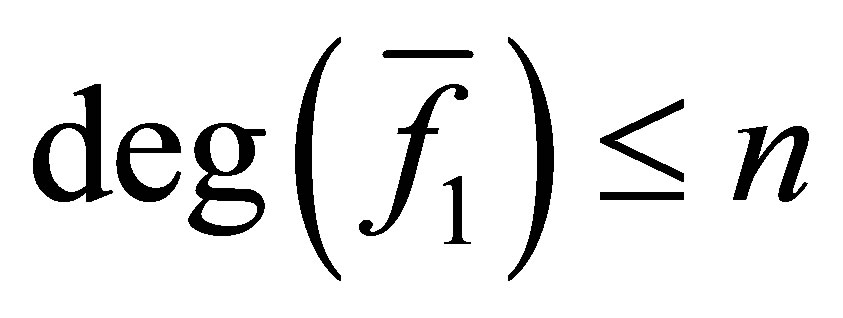 ,
, 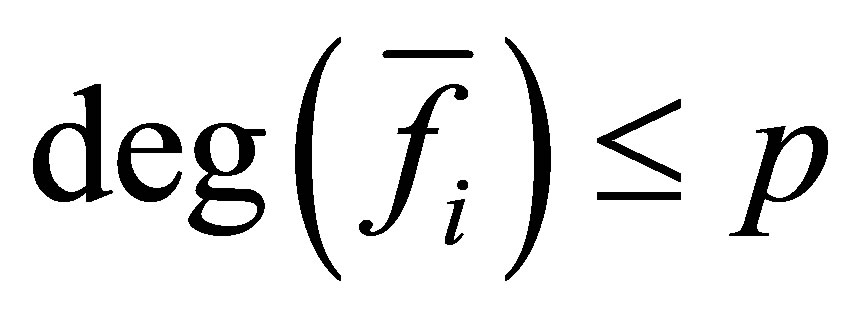 and
and
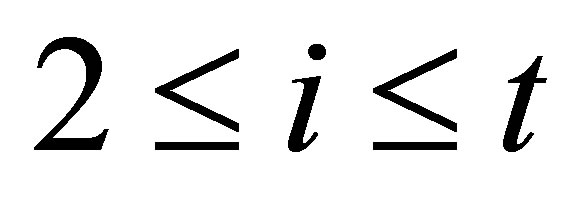
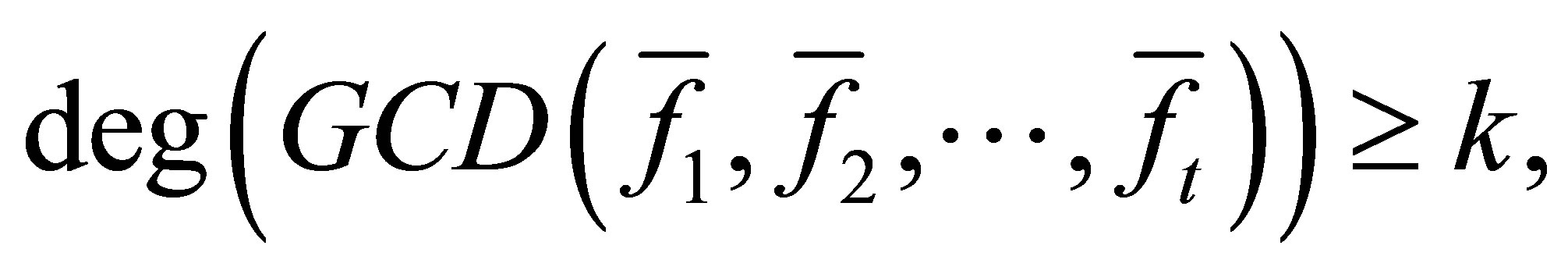 .
.
We have

Proof. Let  be monic with
be monic with 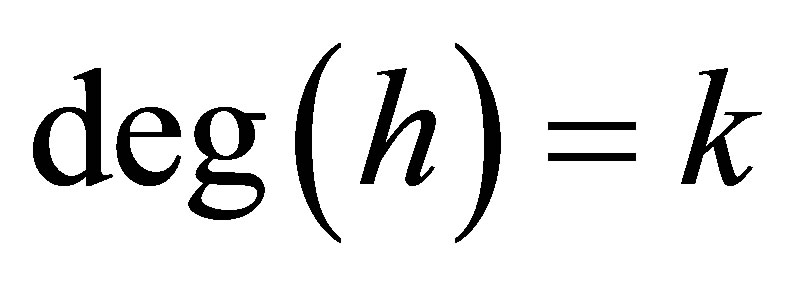 and set
and set  with
with . For the real and imaginary parts of the coefficients of
. For the real and imaginary parts of the coefficients of  and of
and of 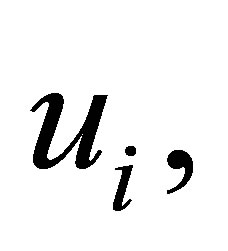
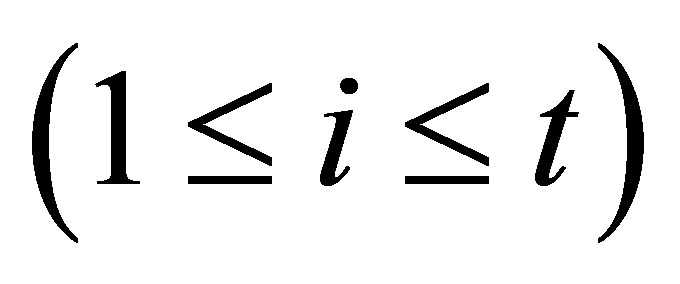 . We are considered with the continuous objective function
. We are considered with the continuous objective function
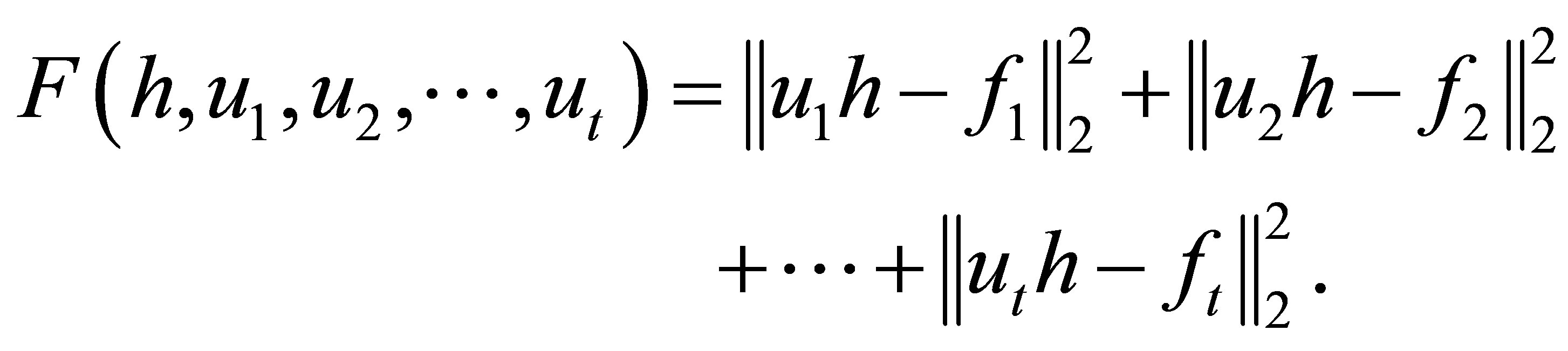
We will prove that the function has a value on a closed and bounded set of its real argument vector which is smaller than elsewhere. Consider 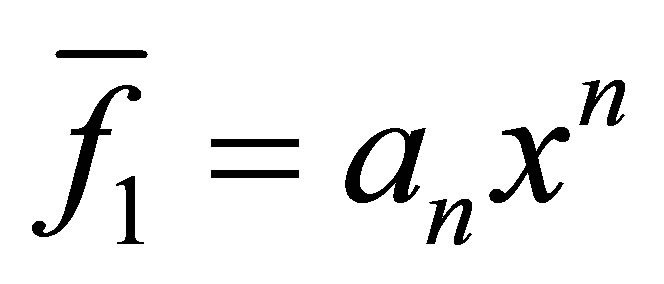 and
and  with a GCD of degree
with a GCD of degree  for
for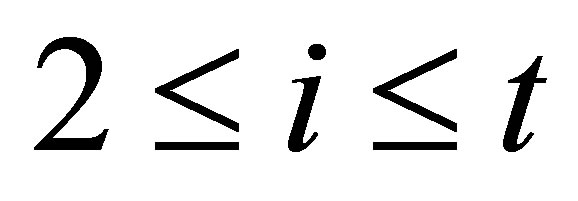 . Clearly, any
. Clearly, any  and
and  with
with
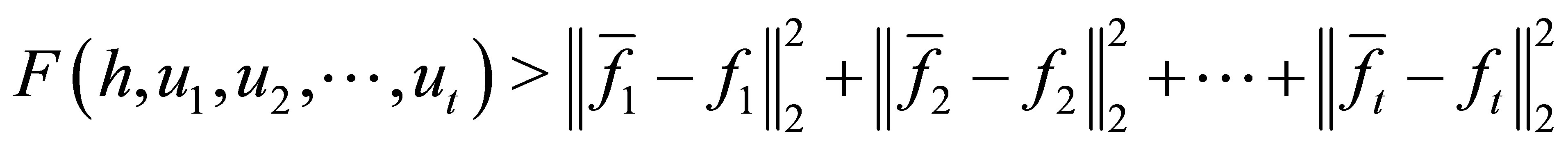
can be discarded. So from above,we know that the coefficients of 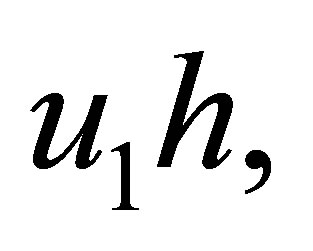
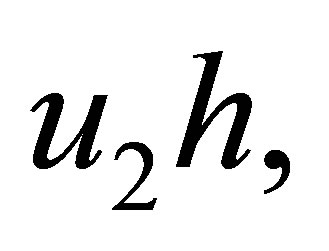

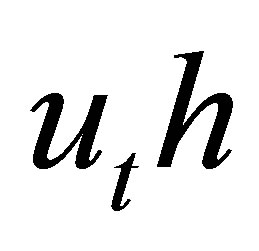 can be bounded and so can the coefficients of
can be bounded and so can the coefficients of 



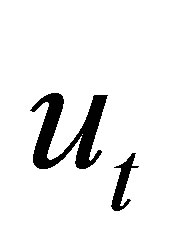 by any polynomials factor coefficient bound. Thus the function’s domain
by any polynomials factor coefficient bound. Thus the function’s domain 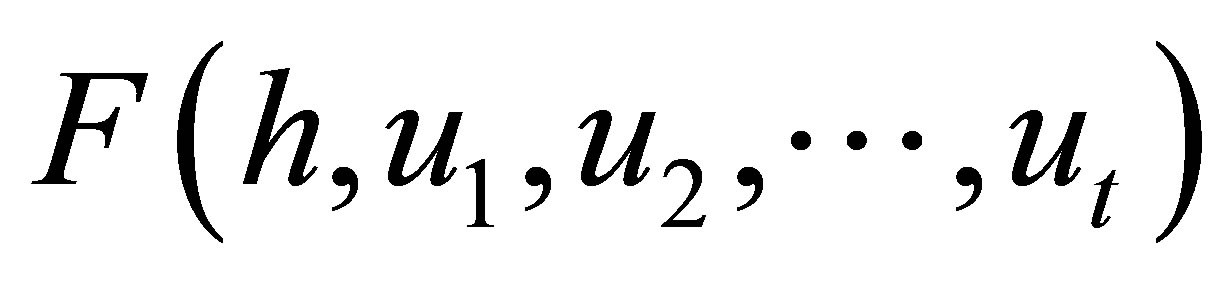 is restricted to a sufficiently large ball. It remains to exclude
is restricted to a sufficiently large ball. It remains to exclude 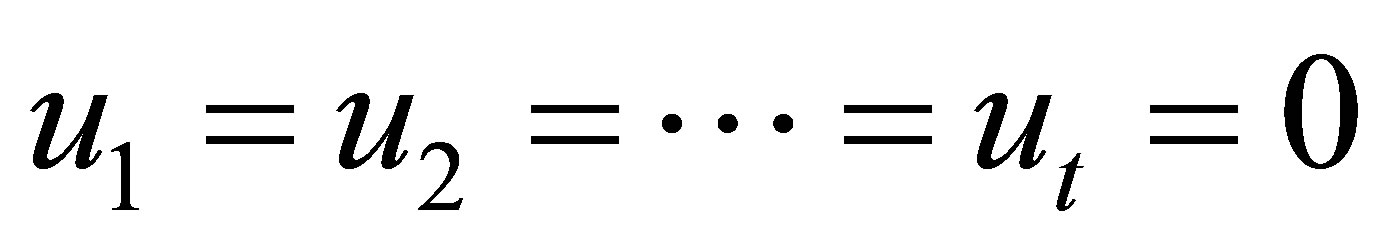 as the minimal solution. We have
as the minimal solution. We have
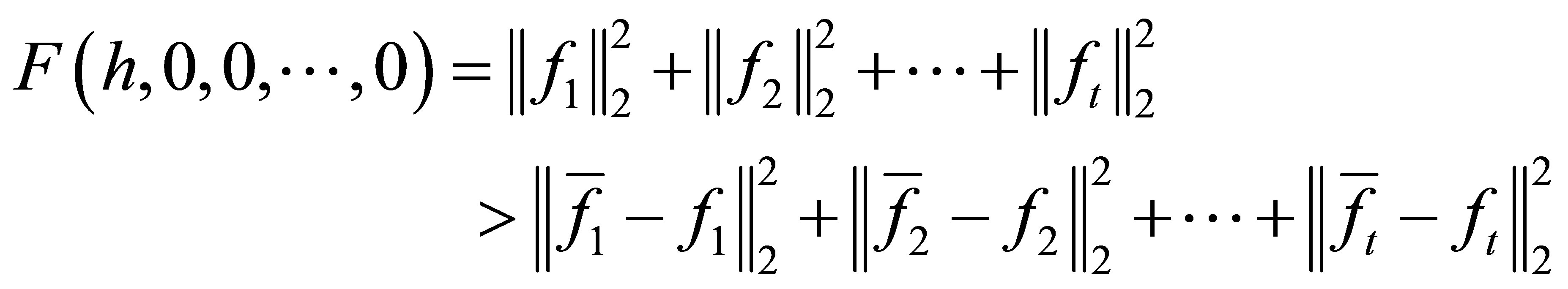 .
.
In conclusion, the theorem is true.
Now we begin to solve Problem 1.1, we first define a 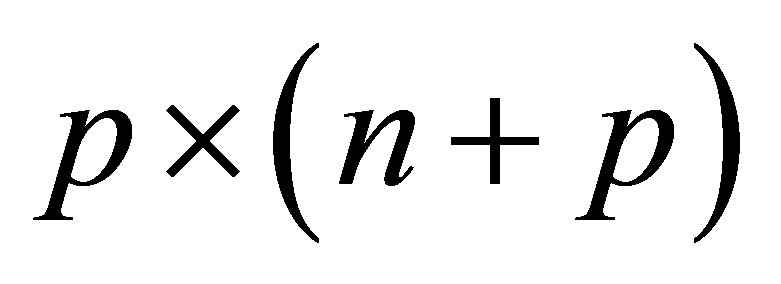 matrix associated with
matrix associated with  as follows
as follows

and an  matrix associated with
matrix associated with 
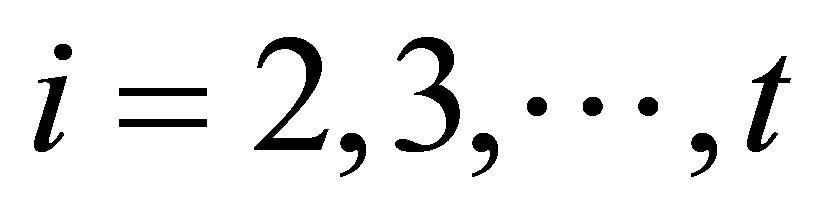 as
as
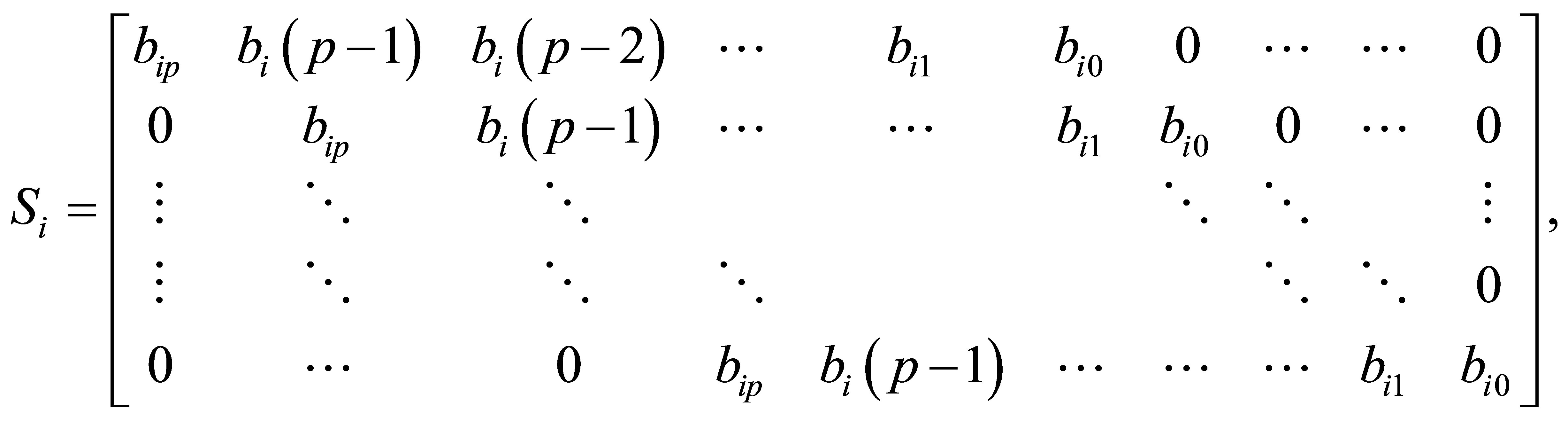
An extended Sylvester matrix or a generalized resultant is then defined by

Deleting the last  rows of
rows of  and the last
and the last 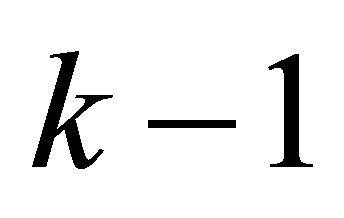 columns of coefficients of
columns of coefficients of  separately is
separately is , We get the
, We get the  -th Sylvester matrix
-th Sylvester matrix 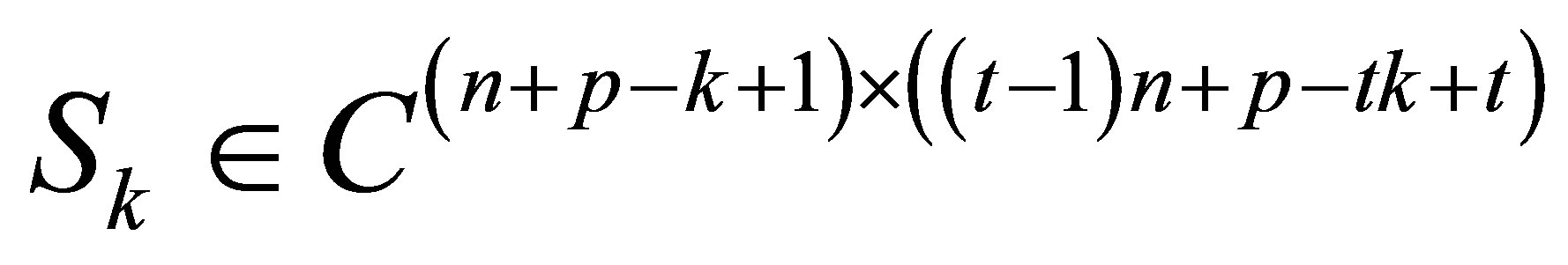

It is well-known that 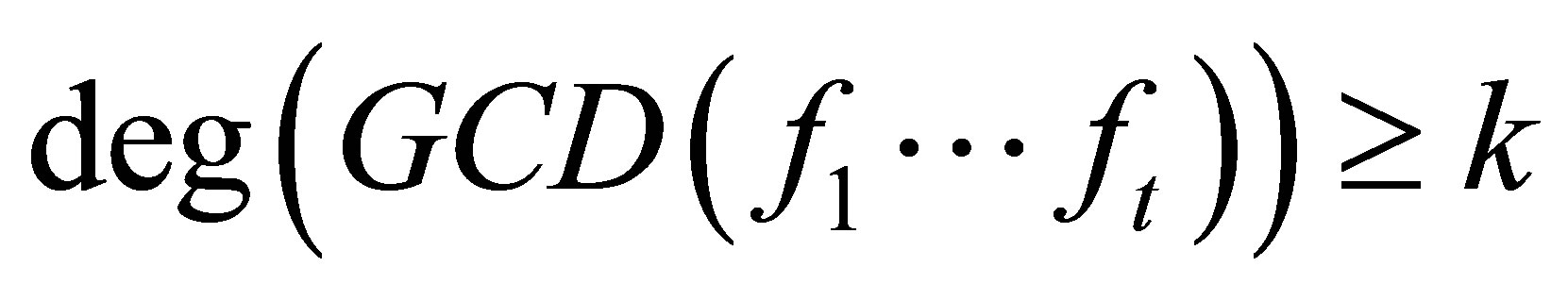 if and only if
if and only if 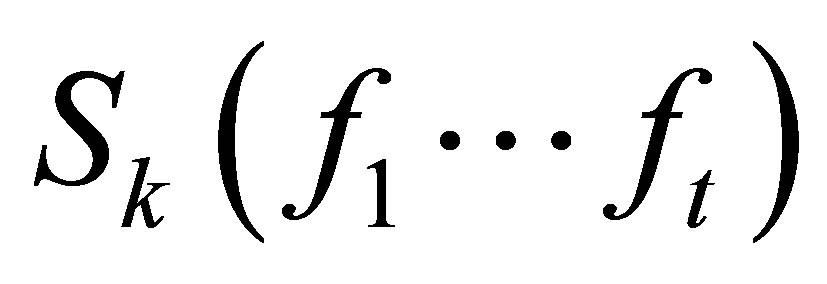 has rank deficiency at least 1. We have
has rank deficiency at least 1. We have

(2.1)
where 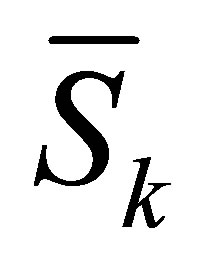 is the
is the 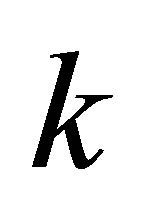 -th Sylvester matrix generated by
-th Sylvester matrix generated by 
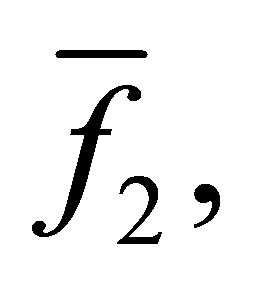

 .
.
From above, we know that (2.1) can be transformed to the low rank approximation of a Sylvester matrix.
If we use STLN [16] to solve the following overdetermined system
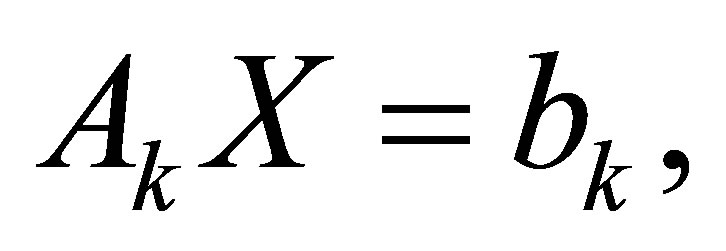
for , where
, where 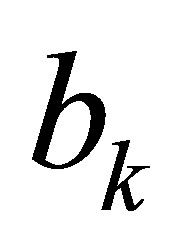 is the first column of
is the first column of  and
and 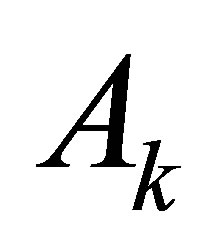 are the remainder columns of
are the remainder columns of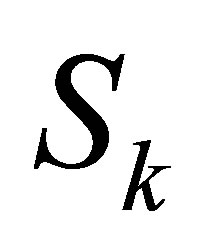 , then we get a minimal perturbation
, then we get a minimal perturbation 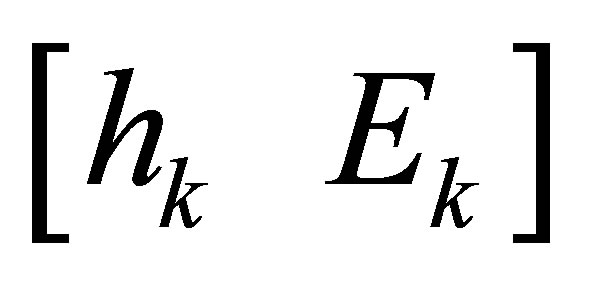 of Sylvester structure satisfying
of Sylvester structure satisfying

So the solution with Sylvester structure is 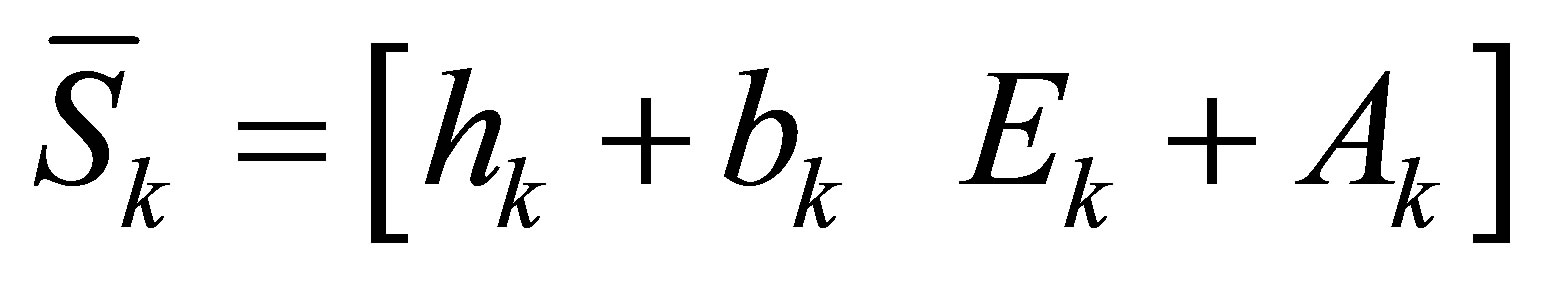 and
and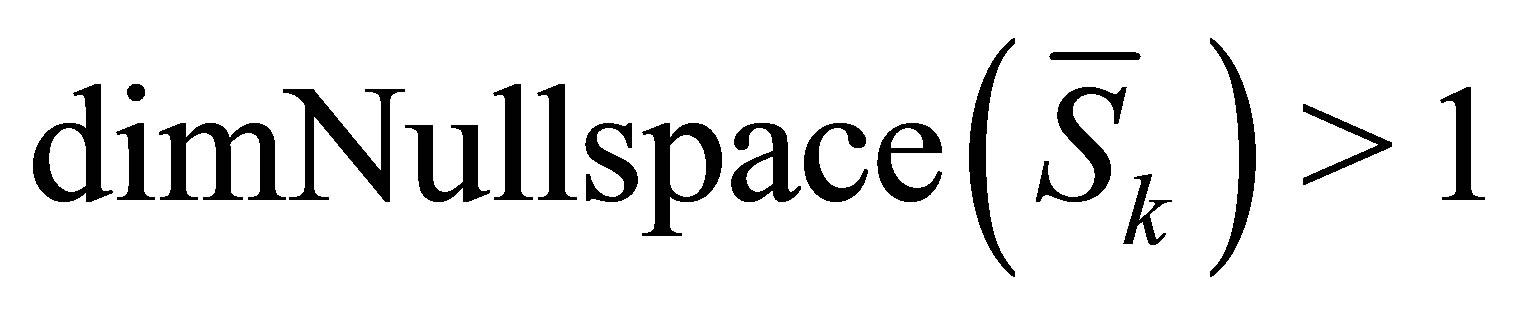 .
.
We will give the following example and theorem to explain why we choose the first column to form the overdetermined system.
Example 2.1. Suppose three polynomials are given
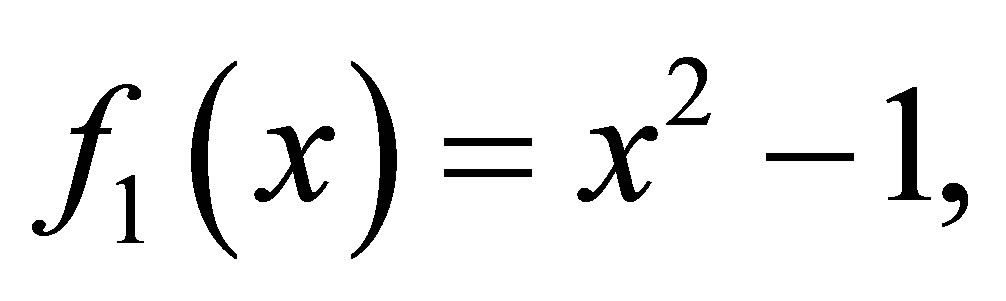

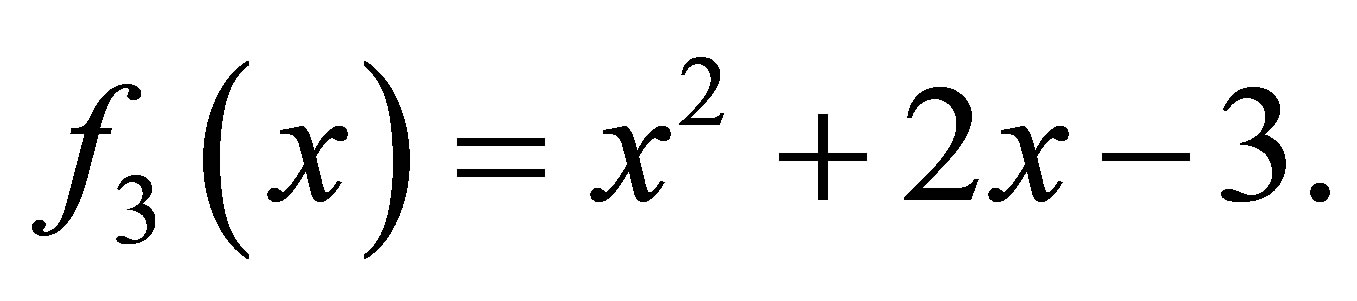
The matrix 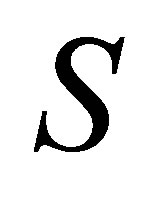 is the Sylvester matrix generated by
is the Sylvester matrix generated by

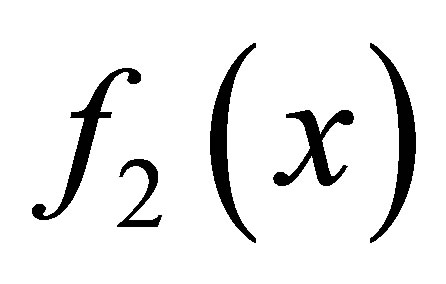 and
and 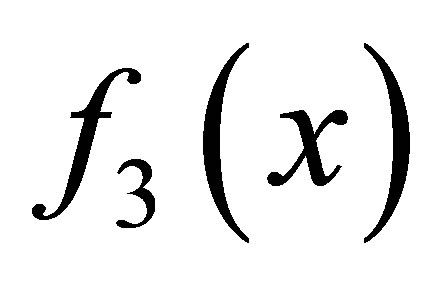
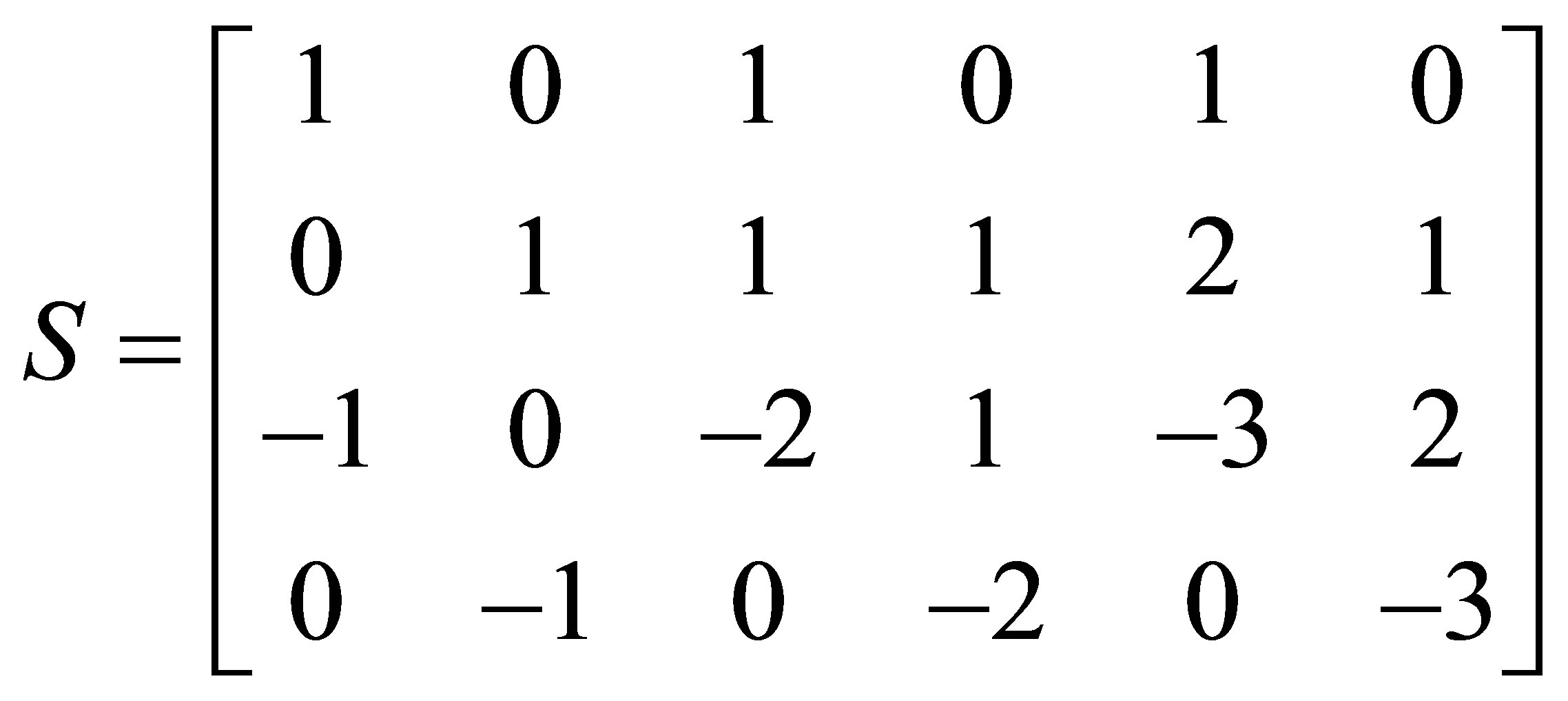
The matrix 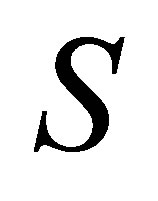 is partitioned as
is partitioned as 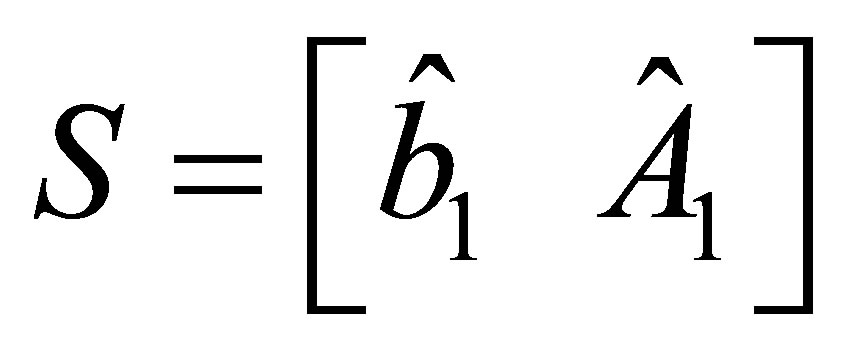 or
or , where
, where  is the first column of
is the first column of , whereas
, whereas 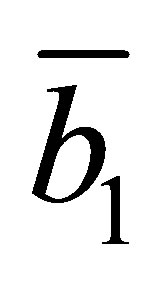 is the last column of
is the last column of .
.
The overdetermined system
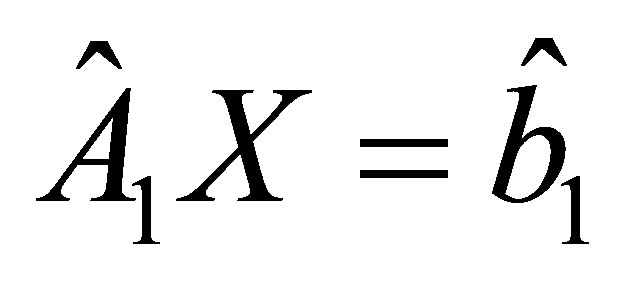
has a solution , while the system
, while the system
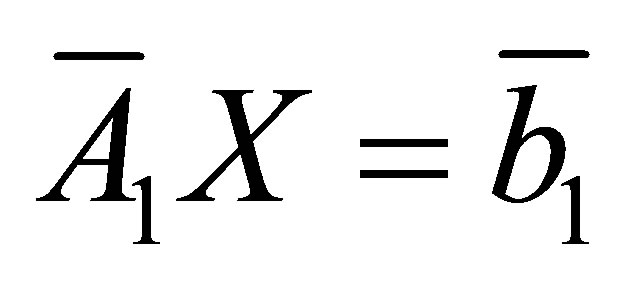
has no solution.
Theorem 2.2. Suppose that 


 ,
, 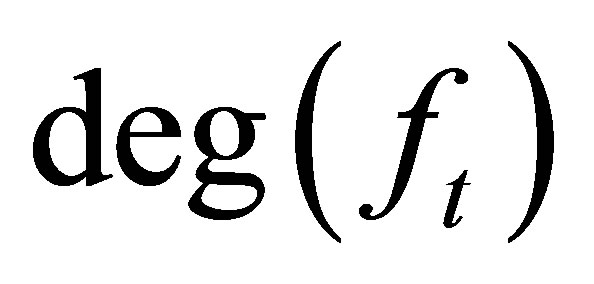


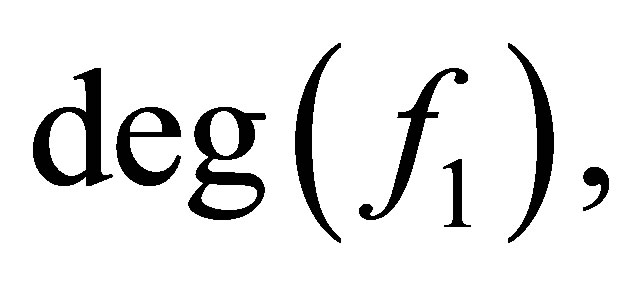 and
and  are defined as those in Problem 1.1 and
are defined as those in Problem 1.1 and 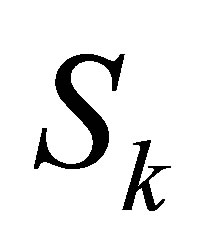 is the
is the 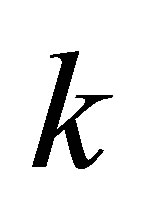 -th Sylvester matrix of
-th Sylvester matrix of 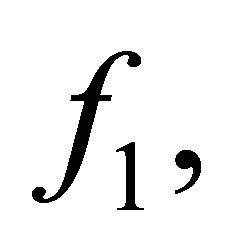
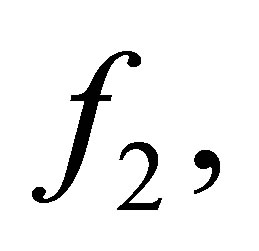

 . Then the following statements are equivalent.
. Then the following statements are equivalent.
1)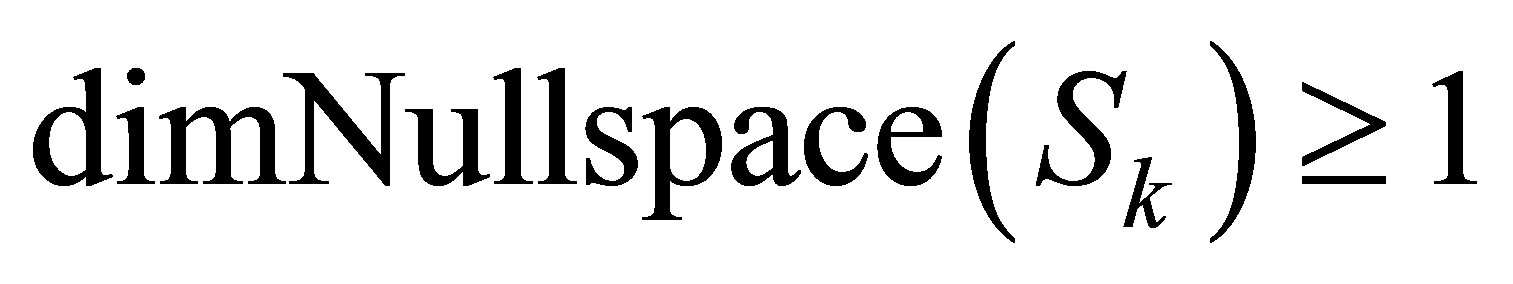 ;
;
2)  has a solution, where
has a solution, where 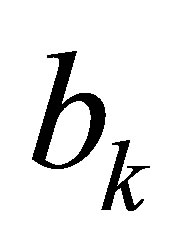 is the first column of
is the first column of 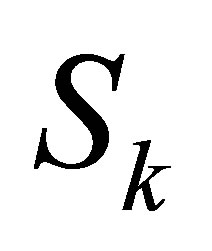 and
and 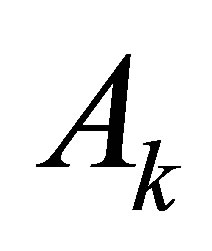 are the remainder columns of
are the remainder columns of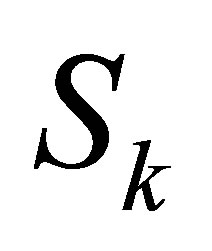 .
.
Proof.  Suppose
Suppose 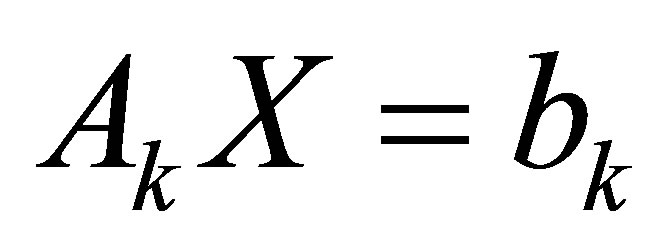 has a nonzero solution, then
has a nonzero solution, then . Since
. Since 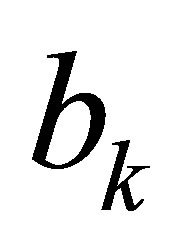 is the first column of
is the first column of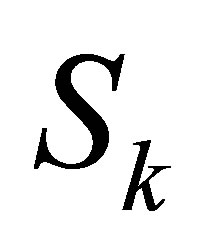 , obviously, the dimension of the rank deficiency of
, obviously, the dimension of the rank deficiency of 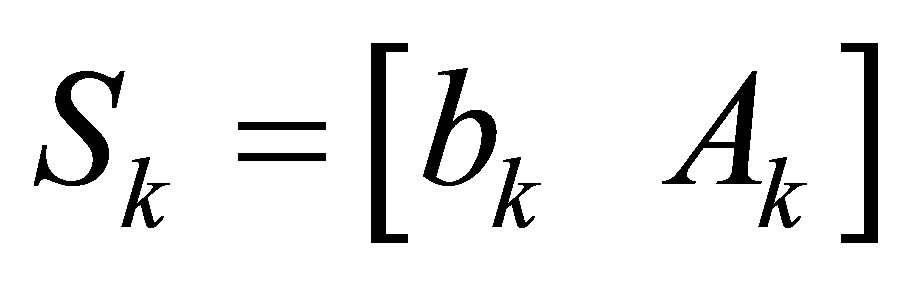 is at least 1.
is at least 1.
 Suppose the rank deficiency of
Suppose the rank deficiency of 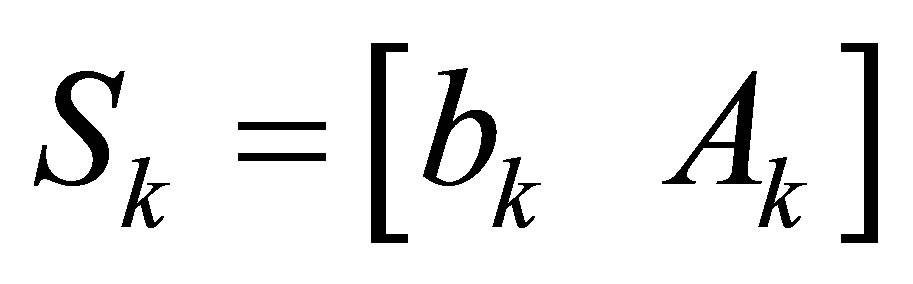 is at least 1 and
is at least 1 and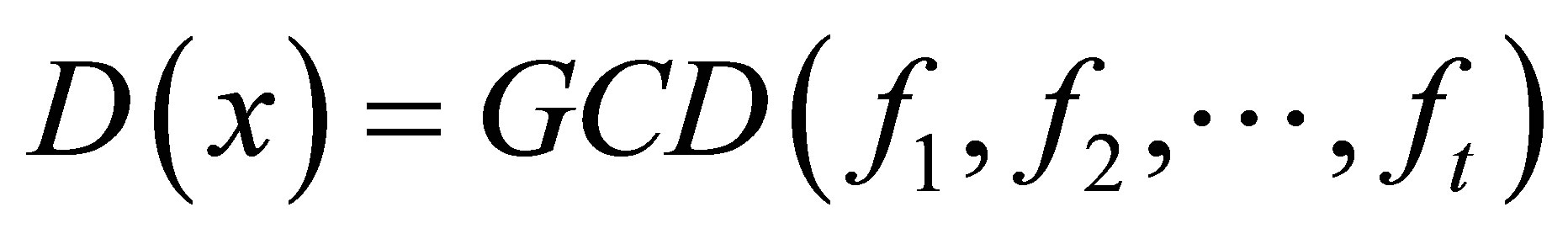 ,
, 
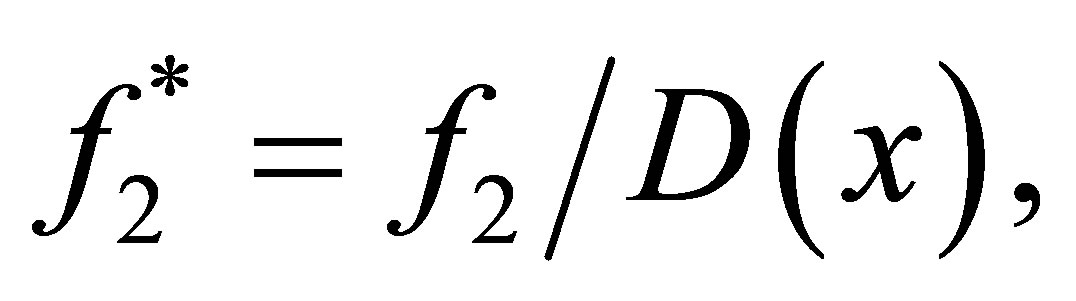

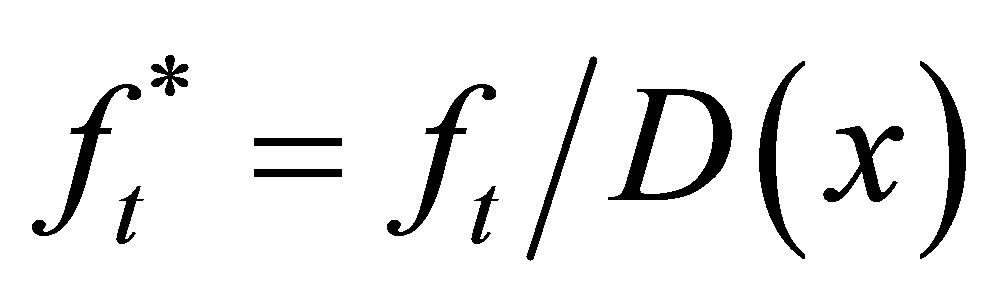 . Multiplying the vector
. Multiplying the vector  to the matrix
to the matrix , then we obtain
, then we obtain
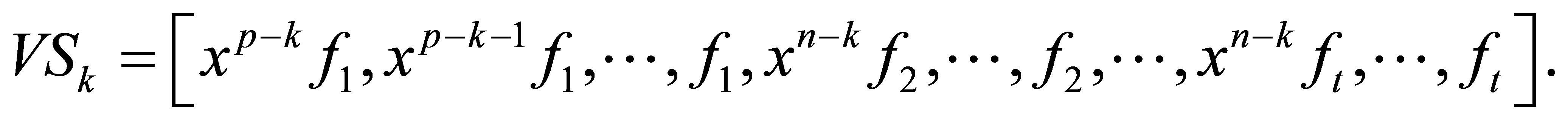 (2.2)
(2.2)
Next we will prove that 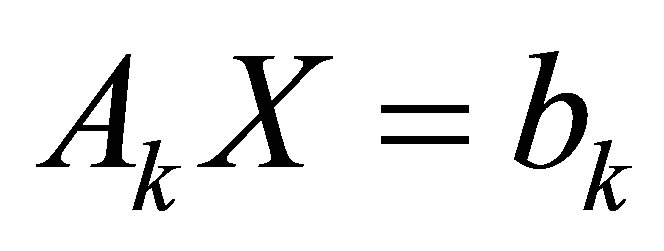 has a solution. If we multiply the vector
has a solution. If we multiply the vector 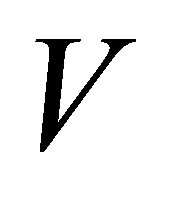 to two sides of the equation
to two sides of the equation , it turns out to be
, it turns out to be
 (2.3)
(2.3)
The solution  of equation (2.3) is equal to the coefficients of polynomials
of equation (2.3) is equal to the coefficients of polynomials 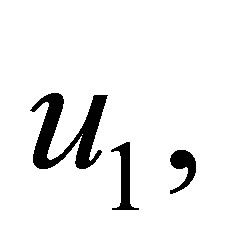
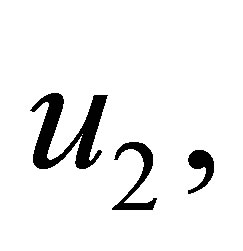

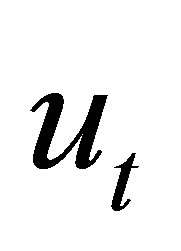 such that
such that
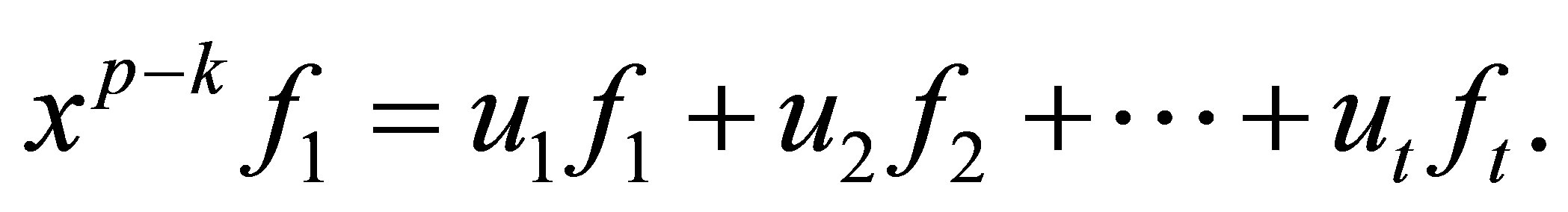
We can get  and
and 
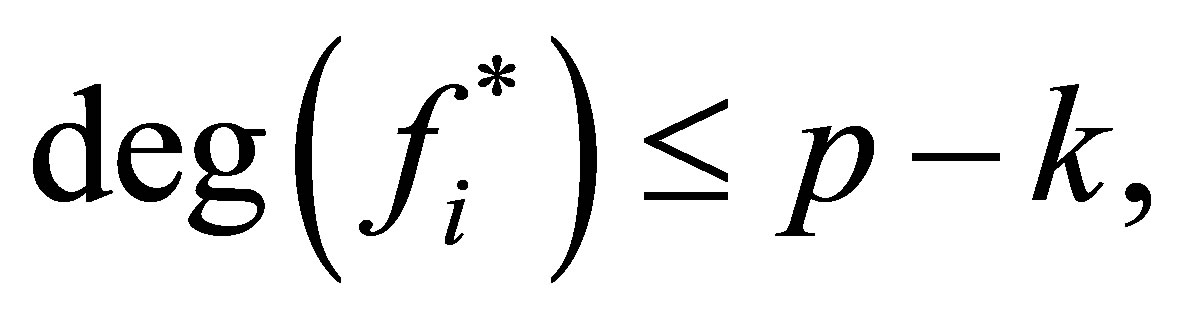
 from
from  . Dividing
. Dividing  by
by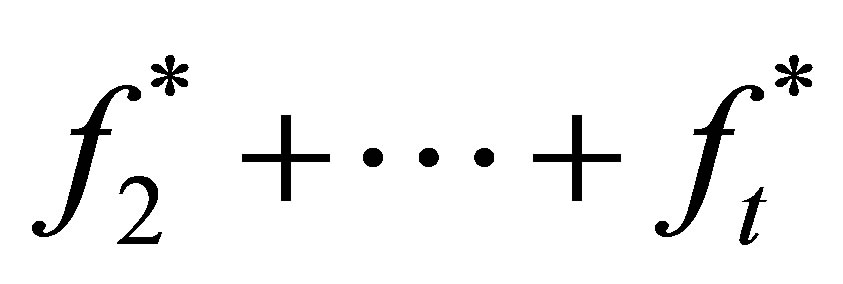 , we obtain a quotient
, we obtain a quotient 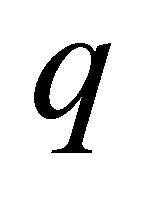 and a remainder
and a remainder 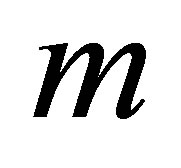 satisfy
satisfy
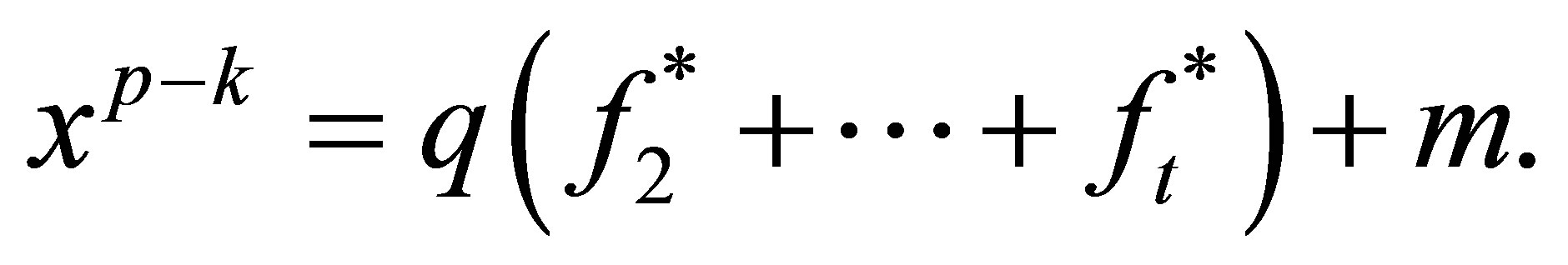
where 
 . Now we can get that
. Now we can get that

are solutions of Equation (2.3), since

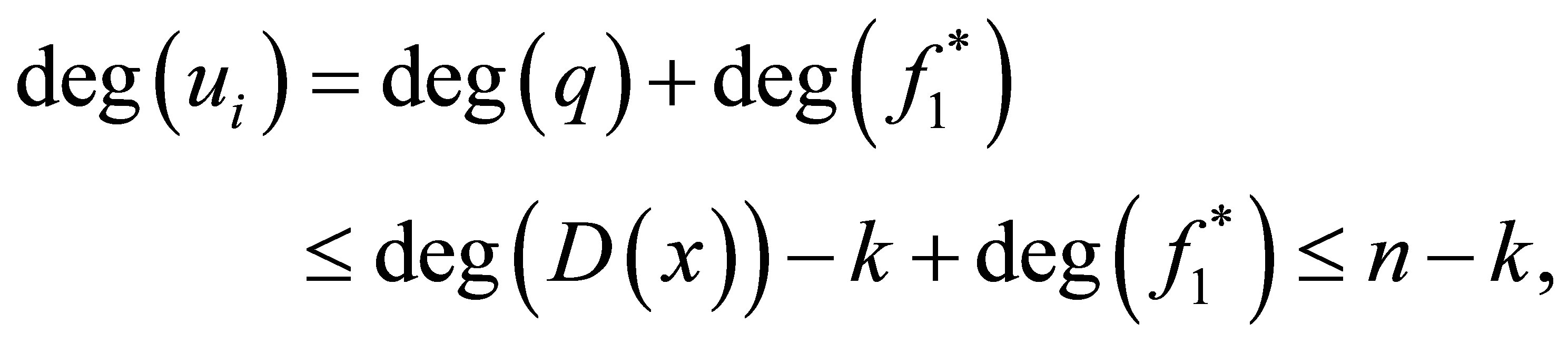
and

Next, we will illustrate for any given Sylvester matrixas long as all the elements are allowed to be perturbed, we can always find 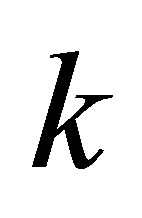 -Sylvester structure matrices
-Sylvester structure matrices  satisfy
satisfy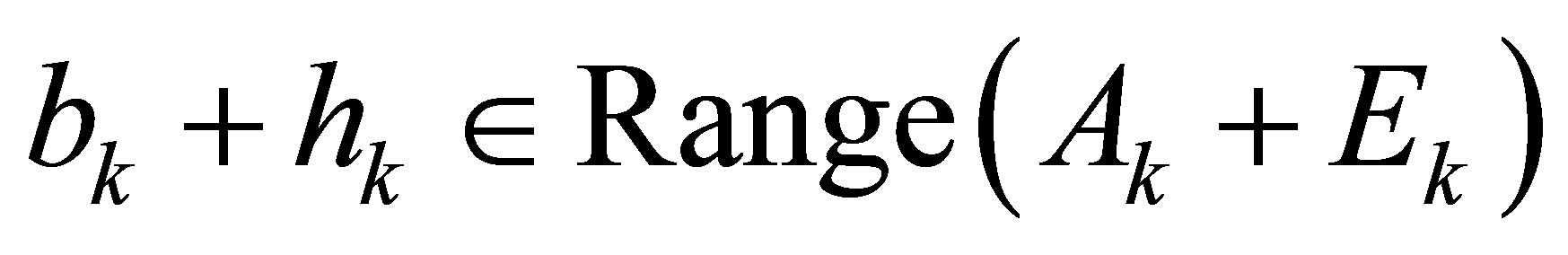 , where
, where  is the first column of
is the first column of 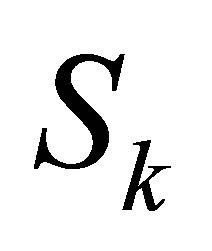 and
and 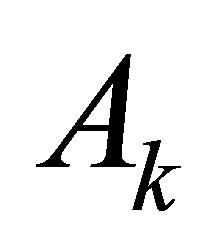 are the remainder column of
are the remainder column of .
.
Theorem 2.3. Given the positive integer , there exists a Sylvester matrix
, there exists a Sylvester matrix  with rank deficiency k.
with rank deficiency k.
Proof. We can always find polynomials  with
with ,
,  and
and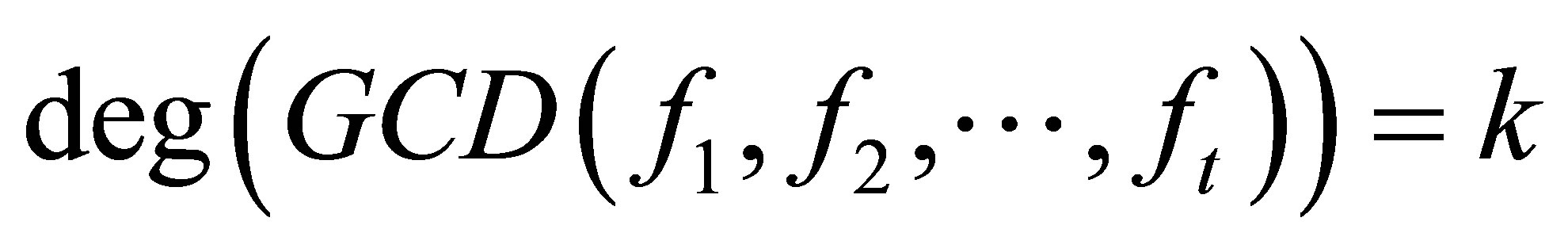 . Hence
. Hence 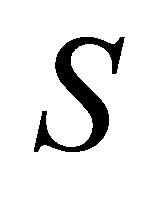 is the Sylvester matrix of
is the Sylvester matrix of 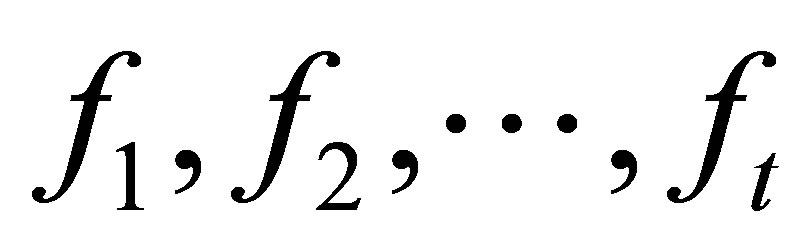 and its rank deficiency is k.
and its rank deficiency is k.
Corollary 2.1. Given the positive integer , and
, and 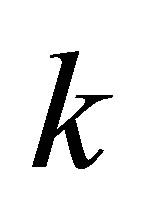 -th Sylvester matrix
-th Sylvester matrix , where
, where  ,
,  , it is always possible to find a
, it is always possible to find a 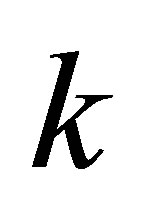 -th Sylvester structure perturbation
-th Sylvester structure perturbation 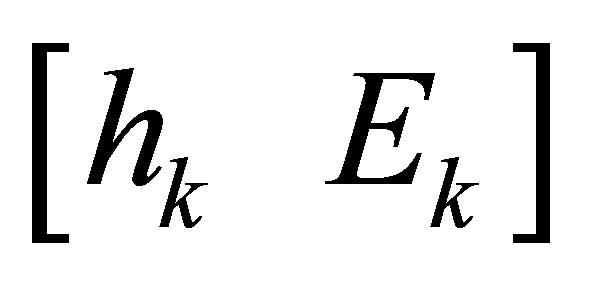 such that
such that .
.
3. STLN for Overdetermined System with Sylvester Structure
In this section, we will use STLN method to solve the overdetermined system
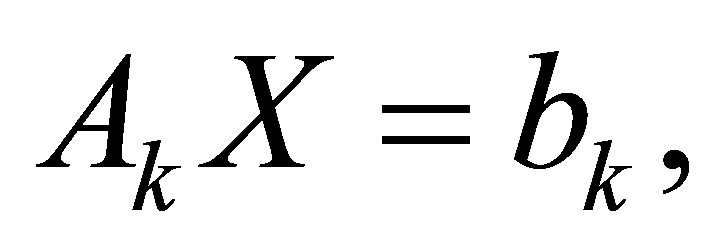
According to theorem 2.3 and corollary 2.1, we can always find Sylvester structure  with
with  . Next we will use STLN method to find the minimum solution.
. Next we will use STLN method to find the minimum solution.
First, we define the Sylvester structure preserving perturbation 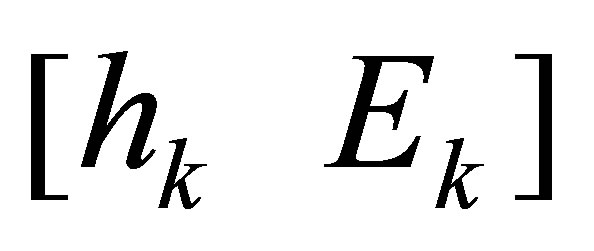 of
of 

can be represented by a vector
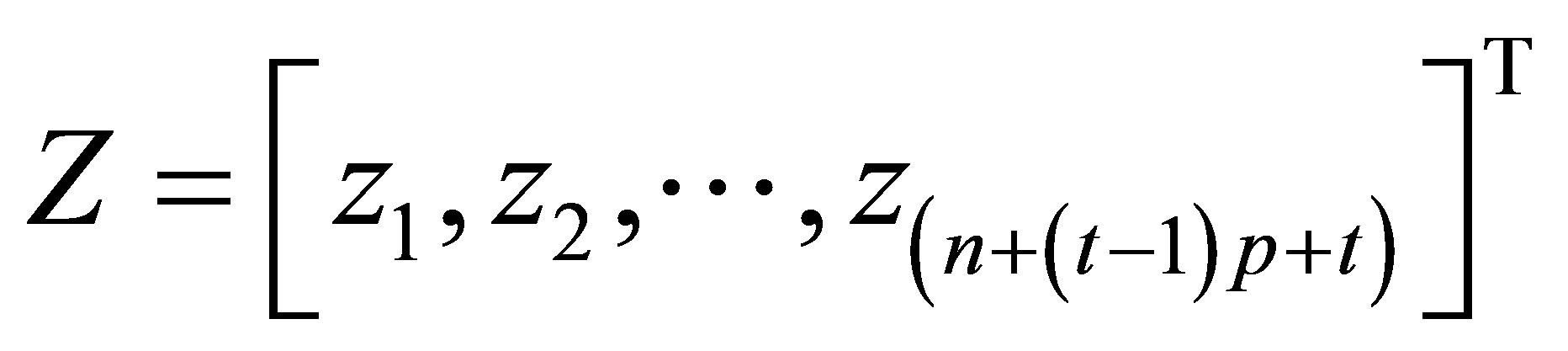 .
.
We can define a matrix  such that
such that .
.

where  is a
is a  identity matrix.
identity matrix.
We will solve the equality-constrained least squares problem
 (3.1)
(3.1)
where the structured residual  is
is
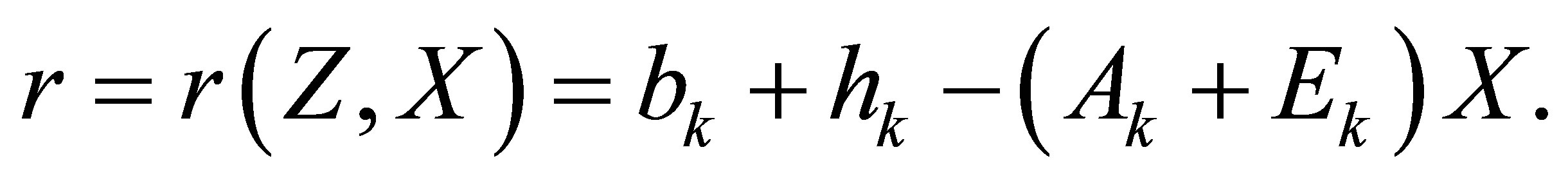
By using the penalty method, the formulation (3.1) can be transformed into
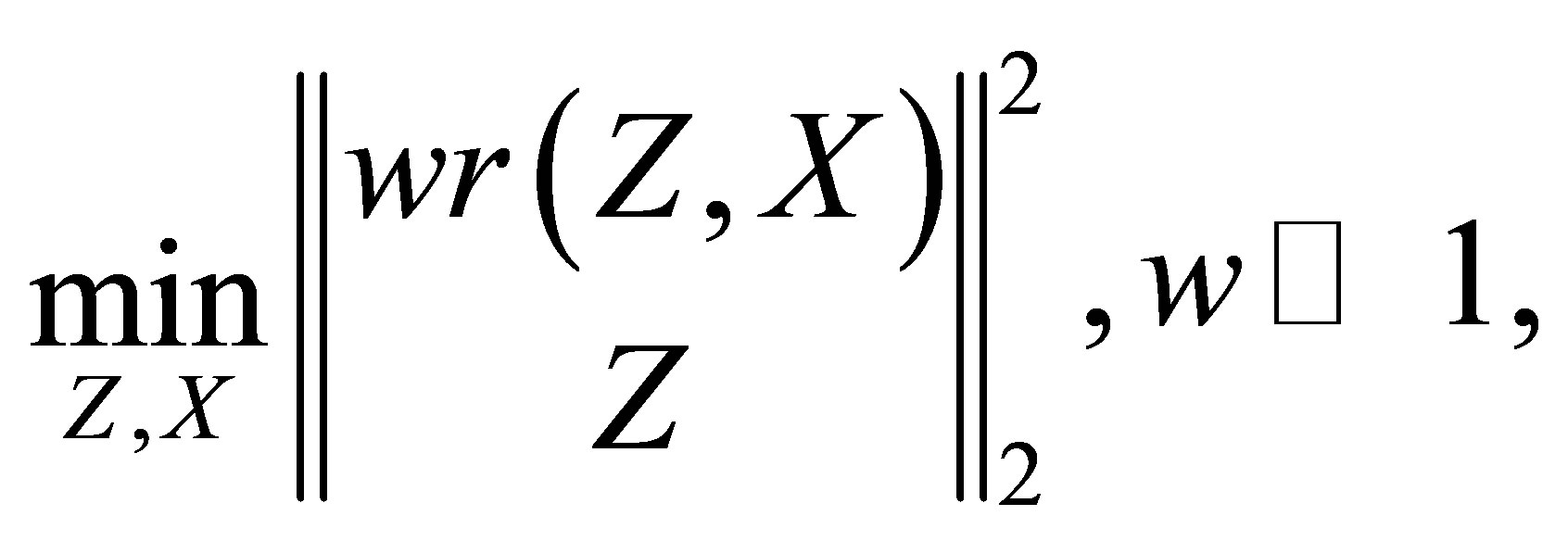 (3.2)
(3.2)
where  is a large penalty value.
is a large penalty value.
Let 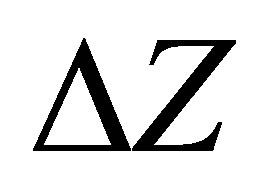 and
and 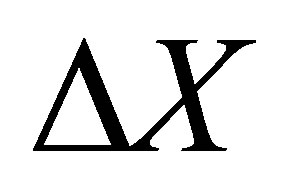 stand for a small change in
stand for a small change in 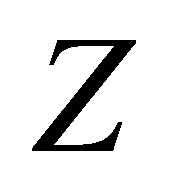 and
and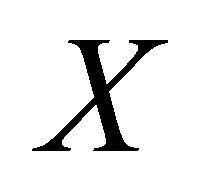 , respectively and
, respectively and  be the corresponding change in
be the corresponding change in . Then the first order approximate to
. Then the first order approximate to 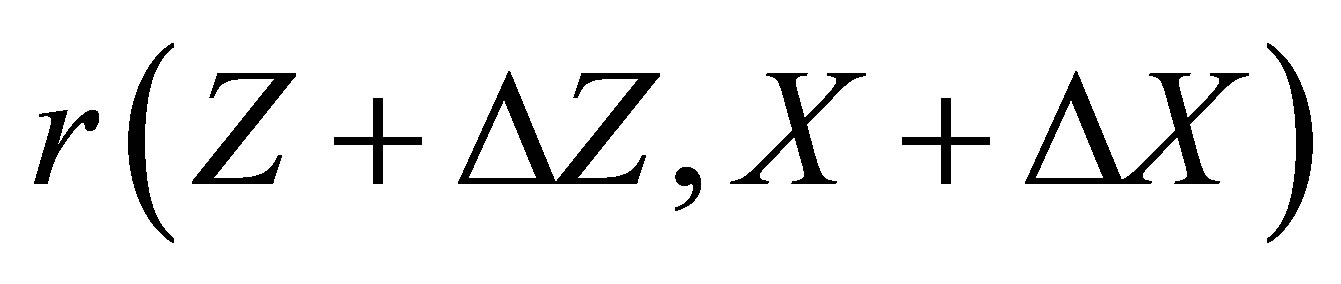 is
is
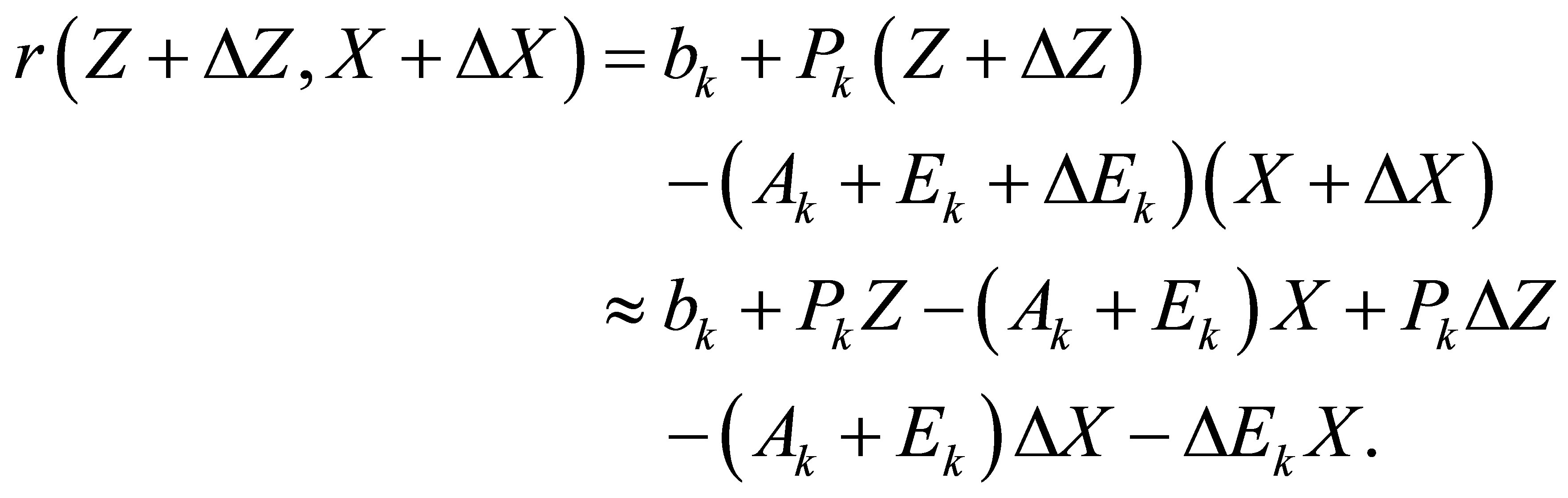
Introducing a matrix of Sylvester structure 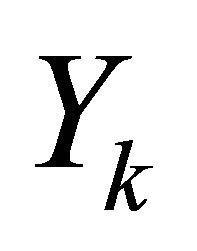 and
and

(3.2) can be approximated by
 (3.3)
(3.3)
where 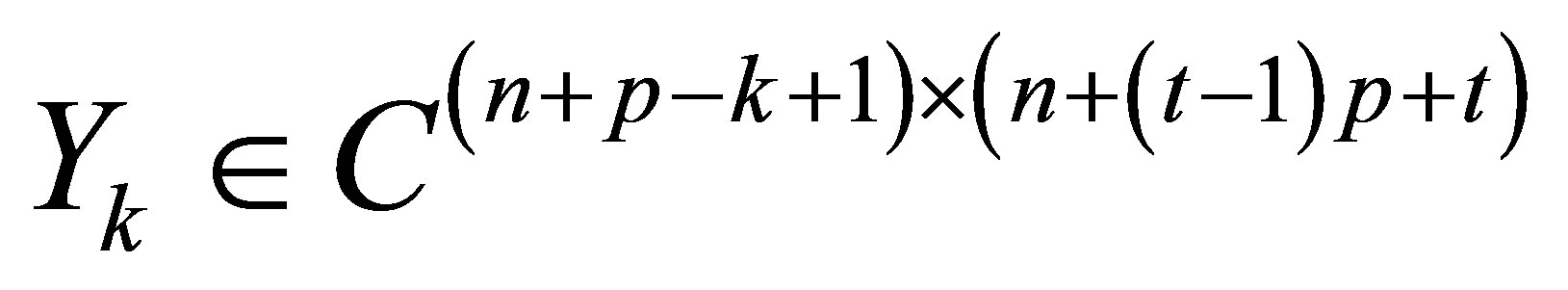 satisfies that
satisfies that
 (3.4)
(3.4)
In the following, we present a method to obtain the matrix . Suppose
. Suppose 


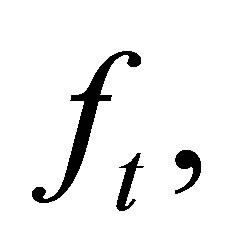
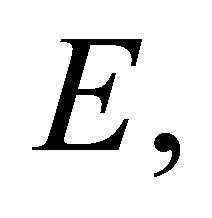
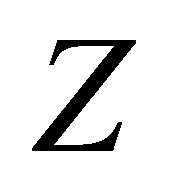 and
and 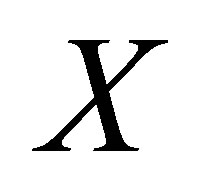 are defined as above. Multiplying the vector
are defined as above. Multiplying the vector

to the two sides of equation (3.4), it becomes

Let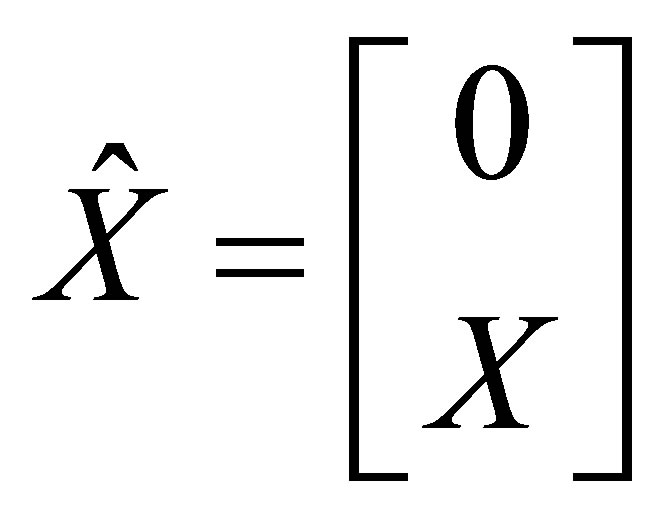 , we obtain
, we obtain
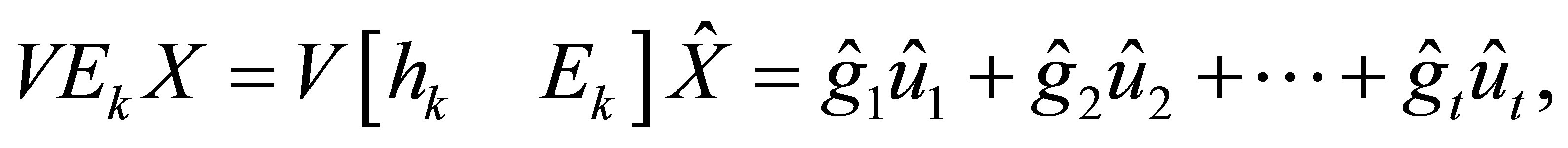 (3.5)
(3.5)
where  is the polynomial with degree
is the polynomial with degree 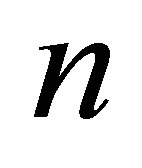 which is generated by the subvector of
which is generated by the subvector of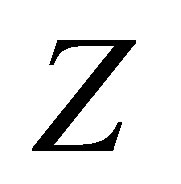 :
:

 is the polynomial with degree
is the polynomial with degree  which is generated by the subvector of
which is generated by the subvector of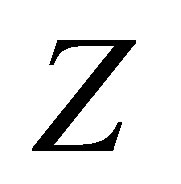 :
:
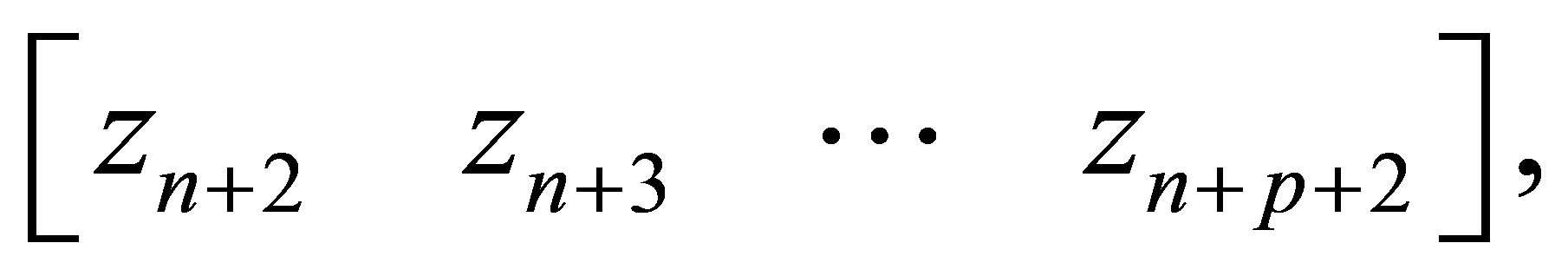

 is the polynomial with degree
is the polynomial with degree 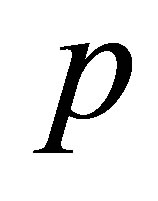 which is generated by the subvector of
which is generated by the subvector of :
:

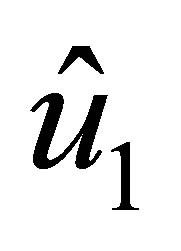 is the polynomial with degree
is the polynomial with degree 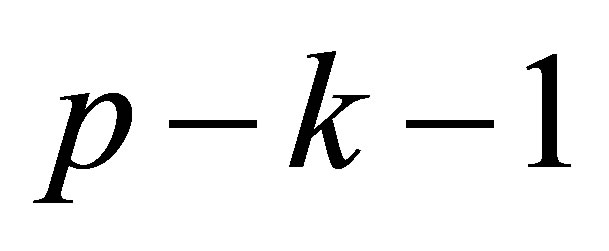 which is generated by the subvector of
which is generated by the subvector of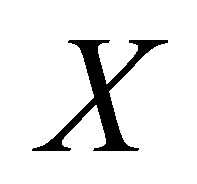 :
:

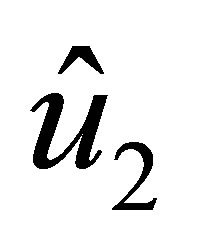 is the polynomial with degree
is the polynomial with degree 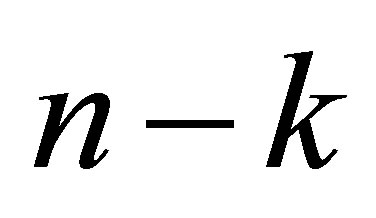 which is generated by the subvector of
which is generated by the subvector of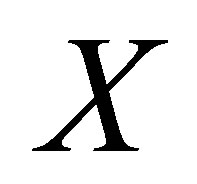 :
:
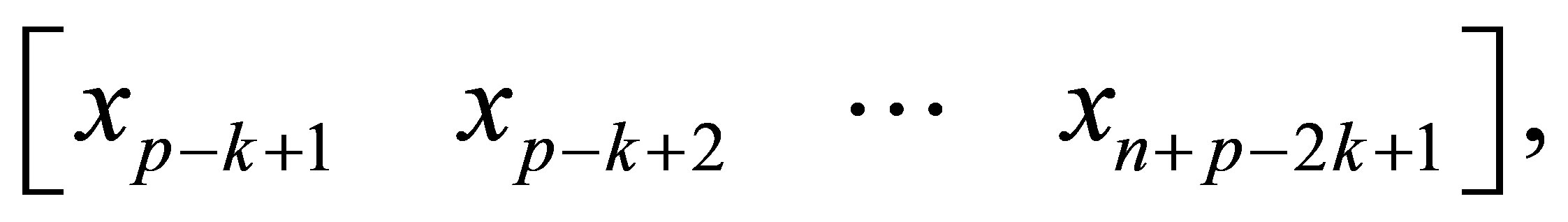

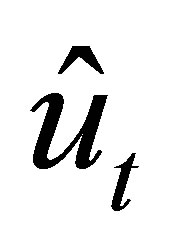 is the polynomial with degree
is the polynomial with degree 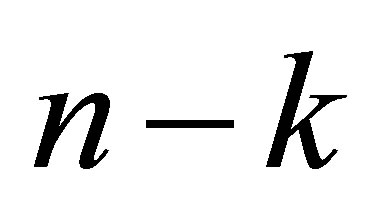 which is generated by the subvector of
which is generated by the subvector of :
:
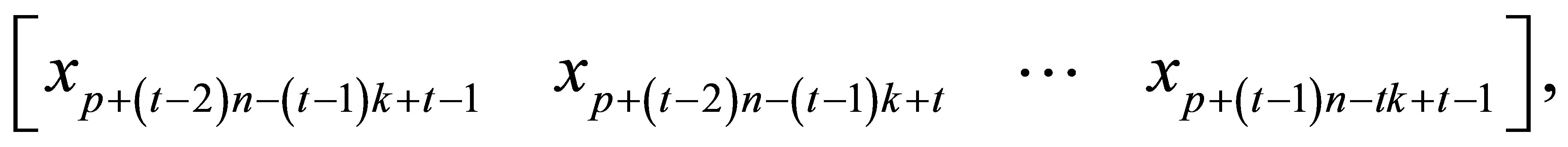
Here we will present a simple example to illustrate how to find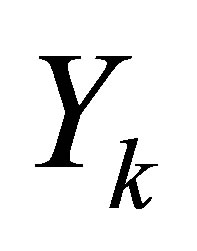 .
.
Example 3.1. Suppose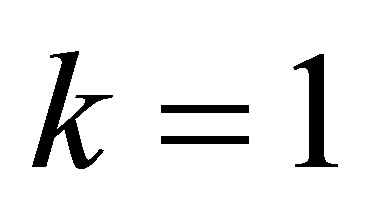 ,
, 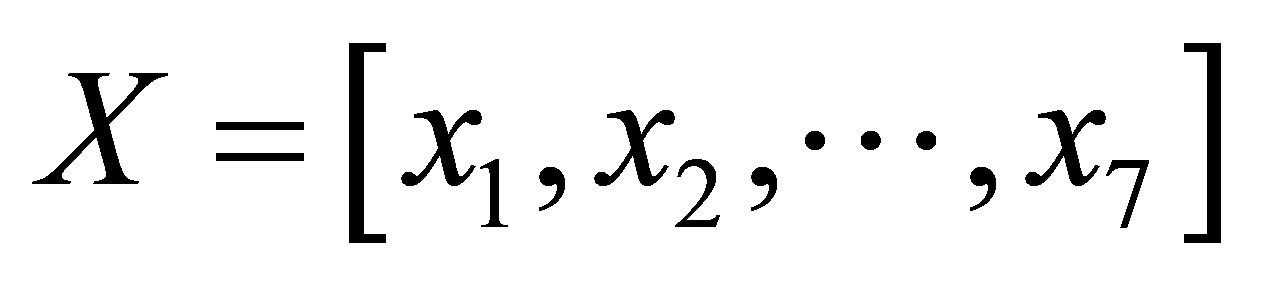 and
and 
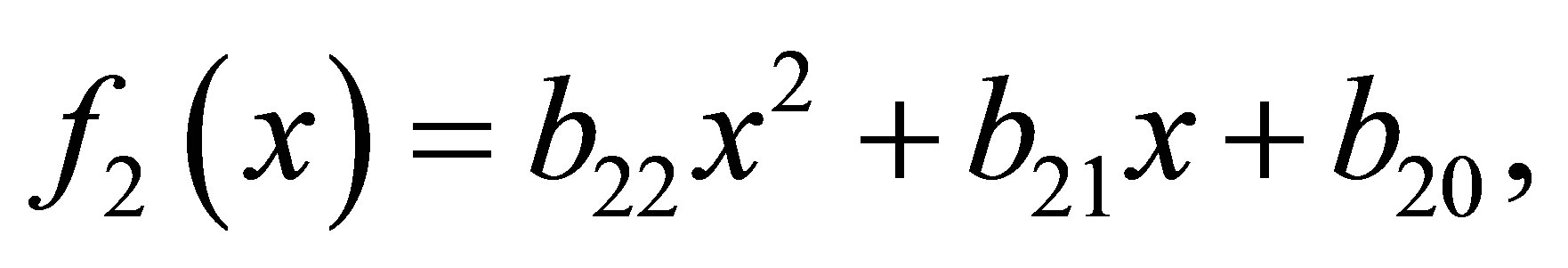
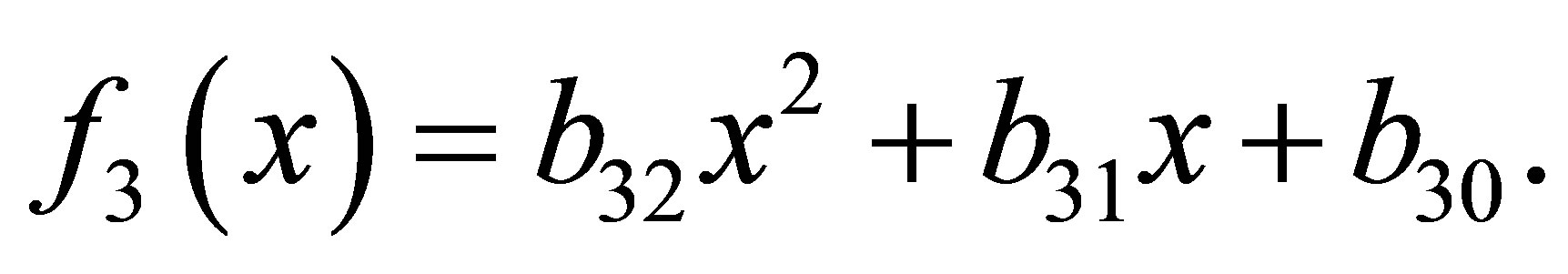
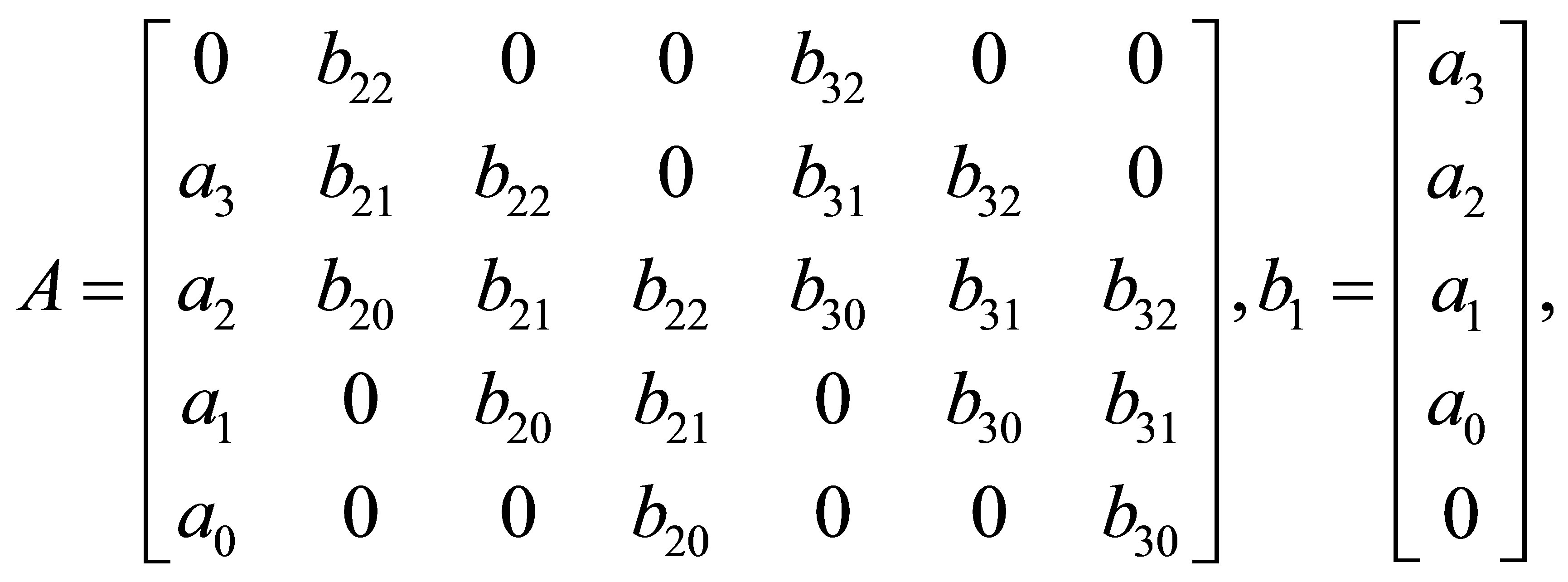
then
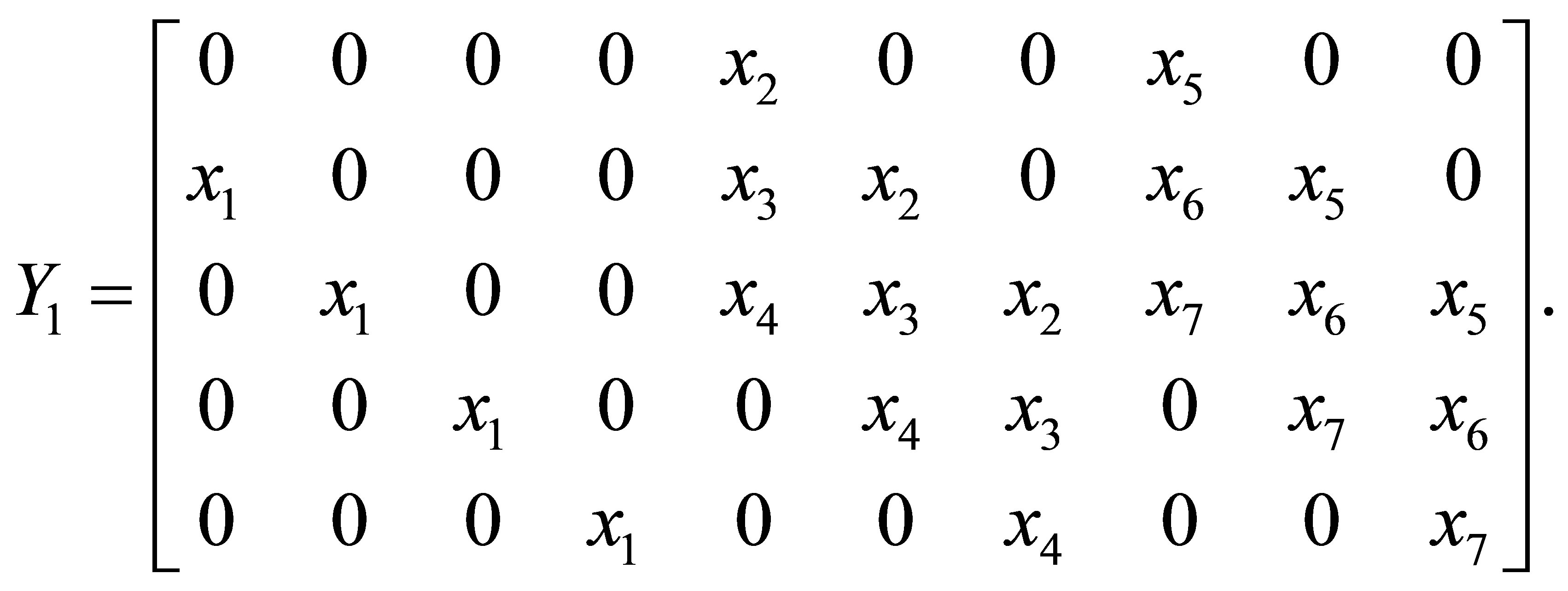
4. Approximate GCD Algorithm and Experiments
The following algorithm is designed to solve Problem 1.1.
Algorithm 4.1.
Input-A Sylvester matrix S generated by 
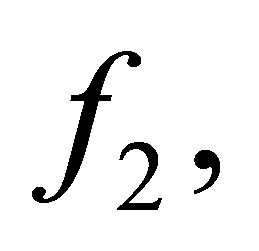

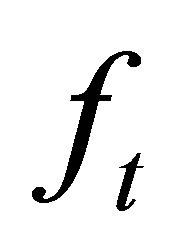 , respectively, an integer
, respectively, an integer 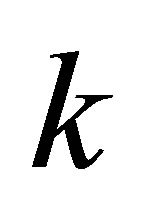 and a tolerance
and a tolerance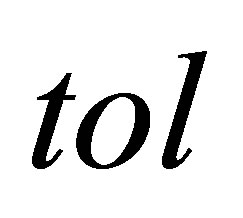 .
.
Output-Polynomials 


 and the Euclidean distance
and the Euclidean distance 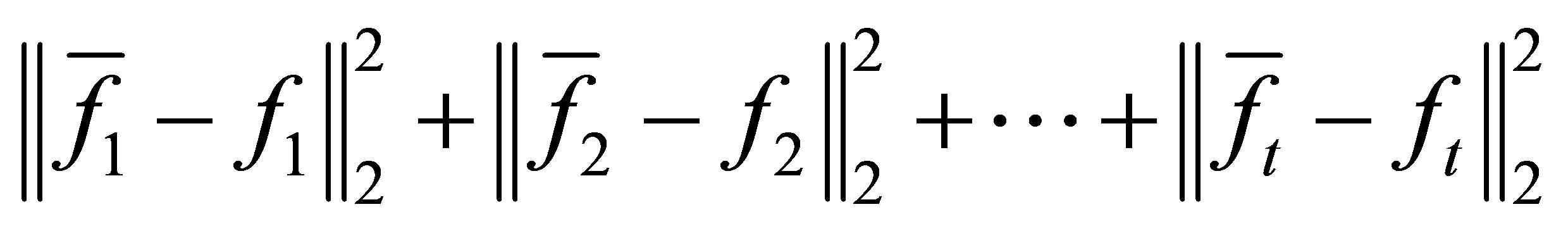 is to a minimum.
is to a minimum.
1) Form the 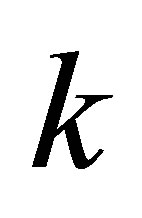 -th Sylvester matrix
-th Sylvester matrix 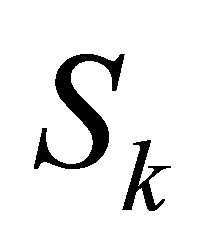 as the above section, set the first column of
as the above section, set the first column of 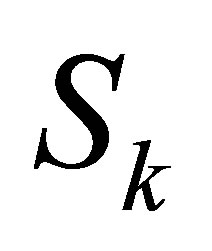 as
as  and the remainder columns of
and the remainder columns of 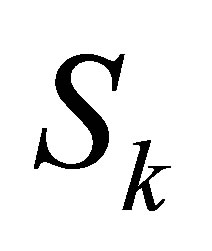 as
as . Let
. Let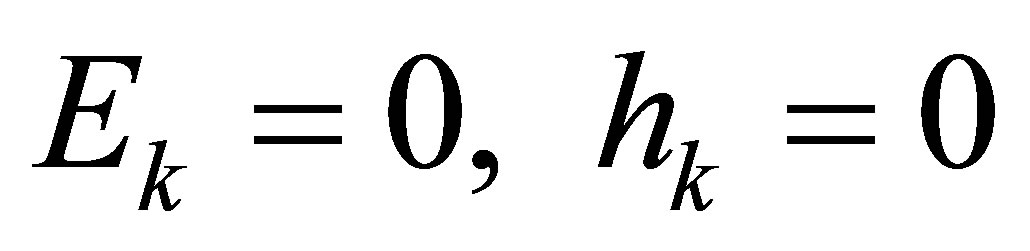 .
.
2) Calculate 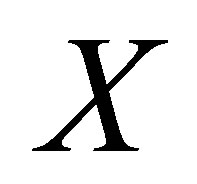 from
from 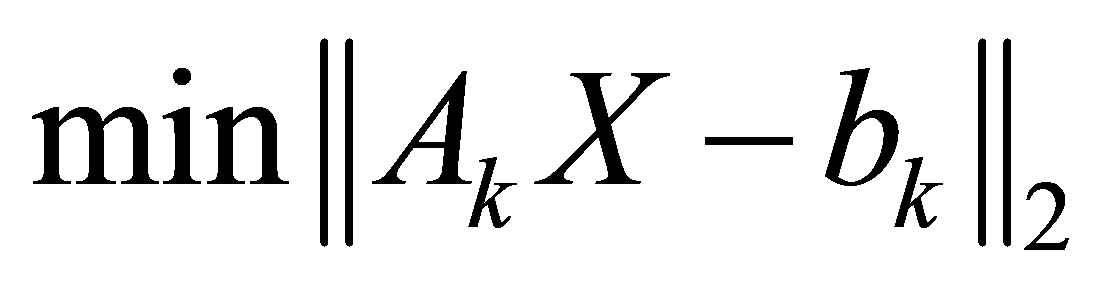 and
and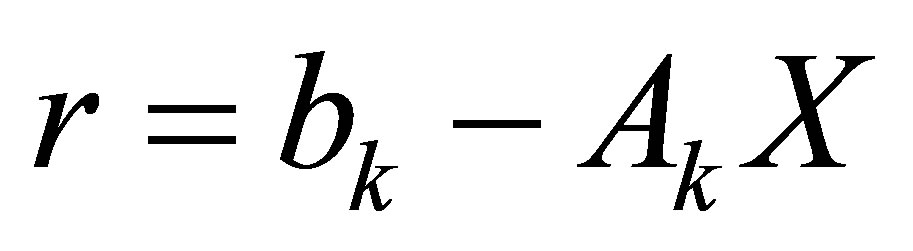 . Compute
. Compute 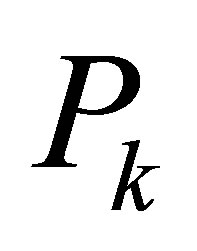 and
and 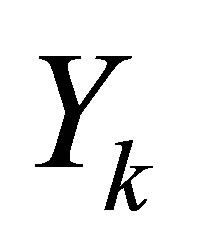 as the above section.
as the above section.
3) Repeat
(1) 
(2) Let 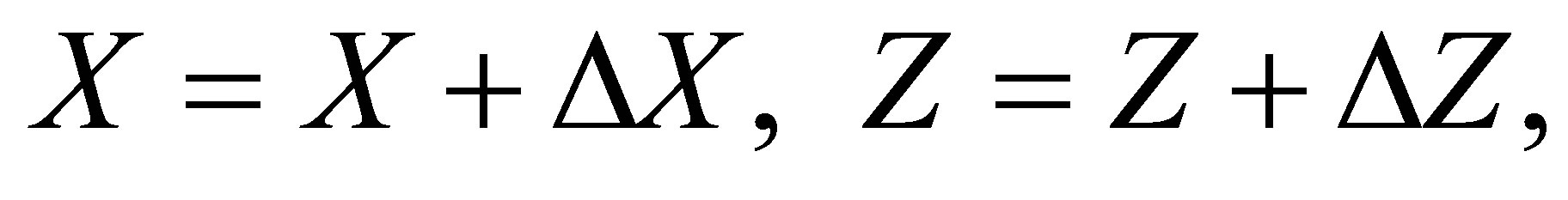
(3) Form the matrix 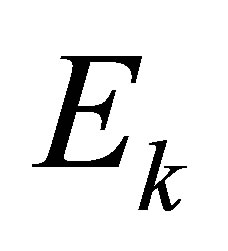 and
and  from
from , and
, and 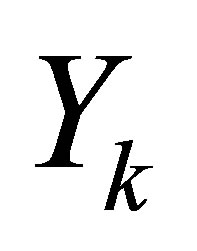 from
from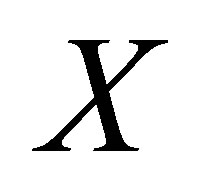 . Let
. Let 

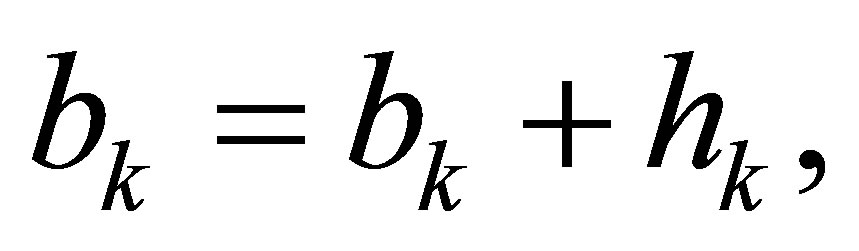 until
until  and
and 
4) Output the polynomials 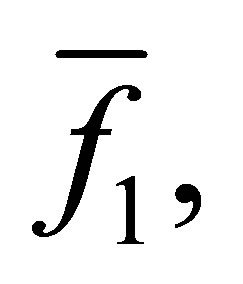


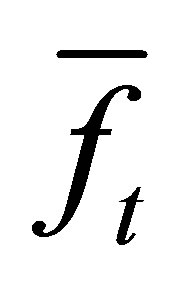 constructed from
constructed from 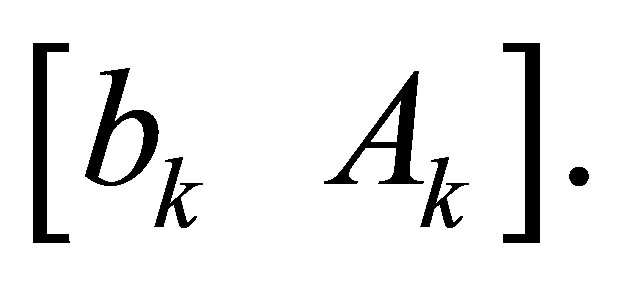
Given a tolerance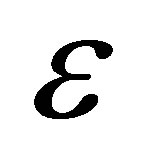 , we can use the Algorithm 4.1 to compute an approximate GCD of
, we can use the Algorithm 4.1 to compute an approximate GCD of . The method begin with
. The method begin with  using Algorithm 4.1 to compute the minimum perturbation
using Algorithm 4.1 to compute the minimum perturbation 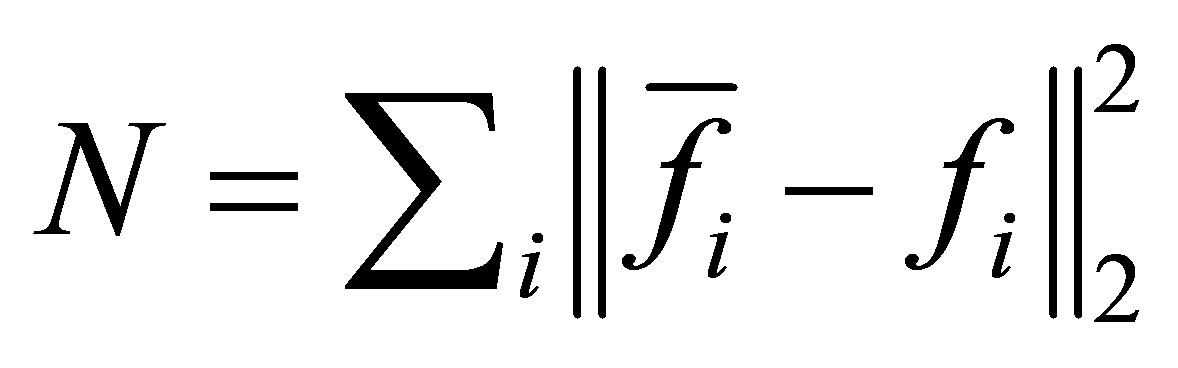
with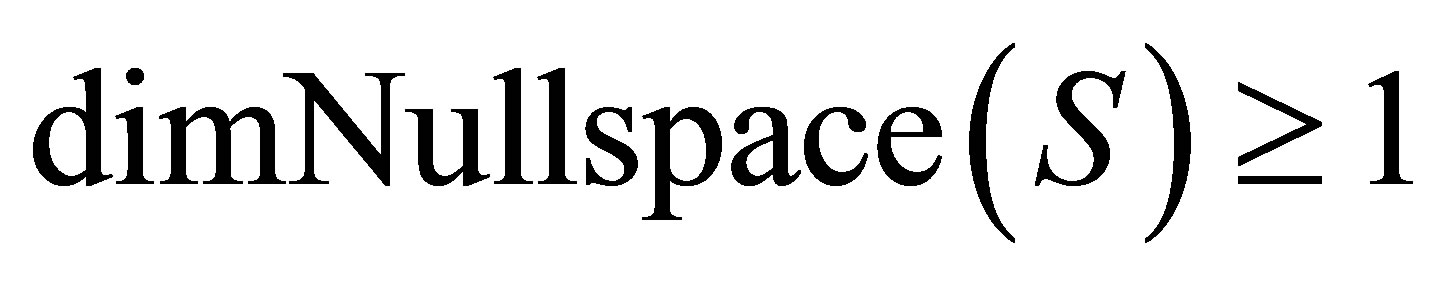 . If
. If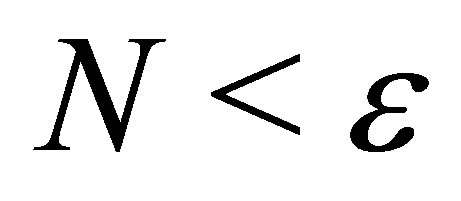 , then we can compute the approximate GCD form matrix
, then we can compute the approximate GCD form matrix . Otherwise, we reduce
. Otherwise, we reduce 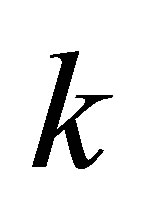 by one and repeat the Algorithm 4.1.
by one and repeat the Algorithm 4.1.
Example 4.1. We wish to find the minimal polynomial perturbations  and
and  of
of
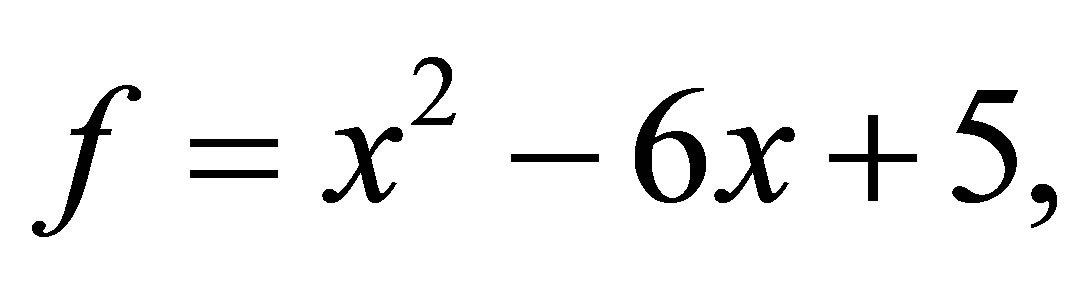
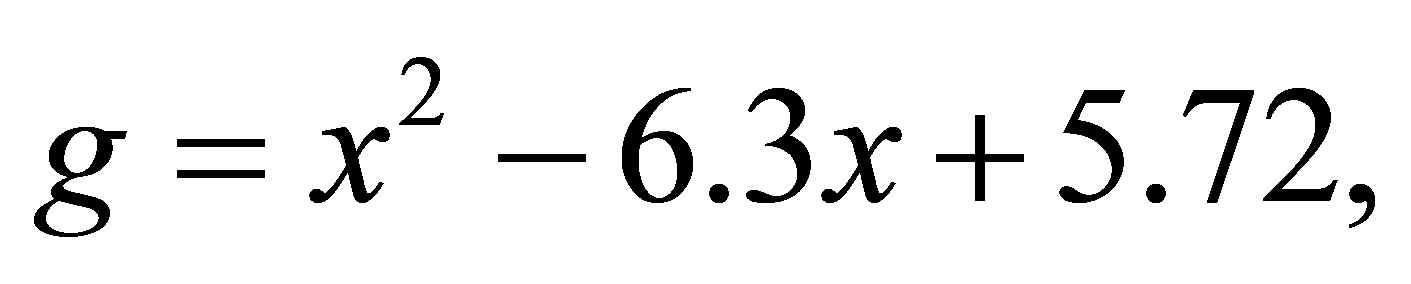
satisfy that the polynomials  and
and 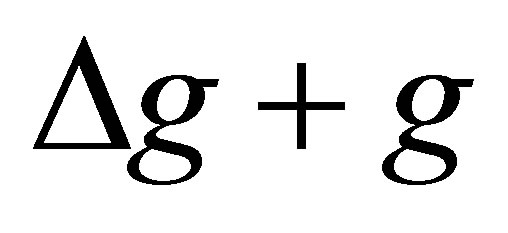 have a common root. We take two cases into account.
have a common root. We take two cases into account.
Case 1: The leading coefficients can be perturbed. Let 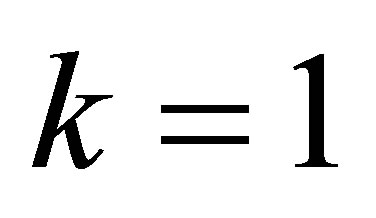 and
and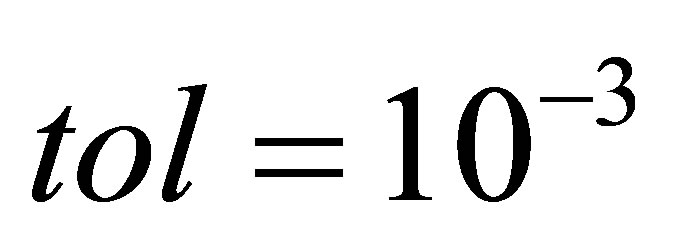 , after 3 iterations, we get the polynomials
, after 3 iterations, we get the polynomials  and
and 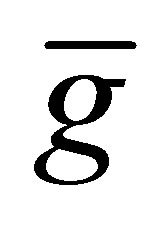


with a minimum distance

Case 2: The leading coefficients can be perturbed. Let  and
and , after 3 iterations, we have the polynomials
, after 3 iterations, we have the polynomials  and
and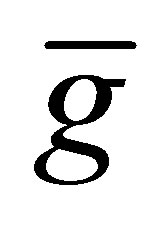 :
:
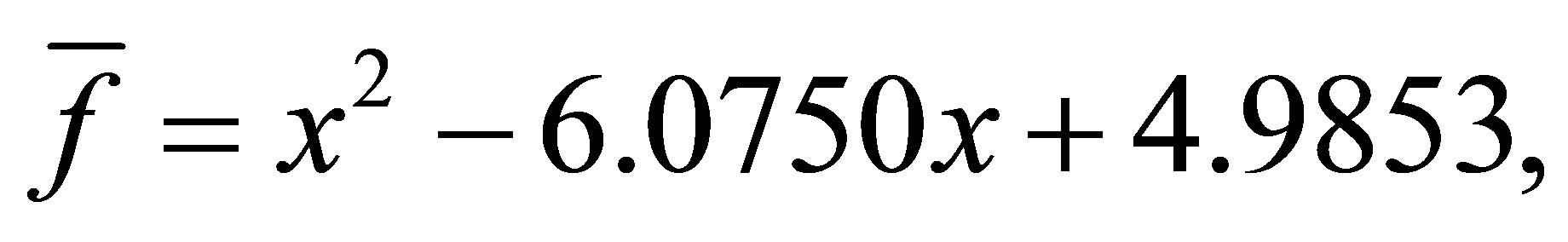

with a minimum distance

Example 4.2. Let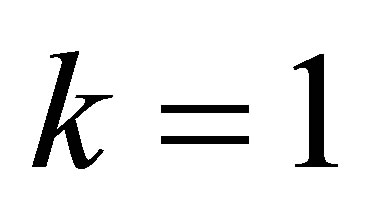 ,
,  and
and
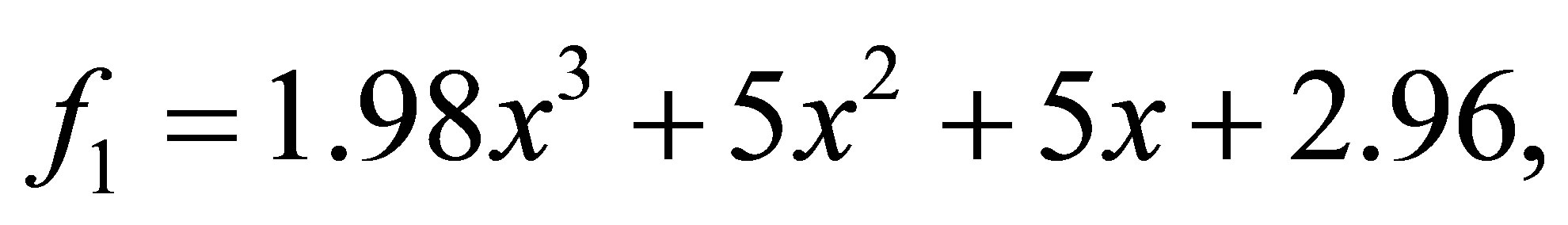
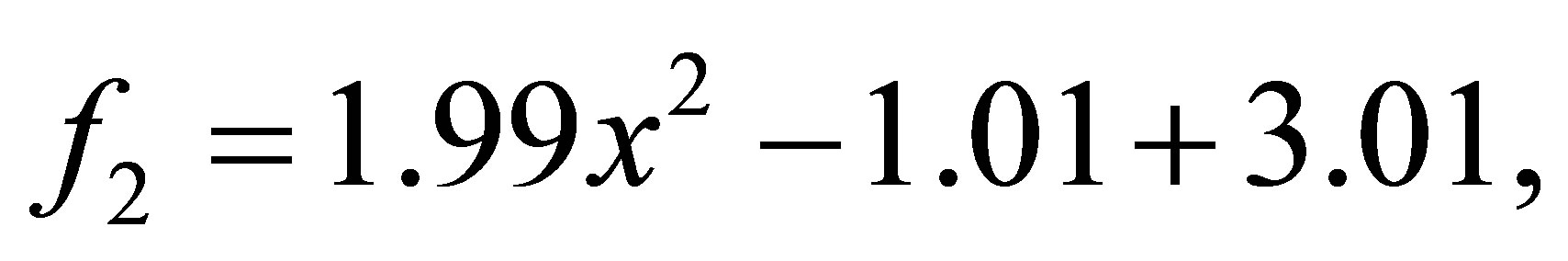
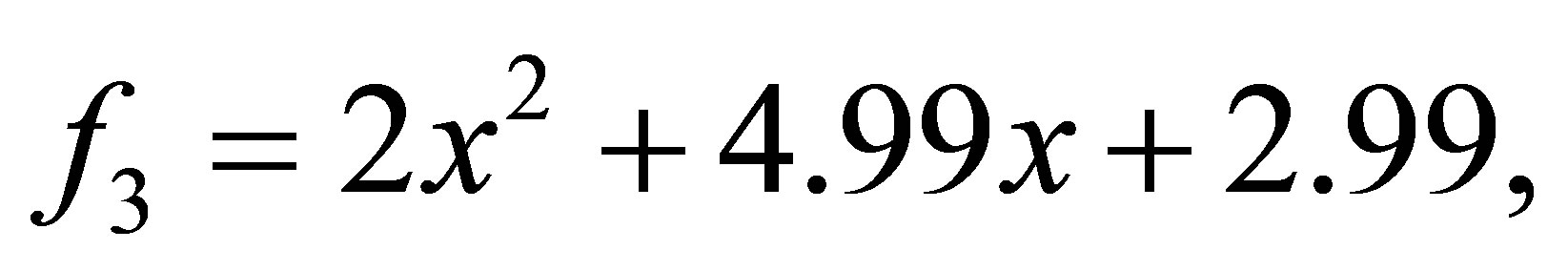
after 8 iterations, we have the polynomials
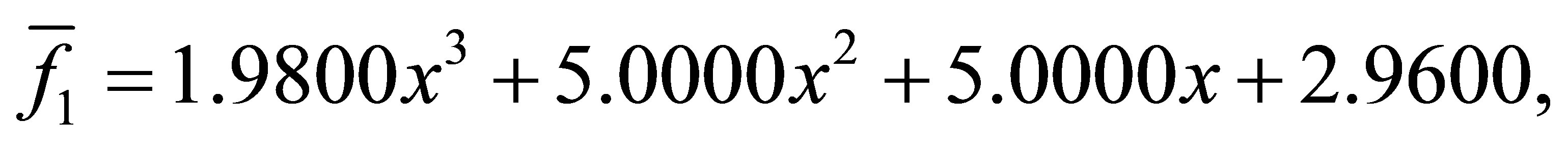


with a minimum distance

and the CPU time
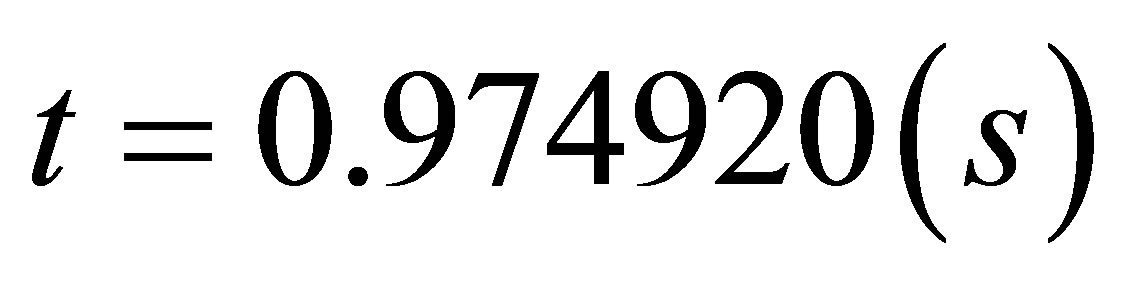
Example 4.3. Let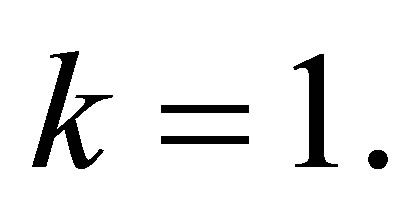 ,
, 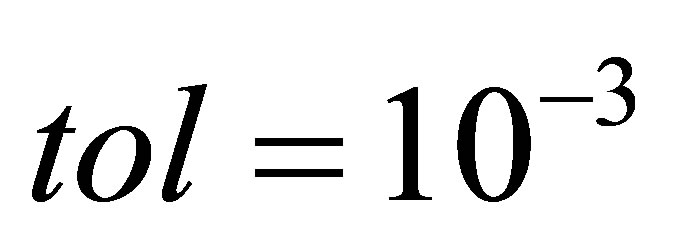 and
and
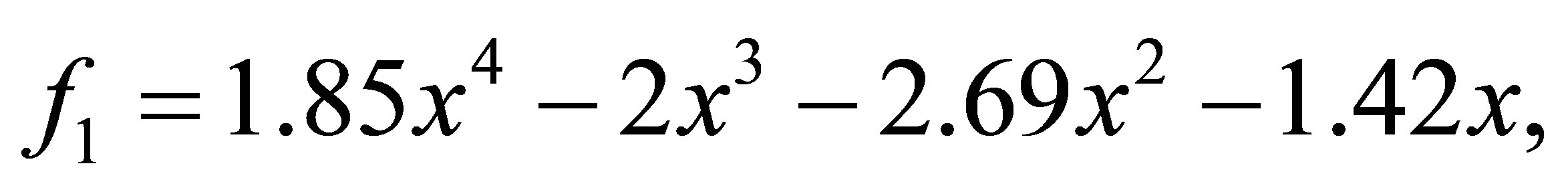



after 11 iterations, we have the polynomials
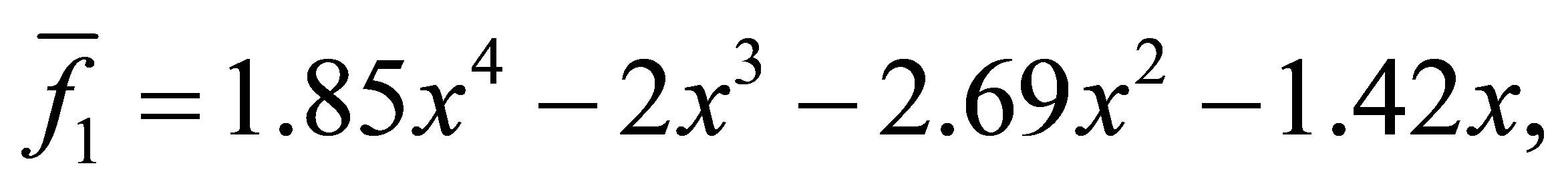

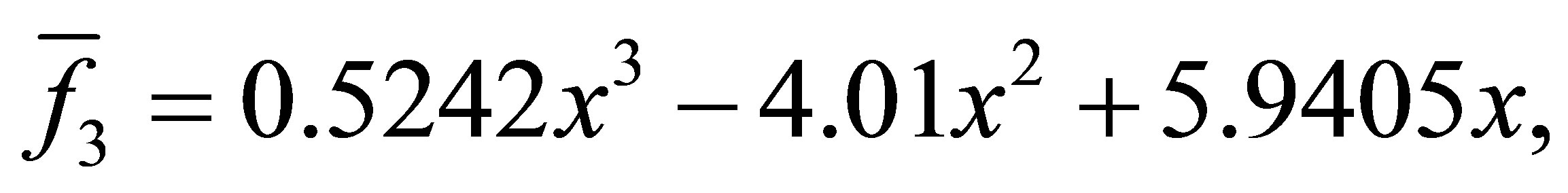

with a minimum distance
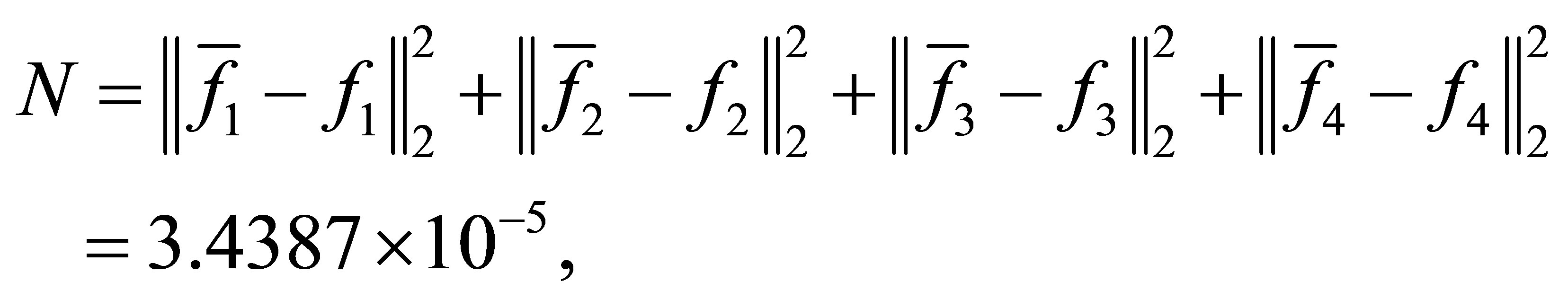
and the CPU time
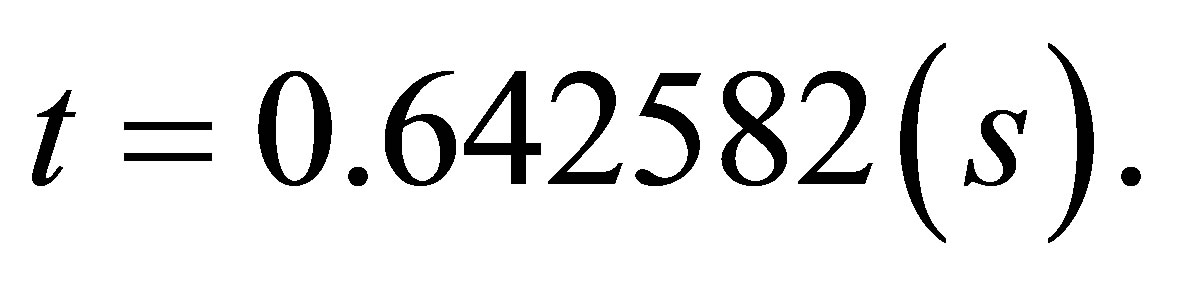
Example 4.4. Let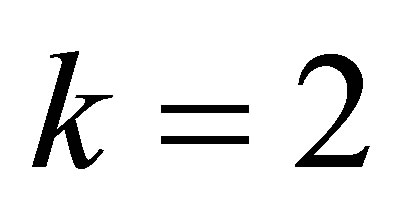 ,
,  and
and
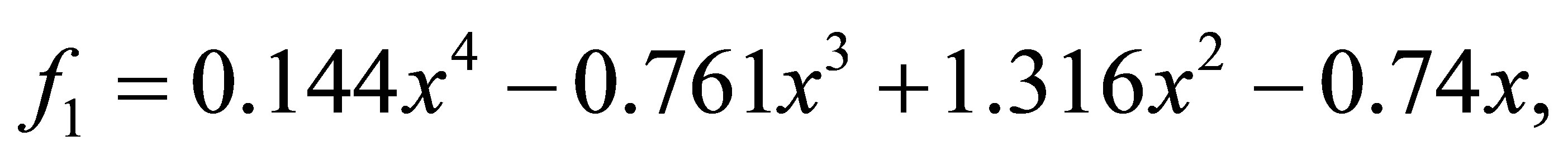


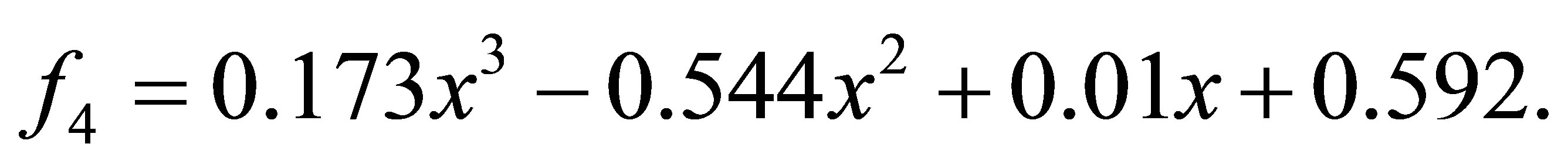
after 1 iteration, we have the polynomials


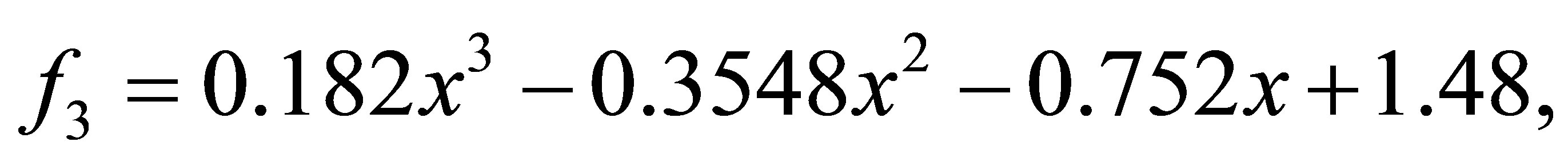
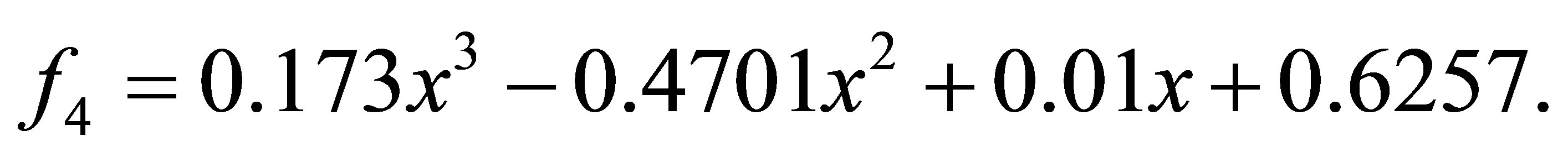
with a minimum distance
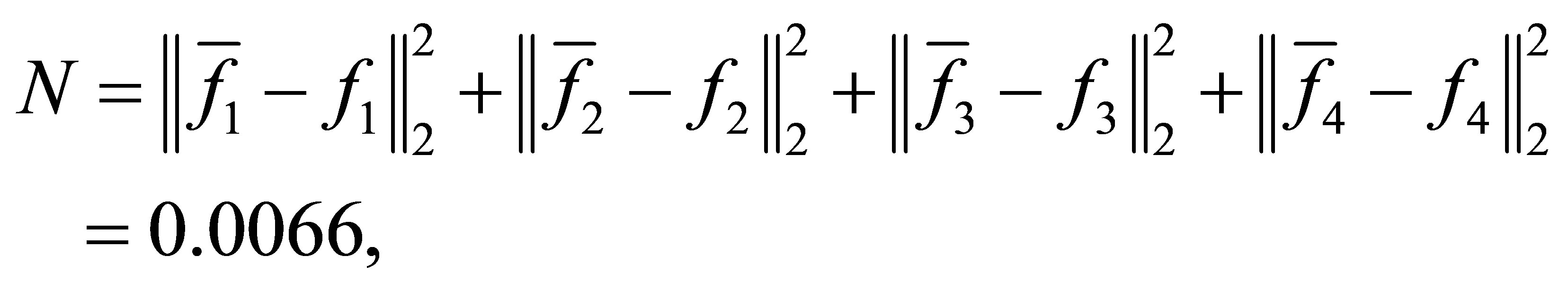
and the CPU time
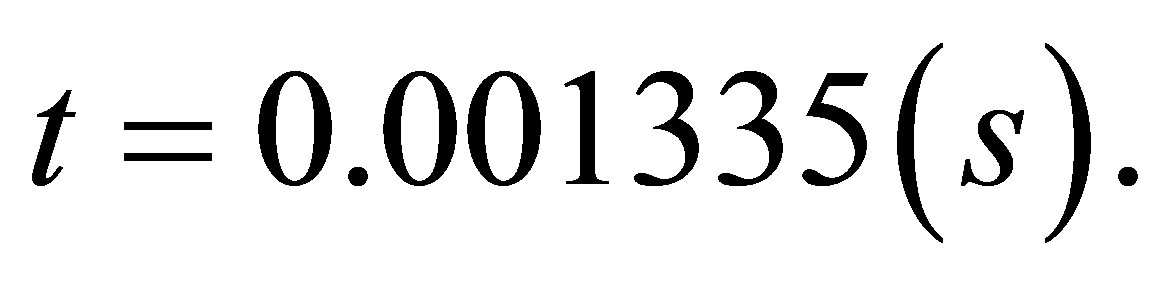
Example 4.5. Let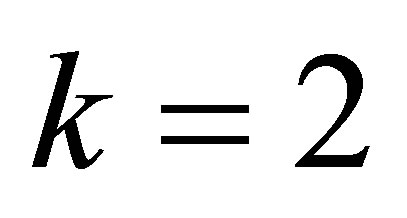 ,
, 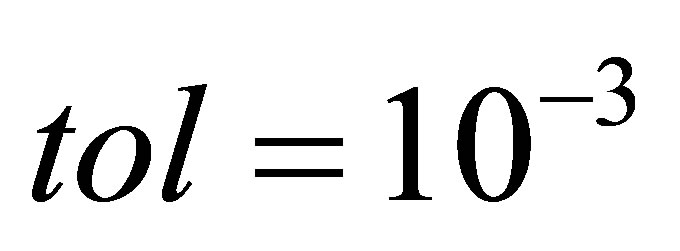 and
and


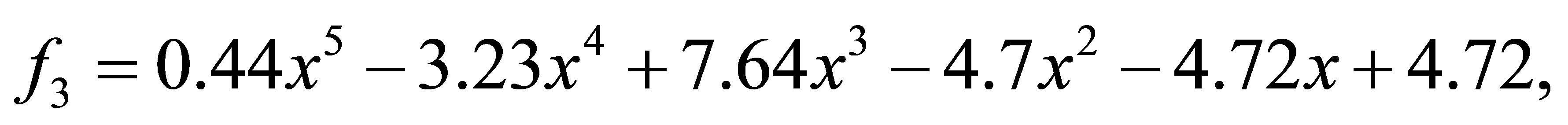
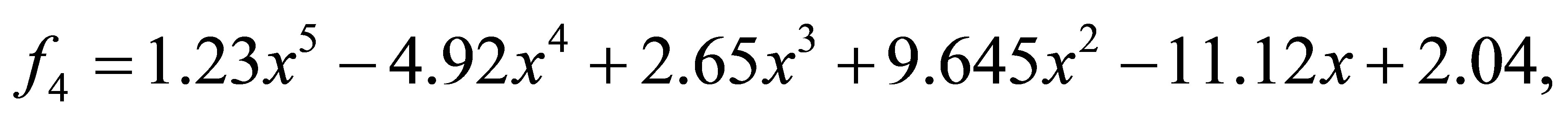
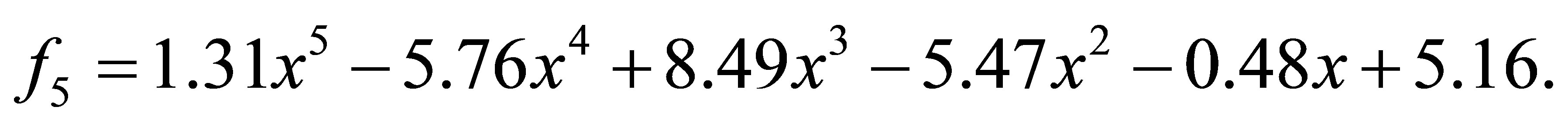
after 1 iteration, we have the polynomials

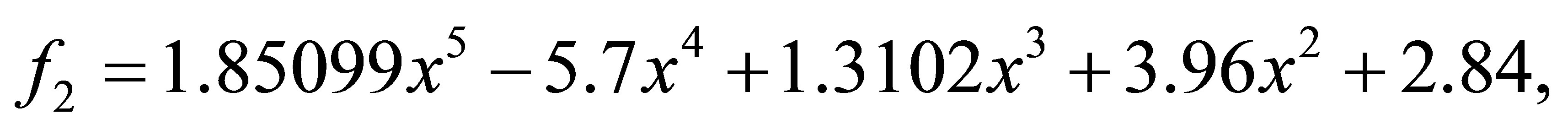
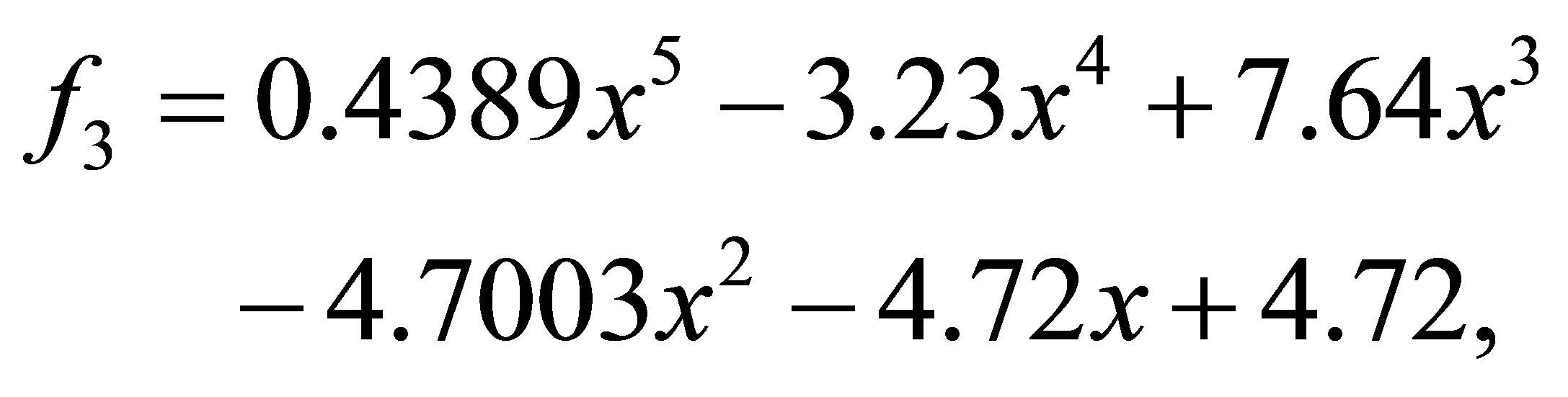
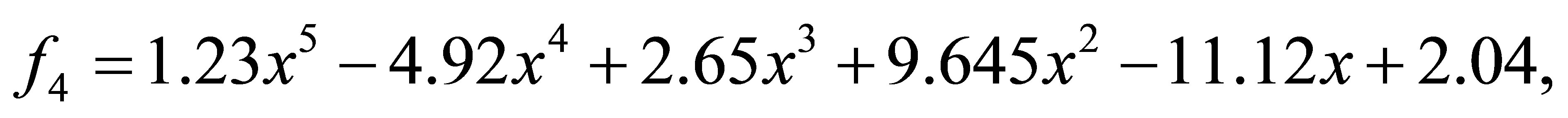

with a minimum distance
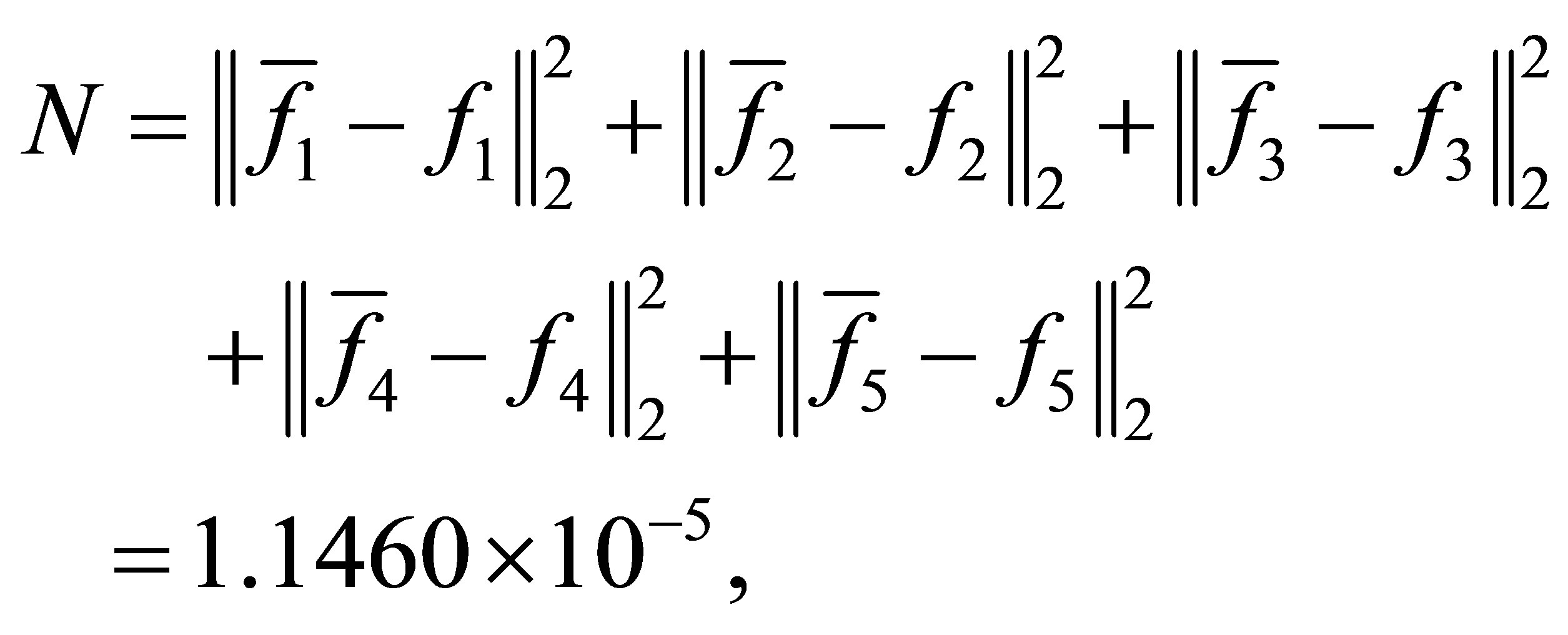
and the CPU time
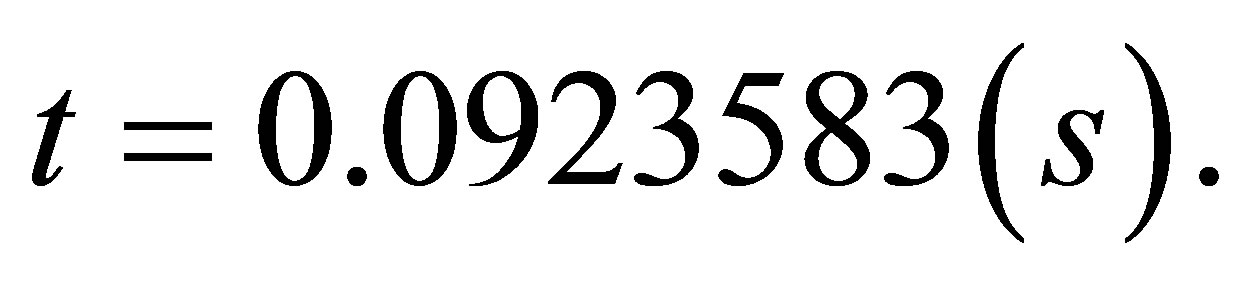
Examples 4.1, 4.2, 4.3, 4.4 and 4.5 show that Algorithm 4.1 is feasible to solve Problem 1.1.
In Table 1, we present the performance of Algorithm 4.1 and compare the accuracy of the new fast algorithm with the algorithms in [9,21]. Denote 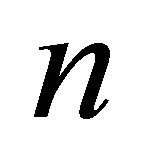 be the total degree of polynomials
be the total degree of polynomials  and
and  be the total degree of polynomials
be the total degree of polynomials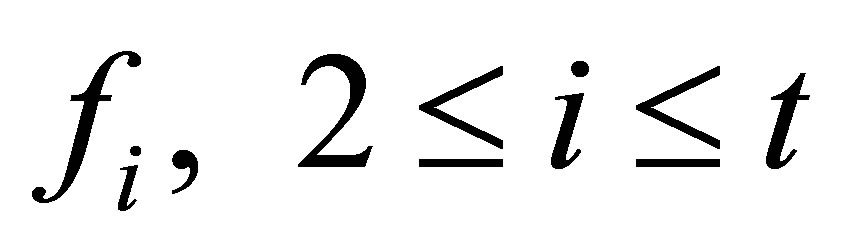 . It (Chu) stands for the number of iterations by the method in [14] whereas it (STLN) denotes the number of iterations by Algorithm 4.1. Denoted by error(Zeng) and error (STLN) are the perturbations
. It (Chu) stands for the number of iterations by the method in [14] whereas it (STLN) denotes the number of iterations by Algorithm 4.1. Denoted by error(Zeng) and error (STLN) are the perturbations 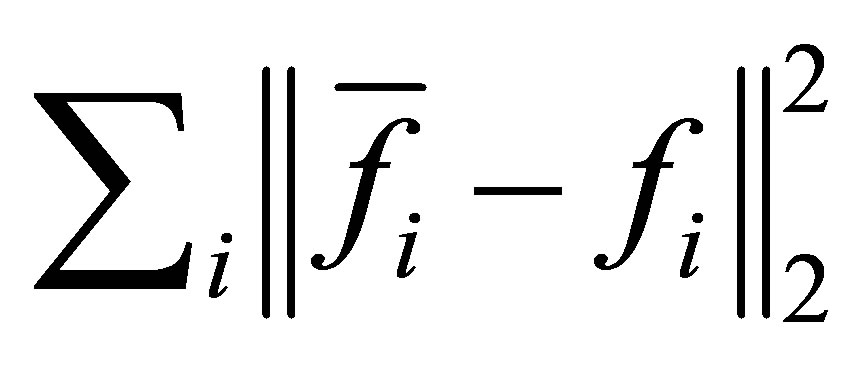 computed by the method in
computed by the method in
[21] and Algorithm 4.1, respectively. The last two columns denote the CPU time in seconds costed by AFMP algorithm and our algorithm, respectively.
As shown in the above table, we show that our method based on STLN algorithm converges quickly to the minimal approximate solutions, needing no more than 2 iterations whereas the method in [14] requires more iteration steps. We also note that our algorithm still converges very quickly when the degrees of polynomials become large while the algorithm in [14] needs more iteration steps. Besides, our algorithm needs less CPU time than the AFMP algorithm. So the convergence speed of our method is faster. From the errors, we demonstrate that our method has smaller magnitudes compared with the method in [21]. So our algorithm can generate much more accurate solutions.
5. Conclusion
In this paper, we present that approximation GCD of several polynomials can be solved by a practical and reliable way based on STLN method and transformed to the approximation of Sylvester structure problem. For the matrices related to the minimization problems are all structured matrix with low displacement rank, applying the algorithm to solve these minimization problems would be possible. The complexity of the algorithm is reduced with respect to the degrees of the given polynomials. Although the problem of structured low rank ap-

Table 1. Algorithm performance on benchmarks.
proximation has been studied in many literatures and obtained many accomplishments, there is still much work to be done, for example, low rank approximation of finite dimensional matrix has not been fully resolved.
NOTES