1. Introduction
In the present paper we study the following natural question: does there exist a weighted space , with
, with , such that for every function in the space
, such that for every function in the space

one can find a series in the Walsh generalized system  of the form
of the form

that possess the following property: for any function  there exists a growing sequence of natural numbers
there exists a growing sequence of natural numbers  such that the subseries
such that the subseries  converges to
converges to  in the
in the  norm and a.e.
norm and a.e.
Note that the problem of representing a function  by a series in classical and general orthonormal systems has a long history. Of course the problem of the representation of functions was studied before Luzin’s work. It goes back to D. Bernoulli, L. Euler and many others.
by a series in classical and general orthonormal systems has a long history. Of course the problem of the representation of functions was studied before Luzin’s work. It goes back to D. Bernoulli, L. Euler and many others.
A question posed by Lusin in 1915 asks whether it is possible to find for every measurable function 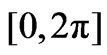 a trigonometric series, with coefficient sequence converging to zero, that converges to the function almost everywhere. For real-valued functions, this question was given an affirmative answer by Men’shov [1] in 1941.
a trigonometric series, with coefficient sequence converging to zero, that converges to the function almost everywhere. For real-valued functions, this question was given an affirmative answer by Men’shov [1] in 1941.
There are many other works (see [2-11]) devoted to representations of functions by series in classical and general orthonormal systems and the existence of different types of universal series in the sense of convergence almost is everywhere and by measure.
Since the trigonometric and Walsh systems have many properties in common, one would think that there should be a corresponding result for the Walsh system. This is, indeed, the case, and, in fact, the same sort of result holding for a multitude of Walsh subsystems, many of them are quite sparse and far from complete.
In this paper we prove the following theorem:
Theorem 1. For any 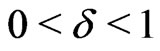 there exists a measurable function
there exists a measurable function 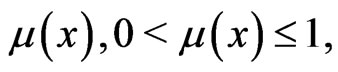 with
with
 such that for any
such that for any  and any function
and any function  there exists a series in the Walsh generalized system
there exists a series in the Walsh generalized system  of the following form
of the following form
 (1)
(1)
which converges to 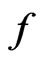 in the
in the —metric and almost everywhere.
—metric and almost everywhere.
Note that there exist functions in the space  that can not be represented by series in the Walsh system
that can not be represented by series in the Walsh system  (see [8], pp. 124-125).
(see [8], pp. 124-125).
Theorem 1 is a consequence of the more general Theorem 2, which is stated as follows:
Theorem 2. For any  there exists a measurable function
there exists a measurable function  with
with
 and a series in the Walsh generalized system
and a series in the Walsh generalized system  of the form
of the form

that possess the following property: for any function  there exists a growing sequence of natural numbers
there exists a growing sequence of natural numbers  such that the subseries
such that the subseries

converges to  in the
in the  -norm and a.e.
-norm and a.e.
Recall the following definition: a series  is said to be universal with respect to subseries in the space
is said to be universal with respect to subseries in the space , if for each function
, if for each function , one can select a subseries
, one can select a subseries  which converges to
which converges to  in
in  norm .
norm .
The above-mentioned definitions are given not in the most general form and only in the generality, in which they will be applied in the present paper.
Note that the result of the Theorem 2 is definitive in a certain sense: one can not replace 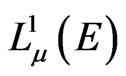 by
by  because no orthonormal system of bounded functions does there exist a series universal in
because no orthonormal system of bounded functions does there exist a series universal in  with respect to subseries. This is almost obvious.
with respect to subseries. This is almost obvious.
The following problems remain open.
Question 1. Are the theorems 1 and 2 true for the trigonometric system?
Question 2. What kind of necessary and sufficient conditions should be imposed on the weight function  in order to construct a Walsh series
in order to construct a Walsh series 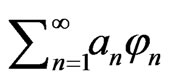 to be universal in the space with respect to subseries?
to be universal in the space with respect to subseries?
2. Proofs of Main Lemmas
Let  be a fixed integer and
be a fixed integer and . Recall the following definitions.
. Recall the following definitions.
The Rademacher system of order  is defined inductively as follows. For
is defined inductively as follows. For  let
let

and for  let
let

The Walsh generalized system (see [3] and [13,14]) of order 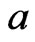 is defined by
is defined by

and if , where
, where ,
,  then
then
 .
.
We denote the generalized Walsh system of order  by
by . Note that
. Note that  is the classical Walsh system. The basic properties of the generalized Walsh system of order
is the classical Walsh system. The basic properties of the generalized Walsh system of order  have been obtained by H. E. Chrestenson, J. Fine, C. Vateri, W. Young, N. Vilenkin and others. Next we list some properties of
have been obtained by H. E. Chrestenson, J. Fine, C. Vateri, W. Young, N. Vilenkin and others. Next we list some properties of , which will be useful later.
, which will be useful later.
• Each 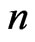 -th Rademacher function has period
-th Rademacher function has period .
.
•  ,
,  , and
, and  (mod
(mod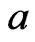 ).
).
•  is a finite product of Rademacher functions with values in
is a finite product of Rademacher functions with values in .
.
•  if
if .
.
•  ,
,  is a complete orthonormal system in
is a complete orthonormal system in
 and it is basic in
and it is basic in  for
for .
.
We put
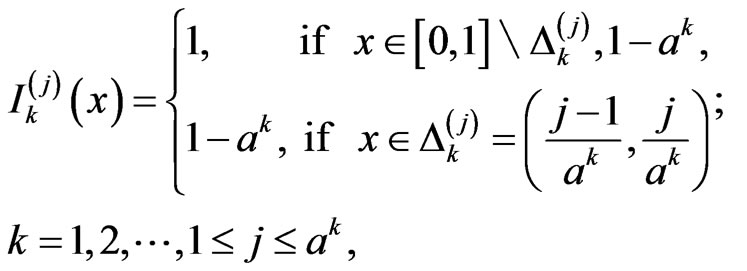 (2)
(2)
and periodically extend these functions on  with period 1.
with period 1.
By  we denote the characteristic function of the set
we denote the characteristic function of the set , i.e.
, i.e.
 (3)
(3)
Then, clearly
 (4)
(4)
and let for the natural numbers 
 (5)
(5)
 (6)
(6)
Hence
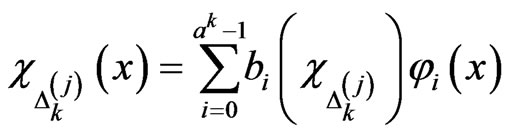 (7)
(7)
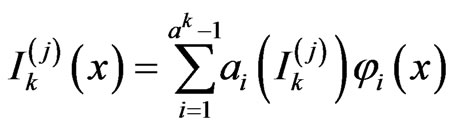 . (8)
. (8)
Lemma 1. Let dyadic interval

and numbers  be given. Then there exists a measurable set
be given. Then there exists a measurable set  and a polynomial
and a polynomial 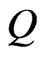 in the Walsh generalized system
in the Walsh generalized system  of the following form
of the following form

which satisfy the following conditions:
1) the coefficients  are
are  or
or 2)
2) 3)
3) 4)
4) 
where 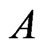 is a constant5)
is a constant5) .
.
Proof. Let
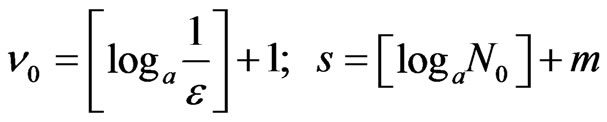 (9)
(9)
We define the polynomial  and the numbers
and the numbers ,
,  and
and  in the following form:
in the following form:
 (10)
(10)
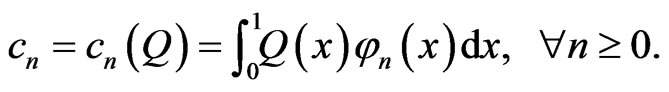 (11)
(11)
 (12)
(12)
Taking into consideration the following equation

and having the following relations (5)-(8) and (10)-(12), we obtain that the polynomial  has the following form:
has the following form:
 (13)
(13)
where
 (14)
(14)
Then let

Clearly that (see (2) and (10)),
 (15)
(15)
 (16)
(16)

Hence

where  Repeating the arguments in the proof of Lemma 1, we get a proof of the last statement of Lemma 1. Lemma 1 is proved.
Repeating the arguments in the proof of Lemma 1, we get a proof of the last statement of Lemma 1. Lemma 1 is proved.
Lemma 2. Let given the numbers . Then for any function
. Then for any function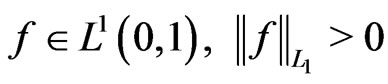 , one can find a set
, one can find a set  and a polynomial in the Walsh generalized system
and a polynomial in the Walsh generalized system

satisfying the following conditions:

 and the non-zero coefficients in
and the non-zero coefficients in
 are in decreasing order2)
are in decreasing order2) 3)
3) 
4) for every measurable subset e of E5)
for every measurable subset e of E5) .
.
Proof. We choose some non-overlapping binary intervals 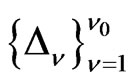 and a step function
and a step function
 (17)
(17)
satisfying the conditions
 (18)
(18)
 (19)
(19)
 (20)
(20)
Successively applying Lemma 1, we determine some sets 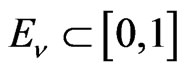 and polynomials
and polynomials
 (21)
(21)
where 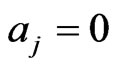 or
or , if
, if ,
,
 (22)
(22)
 , (23)
, (23)
 , (24)
, (24)
Then let
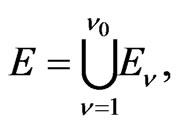 (25)
(25)
 (26)
(26)
>From (19), (21), (22) and (25) follows, that
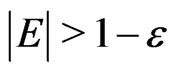
and 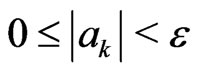 and the non-zero coefficients in
and the non-zero coefficients in  are in decreasing order, i.e. the statements 1) - 3) of Lemma 2 are valid.
are in decreasing order, i.e. the statements 1) - 3) of Lemma 2 are valid.
To verify the statement 4), for any  determine
determine  from the condition
from the condition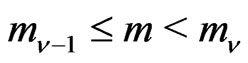 . Then by (21) and (26)
. Then by (21) and (26)
 (27)
(27)
Since for any point ,
,  (see (17), (23) and (26)), then from the conditions (18), (24), and (27) for every measurable subset e of E.
(see (17), (23) and (26)), then from the conditions (18), (24), and (27) for every measurable subset e of E.
We have
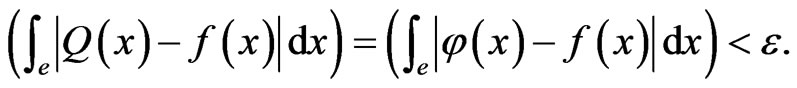

Repeating the arguments in the proof of Lemma 2, we get a proof of the last statement of Lemma 2. Lemma 2 is proved.
The main tool in the proof of Theorem 2 is the following result.
Lemma 3. Let  the Walsh generalized system, then for any
the Walsh generalized system, then for any  there exist a weight function
there exist a weight function
 with
with 
such that for any numbers 
 , and evry function
, and evry function , one can find polynomial in the Walsh generalized system
, one can find polynomial in the Walsh generalized system

satisfying the following conditions:

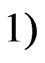 2)
2) 
3)
 .
.
Proof of Lemma 3
Let
 (28)
(28)
be the sequence of all algebraic polynomials with rational coefficients. Applying repeatedly Lemma 2, we obtain sequences of  sets and polynomials in the Walsh systems
sets and polynomials in the Walsh systems 
 (29)
(29)
where

which satisfy the following conditions:
 (30)
(30)
 (31)
(31)
 (32)
(32)
for every measurable subset e of 
 (33)
(33)
Setting
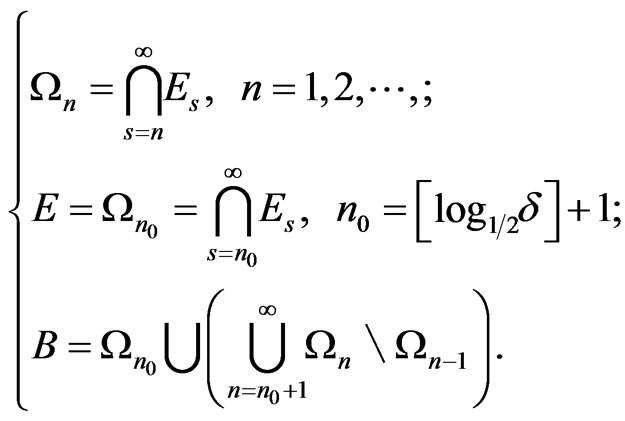 (34)
(34)
It is clear (see (33), (34))
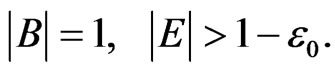
We define a function 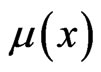 in the following way:
in the following way:
 (35)
(35)
where
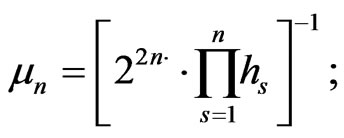 (36)
(36)

It follows from (34)-(36) that for all 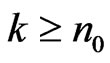
 (37)
(37)
In a similar way for all  we have
we have
 (38)
(38)
By the conditions (31), (35)-(38) for all 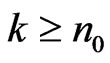 we obtain
we obtain
 (39)
(39)
Taking relations (32), (34)-(36) into account we obtain that for all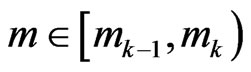 , and
, and 
 (40)
(40)
From the sequence (28) we choose a function  such that
such that
 (41)
(41)
 . (42)
. (42)
Then, we set
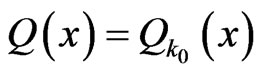 ,
, .
.
Now, it is not difficult to verify (see (30), (39)-(42)) that the function  and the polynomials
and the polynomials  satisfy the requirements of Lemma 3.
satisfy the requirements of Lemma 3.
Remark: In Lemma 3 polynom  can be chosen such that
can be chosen such that
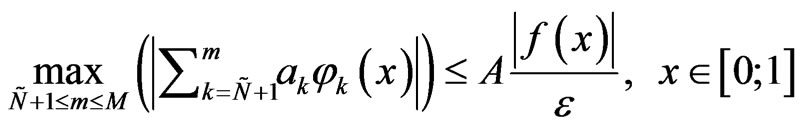
Lemma 3 is proved.
Proof Theorem 2
Let  and let
and let
 (43)
(43)
be the sequence of all algebraic polynomials with rational coefficients. Applying repeatedly Lemma 3, we obtain a weight function  with
with  and
and , a sequences of polynomials in the Walsh generalized systems
, a sequences of polynomials in the Walsh generalized systems 
 (44)
(44)
where

which satisfy the following conditions:
 (45)
(45)
 (46)
(46)
 (47)
(47)
Consider a series
 (48)
(48)
Clearly (see (45), (48))

let  and let
and let . We choose some
. We choose some  from sequence (43), to have
from sequence (43), to have

Suppose that the numbers  and polynomials
and polynomials  are already determined satisfying to the following conditions:
are already determined satisfying to the following conditions:
 (49)
(49)
 (50)
(50)
Let a function ,
,  be chosen from the sequence (43) such that
be chosen from the sequence (43) such that
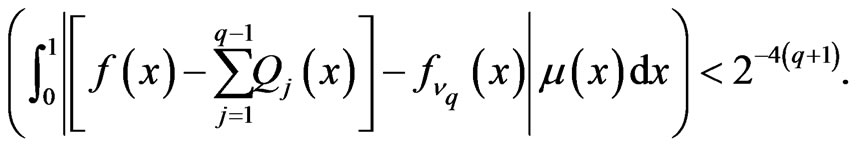 (51)
(51)
Hence by (49) we obtain
 (52)
(52)
From the conditions(46) (47), (52) follows that
 (53)
(53)
 (54)
(54)
Then we obtain that the series

where

converges to  in the
in the  -norm. Repeating the arguments in the proof of Theorem 2 and using Lemma 1, Lemma 2 and remark of Lemma 3 we get the proof of the second statement of Theorem 2.
-norm. Repeating the arguments in the proof of Theorem 2 and using Lemma 1, Lemma 2 and remark of Lemma 3 we get the proof of the second statement of Theorem 2.
Theorem 2 is proved.
NOTES