Bipolar Quantum Logic Gates and Quantum Cellular Combinatorics—A Logical Extension to Quantum Entanglement ()
1. Introduction
Aristotle’s causality principle denotes a necessary relationship between one event called cause and another event called effect which is the direct consequence of the cause. Without making clear the cause-effect relation any scientific theory can be said incomplete. But in more than 2300 years, all truth-based systems failed to provide logically definable causality with regularity. The dilemma was recognized and reiterated by a number of legendary figures, notably, by David Hume—a founder of modern empiricism who challenged Aristotle’s causality principle [1], Niels Bohr—a father figure of quantum mechanics who asserted that quantum causality is unattainable [2], and Lotfi Zadeh—founder of fuzzy logic who bluntly asserted that “Causality is undefinable” [3].
In quantum mechanics, Bell’s theorem [4] has been considered by many as a falsification of the EinsteinPodolsky-Rosen (EPR) argument [5]. It has led to a number of experiments that statistically support Bohr’s interpretation of quantum entanglement—the “spooky action in a distance” so-called by Einstein. But logically definable causality for quantum entanglement remains a mystery until today and the validity of Bell inequalities is still been questioned with experimental loopholes [6].
Niels Bohr was the first to bring YinYang into quantum theory for his particle-wave complementarity principle. When he was awarded the Order of the Elephant by the Danish government in 1947, he designed his own coat of arms which featured in the center a YinYang logo (Taiji symbol) with the Latin motto “contraria sunt complementa” or “opposites are complementary” (Figure 1).
While quantum mechanics recognized particle-wave complementarity, it stopped short of identifying the essence of YinYang bipolar coexistence. Without bipolarity any complementarity is less fundamental due to the missing “opposites” (see Figure 2). On the other hand, if bipolar equilibrium is the most fundamental form of

Figure 1. Bohr’s Coat of Arms (Creative Commons file by GJo, 3/8/2010, Source File: Royal Coat of Arms of Denmark. svg).
 (a) (b) (c) (d)
(a) (b) (c) (d)
Figure 2. Fundamental and non-fundamental complementtarities. (a) Fundamental; (b)-(d) Non-fundamental.
equilibrium, any multidimensional model in spacetime geometry cannot be most fundamental. In brief, actionreaction, particle-antiparticle, input-output, negativepositive energies, or the Yin and Yang of nature in general constitute the most fundamental opposites, but man and woman, space and time, particle and wave, truth and falsity are not exactly bipolar opposites. This could be the reason why Bohr believed that a causal description of a quantum process cannot be attained and quantum mechanics has to content itself with particle-wave complementary descriptions [2]. It may also be the reason why Bohr’s Copenhagen interpretation was challenged by the EPR thought experiment, Bohm’s wave function [7] was dismissed by Einstein as “too cheap” [8, p. 341], and Bell’s theorem stopped short of reaching logically definable quantum causality and had to rely on probability and statistical measures that is still been questioned.
Actually, following David Bohm [7], Bell relied on two entangled qubits in spin or polarization. In his theorem, spin-up (+) or spin-down (−) were used as essential concepts [4]. But Bell, like Bohr and Bohm, stopped short of developing an equilibrium-based dynamic logical system to account for the equilibrium and non-equilibrium states of negative-positive energies—the most fundamental Yin and Yang of nature.
While quantum computing has made progress, without quantum causality, the ubiquitous effects of quantum entanglement so far remains a mystery. For instance, the intrinsic relationships between quantum circuitry and biocellular networks are unknown. As a result, quantum cellular combinatorics remains an untouched gap between quantum computing, biological computing and human intelligence.
Is quantum causality logically definable? Further extending Bohr’s particle-wave complementarity principle and Bell’s theorem, this work introduces an equilibrium-based logical interpretation to quantum causality and entanglement for quantum logic gate design and quantum cellular combinatorics. First, bipolar dynamic logic (BDL) and bipolar quantum linear algebra (BQLA) are introduced. While BDL supports logically definable causality and generic quantum entanglement, BQLA provides algebraic causality and composite quantum entanglement. The two levels of causality and entanglements enable the generalization of quantum logic gate matrix from unipolar truth-based domain to bipolar equilibriumbased domain. This generalization presents a unification of digital computing, quantum computing and bio-cellular computing with a possible resolution to the EPR paradox. A scalable graph theory of quantum cellular combinatorics is introduced for ubiquitous quantum computing and quantum intelligence.
This paper is organized into six sections. Section 2 introduces BDL and BQLA. Section 3 discusses bipolar quantum (logic) gates and quantum causality with two levels of entanglement. Section 4 extends bipolar quantum gates to quantum cellular combinatorics. Section 5 presents an analysis and discussion. Section 6 draws a few conclusions.
2. Quantum Causality Is Logically Definable
2.1. Bipolar Dynamic Logic (BDL)
YinYang bipolar dynamic logic (BDL) presents an equilibrium-based extension to quantum computing [9-12]. BDL is based on bipolar sets whose elements are bipolar agents such as dipoles, particle-antiparticle pairs, nature’s action-reaction objects, genomic repression-activation capacities, social competition-cooperation relations, inputoutput of any system, self-negation and self-assertion abilities in mental health, in general, the negative and positive energies of nature (Figure 3). This ontological claim positioned BDL in the context of logically definable causality for ubiquitous quantum computing.
BDL is defined on 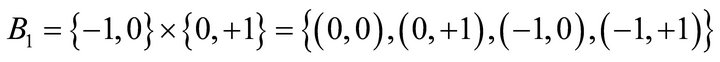 a bipolar quantum lattice in YinYang bipolar geometry as shown in Figure 4. The four values of B1 form a bipolar causal set which stand, respectively, for eternal equilibrium
a bipolar quantum lattice in YinYang bipolar geometry as shown in Figure 4. The four values of B1 form a bipolar causal set which stand, respectively, for eternal equilibrium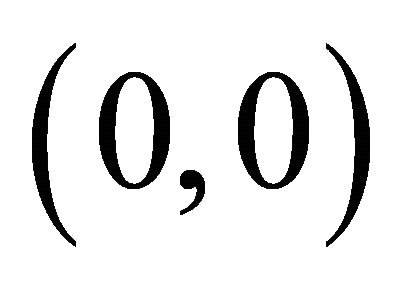 , non-equilibrium
, non-equilibrium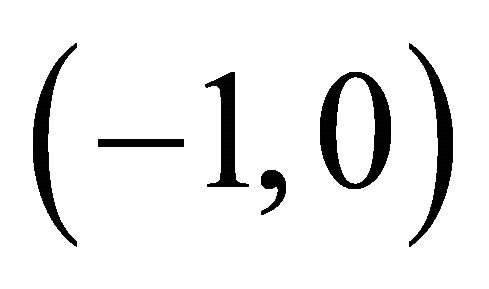 , non-equilibrium
, non-equilibrium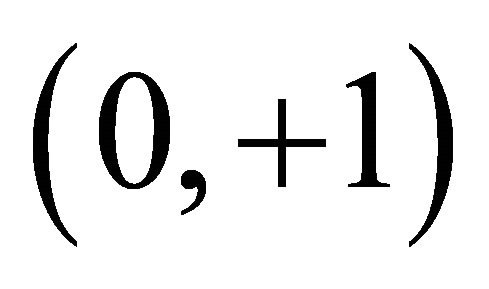 ; equilibrium
; equilibrium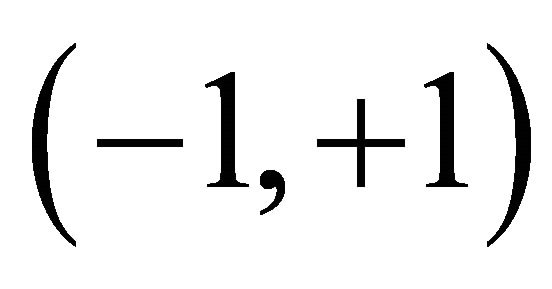 . Evidently, each bipolar element can be used to code two bits of binary information (or one bit with an OR or AND operation of the two poles in absolute values). Figure 5 illustrates bipolar interaction and entanglement.
. Evidently, each bipolar element can be used to code two bits of binary information (or one bit with an OR or AND operation of the two poles in absolute values). Figure 5 illustrates bipolar interaction and entanglement.
Equations (1)-(12) in Table 1 provide the basic operations of BDL. The laws in Table 2 hold on BDL. Bipolar universal modus ponens (BUMP) is listed in Table 3 which logically defines equilibrium-based bipolar causality. Truth tables of BDL are presented in Table 4. In BDL Å and Å- are “balancers”; Æ and Ä are intuitive “oscilla-

Figure 3. Multidimensional equilibrium or non-equilibrium deconstructed to bipolar equilibria/non-equilibria.
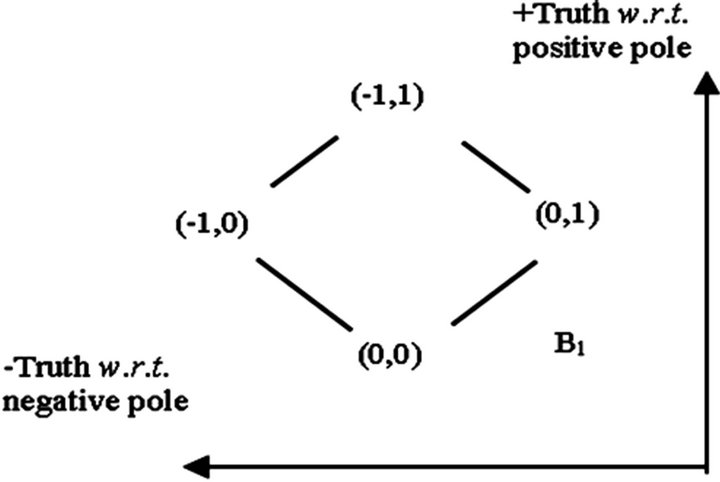
Figure 4. Hasse diagram of B1 in bipolar geometry.

Figure 5. Bipolar relativity: (a) Linear interaction; (b) Crosspole non-linear interaction; (d) Oscillation; (e) Bipolar entanglement.

Table 1. YinYang Bipolar Dynamic Logic (BDL).

Table 2. Laws of bipolar equilibrium/non-equilibrium.

Table 3. Bipolar Universal Modus Ponens (BUMP).
tors”; Æ− and Ä− are counter-intuitive “oscillators”; & and &- are “minimizers.” The linear, cross-pole, bipolar fusion, fission, oscillation, interaction and entanglement properties are depicted in Figure 5.
Thus, BDL presents a causal logic or a causal set approach to quantum computing. The causal set hypothesis is originally a quest for quantum gravity [13]. As a settheoretic model, however, causal sets did not go beyond classical truth-based set theory to reach logically definable quantum causality until bipolar sets and BDL.
2.2. Bipolar Quantum Linear Algebra (BQLA)
The bipolar lattice  can be naturally extended to the bipolar fuzzy lattice
can be naturally extended to the bipolar fuzzy lattice 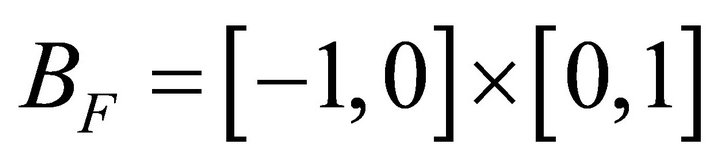 and real valued bipolar lattice
and real valued bipolar lattice . B1 and BF are bounded complemented unit square lattices, respectively; B¥ is unbounded.
. B1 and BF are bounded complemented unit square lattices, respectively; B¥ is unbounded. , Equations (13) and (14) define two algebraic operations.
, Equations (13) and (14) define two algebraic operations.
Tensor Bipolar Multiplication:
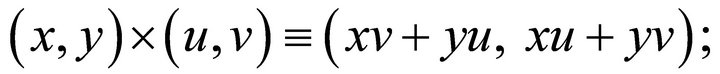 (13)
(13)
Bipolar Addition:
 (14)
(14)
In Equation (13), ´ is a cross-pole multiplication operator with the infused non-linear bipolar tensor semantics of , and
, and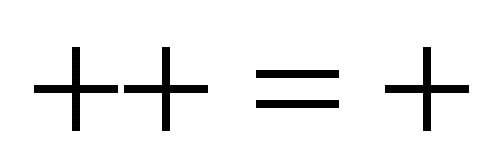 ; + in Equation (14) is a linear bipolar addition or fusion operator. With the logical and algebraic operations, classical linear algebra is naturally extended to an equilibrium-based bipolar quantum linear algebra (BQLA) with bipolar fusion, fission, diffusion, interaction, oscillation, annihilation, and quantum entanglement properties. These properties enable physical or biological agents to interact through bipolar quantum fields such as atom-atom, cell-cell, heart-heart, heart-brain, brain-brain, organ-organ, and genome-genome bioelectromagnetic quantum fields as well as biochemical pathways in energy equilibrium or non-equilibrium. Thus, the properties lead to the inception of bipolar atom and a new philosophy [14,15].
; + in Equation (14) is a linear bipolar addition or fusion operator. With the logical and algebraic operations, classical linear algebra is naturally extended to an equilibrium-based bipolar quantum linear algebra (BQLA) with bipolar fusion, fission, diffusion, interaction, oscillation, annihilation, and quantum entanglement properties. These properties enable physical or biological agents to interact through bipolar quantum fields such as atom-atom, cell-cell, heart-heart, heart-brain, brain-brain, organ-organ, and genome-genome bioelectromagnetic quantum fields as well as biochemical pathways in energy equilibrium or non-equilibrium. Thus, the properties lead to the inception of bipolar atom and a new philosophy [14,15].
Based on Equations (13) and (14), given input vector E and a bipolar matrix M we have Equation (15). While E is the input vector to a dynamic system characterized with the connectivity matrix M, V is the result column bipolar vector.
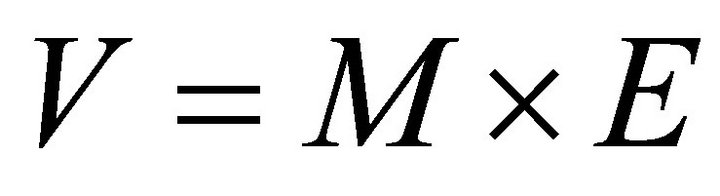 (15)
(15)
M can actually be a bipolar generalization of a quantum gate matrix. The generalization is made possible by BDL and BQLA. With the generalization we have the following definition of energy and equilibrium.
The energy of a bipolar element or bipolar matrix is the absolute total of the negative and positive sides.
For instance, the absolute energy of a bipolar element 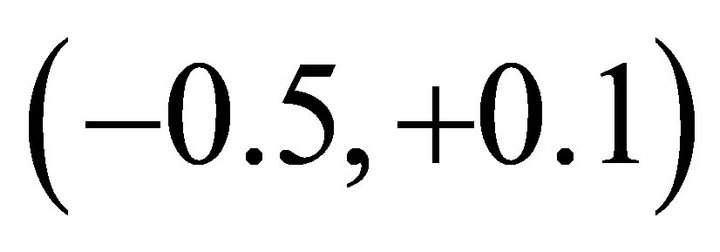 can be defined as
can be defined as

Bipolar Energy Conservational Quantum Gate. If the energy of every row and every column of a bipolar decimal matrix M in Eq. (15) always adds up to 1.0, we call M a bipolar energy conservational quantum gate matrix.
Law of Bipolar Equilibrium or Symmetry: " V, M, E, if M is a unitary quantum gate matrix, 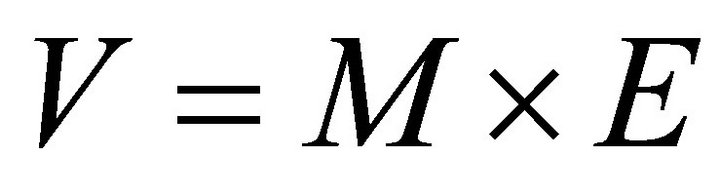 satisfies Equation (16).
satisfies Equation (16).
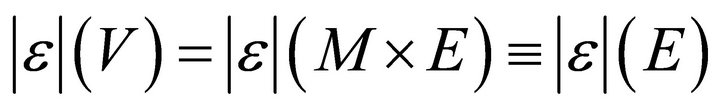 (16)
(16)
Evidently, any integer unitary quantum gate matrix must be energy conservational. Therefore, a unitary quantum gate can be deemed part of energy conservation or equilibrium for reversibility.
3. Bipolar Quantum Gates and Quantum Entanglement
3.1. Logical Examples
Similar to classical linear matrix, the matrix M in Equation (15) as a causal set can be used to characterize a bipolar quantum gate. Using BDL and BQLA we design two such gates to illustrate the basic ideas in the following.
Gate 1. B-NOT Gate (Bipolar NOT Gate):
Graph form:

Bipolar Matrix M1 (Satisfies Equation (16)):

In simplified unipolar forms
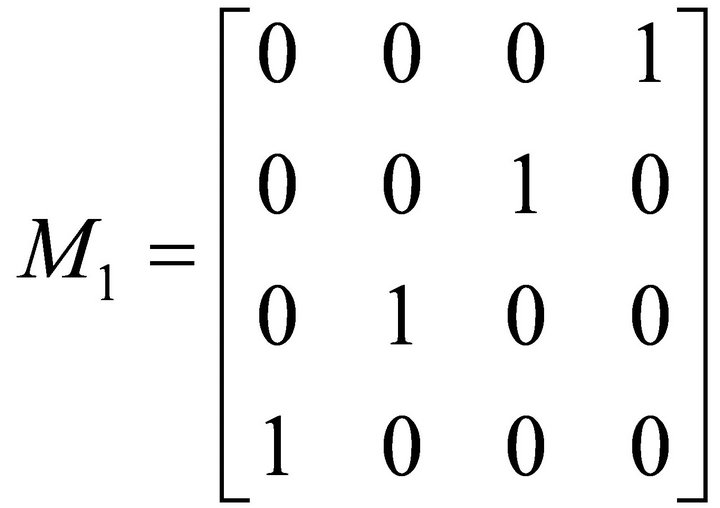
Interestingly, if we regard the ordered bipolar causal set 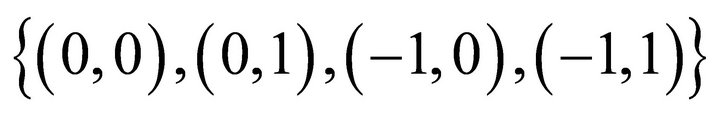 as equivalent to the set of basis states
as equivalent to the set of basis states 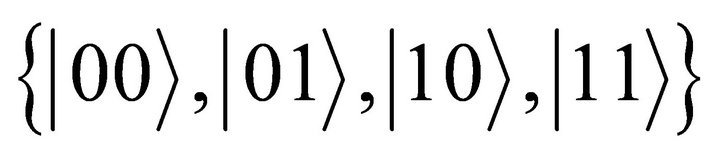 we have
we have
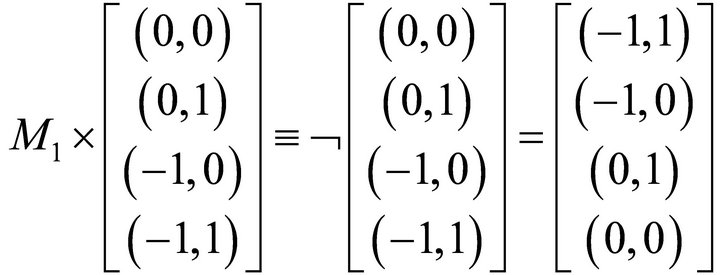
which would be equivalent to
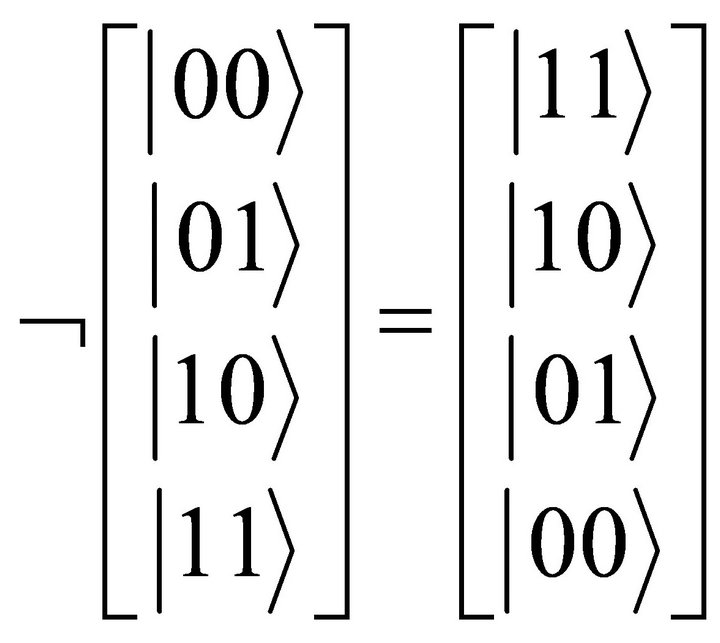
Noticeably, the matrix M1 is similar to controlled NOT gate (C-NOT or XOR gate) but fundamentally different. Using bipolar quantum linear algebra, we can apply the quantum gate matrix directly to an input bipolar column vector and do not have to go through the eigenvalues of each basis state.
Different from unipolar quantum computing, bipolar quantum logic provides bipolar negation operation in addition to the B-NOT operator.
Gate 2. B-NEG Gate (Bipolar Negation Gate):
Graph form:

Bipolar Matrix M2 (Satisfies Equation (16)):

or in simplified form

Evidently, we have
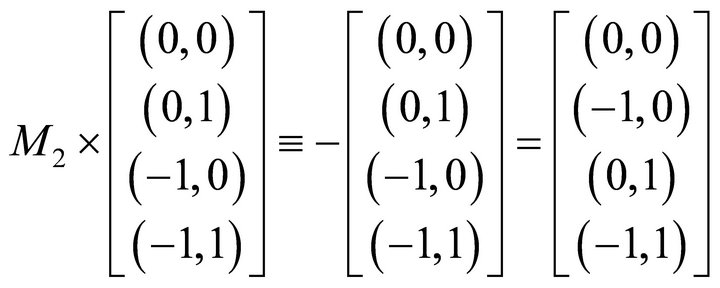
Certain B-NOT and B-NEG equivalence could be technically interesting in quantum gate design such as

Similarly, we can define other bipolar gates such as B-Ä and B-Å gates. It can be shown that Toffoli gate can be extended to bipolar Toffoli gate for simulating bipolar NAND gate. This will be reported in another paper.
3.2. Quantum Mechanical Implementations
Physical implementation of BDL or BQLA can be in different ways such as using quantum dots, atoms, trapped ions or superconductors. A bipolar qubit register [12, Ch.7] is shown in Figure 6(a), which consists of two Bloch spheres, one holds a negative quantum dot and another holds a positive one. When both dots are inside the rectangle box it may register a 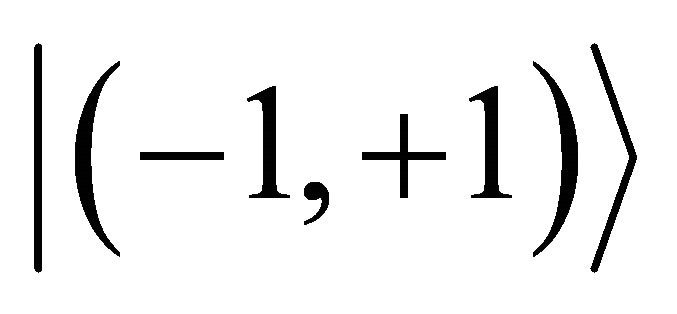 state; if both are outside the box, it may register a
state; if both are outside the box, it may register a  bipolar state; if the negative dot is inside but the positive one is outside, it may register a
bipolar state; if the negative dot is inside but the positive one is outside, it may register a  state; otherwise, it may register a
state; otherwise, it may register a  state. When probability coefficients are taken into consideration, the box creates a macroscopically coherent bipolar superposition, of the form
state. When probability coefficients are taken into consideration, the box creates a macroscopically coherent bipolar superposition, of the form 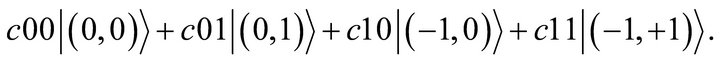 The bipolar quantum register seems to present a white-box resolution to Schrödinger’s cat paradox.
The bipolar quantum register seems to present a white-box resolution to Schrödinger’s cat paradox.
The bipolar superposition is fundamentally different from that of a traditional 2-qubit system in the form of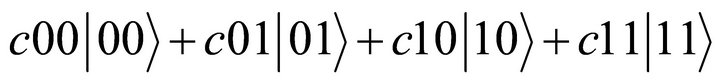 . While the traditional basis states are binary bit patterns without quantum causality and basis state entanglement, the bipolar basis states are logical values in BDL that form a bipolarcausal sets and lead to basis state quantum entanglement formally defined in the form of BUMP. (Note: Without losing generality we limit the scope of this work on basis state quantum causality and entanglement).
. While the traditional basis states are binary bit patterns without quantum causality and basis state entanglement, the bipolar basis states are logical values in BDL that form a bipolarcausal sets and lead to basis state quantum entanglement formally defined in the form of BUMP. (Note: Without losing generality we limit the scope of this work on basis state quantum causality and entanglement).
 (a)
(a) (b)
(b)
Figure 6. (a) Bipolar Qubit; (b) Bipolar Bloch sphere of a 2-electron system.
Alternatively, a 2-electron model (Figure 6(b)) can be used to illustrate equilibrium or symmetry with modularity. The entanglement of two electron systems has been reported in the literature [16]. But, to the author’s knowledge, besides BDL no other causal logic is reported for such a system. An immediate question is measurability.
Three reasonable assumptions can be made:
(1)  is stronger than
is stronger than  in spin energy;
in spin energy;
(2) 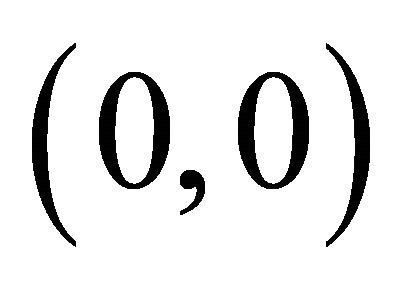 remains symmetrical to
remains symmetrical to ;
;
(3) 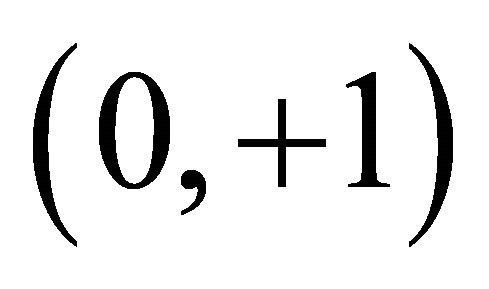 remains symmetrical to
remains symmetrical to .
.
It is clear that B-NOT gate can flip the quantum states in Figure 6(b) to their symmetrical ones in Figure 7(a). Such a flip is reversible both physically and logically. Logically, we have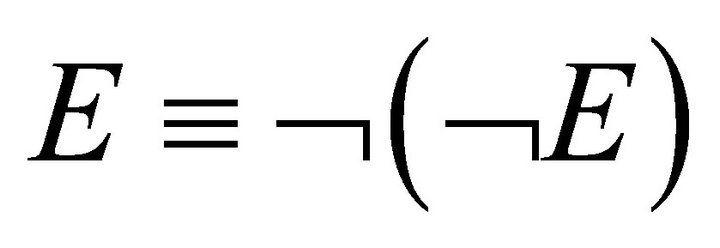 . Similarly, B-NEG gate is also reversible with
. Similarly, B-NEG gate is also reversible with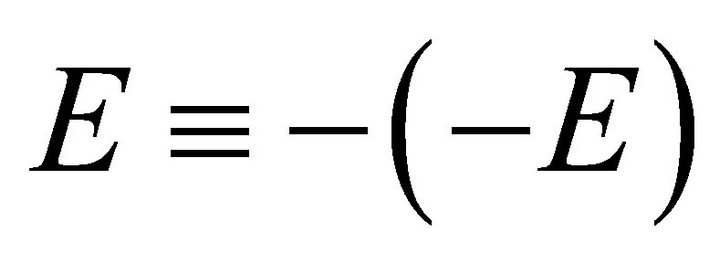 as shown in Figure 7(b).
as shown in Figure 7(b).
3.3. Generic Bipolar Quantum Entanglement
Mainstream quantum computing inherits some binary features from classical digital computing. This heritage has never been challenged. Despite repeated verification of faster than light observations [17], quantum causality and entanglement finds no logical interpretation. Bipolar quantum causality and entanglement present a major deviation from the binary heritage and it may hold the key for scalable modular quantum logic gate design.
It is interesting to note that two entangled single electron systems, no matter how far away they are separated,
should satisfy bipolar quantum causality as defined by BUMP (Table 3). BUMP in the form
 simply states: If bipolar logical variables f andj are bipolar equivalent (or entangled) in the background independent YinYang bipolar geometry (Figure 4), any bipolar interaction
simply states: If bipolar logical variables f andj are bipolar equivalent (or entangled) in the background independent YinYang bipolar geometry (Figure 4), any bipolar interaction  implies the bipolar interaction
implies the bipolar interaction  or vice versa. Thus, BUMP defines a bipolar causal relation that provides the first equilibrium-based logical interpretation for the mysterious quantum correlation.
or vice versa. Thus, BUMP defines a bipolar causal relation that provides the first equilibrium-based logical interpretation for the mysterious quantum correlation.
It is posited [12,14,15] that:
Postulate 1. Bipolar quantum entanglement is the most fundamental entanglement.
Postulate 2. YinYang bipolarity is the most fundamental property of the universe.
The two postulates are actually logically provable axioms. For postulate 1 if a bipolar value characterizes the energy superposition of gravitational and quantum action-reaction, an atom would be a set of bipolar elements (Figure 6). As the total must be equal to the sum, without bipolar quantum entanglement there would be no atom level quantum entanglement. Postulate 2 follows postulate 1.
Another proof comes from established observations in quantum mechanics. It is well-known that pairs of particles can be generated so that they are in some specific quantum states. For instance, a pair of these particles may be generated having a two-state spin: when one spin is up the other must be down. This type of entangled pair with opposite spin, is known as the spin anti-correlated case. This kind of entanglement is central in quantum teleportation and cryptography but so far it has not been described in logical form. With BUMP in BDL, the entanglement can be characterized as

Generalization of Bipolar Quantum Entanglement. To further extend BDL for quantum causality, we use W as a generalized symbol to include spin anti-correlated entanglement in addition to Û. With this generalization, all observed generic cases can be characterized as, 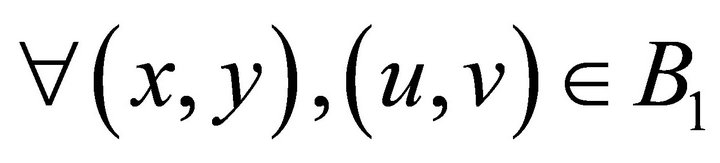 , either
, either

Thus, BUMP has led to generic level quantum entanglement in a background independent bipolar geometry. A bipolar qubit register (Figure 6(a)) can characterize a bipolar variable in BUMP for generic bipolar quantum entanglement. Evidently, B-Neg and B-Not gates may play an important role in quantum entanglement.
3.4. Composite Quantum Entanglement
Generic entanglement is logically strict. However, in the generic case variables in BUMP has to be fundamental subatomic particles, antiparticles, or a pair of them that doesn’t account for atom level entanglement with many such pairs of subatomic particles.
While Figure 6(b) is a simple illustration to the two postulates, Figure 8 gives a more obvious illustration where both matter and antimatter atoms can be characterized as a composite set of bipolar elements and unified with Equation (15) [14].
From a computational perspective, bipolar causality can be characterized by measuring one entangled atom and then to predict the other far away like in quantum teleportation. For instance, if two entangled and then separated atoms have the states
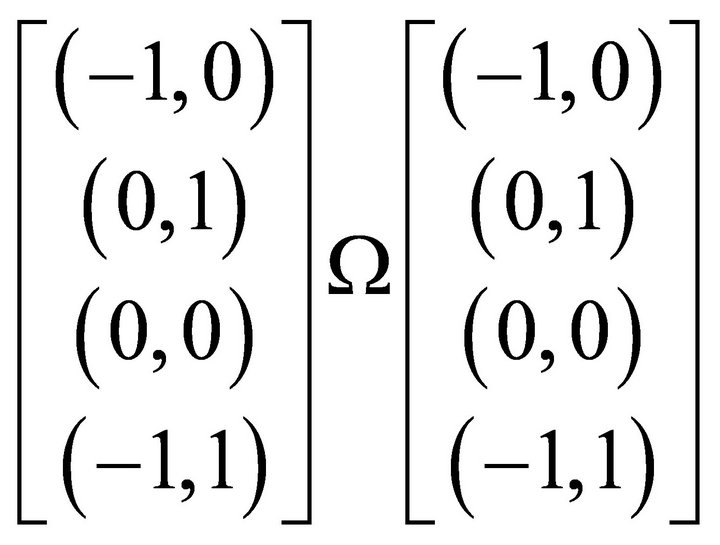
By applying the B-NEG operation to the first atom, the state of the 2nd one can be predicted using the following equivalence within the background independent bipolar geometry:

The above example is intuitive as both sides are in the same order. Interestingly, we may have the following entanglement:

This is a rather counterintuitive but a possible spin anti-correlated case. The counterintuitive nature is due to the background independent property of YinYang bipolar geometry. However, the entanglement (if possible) does not violate any equilibrium, symmetry and reversibility principles. In quantum lattice form it is equivalent to 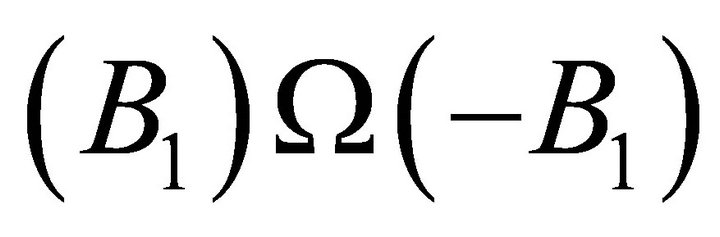 (see Figure 9).
(see Figure 9).
Similarly, we may have the following complementary entanglement:
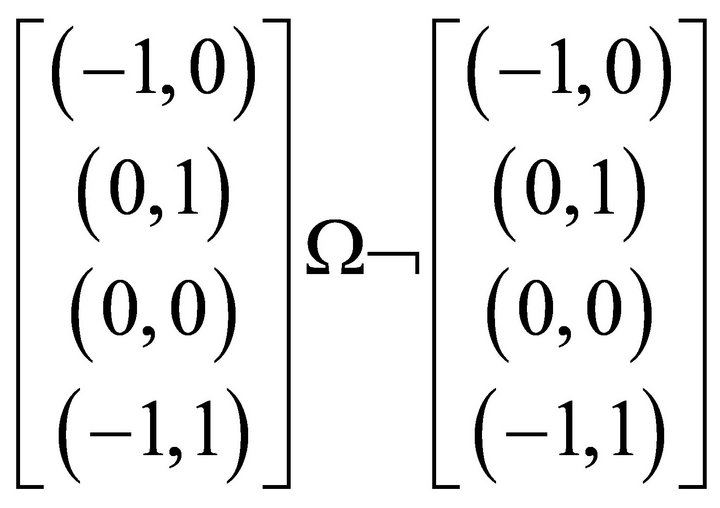
which can be equivalently described in quantum lattice form 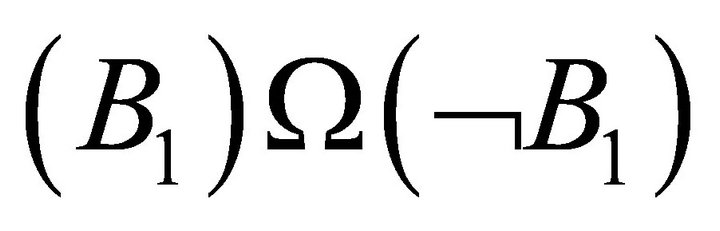 in Figure 10. From Figure 10, it is clear that the composite entanglement (if possible) does not violate any equilibrium, symmetry and reversibility principles.
in Figure 10. From Figure 10, it is clear that the composite entanglement (if possible) does not violate any equilibrium, symmetry and reversibility principles.
Furthermore, assuming reversible quantum entanglement or teleportation we would have faster than light information transmission such as 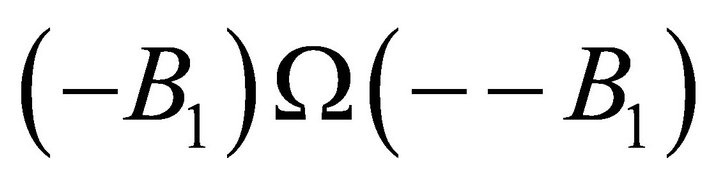 and
and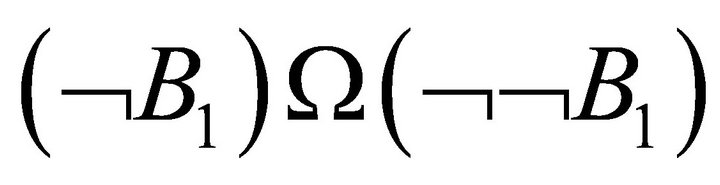 :
:
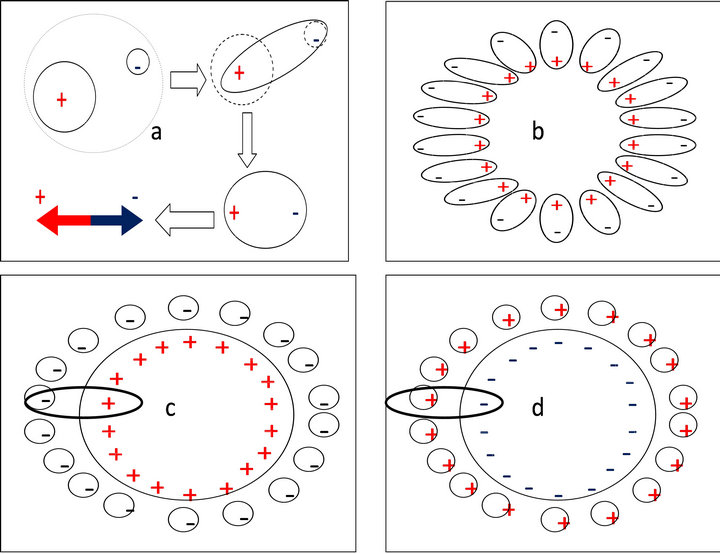
Figure 8. (a) Bipolar representation of hydrogen atom; (b) YinYang n-elements; (c) Matter atom; (d) Antimatter atom.

3.5. Reversibility
Bipolar quantum entanglement should be classified as background independent basis state entanglement in YinYang bipolar geometry where quadrant is irrelevant (Figure 4). This property makes logical reversibility [18,19] possible for BDL.
Theorem 1 (Reversibility Theorem): Bipolar quantum logic gate design can achieve logical reversibility–a step toward bipolar universal quantum computing.
Proof. It follows from (A) BDL subsumes Boolean logic [12, Ch.3]; (B) B-NOT and B-NEG gates are both reversible; and (C) the following logical equivalence observations hold (see proof in [12, Ch.3]:
B-AND (&) gate is bipolar linearly equivalent to Boolean AND gate.
B-OR (Å) gate is bipolar linearly equivalent to Boolean OR gate.
B-TENSOR (Ä) gate can be decomposed to the following cases:
(1)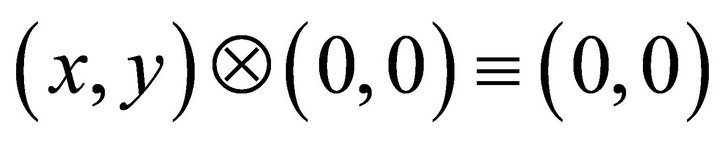 , equivalent to NULL gate;
, equivalent to NULL gate;
(2) , equivalent to IDENTITY gate;
, equivalent to IDENTITY gate;
(3) , equivalent to B-NEG gate;
, equivalent to B-NEG gate;
(4)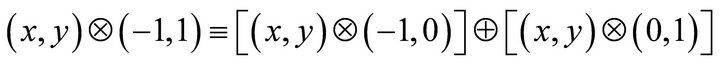 , that is equivalent to the B-OR of a B-NEG operation.
, that is equivalent to the B-OR of a B-NEG operation.
From the four cases we see that case (1) is the NULL law; case (2) is the identity law; case (4) is a composition of case (2) and (3); the essential case is number (3)—the B-NEG gate. Since the other gates &−, Å−, and Ä− are the B-NEG of &,Å and Ä, respectively, and since existing (unipolar or 2-dimensional) quantum logic gates have achieved reversibility, it is clear that bipolar logical reversibility is achievable based on BDL. ÿ
4. Quantum Cellular Combinatorics
4.1. An Equilibrium/Non-Equilibrium Approach
Combinatorics is a branch of mathematics concerning the study of finite or countable discrete structures. Aspects of combinatorics include counting the structures of a given kind and size, deciding when certain criteria can be met, and constructing and analyzing objects meeting the criteria, finding “largest”, “smallest”, or “optimal” objects, and studying combinatorial structures arising in an algebraic context, or applying algebraic techniques to combinatorial problems (algebraic combinatorics).
Combinatorial problems arise in mathematics with many applications. One of the oldest and most accessible parts of combinatorics is graph theory, which also has numerous natural connections to other areas. Combinatorics is used frequently in computer science to obtain formulas and estimates in the analysis of algorithms.
BDL and BQLA provide a unique logical and mathematical basis for bipolar quantum combinatorics. The new approach is equilibrium-based on the negative or positive energies [20] or the Yin and Yang of nature [14,15,21-29]. This focus is expected to foster ubiquitous quantum computing and quantum intelligence in both social and natural science.
4.2. Combinatorial YinYang-1-Element Graph
Figure 11 shows the graph of a YinYang-1-element as the most basic structure of QCC. This element seems to be rather simple. But a closer examination reveals its quintessential role as the smallest and, at the same time, the largest structure in the new type of combinatorics for quantum cellular computing.
First, we consider it as a smallest agent with equilibrium or non-equilibrium. In this case, it can be used as a model for a particle-antiparticle pair variable
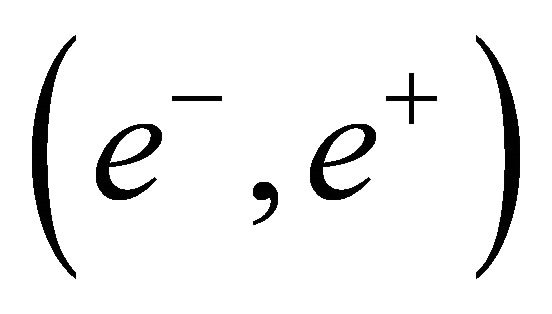 or an energy input-output variable. For instance, if
or an energy input-output variable. For instance, if  it can represent an electron or non-equilibrium; if
it can represent an electron or non-equilibrium; if 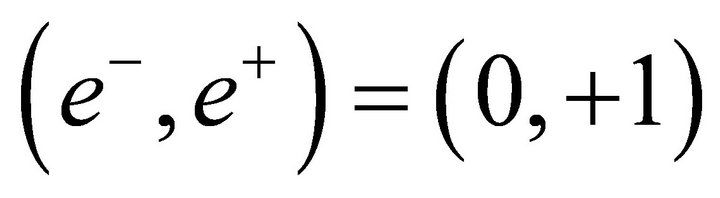 it can represent a positron or another non-equilibrium; if
it can represent a positron or another non-equilibrium; if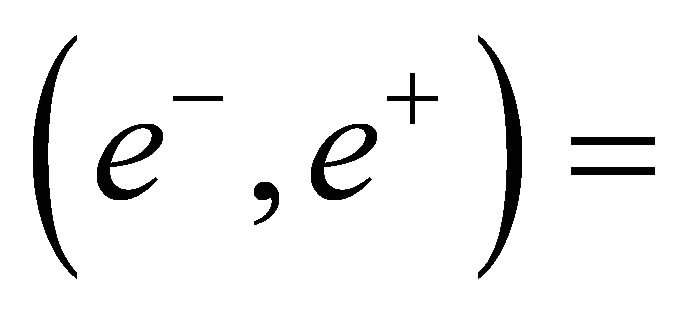
 it can represent an electron-positron pair or an energy equilibrium; if
it can represent an electron-positron pair or an energy equilibrium; if 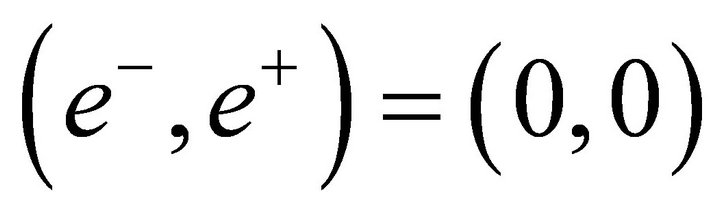 it can represent an annihilation of the pair or eternal equilibrium.
it can represent an annihilation of the pair or eternal equilibrium.
Interestingly, the reflexive link can also be bipolar to add dynamic change or mutation to the agent. Different from unipolar reflexivity, in the bipolar case we may have positive reflexivity , negative reflexivity
, negative reflexivity , or bipolar reflexivity
, or bipolar reflexivity  characterized with three different colors, respectively. For instance, if the reflexive link weight is
characterized with three different colors, respectively. For instance, if the reflexive link weight is , when n is odd we have
, when n is odd we have and when n is even we have
and when n is even we have . This property seems rather bizarre but it can represent the most fundamental natural or biological oscillation processes in microscopic as well as macroscopic worlds. For instances, a subatomic particle can change polarity three trillion times per second between matter to antimatter [30]; some genetic agent exhibits YinYang bipolar repression-activition
. This property seems rather bizarre but it can represent the most fundamental natural or biological oscillation processes in microscopic as well as macroscopic worlds. For instances, a subatomic particle can change polarity three trillion times per second between matter to antimatter [30]; some genetic agent exhibits YinYang bipolar repression-activition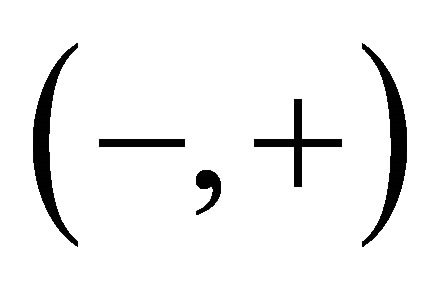 abilities in gene expression regulation [22].
abilities in gene expression regulation [22].
Secondly, we consider YinYang-1-element as the largest equilibrium or non-equilibrium. Evidently, our universe can switch from big bang 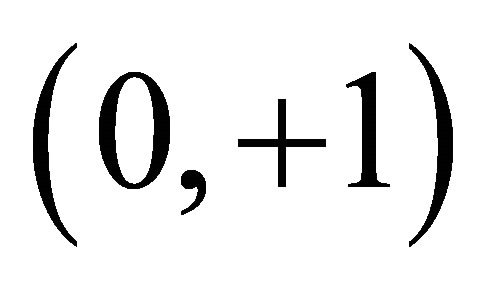 state to a black hole state
state to a black hole state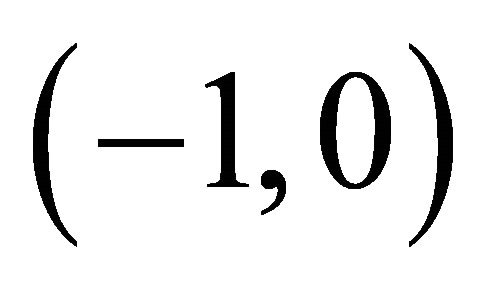 . This can be characterized as
. This can be characterized as  . Interestingly, it may also switch from a black hole state to a big bang state which can be characterized as
. Interestingly, it may also switch from a black hole state to a big bang state which can be characterized as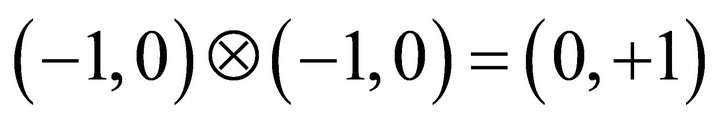 . In this case, we have a cyclic process model
. In this case, we have a cyclic process model 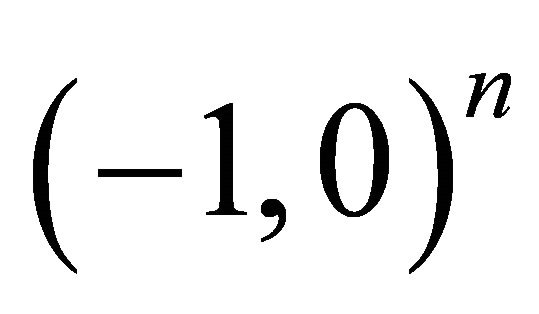 for our universe.
for our universe.
If we assume a negative reflexive link and an adaptive bipolar element, we could have
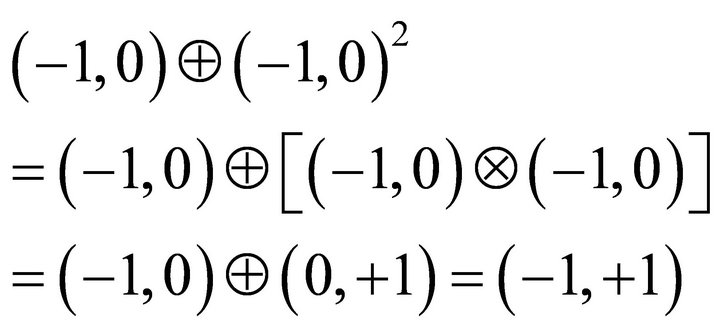
which shows a self-adaptation of  to bipolar equilibrium
to bipolar equilibrium  for an agent, small or large [12]. The key is self adaptivity characterized by Å and Ä in combination with memory ability.
for an agent, small or large [12]. The key is self adaptivity characterized by Å and Ä in combination with memory ability.
Of course, if reflexivity is defined as ´ instead of Ä and the reflexive link weight is bipolar balanced,  and
and , following Equation (13), we have
, following Equation (13), we have  and, in addition, we must have
and, in addition, we must have
 (17)
(17)
Remarkably, Equation (17) defines the law of global energy equilibrium regardless of local bipolar balance or imbalance. This exhibits the significance of the bipolar generalization. Without bipolarity, causality, quantum entanglement and energy equilibrium would be impossible.
Thirdly, we consider YinYang-1-element as a medium-sized equilibrium or non-equilibrium. This may sound impossible. But, evidently, a person’s mind can be in depression , mania
, mania , equilibrium (−1, +1), eternal equilibrium
, equilibrium (−1, +1), eternal equilibrium  or between (−0.6, +0.7). Actually, all human beings have to be in either mental equilibrium or non-equilibrium or between. To certain extent, we are all mentally bipolar, either in equilibrium or disorder or between because no one’s mind can escape equilibrium or non-equilibrium and bipolar equilibrium/ non-equilibrium is most fundamental. In this case
or between (−0.6, +0.7). Actually, all human beings have to be in either mental equilibrium or non-equilibrium or between. To certain extent, we are all mentally bipolar, either in equilibrium or disorder or between because no one’s mind can escape equilibrium or non-equilibrium and bipolar equilibrium/ non-equilibrium is most fundamental. In this case  can characterize the mental adaptation from depression to equilibrium [31,32].
can characterize the mental adaptation from depression to equilibrium [31,32].
4.3. Combinatorial YinYang-2-Element Graph
Figure 12 shows the structures of a YinYang-2-element graph as the 2nd most basic structure of QCC for bipolar interaction. These structures added two more bipolar links between the two bipolar elements in equilibrium or non-equilibrium (green: harmonic; red: positive; blue: negative).
A link weight can be any  in B¥ . For instance,
in B¥ . For instance, 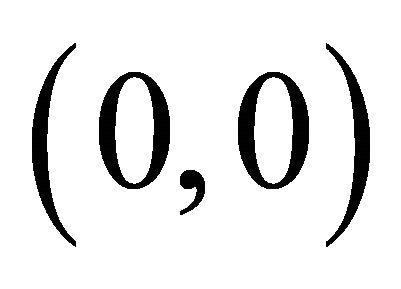 shows no interaction;
shows no interaction;  shows conflict or inhibition to each other;
shows conflict or inhibition to each other;  shows coalition or excitation to each other;
shows coalition or excitation to each other; 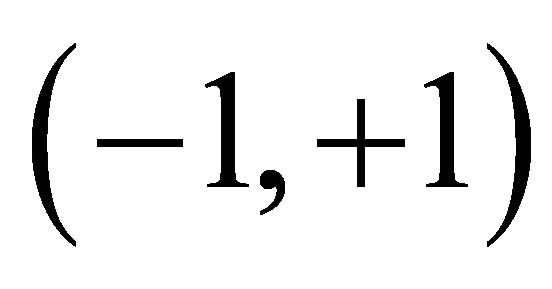 shows harmonic interaction. As a basic combinatorial graph for equilibrium or non-equilibrium bipolar interaction, YinYang-2-element is critical in characterizing bipolar quantum entanglement for building larger combinatorial networks.
shows harmonic interaction. As a basic combinatorial graph for equilibrium or non-equilibrium bipolar interaction, YinYang-2-element is critical in characterizing bipolar quantum entanglement for building larger combinatorial networks.
4.4. Combinatorial YinYang-N-Element Graph
Figure 13 shows YinYang-3- and YinYang-4-element graphs. Figure 14 shows a YinYang-5-element graph. Figure 15 shows a YinYang-n-element graph. The 3-