The Conservation Laws and Stability of Fluid Waves of Permanent Form ()
1. Introduction
This paper is based on Nekrasov’s integral equation solution obtained in [1,2]. This solution allows us to find the profile and velocity of a gravitational wave, and the calculation of the wave kinetic and potential energy is possible. At fixed depth of fluid the solution of Nekrasov’s integral equation exists on a limited segment of wavelength 
The potential and full mechanical energies are monotonically increasing functions on the segment
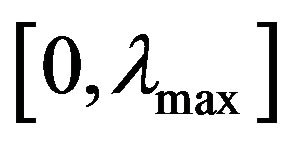. From the law of the change of wave’s kinetic energy presented in [3] as mathematical theorem follows that the kinetic energy vanishes on the boundaries of the segment 
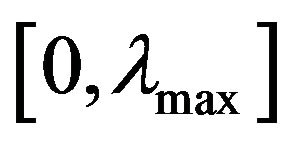and has the maximum at a point 
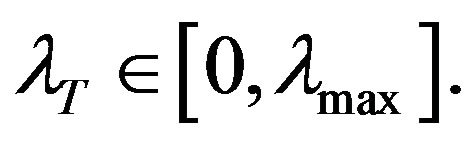Thus we observe symmetry: at the points 
the full mechanical energy consists only of potential energy. The wave of constant shape may be considered as a compound pendulum with a suspension center in the origin of coordinates arranged on unperturbed surface of fluid.Then the wave stability is spotted as a compound pendulum stability.
The plan of the paper is as follows. In Section 2, we describe the method of Nekrasov’s integral equation solution. Here this method has been used for evaluation of the maximum wavelength 
boundaries and for estimation of the maximum slope of the wave free surface.
In Section 3, geometrical and energy properties of a wave are explored and the theorem about the change of the wave velocity on the segment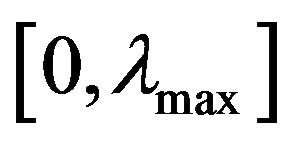 
is proved. As a result we have gained the laws of the change of wave’s kinetic and potential energy. Here we have defined the wave’s center of mass as a function of depth-towavelength ratio and have made some suppositions concerning the wave stability considering it as a compound pendulum.
2. Solution of Nekrasov’s Integral Equation
Nekrasov’s integral equation describing steady state waves of unchangeable shape on the surface of a fluid with finite depth 
is written as [4]
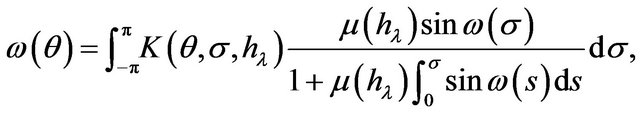(1.1)
where 
- is the polar angle, 
- is the angle that the wave surface makes with the horizontal, 
- is the wavelength, 
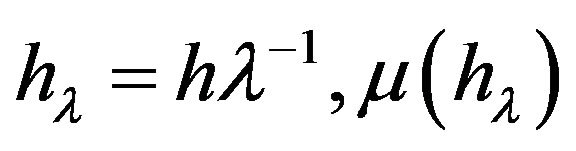- is an arbitrary constant,
From Equation (1.1) follows that required function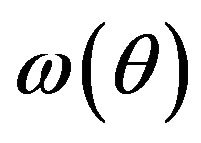 
represents a trigonometric series
(1.2)
The evaluation of scalar product
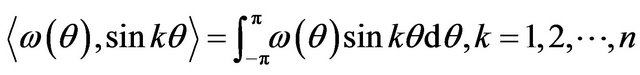
taking account of Equations (1.1) and (1.2) gives a system of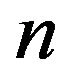 
nonlinear integral equations
(1.3)
where the subscript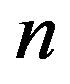 
denotes that in Equation (1.1) a truncated kernel 
with 
instead of 
is used. Below the subscript 
of any function will be omitted if
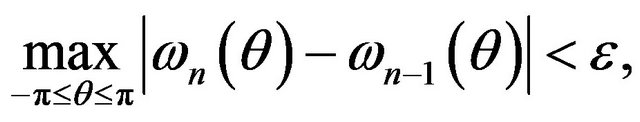(1.4)
where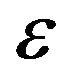 
- is a suitable from accuracy point of view small number The system (1.3) containing 
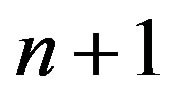unknowns 
is underdetermined and has a set of solutions including the trivial.
We assume that the first coefficient 
is independent of 
and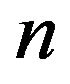 
and can be calculated from the linearized on 
system (1.3) at 
Thus
satisfy the equation
(1.5)
This equation has been solved by Kellogg’s method [5] in [1,2]. Let us remark that the Kellogg method was applied to a non-linear integral equation and the discovered solution is not spectral. In accordance with [2], Equation (1.5) has a unique solution (the motionless point) 
Now we fix in (1.3)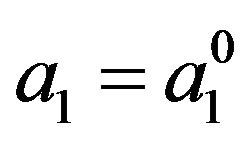 
and consider 
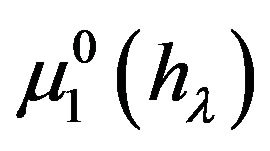as the initial approximation of 
After that, the system of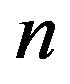 
Equations (1.3) contains n unknowns 
and has a solution that cannot be trivial.It has been shown [1,2] that coefficient 
satisfy system (1.3) at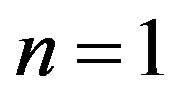 
if
where
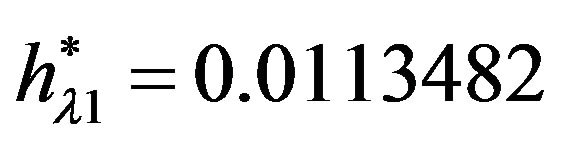(in [2] 
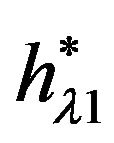is designated as
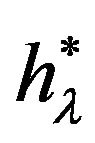).This means that the solution of the system (1.3) at 
exists and is unique if the wavelength 
where 
The lower boundary of the segment 
on which coefficient 
satisfy system (1.3) at 
can be obtained by solving the system
(1.6)
derived from (1.3) by substitution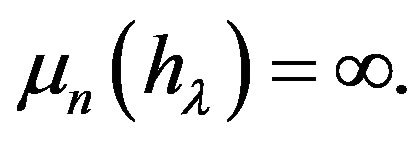 
If requirements (1.4) are satisfied, then the function 
is defined on the segment 
(see [1]), or on the equivalent segment
(1.7)
The system (1.6) containing n unknowns
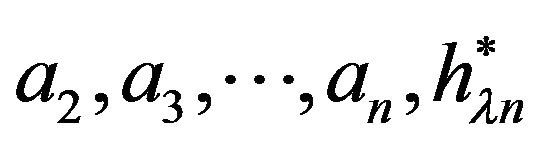was solved by successive approximations method at 
limited by computer’s throughput. The results of calculations of 
are given below:
The function 
is of low accuracy at the point 
and allows only to write the inequalities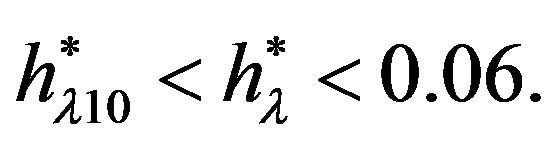 
From these inequalities follows that the maximal wavelength 
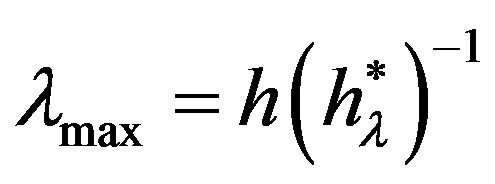is bounded on both sides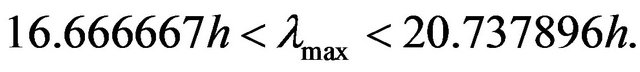 
The results of calculations of 
for 
are given below:
These numerical results assert that 
will remain the solution of system (1.3) at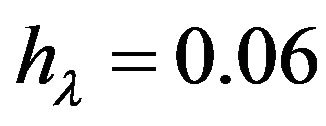 
for any 
From the solution of the system (1.6) we obtain the coefficients of the function
. This function achieves the maximum 
at the points
The maximum slope of the free surface in degrees 
exceeds the value 
received in [6]. We suppose that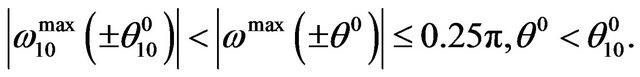 
3. The Conservation Law of Full Mechanical Energy and Stability of a Wave
For evaluation of a wave square and full mechanical energy we need the parametric equations of wave’s surface coordinates
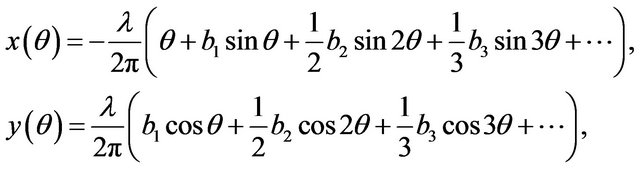
(2.1)
and the function
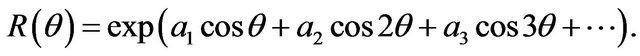(2.2)
Coefficients 
are determined as algebraic expressions of 
[2].
The coordinate origin O is on vertical line through the wave crest at distance h from the bottom,the 
axis is directed upward, and the 
axis to the right. In a coordinate system attached to the wave the bottom moves from right to left at velocity [4]
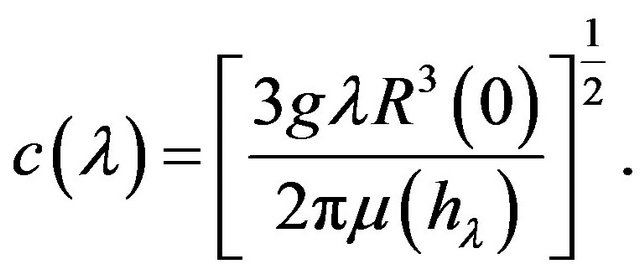(2.3)
Using (2.1)-(2.3) at fixed
, we obtain the expressions for the properties of the wave: the surface area
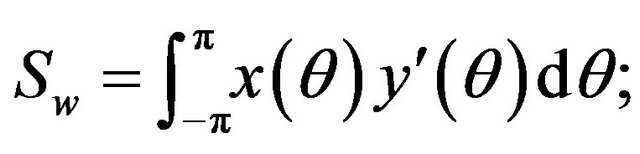(2.4)
the coordinates of the center of mass
(2.5)
the kinetic energy
(2.6)
where constant 
denotes the fluid density; the potential energy
(2.7)
the full mechanical energy
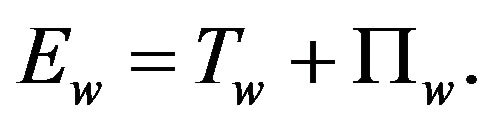(2.8)
The full mechanical energy of an unperturbed fluid layer with depth h and wavelengths 
is considered as
(2.9)
Substituting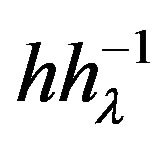 
for 
in (2.4)-(2.9), we get
and 
where
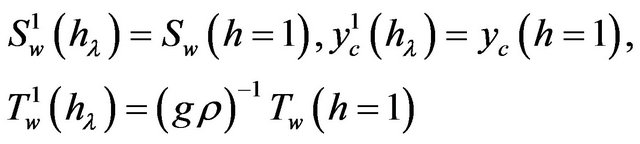
are integrals depending on parameter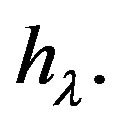 
Using these relationships we can write the Equations (2.6)-(2.8) in the form
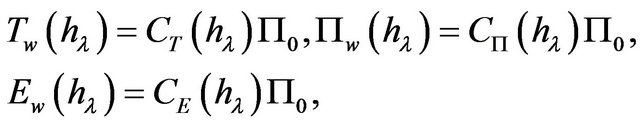(2.10)
where
The solution of system (1.3) obtained in [2] allow us to calculate the function 
on the segment 
On the boundaries of this segment we have
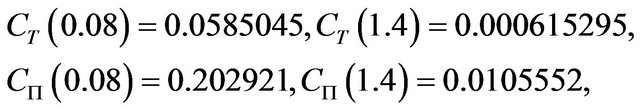
The functions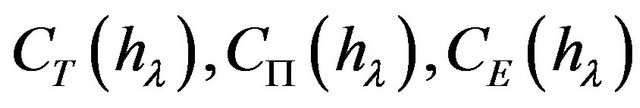 
calculated on the segment 
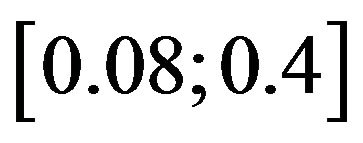are shown on Figure 1. The outcomes of these calculations allow to assert that the wave potential energy 
as function of parameter
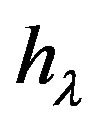monotonically diminishes on the segment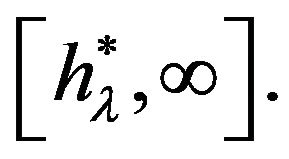 
In order to calculate the greatest value of potential energy of a wave we need the 
solution of system (1.6) instead of 
(see above).
The law of the wave kinetic energy change is formulated in the form of a mathematical theorem in [3]. This theorem asserts that: 1) for any constant depth of fluid 
the wavelength 
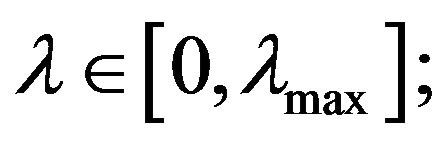2) at the boundaries of the segment 
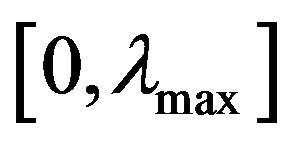the wave velocity
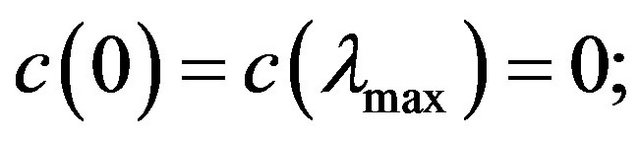3) there is a value 
at which
and the wave velocity is maximum, i.e. 
Let’s prove the points 1) - 3). 1) From (1.7) follows that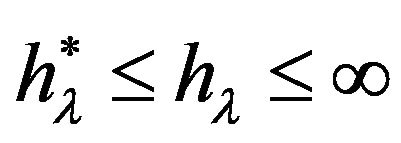 
and therefore 
2) Suppose the solution 
of (1.6) is known and satisfy (1.4). Using this solution we write the integrals
(2.11)
The first integral is known 
the integral 
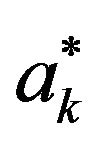tends to zero as 
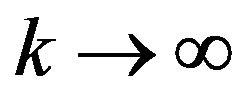(see [7]). Now it is possible to express the coefficients 
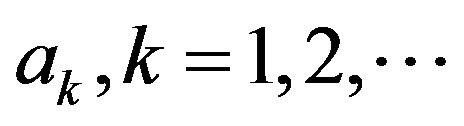from the system (1.6) in terms of the integrals 
We have
(2.12)
Taking into account 
as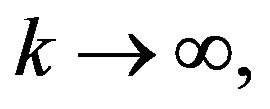 
from (2.12) follows that series 
is converging independently of convergence or divergence of the series 
Now if we recall (1.7), (2.3), and (2.12), we get 
Figure 1. The functions CT(hλ), CII(hλ), CE(hλ) for 0.08 ≤ hλ ≤ 0.4.
Let as remark that the convergence of series 
has been proved at a limited 
in [4] and for a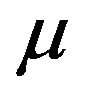 
presented as a converging series in [8].
3) Since the function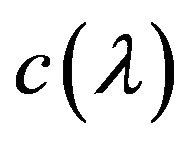 
vanishes at the boundaries of the interval 
it follows from the Rolles theorem [7] that exists at least a point
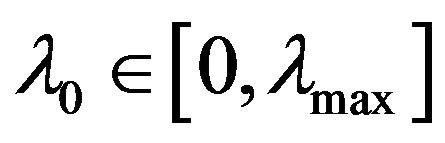such that 
As the numerator and denominator of right side of Equation (2.3) are strictly increasing functions of 
the point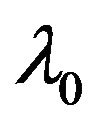 
is single and 
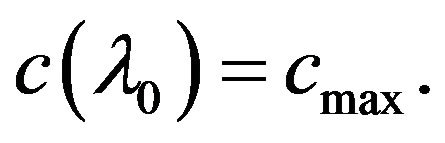The values
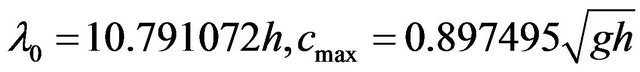have been calculated in [2].
The kinetic energy of the wave vanishes at boundaries of the segment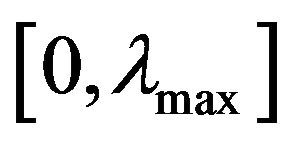 
and reaches the maximum at a point 
(This point is not presented on Figure 1). The full mechanical energy of a wave is a monotonically decreasing function on the segment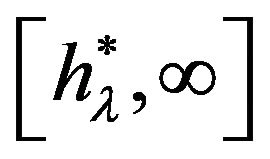
, but vanishes only at the point 
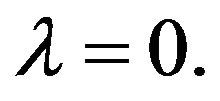We note also that the profiles of the waves calculated on the segment 
obey the law of mass conservation 
The stability of Nekrasov’s waves has been considered in [9]. We proceed from the fact that a liquid maintaining the invariable shape without a vessel, does not suspect that is a fluid.We suppose that a steady state wave can be presented as a compound pendulum with a suspension center in the origin of coordinates. This wave is stable if
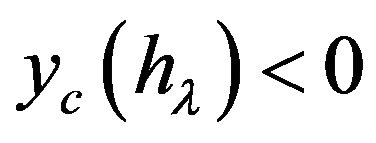and unstable if 
The function
is presented on Figure 2. This function has the greatest value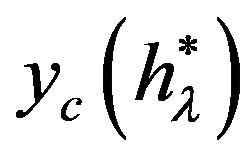
, is equal to zero
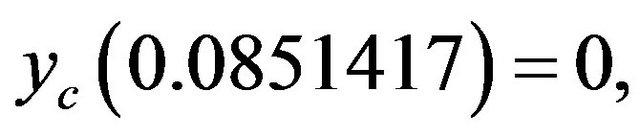has the minimum
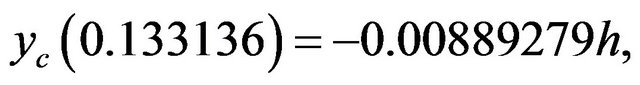and monotonically increases on the interval 
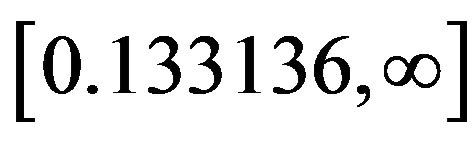reaching the value 
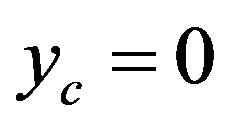only at the point 
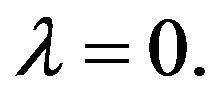If we continue to con-
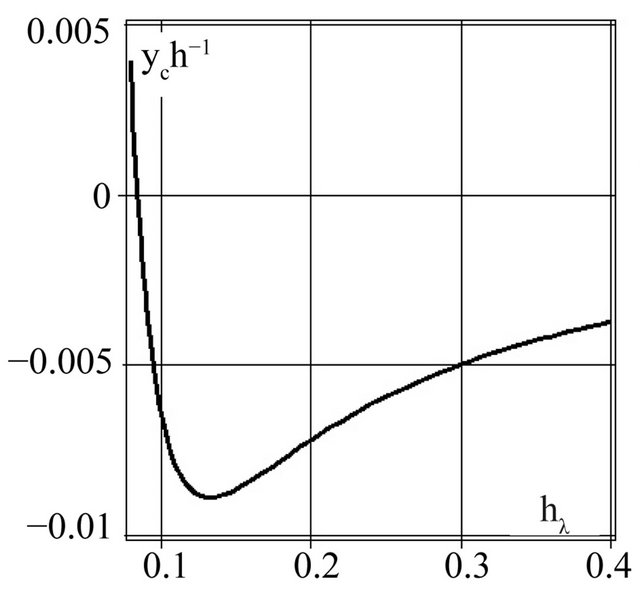
Figure 2. The dependence ych−1(hλ) for 0.08 ≤ hλ ≤ 0.4.
sider the wave behaving as a compound pendulum then it is stable at 
and unstable when
In particular let’s consider a wave of length λ = 1000 m on the surface of a fluid with depth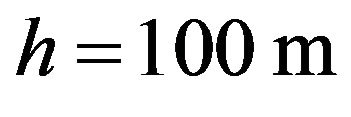 
and density 
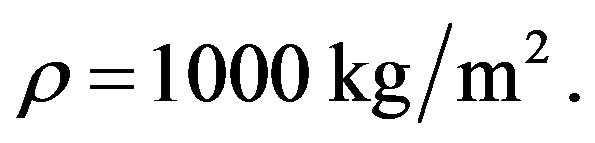The solution of system (1.3) at the point 
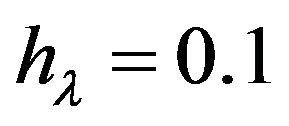(see [2]) and the coefficients b1, b2, …, b7 are given below: μ7(0.1) = 7.449619; a1 = 0.047452; a2 = 0.0195554; a3 = 0.00606262; a4 = 0.00183319; a5 = 0.000565461; a6 = 0.000178475; a7 = 0.0000568810; b1 = 0.047452; b2 = 0.0206812; b3 = 0.00700837; b4 = 0.00233431; b5 = 0.000787255; b6 = 0.000268797; b7 = 0.0000921207. Using these outcomes in Formulas (2.1)-(2.10) we get the parameters of the wave: the crest coordinate 
the trough coordinate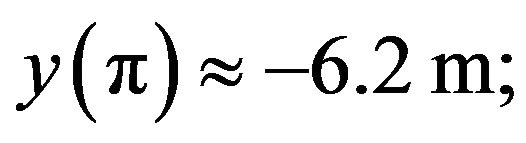 
the amplitude 
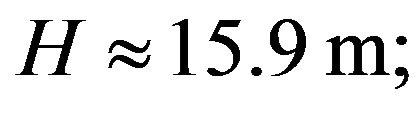the coordinates of mass center 
the kinetic energy 
the potential energy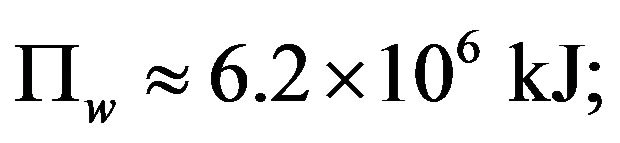 
the velocity 
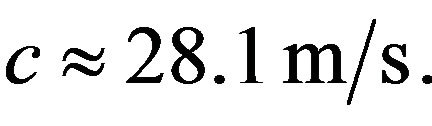This wave similar to a tsunami is stable as 
For 
and 
(The solution of the system (1.3) and coefficients 
for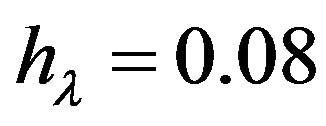 
are given in [2]) the wave parameters will be: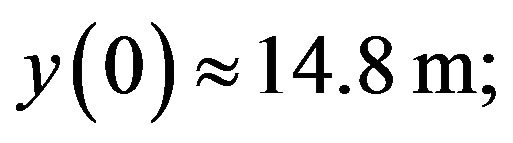 
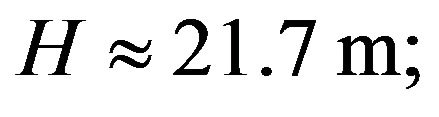
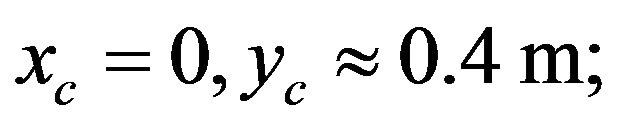
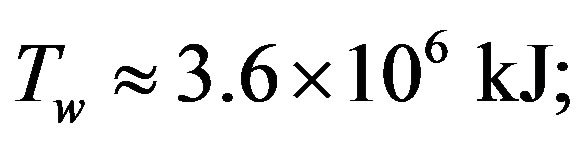
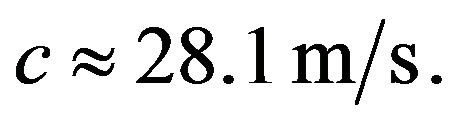This wave is unstable as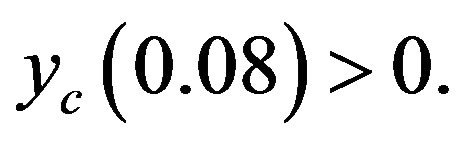 
In summary it is necessary to note that in the accessible publications we have not discovered materials for comparison, except [6].
4. Conclusion
Solving the Nekrasov’s integral equation we avoided the “Liapunov-Schmidt” method and other methods of searching the solution in the neighbourhood of eigenvalues of Nekrasov’s linearized equation. We sought the solution of this equation in the neighbourhood of the motionless point of the nonlinear integral Equation (1.5). This is the point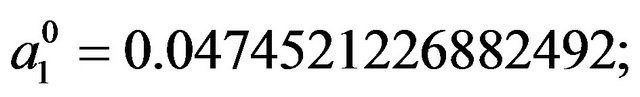 
.
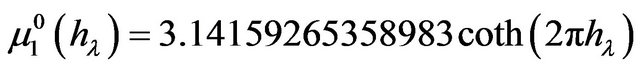