Multiple Solutions for a Class of Concave-Convex Quasilinear Elliptic Systems with Nonlinear Boundary Condition ()
1. Introduction
In this article, we are interested in the existence of two nontrivial nonnegative solutions of the following problem:

(1.1)
where  is a bounded domain with smooth boundary,
is a bounded domain with smooth boundary,  is the critical Sobolev exponent for the embedding
is the critical Sobolev exponent for the embedding .
.

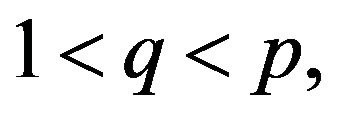 is the outer normal derivative,
is the outer normal derivative,
 , the weight m(x) is a positive bounded function and
, the weight m(x) is a positive bounded function and  are smooth functions which may change sign in Ω. By Nehari manifold, fibering method and analytic techniques, the existence of multiple positive solutions to this equation is verified.
are smooth functions which may change sign in Ω. By Nehari manifold, fibering method and analytic techniques, the existence of multiple positive solutions to this equation is verified.
In recent years, there have been many papers concerned with the existence and multiplicity of positive solutions for semilinear elliptic problems. Some interesting results can be found in Garcia-Azorero et al. [1], Wu [2-4] and the references therein. More recently, Hsu [5] has considered the following elliptic system:
 (1.2)
(1.2)
By variational methods, he proved that problem (1.2) has at least two positive solutions if the pair of the parameters  belongs to a certain subset of
belongs to a certain subset of . However, as far as we know, there are few results of problem (1.1) in addition to concave-convex nonlinearities, i.e.,
. However, as far as we know, there are few results of problem (1.1) in addition to concave-convex nonlinearities, i.e.,  , including nonlinear boundary condition. We focus on the existence of at least two nontrivial nonnegative solutions for problems (1.1) in the present paper.
, including nonlinear boundary condition. We focus on the existence of at least two nontrivial nonnegative solutions for problems (1.1) in the present paper.
Set
 (1.3)
(1.3)
where  satisfy
satisfy
 (1.4)
(1.4)
The main result of this paper is summarized in the following theorem.
Theorem 1.1. If the parameters  satisfy
satisfy

then problem (1.1) has at least two solutions 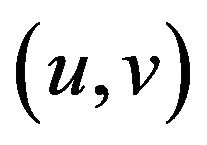 and
and  satisfy
satisfy  in
in  and
and 
It should be mentioned that the similar results about the existence of multiplicity of positive solutions for the Laplace problem with critical growth and sublinear perturbation have been discussed in the recent paper [6-8] and the reference therein.
This paper is organized as follows. Some preliminaries and properties of the Nehair manifold are established in Sections 2, and Theorems 1.1 is proved in Sections 3.
2. Preliminaries
Let  denotes the usual Sobolev space. In the Banach space
denotes the usual Sobolev space. In the Banach space  we introduce the norm which is equivalent to the standard one:
we introduce the norm which is equivalent to the standard one:

First, we give the definition of the weak solution of (1.1).
Definition 2.1. We say that  is a weak solution to (1.1) if for all
is a weak solution to (1.1) if for all , we have
, we have


It is clear that problem (1.1) has a variational structure. Let  be the corresponding energy functional of problem (1.1), and it is defined by
be the corresponding energy functional of problem (1.1), and it is defined by

where


It is not difficult to verify that the functional I is not bounded neither from below nor from above. So it is convenient to consider I restricted to a natural constraint, the Nehari manifold, that contains all the critical points of I. First we introduce the following notation: for any functional  we denote by
we denote by  the Gateaux derivative of F at
the Gateaux derivative of F at  in the direction of
in the direction of  and
and


Define the Nehari manifold
 . Note that N contains all solutions of (1.1) and
. Note that N contains all solutions of (1.1) and  if and only if
if and only if
 (2.1)
(2.1)
Lemma 2.1.  is coercive and bounded below on N.
is coercive and bounded below on N.
Proof. Suppose  From (2.1), the Holder inequality and the Sobolev embedding theorem, it follows that
From (2.1), the Holder inequality and the Sobolev embedding theorem, it follows that
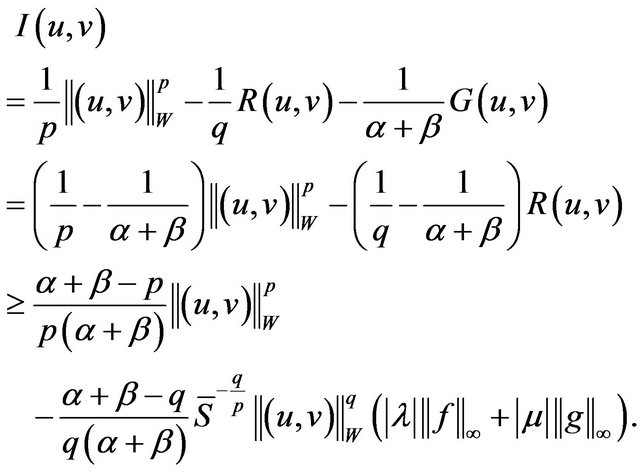 (2.2)
(2.2)
Thus  is coercive and bounded below on
is coercive and bounded below on  since
since  Define
Define  Then for all
Then for all  we have
we have
 (2.3)
(2.3)
Arguing as that in [9,10], we split  into three parts:
into three parts:



Lemma 2.2. Suppose is a local minimizer of
is a local minimizer of  on
on  and
and  Then
Then  in
in 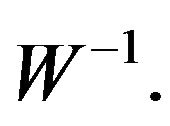
Proof. If  is a local minimizer for I on N, then
is a local minimizer for I on N, then  is a solution of the optimization problem minimize
is a solution of the optimization problem minimize  subject to
subject to

Hence, by the theory of Lagrange multipliers, there exists  such that
such that
 in
in .
.
Here  is the dual space of the Sobolev space
is the dual space of the Sobolev space . Thus,
. Thus,

But  since
since  Hence
Hence 
Lemma 2.3.  for all
for all

Proof. We argue by contradiction. Suppose that for all
 there is
there is
 then (2.3) and the Sobolev embedding theorem imply that
then (2.3) and the Sobolev embedding theorem imply that
 (2.4)
(2.4)
and

(2.5)
Thus from (2.4), (2.5) we have
 (2.6)
(2.6)
and

Consequently,

which is a contradiction.
By Lemma 2.3, we can write  for all
for all

Define
 .
.
Lemma 2.4. (i)  for all
for all

(ii) There exists a positive constant d0 depending on 
 such that
such that  for all
for all

Proof. (i) Suppose , then we have
, then we have

for 
Thus we get that 
(ii) Suppose

and . Then (2.4) implies that
. Then (2.4) implies that
 (2.7)
(2.7)
and (2.5) implies that
 (2.8)
(2.8)
From (2.7) and (2.8) it follows that


which shows that

since 
where  is a positive constant.
is a positive constant.
For all  such that
such that , set
, set

Lemma 2.5. Suppose that

and  is a function satisfying
is a function satisfying 
(i) If , then there exists a unique
, then there exists a unique 
such that  and
and  .
.
(ii) If , then there exist
, then there exist 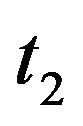 and
and  such that
such that

Furthermore, 

Proof. Fix  with
with  For all
For all , let
, let

then it is obvious that Ψ(0) = 0, Ψ(t) → −∞ as t → +∞,  as
as  small enough. So we can deduce that Ψ′(t) = 0 at
small enough. So we can deduce that Ψ′(t) = 0 at  for
for ,
,  for
for 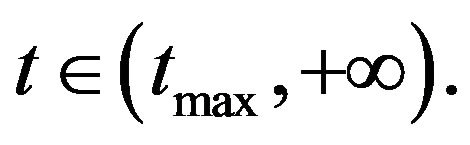 Then Ψ(t) that achieves its maximum at
Then Ψ(t) that achieves its maximum at  is increasing for
is increasing for  and decreasing for
and decreasing for  Moreover,
Moreover,

(i) If , then there exists a unique
, then there exists a unique  such that
such that  Note that
Note that

thus we get 
From

we have . For all
. For all  it follows that
it follows that



So we get that 
(ii) If  for
for


then there exist  and
and  such that
such that
 and
and
 By the similar argument in (i), we get
By the similar argument in (i), we get  and
and

 for
for 
 for
for 
Then it follows that


The proof of this Lemma is completed.
For each  with
with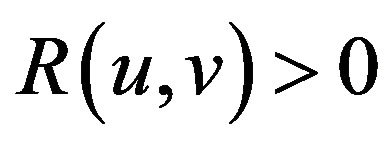 , we write
, we write
 (2.9)
(2.9)
Lemma 2.6. Suppose that

and  is a function satisfying
is a function satisfying .
.
(i) If  then there exists a unique
then there exists a unique 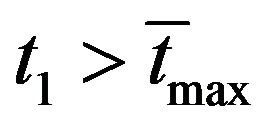 such that
such that  and
and

(ii) If , then there exist
, then there exist  and
and  such that
such that  and
and . Furthermore,
. Furthermore,


Proof. Fix  with
with  For all
For all  let
let
 (2.10)
(2.10)
then it is obvious that . So we can deduce that
. So we can deduce that  at
at 

 for
for .
.
Then  that achieves its maximum at
that achieves its maximum at  is increasing for
is increasing for  and decreasing for
and decreasing for
 Using the similar argument in Lemma 2.5, we can obtain the result of Lemma 2.6.
Using the similar argument in Lemma 2.5, we can obtain the result of Lemma 2.6.
3. Proof of Theorem 1.1
Lemma 3.1. Suppose that

then the functional has a minimizer
has a minimizer  and it satisfies
and it satisfies
(i) 
(ii)  is a nontrivial solution of (1.1).
is a nontrivial solution of (1.1).
Proof. Let be a minimizing sequence such that
be a minimizing sequence such that
 (3.1)
(3.1)
Since I is coercive on N, we get that  is bounded on
is bounded on . Passing to a subsequence (still denoted by
. Passing to a subsequence (still denoted by ), there exists
), there exists  such that
such that
 weakly in
weakly in ,
,
 a.e. in
a.e. in , (3.2)
, (3.2)
 strongly in
strongly in  and in
and in . This implies
. This implies
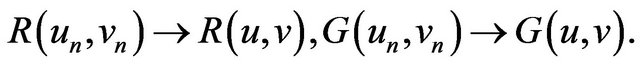
Since , we get
, we get

By Lemma 2.4 (i) we get  and then
and then . Now we prove that
. Now we prove that 
strongly in 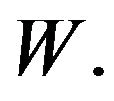 Suppose otherwise, then either
Suppose otherwise, then either
 (3.3)
(3.3)
Fix  with
with . Let
. Let
 , where
, where  is as in (2.10).
is as in (2.10).
Clearly,  as
as , and
, and
 as
as  Since
Since
 by an argument similar to the one in the proof of Lemma 2.6, we have that the function
by an argument similar to the one in the proof of Lemma 2.6, we have that the function  achieves its maximum at
achieves its maximum at , is increasing for
, is increasing for  and decreasing for
and decreasing for  where
where  is as in (2.9). Since
is as in (2.9). Since  by Lemma 2.6, there is unique
by Lemma 2.6, there is unique  such that
such that

Then
 (3.4)
(3.4)
By (3.3) and (3.4), we obtain  for n sufficiently large for the sequence
for n sufficiently large for the sequence  Since
Since
 we have
we have  Moreover,
Moreover,

and  is increasing for
is increasing for . This implies
. This implies  for all
for all 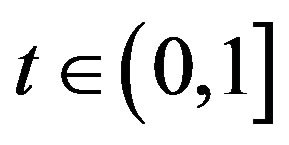 and
and  sufficiently large. We obtain
sufficiently large. We obtain . But
. But 
and  this implies
this implies

which is a contradiction. Hence  strongly in W. This implies
strongly in W. This implies 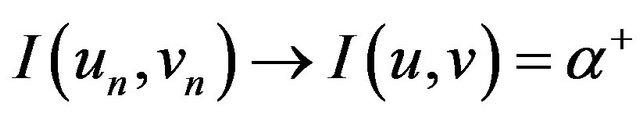 as
as . Thus
. Thus  is a minimizer for
is a minimizer for  on
on  Since
Since
 and
and , by Lemma 2.2 we may assume that
, by Lemma 2.2 we may assume that  is a nontrivial nonnegative solution of Equation (1.1).
is a nontrivial nonnegative solution of Equation (1.1).
Next we prove  Arguing by contradiction, without loss of generality, we may assume that v ≡ 0. Then as u is a nonzero solution of
Arguing by contradiction, without loss of generality, we may assume that v ≡ 0. Then as u is a nonzero solution of
 (3.5)
(3.5)
we have
 (3.6)
(3.6)
Choose  such that
such that
 (3.7)
(3.7)
then

By Lemma 2.6, there is a unique  such that
such that . Moreover, from (3.6) and (3.7), it follows that
. Moreover, from (3.6) and (3.7), it follows that

and

This implies

which contradict with that (u,0) is the minimizer and hence . So
. So is a nontrivial nonnegative solution of Equation (1.1).
is a nontrivial nonnegative solution of Equation (1.1).
Lemma 3.2. Suppose that

Then the functional  has a minimizer
has a minimizer  and it satisfies
and it satisfies
(i) 
(ii)  is a nontrivial solution of (1.1).
is a nontrivial solution of (1.1).
Proof. Let  be a minimizing sequence such that
be a minimizing sequence such that
 (3.8)
(3.8)
Since I is coercive on N, we get that  is bounded on
is bounded on . Passing to a subsequence (still denoted by
. Passing to a subsequence (still denoted by ), there exists
), there exists  such that
such that
 weakly in
weakly in ,
,
 a.e. in
a.e. in , (3.9)
, (3.9)
 strongly in
strongly in  and in
and in 
This implies

Moreover, by (2.3) we obtain
 then
then  Now we prove that
Now we prove that
 strongly in W. Suppose otherwise, then either
strongly in W. Suppose otherwise, then either
 (3.10)
(3.10)
By Lemma 2.6, there is unique to such that
 Since
Since
 for all
for all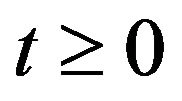 , we have
, we have

and this is a contradiction. Hence 
strongly in W. This implies 
as . Thus
. Thus 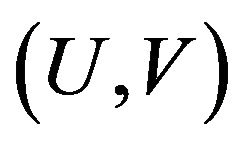 is a minimizer for I on
is a minimizer for I on .
.
Since  and
and , by Lemma 2.4 and the similar argument as that in Lemma 3.1 we can get
, by Lemma 2.4 and the similar argument as that in Lemma 3.1 we can get  is also a nontrivial nonnegative solution of Equation (1.1).
is also a nontrivial nonnegative solution of Equation (1.1).
Proof of Theorem 1.1. From Lemma 3.1 and Lemma 3.2, we obtain that Equation (1.1) has two nontrivial nonnegative solutions  and
and  satisfy
satisfy
 and
and . It remains to show that the solutions found in Lemma 3.1 and Lemma 3.2 are distinct. Since
. It remains to show that the solutions found in Lemma 3.1 and Lemma 3.2 are distinct. Since  this implies that
this implies that  and
and  are distinct. This concludes the proof.
are distinct. This concludes the proof.
4. Acknowledgements
The author is indebted to the referees for carefully reading this paper and making valuable comments and suggestions.