Convergence of Invariant Measures of Truncation Approximations to Markov Processes ()
1. Introduction
Let  be the stable, conservative
be the stable, conservative  of a continuous-time Markov process on a countable state space
of a continuous-time Markov process on a countable state space  The
The  satisfies
satisfies
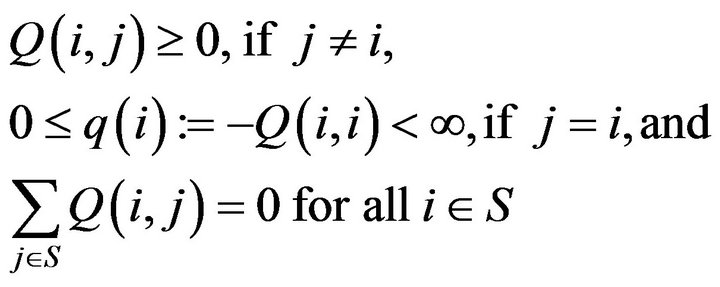
In addition, we assume that Q is regular, which means there exists no non-trivial, non-negative solution
 to
to

for some (and then all)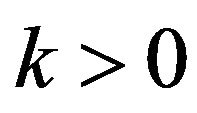 .
.
Under these assumptions, the state transition probabilities of the process are given by the unique Q-function  which satisfies the Kolmogorov backward equations,
which satisfies the Kolmogorov backward equations,
 The object
The object , which is also called a transition function, is a family of
, which is also called a transition function, is a family of  matrices indexed over the reals which constitutes an analytic semi-group. an analytic semi-group is characterised by three properties:
matrices indexed over the reals which constitutes an analytic semi-group. an analytic semi-group is characterised by three properties:  is the identity matrix, the row sums of
is the identity matrix, the row sums of  are less than or equal to unity and
are less than or equal to unity and  is equal to the matrix product
is equal to the matrix product  for all
for all . This last property, known as the Chapman-Kolmogorov equation, implies
. This last property, known as the Chapman-Kolmogorov equation, implies . Thus, even though Ft is generally thought of as the matrix of state transition probabilities at time t, it serves as an analogue to the t-th power of the transition matrix of a discrete-time Markov chain on the state space
. Thus, even though Ft is generally thought of as the matrix of state transition probabilities at time t, it serves as an analogue to the t-th power of the transition matrix of a discrete-time Markov chain on the state space  Consequently, using the superscript to denote
Consequently, using the superscript to denote as a function of t should not cause any confusion. While on the subject of notation, we should mention that we are using a standard notation common in the literature of continuous-time Markov processes on general state spaces. In the discrete state space setting, this notation causes matrices to look like functions of two variables (or kernels) while measures and vectores appear to be functions over the state space. We have elected to follow this notation in an endeavour to reduce the number of subscripts and superscripts in the sequel.
as a function of t should not cause any confusion. While on the subject of notation, we should mention that we are using a standard notation common in the literature of continuous-time Markov processes on general state spaces. In the discrete state space setting, this notation causes matrices to look like functions of two variables (or kernels) while measures and vectores appear to be functions over the state space. We have elected to follow this notation in an endeavour to reduce the number of subscripts and superscripts in the sequel.
Note that in the conservative setting posed here, regularity of  is equivalent to honesty and uniqueness of the transition function, that is,
is equivalent to honesty and uniqueness of the transition function, that is,  for all
for all 
The state space  is irreducible if
is irreducible if  for all
for all . On such a state space, a Markov process is said to be positive recurrent or ergodic if
. On such a state space, a Markov process is said to be positive recurrent or ergodic if  for all
for all  as
as . For a positive recurrent process, it can be shown (for example, see Theorem 5.1.6 in [1]) that the
. For a positive recurrent process, it can be shown (for example, see Theorem 5.1.6 in [1]) that the  satisfies
satisfies
 (1)
(1)
More generally, any measure  satisfying (1) is called an invariant or stationary measure for the process. If, in addition, the measure has mass 1, it is referred to as a stationary or invariant distribution. Any measure satisfying (1) with “
satisfying (1) is called an invariant or stationary measure for the process. If, in addition, the measure has mass 1, it is referred to as a stationary or invariant distribution. Any measure satisfying (1) with “ ” replaced by “
” replaced by “ ” is called a subinvariant measure for
” is called a subinvariant measure for . Conversely, if F has a stationary distribution
. Conversely, if F has a stationary distribution , then the process is positive recurrent and
, then the process is positive recurrent and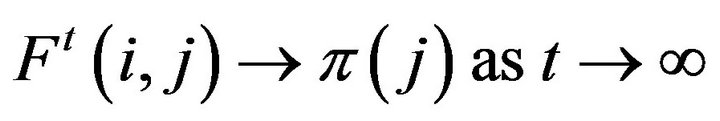 .
.
In this paper, we are interested in approximating  using the
using the 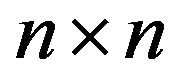 north-west corner truncations of
north-west corner truncations of . The analogous problem for discrete-time Markov chains has been studied in [2-7]. The final reference contains a review of the literature on the discrete-time version of the truncation problem. Some properties of truncation in continuous-time Markov processes were studied in [8,9].
. The analogous problem for discrete-time Markov chains has been studied in [2-7]. The final reference contains a review of the literature on the discrete-time version of the truncation problem. Some properties of truncation in continuous-time Markov processes were studied in [8,9].
Truncations of Q are submatrices of Q defined by
 , where
, where 
and  is an increasing sequence of subsets of S such that
is an increasing sequence of subsets of S such that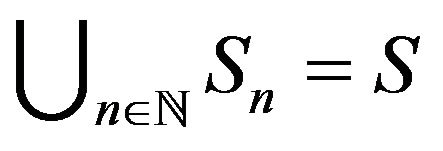 .
.
The truncation 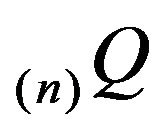 is not conservative. By adding the discarded transition rates to
is not conservative. By adding the discarded transition rates to , we may produce a conservative
, we may produce a conservative 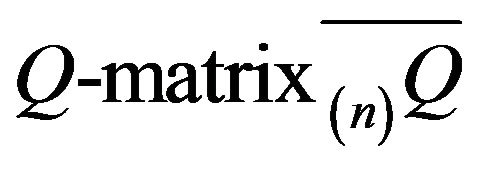 which generates a uniquehonest, finite, continuous-time Markov process. For example, we may choose to perform linear augmentation, where the aggregate of the transition rates outside of
which generates a uniquehonest, finite, continuous-time Markov process. For example, we may choose to perform linear augmentation, where the aggregate of the transition rates outside of 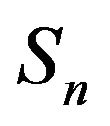 is dispersed amongst the states in
is dispersed amongst the states in  according to some probability measure
according to some probability measure . Then, the
. Then, the
 order augmentation
order augmentation  is given by
is given by

An important example of this is where we only augment a single column, say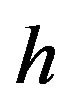 , in which case
, in which case  is the Dirac measure at h and we obtain The
is the Dirac measure at h and we obtain The  order augmentation
order augmentation  as
as

Here,  denotes the kronecker delta.
denotes the kronecker delta.
Linear augmentation obtains exactly one irreducible, closed class  together with zero or more open classes from which An is accessible. Since
together with zero or more open classes from which An is accessible. Since  is closed,
is closed,
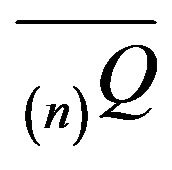 is conservative on
is conservative on  and so the minimal
and so the minimal
 is honest and positive recurrent on
is honest and positive recurrent on
 . Finiteness of
. Finiteness of  ensures that the remaining open classes are transient. Hence, there exists a unique invariant measure for
ensures that the remaining open classes are transient. Hence, there exists a unique invariant measure for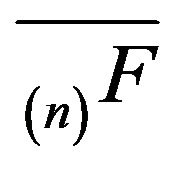 . We shall be mainly concerned with
. We shall be mainly concerned with  where either
where either  or
or . The minimal
. The minimal 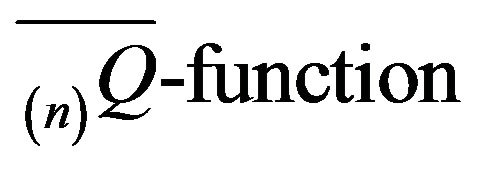 will be denoted
will be denoted  while
while
 will be its invariant probability measure.
will be its invariant probability measure.
Two obvious questions now arise. Firstly, when does
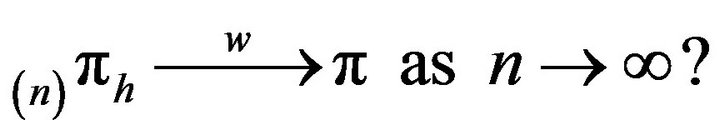 (2)
(2)
Here, we use  to denote convergence in total variation norm. Secondly, how quickly does this convergence occur? This paper considers the first question. We shall present augmentation strategies for approximating invariant distributions for two classes of Markov processes via
to denote convergence in total variation norm. Secondly, how quickly does this convergence occur? This paper considers the first question. We shall present augmentation strategies for approximating invariant distributions for two classes of Markov processes via  for n large. The classes are:
for n large. The classes are:
• Markov processes which satisfy

for some . Such processes are called exponentially ergodic.
. Such processes are called exponentially ergodic.
• Stochastically monotone Markov processes, which have the property that

for all , and processes dominated by stochastically monotone processes.
, and processes dominated by stochastically monotone processes.
Parallelling results for discrete-time chains in [7], we shall also show that Markov processes constructed from finite perturbations of stochastically monotone processes are always dominated by some other stochastically monotone process. This extends the class of processes for which our results are applicable.
In the next section, we begin by showing that the limit of the  is unique when it exists. Then, Section 3 considers exponentially ergodic Markov processes while Section 4 studies stochastically monotone Markov processes and their above-mentioned variations.
is unique when it exists. Then, Section 3 considers exponentially ergodic Markov processes while Section 4 studies stochastically monotone Markov processes and their above-mentioned variations.
Finally, some concluding remarks are made in Section 5.
2. Preliminaries
The problem of proving that  may be broken into two parts. Firstly we must show that
may be broken into two parts. Firstly we must show that  converges weakly to some limit, say
converges weakly to some limit, say , and secondly, that
, and secondly, that . We consider the latter in this section.
. We consider the latter in this section.
Theorem 2.1 Consider a sequence of linearly augmented  derived from Q and let
derived from Q and let
 be the minimal
be the minimal  -function. Then
-function. Then
 (3)
(3)
Proof: Let  denote the minimal
denote the minimal 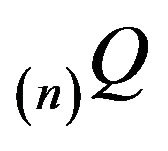 -function.
-function.
Firstly, observe that  for all
for all
 and
and . This can be seen inductively using the backward integral recurrences for
. This can be seen inductively using the backward integral recurrences for  and
and . The argument parallels the proof of Theorem 2.2.14 in [1] which states that
. The argument parallels the proof of Theorem 2.2.14 in [1] which states that
 (4)
(4)
for all 
Next, since  is honest and
is honest and 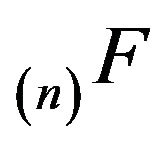 is dishonest, we see that
is dishonest, we see that
 (5)
(5)
for , where
, where
 (6)
(6)
Applying (4) to (6) together with monotone convergence shows that  monotonically decreases to 0 as
monotonically decreases to 0 as . Taking limits in n on both sides of (5) then completes the proof.
. Taking limits in n on both sides of (5) then completes the proof.
Remark 2.2 Although we have only considered linear augmentations, the statement and proof of Theorem 2.1 is in fact valid for any sequence of augmentations
 .
.
Since the transition function  is finite, it is positive recurrent on some subset of
is finite, it is positive recurrent on some subset of . Hence it possesses a unique stationary distribution
. Hence it possesses a unique stationary distribution  and
and
 (7)
(7)
for . Positive recurrence establishes anequivalence between the stationary distributions for
. Positive recurrence establishes anequivalence between the stationary distributions for  and invariant distributions for
and invariant distributions for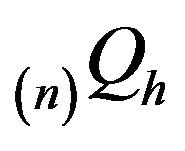 . An invariant distribution for an arbitrary
. An invariant distribution for an arbitrary  is any probability measure
is any probability measure  such that
such that  for all
for all
 . So,
. So,  uniquely satisfies
uniquely satisfies
 for all
for all 
Let us assume for the moment that  converges weakly to some limit measure
converges weakly to some limit measure . We require that
. We require that . Weak convergence to
. Weak convergence to  implies that
implies that  is a probability distribution. By taking the limit infimum on both sides of (7) and applying Fatou’s Lemma, we have
is a probability distribution. By taking the limit infimum on both sides of (7) and applying Fatou’s Lemma, we have

for . The measure
. The measure  is therefore a subinvariant probability measure for
is therefore a subinvariant probability measure for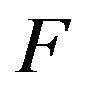 . However,
. However, 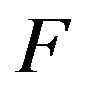 is positive recurrent and hence, by Theorem 4 in [10],
is positive recurrent and hence, by Theorem 4 in [10],  is both invariant and the unique probability measure satisfying (1). Hence,
is both invariant and the unique probability measure satisfying (1). Hence, .
.
3. Exponential Ergodicity
Let Q be the  of a positive recurrent Markov process
of a positive recurrent Markov process 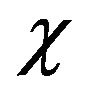 on
on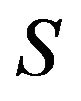 . Consider an increasing sequence of sets
. Consider an increasing sequence of sets 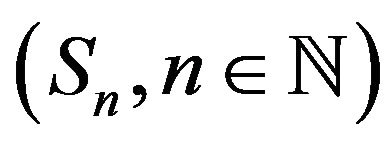 such that
such that 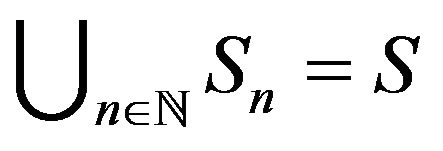 and
and 
for all n. Let  be the truncation of
be the truncation of  corresponding to
corresponding to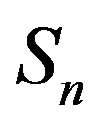 . In this section, we shall consider augmentations
. In this section, we shall consider augmentations 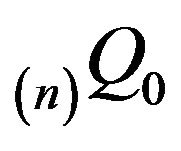 obtained by linearly augmenting
obtained by linearly augmenting  in column 0. We shall prove that exponential ergodicity of the Markov process is sufficient for
in column 0. We shall prove that exponential ergodicity of the Markov process is sufficient for  as
as  where
where  is taken to be
is taken to be , the invariant distribution for
, the invariant distribution for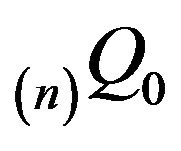 . In order to do this, we shall require the notion of a
. In order to do this, we shall require the notion of a  -norm. Let
-norm. Let be an arbitrary vector (function) such that
be an arbitrary vector (function) such that  for all
for all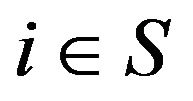 . In future, we abreviate this to
. In future, we abreviate this to . The
. The 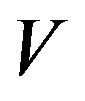 - norm of a signed measure n is then
- norm of a signed measure n is then

If  is a matrix, then the
is a matrix, then the 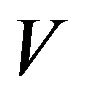 -norm of
-norm of  is
is

Rather than working with the Q-matrix augmentationsdirectly, we will use the 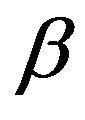 -resolvents associated with these. The
-resolvents associated with these. The  -resolvent of a continuoust-time Markov process is the stochastic matrix
-resolvent of a continuoust-time Markov process is the stochastic matrix
 given by,
given by,
 We note that
We note that  satisfies the resolvent forms of both the backward and forward equations which are
satisfies the resolvent forms of both the backward and forward equations which are  and
and  respectively.
respectively.
Since  is regular,
is regular, 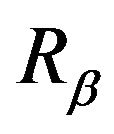 is the unique solution to the resolvent form of the backward equations. Let
is the unique solution to the resolvent form of the backward equations. Let  and
and  denote the unique
denote the unique  -resolvents of
-resolvents of  and
and  respectively. Here,
respectively. Here, 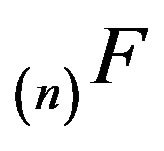 is the minimal
is the minimal 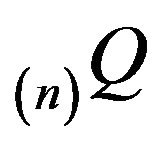 -funcction while
-funcction while 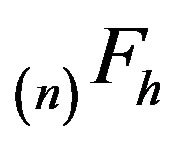 denotes the minimal
denotes the minimal  - function. Since
- function. Since  is a finite set,
is a finite set,  ,
,  and
and  have the same invariant distribution
have the same invariant distribution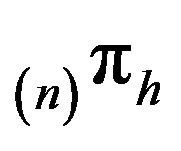 . The same is true for
. The same is true for  and
and , which share the distribution
, which share the distribution .
.
In the sequel, we shall have need of the following corollary to Theorem 2.1.
Corollary 3.1
i. For all ,
,
 (8)
(8)
where ; and ii.
; and ii.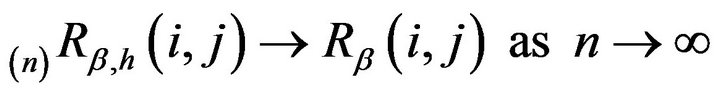 .
.
Proof: Part i is obtained by integrating both sides of (5) with respect to be . Part ii then follows by taking limits in (8) and observing that
. Part ii then follows by taking limits in (8) and observing that
 and
and 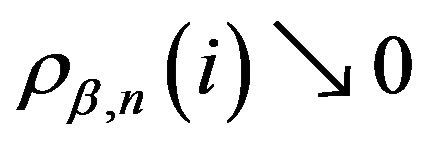 as
as 
Next, the various “drift to C” conditions introduced in [11] will play an important role in allowing us to pass between the continuous-time process and the discretetime  -resolvent chain. The drift conditions require the notion of a petite set in both continuoustime processes and discrete-time chains. Let
-resolvent chain. The drift conditions require the notion of a petite set in both continuoustime processes and discrete-time chains. Let  denote the Borel
denote the Borel  -algebra on S. Then, A set
-algebra on S. Then, A set 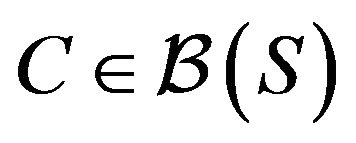 is a petite set in the continuous-time setting if there exists a probability distribution
is a petite set in the continuous-time setting if there exists a probability distribution 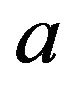 on
on  and a non-trivial positive measure
and a non-trivial positive measure  such that
such that
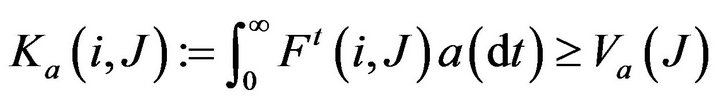
for , where
, where .
.
Petite sets for discrete-time chains are defined analogously. According to Theorem 5.1 in [11], the following three drift conditions are equivalent, although the petite set C and function V may differ in each instance.
 : Drift for T-skeletons. For some
: Drift for T-skeletons. For some , there exist constants
, there exist constants 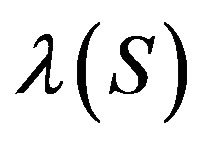 bounded for all
bounded for all  with
with , together with a petite set
, together with a petite set  and a function
and a function  such that
such that

for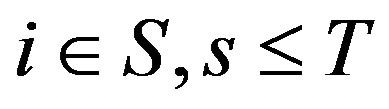 . We use
. We use 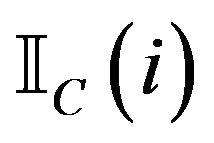 to denote the indicator function of the set C which is 1 if
to denote the indicator function of the set C which is 1 if  and 0 otherwise.
and 0 otherwise.
 : Drift for
: Drift for  -resolvents. For some
-resolvents. For some
 , a petite set
, a petite set 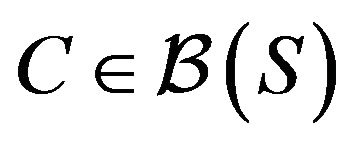 and a function
and a function

 : Drift for the Q-matrix. For constants
: Drift for the Q-matrix. For constants 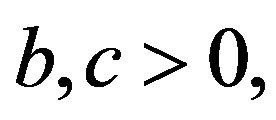 a petite set
a petite set  and a function
and a function 

An irreducible continuous-time Markov process X is  -uniformly ergodic if, for some invariant probability kernel
-uniformly ergodic if, for some invariant probability kernel . In the special case where
. In the special case where , the chain is said to be uniformly ergodic or strongly ergodic: For all
, the chain is said to be uniformly ergodic or strongly ergodic: For all  as
as 
where, by an abuse of notation, we use  to denote the invariant transition kervnel
to denote the invariant transition kervnel  for all
for all 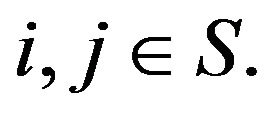
The following theorem collects together a number of results on exponential and  -uniform ergodicity of Markov processes from the literature.
-uniform ergodicity of Markov processes from the literature.
Theorem 3.2 Let X be an irreducible, aperiodic continuous-time Markov process on S. The following conditions are equivalent.
i. One of the drift conditions  holds, in which case they all hold, but not necessarily with the same petite set
holds, in which case they all hold, but not necessarily with the same petite set ;
;
ii. For all , the T-skeleton chain is geometrically ergodic;
, the T-skeleton chain is geometrically ergodic;
iii. For all , the
, the  -resolvent chain is geometrically ergodic;
-resolvent chain is geometrically ergodic;
iv. X is exponentially ergodic.
v. X is  -uniformly ergodic for some
-uniformly ergodic for some .
.
In particular, it is  -uniformly ergodic,
-uniformly ergodic, 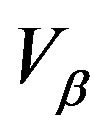 -uniformly ergodic and
-uniformly ergodic and  -uniformly ergodic where
-uniformly ergodic where  and
and 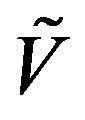 satisfy
satisfy  respectively.
respectively.
Proof:
ii iii
iii iv. This was proved in Theorem 5.3 of [11].
iv. This was proved in Theorem 5.3 of [11].
i iv. Theorem 5.1 of [11] shows that
iv. Theorem 5.1 of [11] shows that
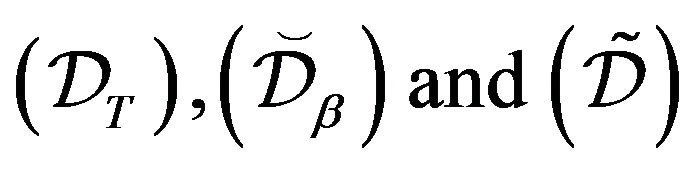 satisfy a solidarity property in that either all of them hold or none hold. Next, fix
satisfy a solidarity property in that either all of them hold or none hold. Next, fix  and set
and set  which is trivialy petite Since it is finite. In
which is trivialy petite Since it is finite. In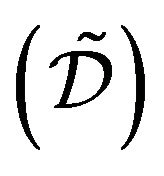 , set
, set 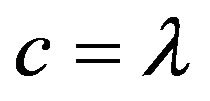 and
and , where
, where
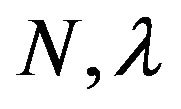 and the
and the ’s are those appearing in Theorem 3 of [12]. Finally, an appropriate relabelling of the states in
’s are those appearing in Theorem 3 of [12]. Finally, an appropriate relabelling of the states in
 reveals
reveals  to be equivalent to the necessary and sufficient condition for exponential ergodicity givenin Part (ii) of Theorem 3 in [12]. Consequently X is exponentially ergodic if and only if
to be equivalent to the necessary and sufficient condition for exponential ergodicity givenin Part (ii) of Theorem 3 in [12]. Consequently X is exponentially ergodic if and only if  orany of the other drift criteria holds.
orany of the other drift criteria holds.
i v. Theorem 5.2 in [11] says that any of
v. Theorem 5.2 in [11] says that any of  is sufficient for X to be
is sufficient for X to be 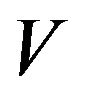 -uniformly ergodic where
-uniformly ergodic where  is either
is either  or
or  respectively.
respectively.
v ii. If X is
ii. If X is -uniformly ergodic for some
-uniformly ergodic for some , then so to is the
, then so to is the 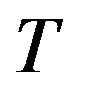 - skeleton for any
- skeleton for any  and an application of Theorem 16.0.1 in [13] shows that
and an application of Theorem 16.0.1 in [13] shows that
 for some
for some  and
and .
.
Geometric ergodicity of the 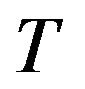 -skeleton
-skeleton 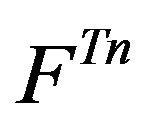 then follows from the definition of the
then follows from the definition of the  -norm.
-norm.
Next, suppose that the Markov process X is exponenttially ergodic. From Theorem 3.2, there exist constants  and a function
and a function  such that
such that
 (9)
(9)
Without loss of generality, we may take  and assume that
and assume that . The state space can always be relabelled to accommodate this convention. Then, since
. The state space can always be relabelled to accommodate this convention. Then, since  for all
for all , the augmented
, the augmented  -matrices
-matrices  each satisfy
each satisfy

Multiplying both sides by  and re-arranging, we obtain
and re-arranging, we obtain
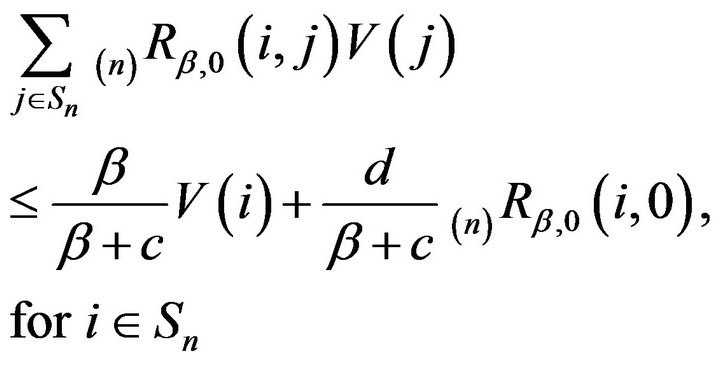 .
.
Now, choose  such that
such that
 for some
for some
 . This is always possible since
. This is always possible since  is a strictly positive matrix (in particular,
is a strictly positive matrix (in particular,  and, as noted in the proof of Corollary 3.1,
and, as noted in the proof of Corollary 3.1,
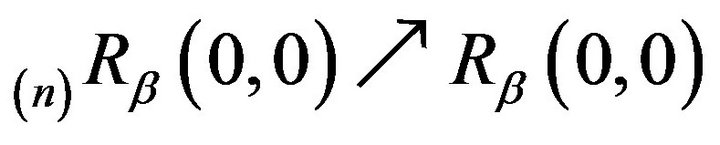 as
as . Therefore,
. Therefore,
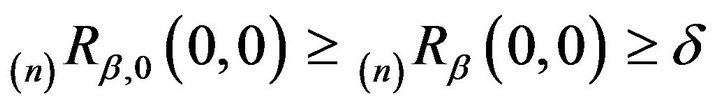 . So, in addition to
. So, in addition to 
being strongly aperiodic, we see that  is strongly aperiodic for all
is strongly aperiodic for all . A transition matrix is strongly aperiodic if it is primative and possesses a non-zero diagonal entry.
. A transition matrix is strongly aperiodic if it is primative and possesses a non-zero diagonal entry.
Define . By Proposition 5.5.4 in [13], the set
. By Proposition 5.5.4 in [13], the set  is petite since the singleton set
is petite since the singleton set  is trivially petite and
is trivially petite and  is uniformly accessible from
is uniformly accessible from  under the resolvent chain
under the resolvent chain , that is,
, that is,
 is bounded away from 0 for all
is bounded away from 0 for all . By the definition of
. By the definition of , we have
, we have  for
for
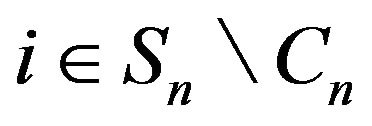 . On the other hand,
. On the other hand,  for
for
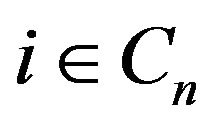 , since
, since  is a stochastic matrix. Hence we have
is a stochastic matrix. Hence we have
 (10)
(10)
 (11)
(11)
where 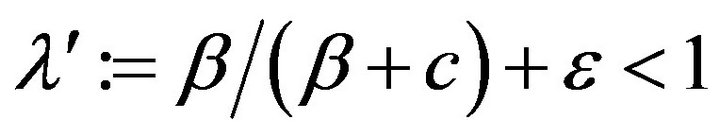 and
and .
.
Note that  for all
for all  large enough.
large enough.
Next, set 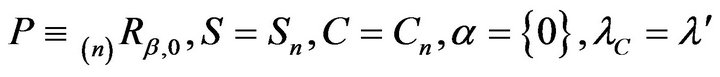 and
and  in Theorem 6.1 of [14]. It can be seen that the conditions of the theorem are satisfied and so there exists some
in Theorem 6.1 of [14]. It can be seen that the conditions of the theorem are satisfied and so there exists some  such that
such that
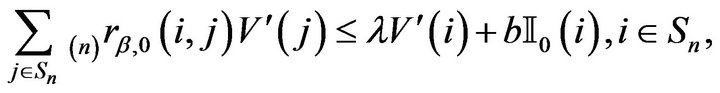
where  and
and
 . Furthermore, we have
. Furthermore, we have

where 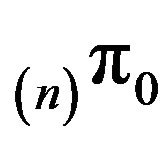 is the unique invariant distribution for
is the unique invariant distribution for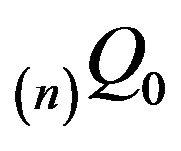 , and
, and  and
and 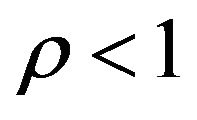 are completely determined by
are completely determined by  and
and . Note that this is true for every
. Note that this is true for every  so that the rate of convergence
so that the rate of convergence  is independent of the truncation size. In addition, by applying the preceding argument directly to
is independent of the truncation size. In addition, by applying the preceding argument directly to instead of
instead of , we also have
, we also have  for all m, sinceby assumption, (9) holds and
for all m, sinceby assumption, (9) holds and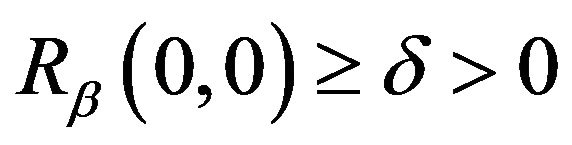 . Thus, not only are
. Thus, not only are  and
and  V-uniformly ergodic, they are geometrically ergodic with the same convergence rate
V-uniformly ergodic, they are geometrically ergodic with the same convergence rate .
.
We can now prove the main result of this section.
Theorem 3.3 Let X be an exponentially ergodic, continuous-time Markov chain on a countable, irreducible state space . Let
. Let  and
and 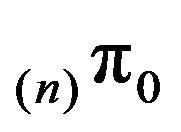 be the invariant distributions for
be the invariant distributions for  and
and 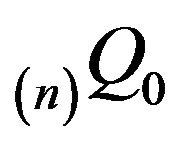 respectively. Then,
respectively. Then,
 as
as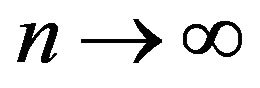 .
.
Proof: Choose an arbitrary number . From the triangle inequality, we have
. From the triangle inequality, we have
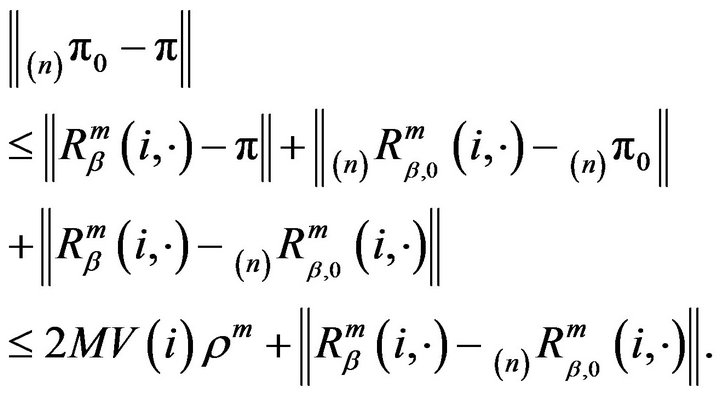 (13)
(13)
As was pointed out in [7], if  and
and 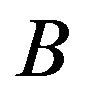 are two stochastic matrices, then
are two stochastic matrices, then
 (14)
(14)
for . Applying this to the last term in (13), we obtain
. Applying this to the last term in (13), we obtain
 (15)
(15)
where

Now, since  as
as  for all
for all , we can use dominated convergence to conclude that the third term in (13) vanishes as n tends to infinity. Thus,
, we can use dominated convergence to conclude that the third term in (13) vanishes as n tends to infinity. Thus,

for , and since m was chosen arbitrarily,
, and since m was chosen arbitrarily,
 .
.
Example
Let  and define
and define  by
by

The process with this  -matrix is essentially a renewal process with renewal times marked by visits to state 0. Each renewal time consists of a geometric number of exponential times of mean
-matrix is essentially a renewal process with renewal times marked by visits to state 0. Each renewal time consists of a geometric number of exponential times of mean  followed by an exponential time of mean
followed by an exponential time of mean . At each jump, the process passes from state
. At each jump, the process passes from state to state
to state with probability
with probability  and falls back to state 0 with probability
and falls back to state 0 with probability . the state space is clearly irreducible and the process has a geometric stationary distribution
. the state space is clearly irreducible and the process has a geometric stationary distribution , where
, where . Existence of the stationary distribution ensures positive recurrence.
. Existence of the stationary distribution ensures positive recurrence.
Next, let the vector  be given by
be given by , where
, where . Also define
. Also define  and Set
and Set
 , where c is a small positive number. Then, the drift condition
, where c is a small positive number. Then, the drift condition  holds for the specified
holds for the specified  and
and . The process is therefore exponentially ergodic by Theorem 3.2. Further, all the conditions of Theorem 3.3 are satisfied. Thus, we can construct augmentations
. The process is therefore exponentially ergodic by Theorem 3.2. Further, all the conditions of Theorem 3.3 are satisfied. Thus, we can construct augmentations  on corresponding sets
on corresponding sets 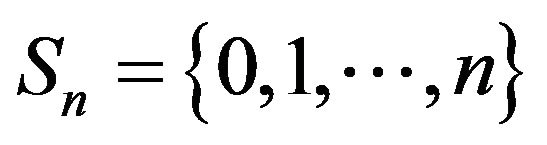 and use their invariant distributions
and use their invariant distributions  to approximate
to approximate .
.
We can confirm this by solving
 with
with
 . We have
. We have 
for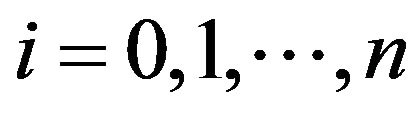 , from which it is evident that
, from which it is evident that
( as
as . Convergence in total variation follows by the same argument used later in the proof of Theorem 4.2.
. Convergence in total variation follows by the same argument used later in the proof of Theorem 4.2.
4. Stochastic Monotonicity
In this section, we develop results for stochastically monotone Markov processes. Our key result says that stochastic monotonicity of the process is sufficient for (2) to hold under arbitrary linear augmentation. The remaining results extend this to larger classes of Markov processes. While our methods generally parallel those employed in [6] TO study the same problem in discrete-time Markov chains, itt is necessary to take greater care constructing the augmentations in the continuous-time setting.
Let 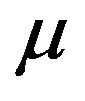 and
and  be two non-trivial measures. Then,
be two non-trivial measures. Then, 
stochastically dominates  if
if 
for all , in which case we write
, in which case we write . If
. If  and
and  are two transition functions, we say that
are two transition functions, we say that  stochastically dominates
stochastically dominates 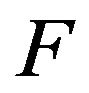 (written
(written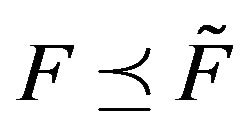 ) if, for all
) if, for all 
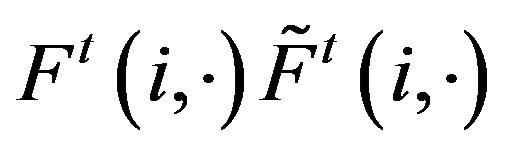 for all
for all  A more strict classification is stochastic comparability. The transition functions
A more strict classification is stochastic comparability. The transition functions  and
and  are stochastically comparable if
are stochastically comparable if  for all
for all  and
and  with
with  We use the notation
We use the notation  to mean that
to mean that  and
and 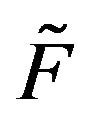 are stochastically comparable. A stochastically monotone Markov process is one whose transition function is stochastically comparable to itself. Thus, if
are stochastically comparable. A stochastically monotone Markov process is one whose transition function is stochastically comparable to itself. Thus, if 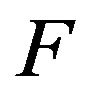 is stochastically dominated by a transition function
is stochastically dominated by a transition function  which itself is stochastically monotone, then
which itself is stochastically monotone, then  and
and  are stochasticallly comparable. Clearly,
are stochasticallly comparable. Clearly,  implies
implies 
The following theorem is the key to obtaining sufficient conditions for (2) to hold in continuous time. It characterises stochastic comparability and monotonicity in terms of -matrix structure and is a special case of a more general result which was proved in [15] (also see Theorem 7.3.4 in [1] for an account). The reader is directed to the last two citations for the proof.
-matrix structure and is a special case of a more general result which was proved in [15] (also see Theorem 7.3.4 in [1] for an account). The reader is directed to the last two citations for the proof.
Theorem 4.1 ([15] and [1, Chapter 7.3])
i. Let  and
and  be two conservative
be two conservative  -matrices. Their corresponding minimal transition functions
-matrices. Their corresponding minimal transition functions  and
and 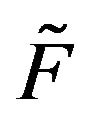 are stochastically comparable iff, whenever
are stochastically comparable iff, whenever  and k is such that either
and k is such that either  or
or  then
then
 (16)
(16)
ii. Let  be a conservative
be a conservative  -matrix. Its minimal
-matrix. Its minimal  -function F is stochastically monotone iff, Whenever
-function F is stochastically monotone iff, Whenever  and k is such that either
and k is such that either  or
or  then
then
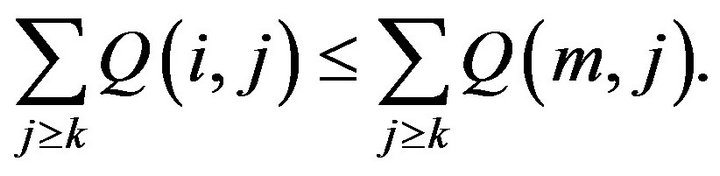 (17)
(17)
As a consequence of this result, we shall speak of stochastically monotone Q-matrices and of two Q-matrices as being stochastically comparable, etc. This abuse of terminology should not cause any confusion.
If  is an irreducible, positive recurrent transition function and it stochastically dominates another irreducible transition function
is an irreducible, positive recurrent transition function and it stochastically dominates another irreducible transition function  then
then 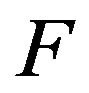 is also positive recurrent. Furthermore, if
is also positive recurrent. Furthermore, if  and
and  denote the stationary distributions of F and
denote the stationary distributions of F and  respectively, then
respectively, then  which can be seen by letting
which can be seen by letting  in
in

In fact, we may say something stronger than this. If  is reducible and contains a collection of closed ireducible classes
is reducible and contains a collection of closed ireducible classes 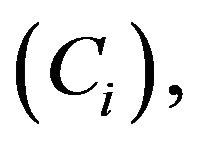 each Ci is positive recurrent with invariant probability measure
each Ci is positive recurrent with invariant probability measure  Since F is dominated by
Since F is dominated by  on
on  it follows that
it follows that  Now, any invariant measure on
Now, any invariant measure on  for
for  can be written as a linear combination of the
can be written as a linear combination of the ’s; that is,
’s; that is, 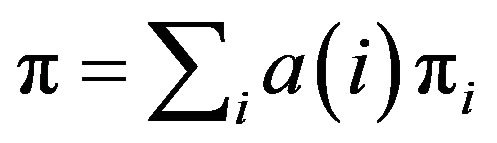 for some probability measure
for some probability measure  Therefore,
Therefore,  for all invariant distributions
for all invariant distributions .
.
Throughout the rest of this section, we shall use the north-west corner truncations of  that is, truncations of the form
that is, truncations of the form 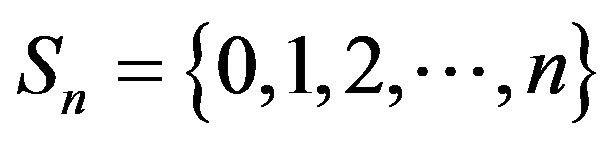 for
for 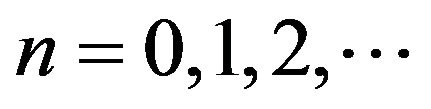
4.1. Stochastically Monotone Processes
Let  be the
be the  -matrix of a positive recurrent, stochastically monotone Markov process F. By construction, the
-matrix of a positive recurrent, stochastically monotone Markov process F. By construction, the  north-west corner truncations of
north-west corner truncations of  augmented in the nth column are stochastically monotone. Since
augmented in the nth column are stochastically monotone. Since  is conservative on a finite set
is conservative on a finite set 
 has precisely one positive recurrent class, which contains
has precisely one positive recurrent class, which contains  and is a subset of or equal to
and is a subset of or equal to  Its limiting distribution
Its limiting distribution  satisfies
satisfies 
for all  From Theorem 4.1, we also see that
From Theorem 4.1, we also see that  is stochastically monotone.
is stochastically monotone.
Let  be an arbitrary augmentation of
be an arbitrary augmentation of  and note that
and note that  is stochastically comparable with
is stochastically comparable with  As per our comments above, the minimal
As per our comments above, the minimal 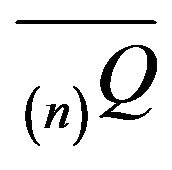 -function
-function 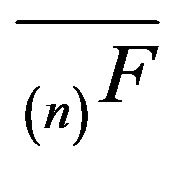 is positive recurrent on one or more irreducible subsets of
is positive recurrent on one or more irreducible subsets of  and hence any invariant distribution for
and hence any invariant distribution for
 , say
, say  is stochastically dominated by
is stochastically dominated by 
Now, let us extend  and
and  to S as follows:
to S as follows:
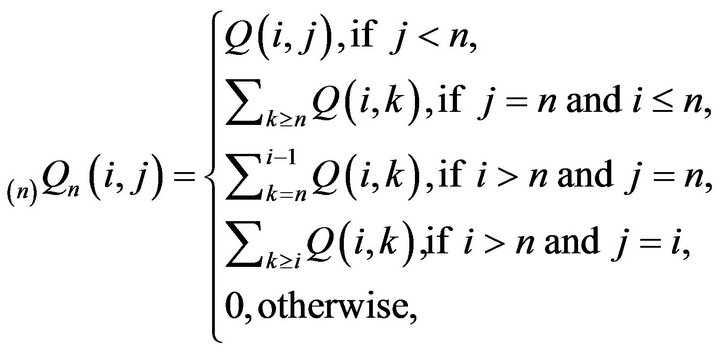 (18)
(18)
and
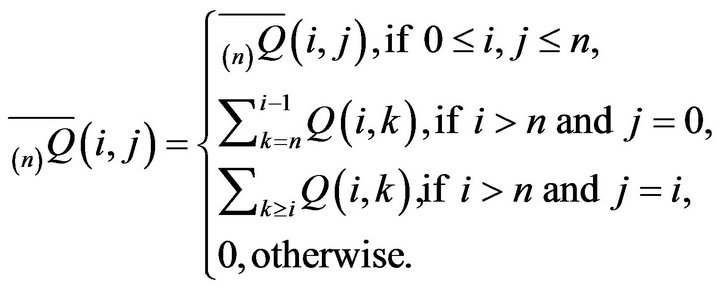
We also extend 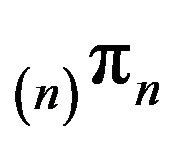 and
and 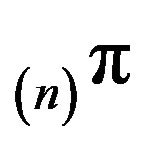 to
to  by appending a countably infinite number of 0’s to each, so that
by appending a countably infinite number of 0’s to each, so that  for all
for all  Note that
Note that 
(resp. ) remains invariant for
) remains invariant for 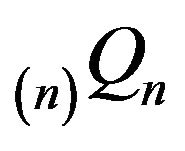 (resp.
(resp. ).
).
Moreover, since the minimal  -function
-function  is positive recurrent on some subset of
is positive recurrent on some subset of 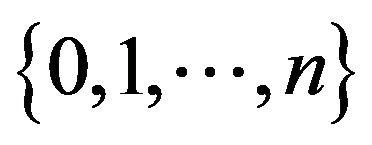 containing n and transient elsewhere in
containing n and transient elsewhere in  the measure
the measure  is the limiting distribution of
is the limiting distribution of
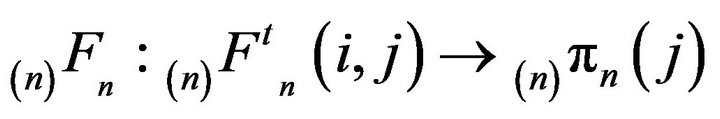 as
as  for all
for all
 Similarly,
Similarly,  is the limiting distribution for the minimal
is the limiting distribution for the minimal  -function
-function 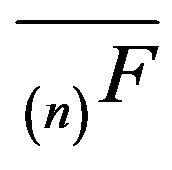 when given an appropriate initial distribution.
when given an appropriate initial distribution.
The stochastically monotone matrix  dominates
dominates
 while
while  and
and  are stochastically comparable for all
are stochastically comparable for all  So too are
So too are  and
and
 for all
for all  Thus,
Thus, 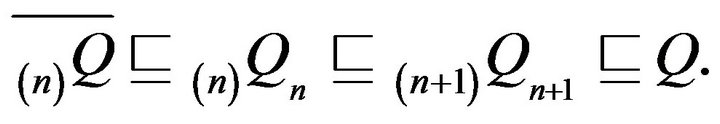 An application of Part i of Theorem 4.1 then shows that
An application of Part i of Theorem 4.1 then shows that  for all
for all  Consquently,
Consquently,
 (19)
(19)
where  is the unique stationary distribution for
is the unique stationary distribution for  The sequence
The sequence 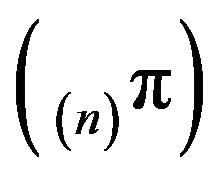 is therefore tight and so
is therefore tight and so
 for all
for all  as
as  The same is true for
The same is true for 
From (19), we observe that
 for all
for all
 and so
and so  is at least as good an approximation to p as
is at least as good an approximation to p as . Thus, any invariant measure derived from a north-west corner truncation of
. Thus, any invariant measure derived from a north-west corner truncation of  augmented in its last column is optimal for approximating
augmented in its last column is optimal for approximating .
.
As was pointed out in [7], the pointwise convergence of measures on a countable set can easily be extended to convergence in total variation. We therefore have the following result.
Theorem 4.2 Let  be the
be the  -matrix of a positive recurrent, stochastically monotone Markov process on
-matrix of a positive recurrent, stochastically monotone Markov process on  Let p be the stationary distribution of the minimal
Let p be the stationary distribution of the minimal  -function
-function  and denote the invariant distribution of an arbitrary
and denote the invariant distribution of an arbitrary  north-west corner augmentation
north-west corner augmentation
 by
by 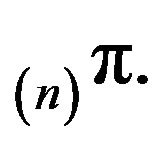 Furthermore, let
Furthermore, let  be the
be the 
north-west corner truncation augmented in column n and take 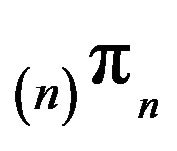 to be its invariant distribution. Then,
to be its invariant distribution. Then,
 as
as  The same is true of the sequence
The same is true of the sequence  which is the optimal approximation in the sense that its tail mass more closely approximates that of
which is the optimal approximation in the sense that its tail mass more closely approximates that of .
.
Proof: The fact that, for all 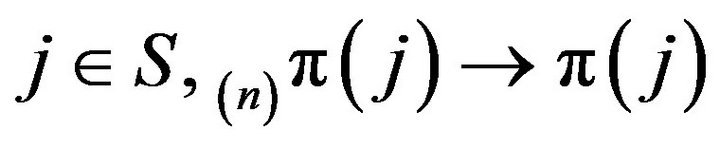 and
and  as
as  was established in the preceding discussion. So too was the optimality of
was established in the preceding discussion. So too was the optimality of  as an approximation to
as an approximation to  To prove convergence in total variation, fix an arbitrary finite
To prove convergence in total variation, fix an arbitrary finite  Then, we obtain
Then, we obtain

The analogous statement holds for  and the proof is completed by letting first
and the proof is completed by letting first  and then
and then  tend to infinity.
tend to infinity.
As remarked in [6], 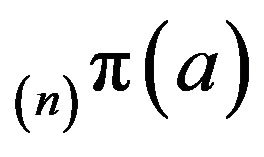 will be strictly positive for sufficiently large n where a is an arbitrary state in
will be strictly positive for sufficiently large n where a is an arbitrary state in  Thus,
Thus,  contains a positive recurrent class to which n belongs. Computationally speaking, this means that any invariant distribution will suffice as an approximation to
contains a positive recurrent class to which n belongs. Computationally speaking, this means that any invariant distribution will suffice as an approximation to , provided n is sufficiently large.
, provided n is sufficiently large.
Finally, if n is large enough so that  possesses a quasistationary distribution (n)r supported on a nondegenerate irreducible subset of
possesses a quasistationary distribution (n)r supported on a nondegenerate irreducible subset of  then the sequence of distributions
then the sequence of distributions  converges weakly to
converges weakly to  We can always find a sequence
We can always find a sequence 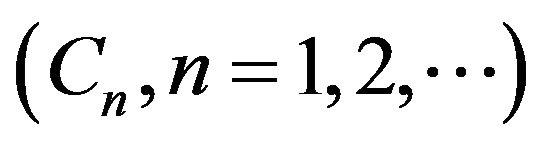 of irreducible sets such that
of irreducible sets such that  and
and 
See Lemma 5.1 in [16] for a proof of this; the analogue for discrete-time Markov chains may be found in [3], Theorem 3.1.
For a finite state Markov process, every quasistationary distribution is equivalent to a probabilitynormalised left eigenvector of its  -matrix restricted to an ireducible class. In other words, If
-matrix restricted to an ireducible class. In other words, If  is a nonconservative
is a nonconservative  -matrix on a finite state space S containing an ireducible class
-matrix on a finite state space S containing an ireducible class  is a quasistationary distribution on C for the process if and only if
is a quasistationary distribution on C for the process if and only if  and, for some
and, for some 
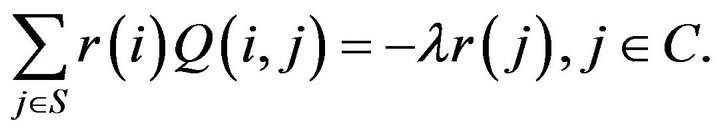
Note that by virtue of  -theory,
-theory, 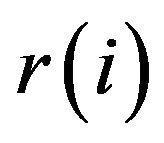 is strictly positive for all
is strictly positive for all 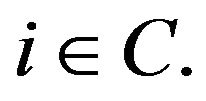 By convention, we extend r to
By convention, we extend r to  by setting
by setting 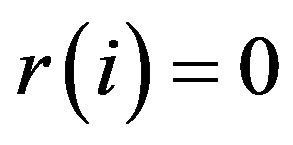 for
for  If we then construct the linear augmentation
If we then construct the linear augmentation  as
as
 (20)
(20)
 it is not difficult to see that the invariant distribution
it is not difficult to see that the invariant distribution  for
for  is unique and equivalent to
is unique and equivalent to 
Now, let us return to the case of a countably infinite state space. Given n large, we may construct  from
from
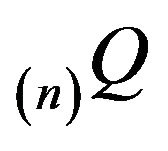 in the same manner as (20) using a left eigenvector
in the same manner as (20) using a left eigenvector  of
of 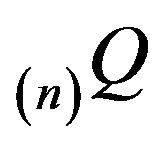 supported on an irreducible class
supported on an irreducible class  The conditions of Theorem 4.2 are satisfied and so the sequence
The conditions of Theorem 4.2 are satisfied and so the sequence  converges in total variation to the invariant distribution of
converges in total variation to the invariant distribution of  This observation subsumes results concerning the truncation approximation of invariant distributions of birth-death processes and subcritical Markov branching processes, for example, see [16-18]. The convergence of quasistationary distributions of truncations to the invariant distribution of the original process also holds under the weaker conditions we discuss in the next two subsections.
This observation subsumes results concerning the truncation approximation of invariant distributions of birth-death processes and subcritical Markov branching processes, for example, see [16-18]. The convergence of quasistationary distributions of truncations to the invariant distribution of the original process also holds under the weaker conditions we discuss in the next two subsections.
4.2. Processes Dominated by Stochastically Monotone Processes
Now we shall consider a much larger class of Markov processes, namely those whose transition functions are stochastically dominated by a positive recurrent, stochastically monotone process. To begin, let  be the stochastically monotone transition function of an irreducible, positive recurrent Markov process. Suppose that
be the stochastically monotone transition function of an irreducible, positive recurrent Markov process. Suppose that  dominates a transition function F. We shall use
dominates a transition function F. We shall use  and
and  to denote the corresponding
to denote the corresponding  -matrices. As noted earlier, F must be positive recurrent and the invariant distributions
-matrices. As noted earlier, F must be positive recurrent and the invariant distributions  and
and , corresponding to
, corresponding to  and
and  respectively, satisfy
respectively, satisfy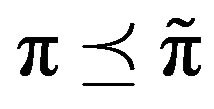 .
.
Let  and
and  respectively denote the
respectively denote the 
north-west corner truncations of  and
and 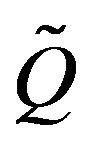 augmented in the
augmented in the  th column. By extending these in the analogous way to (18) and applying Part i of Theorem 4.1, we see that
th column. By extending these in the analogous way to (18) and applying Part i of Theorem 4.1, we see that  and
and  are stochastically comparable.
are stochastically comparable.
Also, let  be an arbitrary augmentation of an
be an arbitrary augmentation of an 
north-west corner truncation of and note that
and note that
 whence
whence  From the previous subsection,
From the previous subsection,  for
for 
Combining these, we obtain
 which implies that
which implies that
 Thus, the sequence
Thus, the sequence
 is tight and
is tight and  componentwise as
componentwise as 
Convergence in total variation follows in the same way as in the proof of Theorem 4.2 and the same is true of
 Thus we have proved the following result.
Thus we have proved the following result.
Theorem 4.3 Let  be the
be the  -matrix of an irreducible Markov process which is dominated by a positive recurrent, stochastically monotone Markov process. Then,
-matrix of an irreducible Markov process which is dominated by a positive recurrent, stochastically monotone Markov process. Then,
 as
as  where p is the unique invariant distribution for
where p is the unique invariant distribution for  and
and  for
for 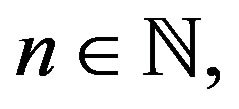 constitutes an invariant distribution of an arbitrary
constitutes an invariant distribution of an arbitrary  north-west corner augmentation of
north-west corner augmentation of 
As the augmentation  is a special case of
is a special case of 
it follows from the theorem that  as
as
 However, unlike the situation in which F is stochastically monotone, it is not clear which of
However, unlike the situation in which F is stochastically monotone, it is not clear which of  and
and  provides the better approximation to
provides the better approximation to 
4.3. Finitely Perturbed Stochastically Monotone Markov Processes
Finally, we consider an even more general class of Markov processes which was introduced in [7]. We say that Q is a finite perturbation of  if the two Q-matrices differ in at most a finite number of columns. Let
if the two Q-matrices differ in at most a finite number of columns. Let  be stochastically monotone and suppose without loss of generality that Q and
be stochastically monotone and suppose without loss of generality that Q and  differ in the first k columns. Let
differ in the first k columns. Let
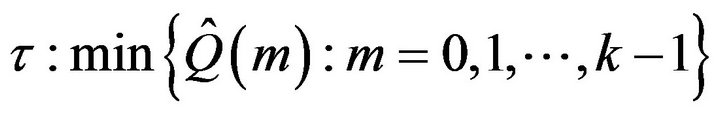 and construct a
and construct a
 as follows:
as follows:
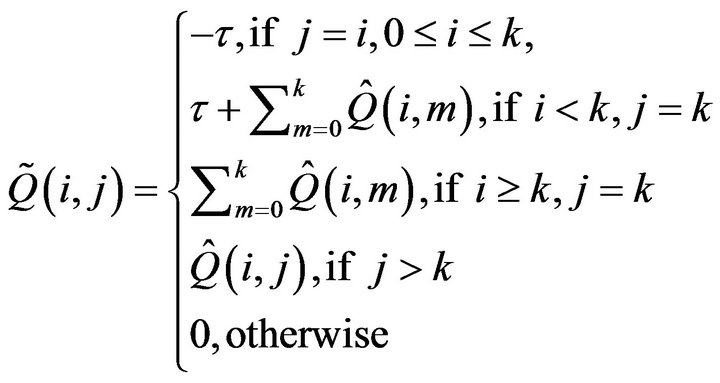
Observe that  is stochastically monotone. This is due firstly to the way in which the first k columns have been constructed from
is stochastically monotone. This is due firstly to the way in which the first k columns have been constructed from , and secondly to the agreement between the remaining columns of
, and secondly to the agreement between the remaining columns of  with the corresponding columns of the stochastically monotone
with the corresponding columns of the stochastically monotone . Now,
. Now, 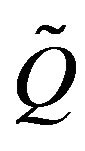 satisfies (17) and so, by Theorem 4.1, the minimal
satisfies (17) and so, by Theorem 4.1, the minimal  -function F and
-function F and -function
-function  are stochastically comparable. Direct application of Theorem 4.3 to
are stochastically comparable. Direct application of Theorem 4.3 to 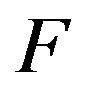 and
and 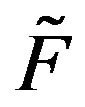 then yields the following result.
then yields the following result.
Theorem 4.4 Let  be a finite perturbation of a Qmatrix
be a finite perturbation of a Qmatrix  whose minimal
whose minimal 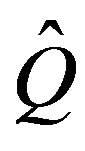 -function is irreducible, positive recurrent and stochastically monotone. Also, let p be the unique invariant distribution for
-function is irreducible, positive recurrent and stochastically monotone. Also, let p be the unique invariant distribution for  and denote the invariant distributions of arbitrary
and denote the invariant distributions of arbitrary  north-west corner augmentations
north-west corner augmentations  by
by . Then,
. Then,

4.4. Example
Conrth-death process, whose tridiagonal 
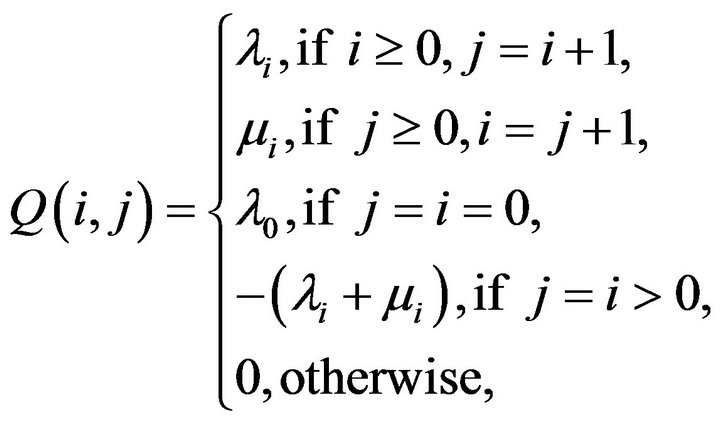
where 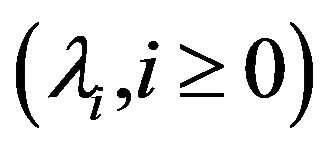 are strictly positive birth rates and
are strictly positive birth rates and
 are strictly positive death rates. Here, we take the state space S to be the set of non-negative integers. Such processes can be used to model queues having memoriless arrival and service times, simple circuitswitched teletraffic networks and buffers in computer networks, etc.
are strictly positive death rates. Here, we take the state space S to be the set of non-negative integers. Such processes can be used to model queues having memoriless arrival and service times, simple circuitswitched teletraffic networks and buffers in computer networks, etc.
Let  be the
be the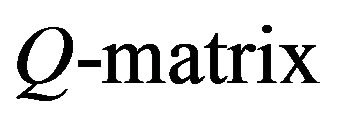 of an irreducible birth-death process. Then, it can be shown (see [1], Chapter 3) that
of an irreducible birth-death process. Then, it can be shown (see [1], Chapter 3) that
 is regular if and only if
is regular if and only if 
where  and
and  for
for . Now for
. Now for
 regular, the unique minimal transition function
regular, the unique minimal transition function  is positive recurrent if and only if
is positive recurrent if and only if  and
and . The stationary distribution for
. The stationary distribution for  is
is
 where
where 
Now, it is straight forward to verify that  satisfies (17) and hence, by Theorem 4.1,
satisfies (17) and hence, by Theorem 4.1,  is stochastically monotone. furthermore, by Theorem 4.2, we may use
is stochastically monotone. furthermore, by Theorem 4.2, we may use  to approximate
to approximate . Letting
. Letting 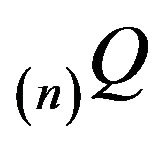 denote the north-west corner truncation on
denote the north-west corner truncation on , augmentation in column n yields the matrix
, augmentation in column n yields the matrix 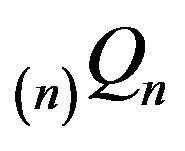 which differs from
which differs from  only in its
only in its  element. More precisely,
element. More precisely,
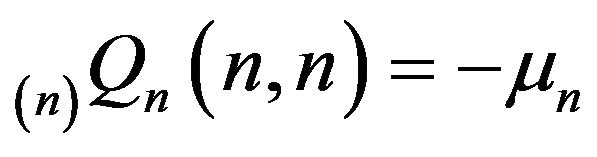 and
and if either
if either 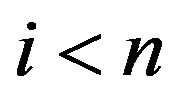 or
or . The stationary distribution
. The stationary distribution  corresponding to the augmentation
corresponding to the augmentation  is given by
is given by 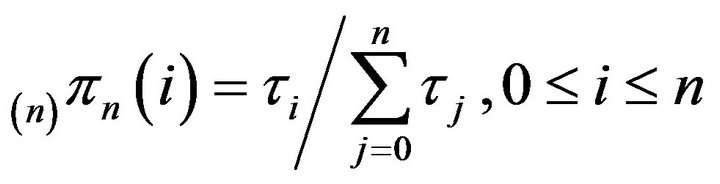 From this closed form expression, it can immediately be seen that
From this closed form expression, it can immediately be seen that
 as
as  since
since  as
as
 . Convergence in total variation then follows as in the proof of Theorem 4.2.
. Convergence in total variation then follows as in the proof of Theorem 4.2.
5. Conclusion
Here we have investigated procedures based on the augmentation of state-space truncations for approximating the stationary distributions of positive recurrent, continuous-time Markov processes on countably infinite state spaces. We have shown that approximation techniques first proposed for application to discrete-time markov chains are also efficacious in the continuous-time setting. Two classes of Markov process were considered: Exponentially ergodic processes and stochastically monotone processes. It was shown that the invariant distributions 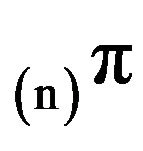 corresponding to the augmented
corresponding to the augmented
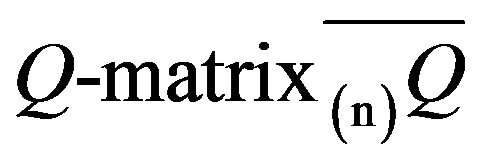 of finite statespace truncations of a
of finite statespace truncations of a
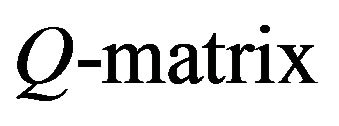 converge in total variation to the invariant distribution of the Markov process generated by that
converge in total variation to the invariant distribution of the Markov process generated by that . It remains to study the speed of such convergence. An understanding of the convergence rate would enable the truncation size to be selected in order to guarantee that the measure
. It remains to study the speed of such convergence. An understanding of the convergence rate would enable the truncation size to be selected in order to guarantee that the measure 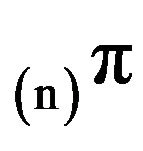 approximates
approximates  to a desired degree of accuracy.
to a desired degree of accuracy.
6. Acknowledgements
This work was supported by the Center for Mathematical Modeling (CMM) Basal CONICYT Program PFB 03 and FONDECYT grant 1070344. AGH would like to thank Servet Martinez for interesting discussion on the truncation of stochastically monotone processes. AGH dedicates this article to co-author Richard Tweedie, who passed away after this work was started.