Mathematical Modeling of the Actual Infiltration Process for the Preparation of C/C Composites ()
1. Introduction
Ceramic composites are widely used industrially because of their prominent properties. Especially, carbon/carbon composites are lighter, and have a low thermal expansion, a high thermal conductivity, and a good mechanical resistance. They can be produced by reinforcing composites with fibers by Chemical Vapor Infiltration (CVI). In the CVI process, the precursor gas diffuses into a porous preform, reacts at pore walls, and deposits matrix materials [1]. Here, deposition of pyrolytic carbon in a well defined manner is required. Hence the modeling of the real deposition process such as overturning the preform in the middle of the process is important [2]. Here, the numerical simulations were used to optimize parameter values of the actual CVI process [3].
The kinetic mechanisms of the heterogeneous carbon deposition have been proposed [4,5]. And modeling based on the detailed surface kinetic mechanism [6-8] and the active surface sites [9] were also proposed. On the other hand, a global deposition model was used when transport phenomena were taken into account [10]. Diffusion and deposition kinetics were considered [11]. Furthermore, models visualizing the deposition in the preform based on the overall deposition reaction kinetics were also proposed [12,13]. In this work, the modeling based on the overall deposition reaction kinetics proposed by Vaidyaraman [14] was developed for the visualization of the deposition profile in the preform.
The objective of this work is modeling the preparation of fiber reinforced C/C composites by F-CVI of C from propane. Time changes of pore size, porosity, and amount of deposition, etc. could be estimated. The main concerns were the effects of overturning the preform in the middle of the deposition process. How the distribution of porosity and the final average porosity change with the overturning process were calculated for the different timeinterval and the different number of overturning. The results were compared with those obtained without overturning the preform.
2. Model Development
The same modeling as used in our previous work [15] was used in this research. The only differences were the inclusions of overturning the sample in the middle of the process. For the inclusions of the overturning process in the modeling, the additional mathematical equations were not necessary. The only necessary operation was that the calculated parameter values were exchanged in the following way so that the entrance parameter values become the exit parameter values and vice versa. The following explanations for the model equations are almost same as reported in our previous work [15].
The cylindrical preform is composed of fibers which are assumed nonporous. It is also assumed that pores among fibers distributed evenly in the whole preform as shown in Figure 1.
Reactant gas, i.e., propane, flows from one side of the preform to the other by the convection in the z-direction.
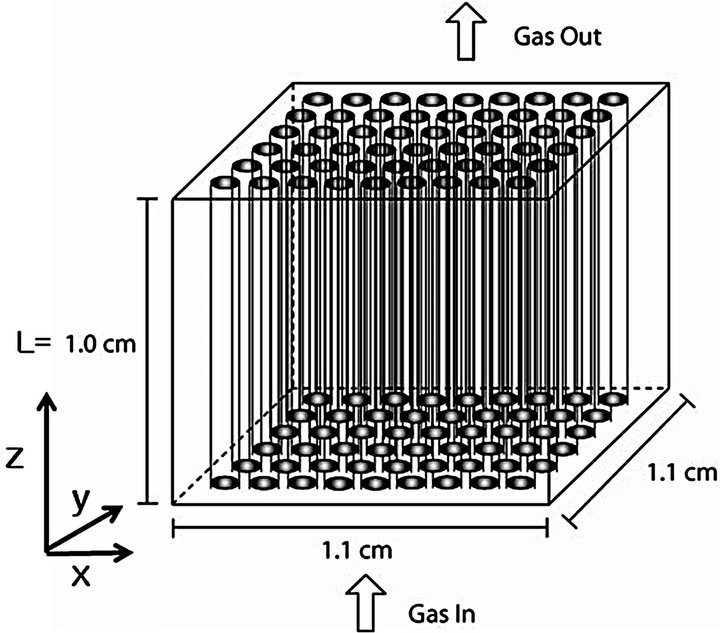
Figure 1. Schematic diagram of the perform.
It is supposed that the carbon infiltration and deposition reaction is a first order of propane concentration. One mole of propane produces 3 moles of carbon and 4 moles of hydrogen.
 (1)
(1)
The mole balance for each ingredient was made as follows.
 (2)
(2)
Here, the second item is the deposition on the outside lateral surface of fibers in the preform. The deposition rate constant (kS) reported by Vaidyaraman [14] was used.
 (3)
(3)
Here, R is the gas constant and T the reaction temperature. The momentum balance equation for the packed column was used. The equations for the changes of fiber radius (rf), the amount of deposition per unit cross-sectional area (D), and porosity ( ) at z are as follows.
) at z are as follows.
 (4)
(4)
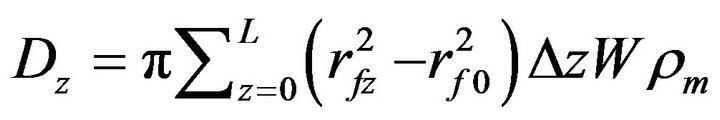 (5)
(5)
 (6)
(6)
Here, q is the mole number of deposited C from 1 mole of propane. Mm and ρm are the molecular weight and the density of deposited carbon, respectively. CAz is the concentration of propane at z and W is the number of fibers per unit cross-sectional area of perform. Time changes of fiber radius in Equation (4) were time changes of thickness of deposit around the cylindrical fiber. The amount of deposition in Equation (5) and the porosity in Equation (6) were calculated with this fiber radius.
The above equations were changed into a dimensionless form and solved by a finite difference method.
As explained above, the overturning process was included in the following way. After a certain time of deposition, the calculated parameter values were exchanged so that the entrance parameter values become the exit parameter values and vice versa.
3. Results and Discussion
Mathematical modeling was carried out with the parameter values listed in Table 1. Dimensions of the preform were taken from a sample used in the experiments done in our laboratory. In the previous work [15], CVI depositions were carried out without overturning and the modeling calculation results were fitted to the experimental data of the amount of deposition in the preform with an adjusted reaction rate constant. This adjusted reaction rate constant was used in the following work.
3.1. Deposition Rate Constant
In our previous work, comparisons of the experimental amount of deposition with the modeling calculation results were obtained as shown in Figure 2 [15]. Preforms were not overturned in the previous experiments. Symbols are experimental data and curves are modeling results. Experiments were carried out at 900˚C. When the rate constant in equation (3), reported by Vaidyaraman et al. [14], was multiplied by 2 at 100% propane and by 30 at 5%, 10%, 20% propane, the modeling results matched with the experimental data [15]. Hence modeling calculations in this research were carried out with an adjusted rate constant of 10 kS, which is the middle value between 2 kS and 30 kS.
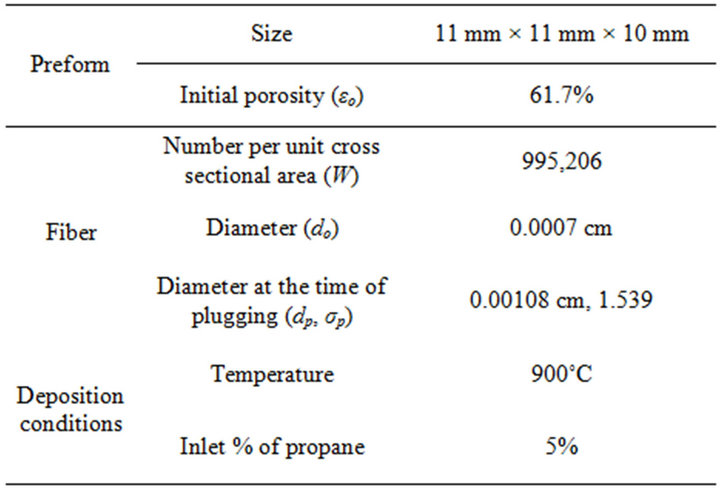
Table 1. Dimensions of the preform and deposition conditions used in the modeling.
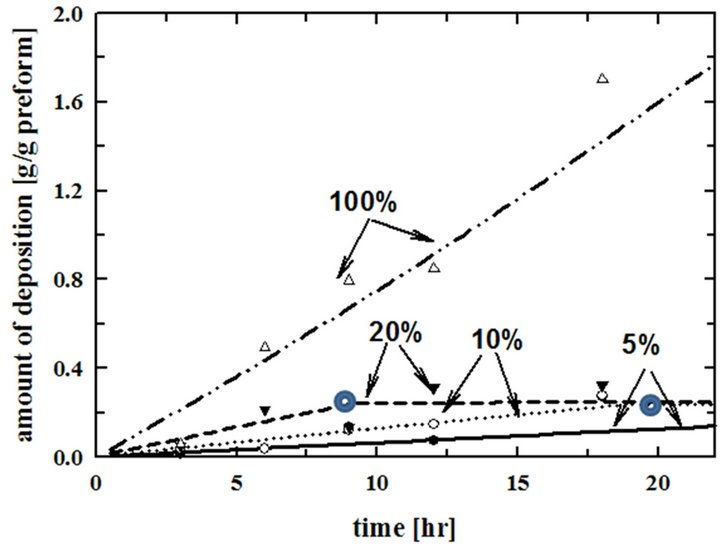
Figure 2. Comparisons of the modeling calculations with the experimental data of the amount of deposition per unit mass of the preform at different inlet percentages of propane. Modeling results were obtained by calculating with 2 kS for 100% and 30 kS for 5%, 10%, and 20% inlet propane [15]. The symbols,  , are inflection points.
, are inflection points.
The modeling calculation results in Figure 2 have inflection points. These are at the times when the pore entrances on the outside surfaces of the preform are plugged. There are no more depositions inside of the preform after those points. The surface area for the deposition on the outside of the preform is very small compared with that inside of the preform. As a result, the amount of deposition becomes very small. So the slope of the fitting curve becomes very small. This is the reason why overturning the preform in the middle of the deposition process is necessary.
3.2. Effects of Overturning during the Process
During deposition, the porosity near pore entrances decreases fast because of a high propane concentration. On the other hand, the porosity near pore exits decreases slowly because of a low propane concentration. So it is necessary to overturn the preform during a deposition process in order to reduce the porosity differences. The porosity distributions in the preform are in Figure 3 for the 3 cases of depositions a) without overturning, b) with overturning at every 30 hrs, and c) with overturning at every 10 hrs. The porosity differences between pore entrances and pore exits in the preform deposited without overturning are big. On the other hand, those porosity differences of the preform deposited with over-turning many times decreased a lot. Furthermore, the differences between porosities at the entrance and at the exit become small when the time intervals of overturning the preform are small. So there resulted more uniform depositions in the preform with the 10-hr-interval overturning than those in the preform with the 30-hr-interval overturning
 (a)
(a) (b)
(b) (c)
(c)
Figure 3. Time changes of the distributions of porosities (ε) in the preform for the different time intervals of overturning: (a) without an overturning, (b) with the 30-hr-interval, and (c) with the 10-hr-interval overturning.
in Figure 3(c). This can be seen again in Figure 4. A small time-interval overturning resulted in a uniform deposition at the time of pore plugging.
Figure 4 is the porosity distribution at the time of plugging pore entrances on the outside surfaces of the preform for the different time-intervals of overturning. As shown in Figure 3, it can be seen again that porosity differences at pore entrances and at pore exits show little differences when the time-interval of overturning the preform is small.
Time changes of the porosities at z = 0.2 L are shown in Figure 5. Since the time intervals of overturning the preform are different, the numbers of overturning are different in each case. The time of plugging pore entrances is extended as the time-intervals of overturning the preform becomes short. Additionally, the final porosities after plugging pore entrances become small.
Time changes of the average porosity and the total amount of deposition for the different time intervals of overturning the preform are shown in Figure 6. The decrease of the average porosity means the increase of the amount of deposition. It can be said that the amount of deposition done with 10 times overturning of 20-hr-interval becomes twice of that done without overturning.
3.3. Effects of Other Process Parameters
Figure 7 is the distributions of porosities in the preform (a) at 80-hr and (b) at the plugging time for the different reaction rate constants when the preforms were overturned at 30-hr-interval. Other conditions for the calculation were 900˚C, 5% inlet propane concentration, and 10 kS. A relatively uniform deposition is obtained with a small reaction rate constant as expected.