A New Full-NT-Step Infeasible Interior-Point Algorithm for SDP Based on a Specific Kernel Function ()
1. Introduction
In this paper we deal with SDP problems, whose primal and dual forms are:
and
where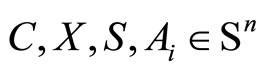
,
. The matrices
, 
are assumed to be linearly independent.
The use of Interior-Point Methods (IPMs) based on the kernel functions becomes more desirable because of the efficiency from a computational point of view. Many researchers have been attracted by the Primal-Dual IPMs for SDP. For a comprehensive study, the reader is referred to Klerk [1], Roos [2] and Wolkowicz et al. [3]. Bai et al. [4] introduced a new class of so-called eligible kernel functions for Linear Optimization (LO) which are defined by some simple properties following the same way of Peng et al. who have designed a class of IPMs based on a so-called self-regular proximities [5]. These methods use the new search directions which are different than the classic Newton directions. Some extensions were successfully made by Mansouri and Roos [6], Liu and Sun [7]. In the current paper, we propose a new infeasible interior-point algorithm, whose feasibility step is induced by a specific kernel function.
In the sequel, we denotes e as the all one vector and 
the vector of eigenvalues of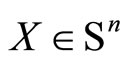
. Two different forms of norm will be used
2. The Statement of the Algorithm
We start usually with assuming that the initial iterates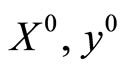 
and 
are as follows
where I is the 
identity matrix, 
is the initial dual gap and 
is such that
for some optimal solution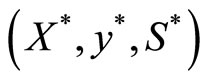 
of 
and
.
2.1. The Feasible SDP Problem
The perturbed KKT condition for 
and 
is
Based on different symmetrization schemes, several search directions have been proposed.
As in Mansouri and Roos [6], we use in this paper, the so-called NT-direction determined by the following system
(1)
where
(2)
We also define the square root matrix
.
The matrix D can be used to rescale X and S to be the same matrix V, defined by
(3)
It is clear that D and V are symmetric and positive definite. Let us further define
(4)
where
. Using the above notations, the third equation of the system (1) is then formulated as follows
(5)
It is clear that the first two equations imply that 
and 
are orthogonal, i.e.
, which yields that 
and 
are both zero if and only if
. In this case, X and S satisfy
, implying that X and S are the 
-centers. Hence, we can use the norm 
as a quantity to measure closeness to the 
-centers. Let us define
(6)
2.2. The Perturbed Problem
For any 
with
, we consider the perturbed problem
, defined by
and its dual problem 
given by
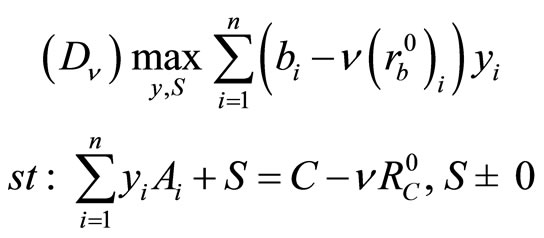
where
Note that if 
then 
and 
, yielding that both 
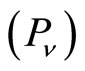and 
are strictly feasible.
Lemma 1 ([6], Lemma 4.1) Let the original problems, 
and
, be feasible. Then for each 
such that 
the perturbed problems 
and 
are strictly feasible.
We assume that 
and 
are feasible. It follows from Lemma (1) that the problems 
and 
are strictly feasible. Hence their central path exists. The central path of 
and 
is defined by the solution sets 
of the following system
If 
and
, we denote this unique solution as
. 
is the 
-center of
, and 
the 
-center of
. By taking
, one has 
. Initially, one has 
and
, whence 
and
. In what follows, we assume that at the start of each iteration,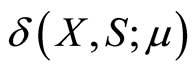 
is smaller than a threshold value 
which is obviously true at the start of the first iteration. The following system is used to define the step 
(7)
where 
and
.
Inspired by [8], we used in the third equation for the above system, a linearization
, which means that we target the 
-center of 
and
.
After the feasibility step, the new iterates are given by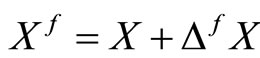
, 
and
. The algorithm begins with an infeasible interior point 
such that 
is feasible for the perturbed problems, 
and
. First we find a new point 
which is feasible for the perturbed problems with
. Then 
is decreased to
. A few centering steps are applied to produce new points 
such that
. This process is repeated until the algorithm terminates. Starting at the iterates 
and targeting the 
-center, the centering steps are obtained by solving the system (1).
2.3. Infeasible IPMs Based on a Specific Kernel Function
Now we introduce the definition of a kernel function. We call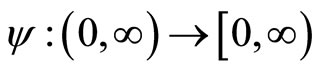 
a kernel function if 
is twice differentiable and the following conditions are satisfied
1) 
2) 
for all 
3)
.
We define
(8)
By using the scaled search directions 
and 
as defined in (4), the system (7) can be reduced to
(9)
According to (8), Equation (9) can be rewritten as
(10)
It is clear that the right-hand side of the above equation is the negative gradient direction of the following barrier function 
whose kernel logarithmic barrier function is
.
Therefore, the aforementioned equation can be rewritten as
Inspired by the work of [4,7,9], and by making a slight modification of the standard Newton direction, the new feasibility step used in this paper, is defined by the following different system:
(11)
where the kernel function of 
is given by
(12)
Since
, the third equation in the system (11) can be rewritten as
(13)
In the sequel, the feasibility step will be based on the Equation (13).
3. Some Technical Results
We recall some interesting results from Klerk [1]. In the sequel, we denote the iterates after a centrality step as
, 
,
.
Lemma 2 Let X, S satisfy the Slater’s regularity condition and
. If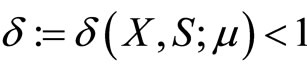
, then the fullNT step is strictly feasible.
Corollary 3 Let X, S satisfy the Slater’s regularity condition and
. If
. One has
.
Lemma 4 After a feasible full-NT step the proximity function satisfies
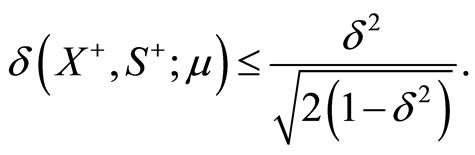
Lemma 5 If
, then
The required number of centrality steps can easily be computed. After the 
-update, one has 
, and hence after k centrality steps the iterates 
satisfy
From this, one deduces easily that 
holds, after at most
(14)
We give below a more formal description of the algorithm in Figure 1.
The following lemma stated without proof, will be useful for our analysis.
Lemma 6 (See [10], Lemma 2.5) For any
, one has
By applying Lemma (6), one can easily verify so that
for any
, we have:
(15)
and furthermore, according to (6), we obtain:
(16)
Lemma 7 According to the result of Corollary (3), for any 
one has
Proof. By applying Hölder inequality and using
, we obtain
and the result follows.
The following Lemma gives an upper bound for the proximity-measure of the matrix
.
Lemma 8 Let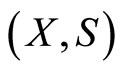 
be a primal-dual NT pair and 
such that
. Moreover let 
and
. Then
Proof. Since the 
is a primal-dual pair and by applying Lemma (7), and the two inequalities (15) and (16), we can get:
since the last term in the last equality is negative. This completes the proof of the Lemma.
Lemma 9 (See [1], Lemma 6.1). If one has 
, 
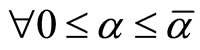, then
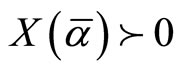, and
.
Let Q be an 
real symmetric matrix and M be an 
real skew-symmetric matrix, we recall the following result.
Lemma 10 (See [7], Lemma 3.8). If Q is positive definite, then
.
Lemma 11 (See [1], Lemma 6.3). If Q is positive definite, then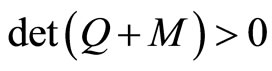
.
Lemma 12 (See [7], Lemma 3.10). Let A, 
, 
and
. Then
Lemma 13 (See [11], Lemma A.1) For
, let 
denote a convex functions. Then, for any nonzero
, the following inequality
holds.
4. Analysis of the Feasibility Step
4.1. The Feasibility Step
As established in Section 2, the feasibility step generates new iterates
, 
and 
that satisfy the Feasibility conditions for 
and 
(i.e., primal feasible and dual feasible), except possibly the positive semidefinite conditions. A crucial element in the analysis is to show that after the feasibility step, the inequality 
holds, i.e., that the new iterates are within the region where the Newton process targeting at the 
-centers of 
and 
is quadratically convergent. Let X, y and S denote the iterates at the start of an iteration and assume that
. Recall that at the start of the first iteration this is true since
. Defining 
and 
as in (4) and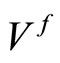 
as in (3). We may write
Therefore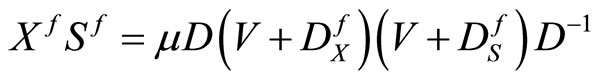 
which implies that
(17)
According to (8), Equation (13) can be rewritten as
(18)
and by multiplying both side from the left with V, we get
(19)
To simplify the notation in the sequel, we denote
(20)
Note that 
is symmetric and M is skew-symmetric. Now we may write, using (19),
By subtracting and adding
, to the last expression we obtain
Using (20) and (17), we get
(21)
Note that due to (8), 
is positive definite.
Lemma 14 Let 
and
. Then the iterates 
are strictly feasible if
.
Proof. We begin by introducing a step length
, and we define
We then have
, 
and similar relations for y and S. It is clear that
. We want to show that the determinant of 
remains positive for all
. We may write
By subtracting and adding 
and
to the right hand side of the above equality we obtain
where the matrix
is skew-symmetric for all
. Lemma (11) implies that the determinant of 
will be positive if the symmetric matrix
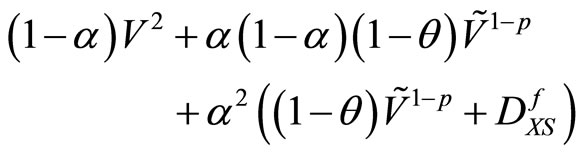
is positive definite which is true for all
. This means that 
has positive determinant. By positiveness of 
and 
and continuity of both 
and
, we deduce that 
and 
are positive definite which completes the proof.
We continue this section by recalling the following Lemma.
Lemma 15 (See [12], Lemma II. 60). Let 
be as given by (6) and
. Then
The proof of Lemma (15), together with
, makes clear that the elements of the vector 
satisfy
(22)
Furthermore, by using (8) and (22), we obtain the bounds of the elements of the vector 
(23)
In the sequel we denote
where
This implies
and
Lemma 16 Assuming
, one has
Proof. Using (6), we get
where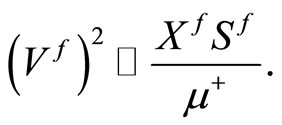 
From (21), one has
Due to the fact that 
since M is skewsymmetric and Lemma (10), we may write
where we apply for the third equality, Lemma (12) whose second condition is due to the requirement (24) given below.
For each
, we define
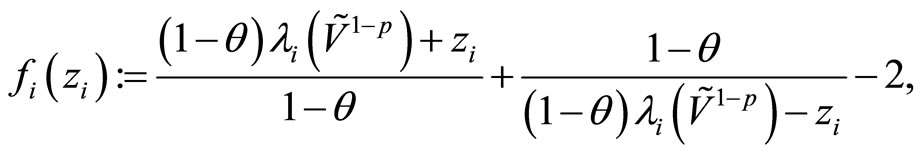
It is clear that 
is convex in 
if
. Taking
, we require
By applying Lemma (15), the above inequality holds if
(24)
By using Lemma (13), we may write
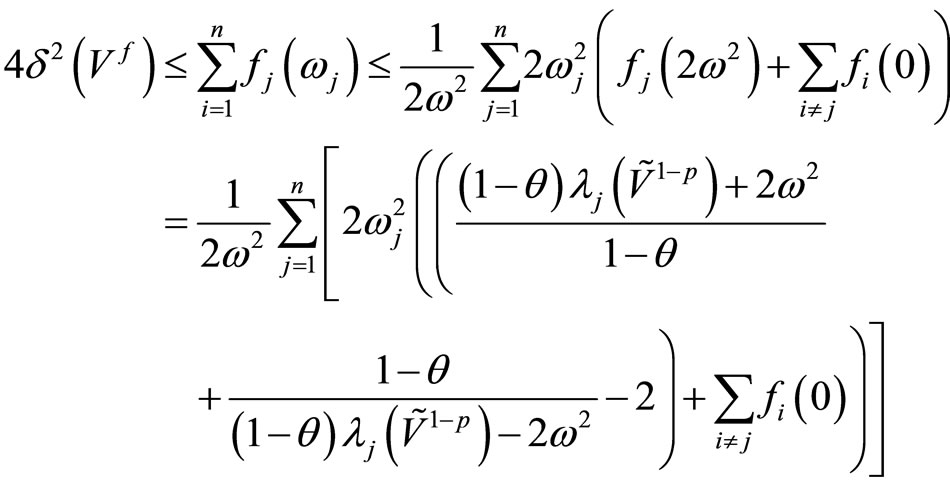
where
Furthermore, by using Lemma (8), we get
We deduce
where
Hence
The last equality is due to (24), which completes the proof.
Because we need to have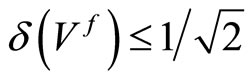
, it follows from this lemma that it suffices if
(25)
Now we decide to choose
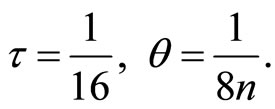(26)
Note that the left-hand side of (25) is monotonically increasing with respect to
. By some elementary calculations, for 
and
, we obtain
(27)
4.2. Upper Bound for 
In this section we consider the linear space
.
It is clear that the affine space
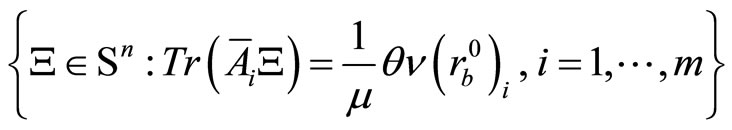
equals 
and
. We can get from Mansouri and Roos [6], the following result.
Lemma 17 (See [6], Lemma 5.11) Let Q be the (unique) matrix in the intersection of the affine spaces 
and
. Then
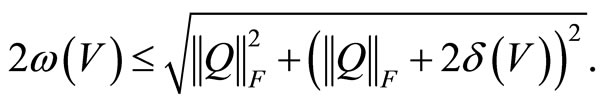
Note that (27) implies that we must have 
to guarantee
. Due to the above lemma, this will certainly hold if 
satisfies
(28)
Furthermore, according to Mansouri and Ross, we have
Since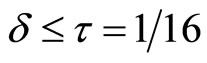
, we may write
By using
, the above inequality becomes
(29)
Because we are looking for the value that we do not allow 
to exceed and in order to guarantee that 
, (28) holds if 
satisfies
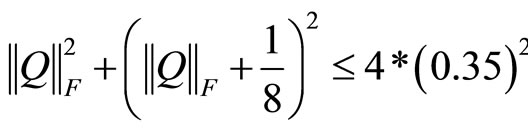, since
. This will be certainly satisfied if
. Hence, combining this with (29), we deduce that 
holds.
4.3. Iteration Bound
In the previous sections, we have found that, if at the start of an iteration the iterates satisfies
, with
, then after the feasibility step, with 
as defined in (26), the iterates satisfies
. According to (14), at most 
centering steps suffice to get iterates that satisfy
. So each main iteration consists of at most 3 so-called inner iterations. In each main iteration both the duality gap and the norms of the residual vectors are reduced by the factor
. Hence, using
, the total number of main iterations is bounded above by
Since
, the total number of inner iterations is so bounded above by
5. Concluding Remarks
In this paper we extended the full-Newton step infeasible interior-point algorithm to SDP. We used a specific kernel function to induce the feasibility step and we analyzed the algorithm based on this kernel function. The iteration bound coincides with the currently best known bound for IIPMs. Future research might focuses on studying new kernel functions.
6. Acknowledgements
The authors gratefully acknowledge the help of the guest editor and anonymous referees in improving the readability of the paper.