Projection Pursuit Dynamic Cluster Model and its Application to Water Resources Carrying Capacity Evaluation ()
1. Introduction
The difficulty frequently encountered in water resources carrying capacity evaluation is that there are so many factors and the complex interrelationship among them, which cannot be evaluated according to only one factor, all the effect factors associated with water resources carrying capacity must be thought over. However, up till now, there is no a unified standard of evaluation index system in the world. Presently, it is difficult to resolve complex high dimensional problem directly. If there is an effective way to reduce the dimensionality, multidimensional space problems can be resolved on visual space, such as three-dimensional space, two-dimensional space even one-dimensional space.
Friedman and Tukey developed a projection pursuit principle [1]. It is able to find a right projection direction that can retain the main feature of data according to a projection index. On the basis of the right projection direction, high dimensional problem can be converted to low dimensional problem such as one-dimension. Therefore, high dimensional data characteristics can be analyzed on two-dimensional or one-dimensional space, and many ordinary methods used on low dimensional space can be used to analyze high dimensional problems.
According to projection pursuit principle, many new mathematical analysis methods for high-dimensional data exploratory analysis also have been developed [2-8], and projection pursuit cluster (PPC) model is one of them. The PPC model is an effective method for multifactor data exploratory analysis, which is widely used in multivariable prediction, cluster and evaluation [9-15].
However, the PPC model does have disadvantage in practice as follows: 1) Being the only parameter in the PPC model, the cutoff radius is hard to estimate, even though it has a significant effect on the results. Nowadays, the cutoff radius are still set based on experience, i.e. it may be set to ten percent of the square root of the data variance along the largest principal axis [1]. There is no theory or common formula to calibrate the cutoff radius. 2) The cluster results cannot directly be obtained from the output of the PPC model. The PPC model only can provide the projected characteristic value remaining the major characteristics of data according to the projection index. In other words, other approaches such as the method of scatter points should be used to re-analyze the projected characteristic value series in order to obtain the desired cluster results [16].
In order to resolve the problem mentioned above, Wang and Ni developed a projection pursuit dynamic cluster (PPDC) model and it was used in regional partition of water resources in China [16]. In this paper, the PPDC model will be used in water resources carrying capacity evaluation in China for the first time. The PPDC model and its application will be introduced in detail in the following.
2. PPDC Model
A linear projection technique is described in this study. High-dimensional data is projected onto one-dimensional space, and the feature of high-dimensional data was studied through the projected characteristics of the one-dimensional space [1].
If 
(
and
. 
is the total number of samples, 
is the total number of effect factors of sample) is the initial value of the 
factor of the 
sample, the steps of developing the PPDC model are the following [16].
2.1. Data Standardization
In order to eliminate the effect of different ranges of values of cluster factors, the initial data are standardized before it is used in the PPDC model. And the standardization formula used in this study is
(1)
where 
and 
are the initial maximum and minimum of the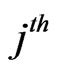 
factor respectively.
2.2. Linear Projection
In essence, projection is to observe data characteristic from all angles. The main purpose of projection pursuit is to find hidden structure in higher-dimensional data sets by searching through all their low-dimensional projections [17]. If 
is a 
-dimensional unit vector and 
is the projected characteristic value of
, linear projection can be described as,
(2)
where 
is projection axis vector, and it is also called projection direction vector in the PPC model.
2.3. Projection Index
Cluster analysis is a tool for exploratory data analysis that tries to find the intrinsic structure of data by organizing patterns into groups or clusters [18]. In the PPDC model, a new projection index is generated on the basis of dynamic cluster principle [19].
Define 
(
) as the absolute value of distance between the projected characteristic values 
and
, namely
.
Let
, and define 
as
(3)
Then, assume that the all samples are classified as 
(
) clusters. 
is the projected characteristic value space of cluster
, which contains all the projected characteristic values of cluster
, and that
(4)
where
, and
, 
and 
is the initial cluster core of both cluster 
and cluster
, respectively. In practice, the average projected characteristic value of clusters is used as new cluster core to conduct the iteration until the criterion is met [19].
Next define
(5)
and
(6)
Finally, according to 
and
, the new projection index 
in the PPDC model can be defined as
(7)
The bigger the value of 
is, the bigger of distance between data points will be, and the smaller the value of 
is, the smaller of distance between data points will be. The projection index measures the degree to which the data points in the projection are both concentrated locally (
small) while, at the same time, expanded globally (
large) [1].
2.4. Model Optimization
According to the above analysis, the PPDC model can be expressed by
(8)
From (8), it is shown that the PPDC model reflects an optimum problem. Genetic algorithm (GA) has been able to converge with global optimum while coping with the large and complex problems [20]; it possesses powerful and efficient search ability in the complex search space [21]. And it has been widely used in practice recently [10-12,22-25]. Here, the GA is used to resolve the optimization problem of the PPDC model, and the steps are introduced in detail in [16].
3. Case Study
The PPDC model is used in water resources carrying capacity evaluation in China. Five major factors of water resources carrying capacity are selected as index system: 1) per capita available amount of water resources (m3·person-1), 2) per unit GDP available amount of water resources (10-2 m3·(RMB Yuan)-1), 3) available amount of water resources per the estimated price of 45 kinds of potential resources (10-2 m3·(RMB Yuan )-1), 4) per arable area available amount of water resources(m3·hm-2) and 5) per unit area of available amount of water resources (104 m3·km-2). This Index system may reflect the water resources supporting capacity for population development (1 factor), economy development (2 and 3 factors) and eco-environment protection (4 and 5 factors). The data is shown in Table 1 [26].
The IPPC model is used to do a cluster analysis of regional partition in China according to its water resources carrying capacity.
In order to comparative analysis, we do water resources carrying capacity clustering in two cases, namely three clusters and four clusters. Based on the data in Table 1, we can develop the PPDC model. Here m = 5, n = 30 and p = 3 or 4.
The right projection direction 
is, when p = 3
and when 
.
The projected characteristic value z and the cluster results also can be got, which are shown in Table 1, too.
In Table 1, cluster 1 means the best situation of water resources carrying capacity in this administrative area, cluster 2 means better, and by analogy to others.
The schematic diagram of regional partition of water resources carrying capacity in China is shown in Figure 1.
The bigger the value of z is, the better the water resources carrying capacity will be. According to the index system in this study, the results of the PPDC model led
(a)
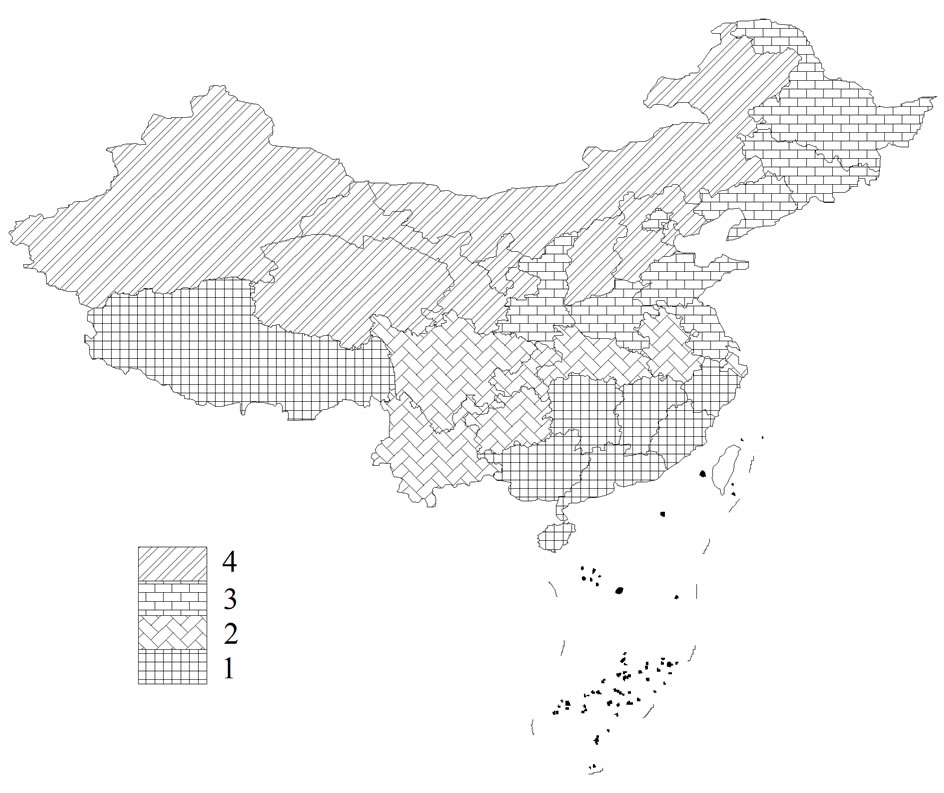(b)
Figure 1. Schematic diagram of regional partition of water resources carrying capacity in China: (a) three clusters; (b) four clusters.
to four major conclusions: 1) the situation of water resources carrying capacity in south China is better than that of in north China. Tibet Autonomous Region, Guangdong Province and Fujian Province are the first three regions being the best in water resources carrying capacity in China. That is to say, in the regions of cluster 1, the development of society and economy may be very suitable for water resources situation; 2) the most regions being poor level of water resources carrying capacity are centered largely in north China and Gansu Panhandle. Ningxia Hui Autonomous Region is a serious situation of water resources carrying capacity, and Inner Mongolia Autonomous Region, Gansu Province and Xinjiang Uygur Autonomous Region next; 3) the cluster results in this study are consistent with the facts of China. Because many rivers such as Yangtze River, Ya-lu-tsang-pu River, Nujiang-Salween River, Lancangjiang-Mekong River, and Pearl River run through or rise in the southern part of China, there are abundant water resources in south China. There is good water resources carrying capacity in south China, too. Therefore, South-to-North Water Transfer Project that is being put into practice is one of the effective measures to improve the water resources carrying capacity level for north China; 4) the distribution situation of regional partition of water resources carrying capacity is similar to that of water resources quantity in China [16].
4. Conclusions
The PPDC model combines dynamic cluster method with projection pursuit principle, which is an effective improvement for the PPC model. Because there is no parameter calibration and the final result of need can be outputted directly, the PPDC model is easy to operate in practice. The studies show that the PPDC model is a new method for water resources carrying capacity evaluation. However, the application of the PPDC model in multifactor evaluation needs to be improved further. On the other hand, water quality is one of the main factors of water resources carrying capacity, which related to the availability of water resource. Because of lacking water quality data, there are no water quality indexes in evaluation index system in this research. The evaluation in this study is mainly focus on the water resources quantity rather than water quality.
5. Acknowledgements
This work is part of the Program of China Meteorological Administration (CCFS-09-19) and Institute of Plateau Meteorology of China Meteorological Administration (BROP200801 and BROP200907). The constructive comments and suggestions from the editor and anonymous reviewers, which resulted in a significant improvement of the manuscript, are gratefully appreciated. The opinions expressed here are those of the authors and not those of other individuals or organizations.