1. Introduction
Cactus graph is a connected graph in which every block is a cycle or an edge, in other words, no edge belongs to more than one cycle. Cactus graphs have been extensively studied and used as models for many real-world problems. This graph is one of the most useful discrete mathematical structures for modelling problems arising in the real-world. It has many applications in various fields, like computer scheduling, radio communication system, etc. Cactus graphs have been studied from both theoretical and algorithmic points of view. This graph is a subclass of planar graph and superclass of tree.
An  -labelling of a graph
-labelling of a graph  is a function of
is a function of  from its vertex set
from its vertex set  to the set of nonnegative integers such that
to the set of nonnegative integers such that  if
if  and
and  if
if , where
, where  is the distance between the vertices
is the distance between the vertices  and
and , i.e., the number of edges between
, i.e., the number of edges between  and
and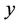 . The span of an
. The span of an  -labelling
-labelling  of
of  is max
is max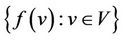 . The
. The  -labelling
-labelling  of
of  is the smallest
is the smallest  such that
such that  has a
has a  - labelling of span
- labelling of span .
.
An interesting graph-labelling problem comes from the radio frequency assignment problem, as well as code assignment in computer networks. One version of the radio channel assignment problem [1] is to assign integer channels to a network of transmitters with distance restrictions, such that the several labels of interference between nearby transmitters are avoided and the span of the label used is minimized. A variation of the problem is code assignment in computer networks, i.e., to assign integer control codes to a network of computer stations with distance restrictions.
Bertossi and Bonuccelli [2] introduced a kind of code assignment to avoid hidden terminal interference; this is as follows. Since some modern computer networks consist of including mobile computers or computer displaced in wide areas, they need to use broadcast communication media such as busses (only in local area networks) or radio frequencies. The computer network which communicates by radio frequencies is called Packet Radio Network. It consists of computer stations (computers and transceivers), in which the transceivers broadcast outgoing message packets and listen for incoming message packets. Unconstrained transmission in broadcast media may lead to collision on interference, i.e., there is the time-overlap of two or more incoming message packets received at the destination station. This results in damaged useless packets at the destination. Collided message packets must be retransmitted. That increases the time delay of the transmission, and hence lowers the system throughput. Several protocols have been devised to reduce or eliminate the collisions. They form the medium access control sublayer. For example, under Code Division Multiple Access protocol, the collision-free property is guaranteed by the use of proper assignment of orthogonal control codes to stations and the spread of spectrum communication techniques (e.g., hopping over different time slots or frequency bands).
We represent the network by a graph, such that all stations are vertices and two vertices are adjacent if the corresponding stations can hear each other. Hence, two stations are at distance two, if they are outside the hearing range of each other but can be received by the same destination station. There are two types of collisions-interferences: direct collision, due to transmission of adjacent station, and hidden terminal collision, when stations at distance two transmit to the same receiving station at the same time.
To avoid hidden terminal interference, we assign a control codes to each station in the software as follows. For one station, to avoid hidden terminal interference from its adjacent stations (which hear each other) sending packets to it, we require distinct codes for its immediate adjacent station, i.e., . Here we suppose that there is a little direct interference in the system, i.e., direct interference is so week that we can ignore it. Apparently in the model of [2] there are some special hardware designs, which can avoid direct interference in the system. Hence, we allow the same code for two adjacent stations (which can hear each other), meaning
. Here we suppose that there is a little direct interference in the system, i.e., direct interference is so week that we can ignore it. Apparently in the model of [2] there are some special hardware designs, which can avoid direct interference in the system. Hence, we allow the same code for two adjacent stations (which can hear each other), meaning . Therefore, we have the
. Therefore, we have the  -labelling case.
-labelling case.
It is important to note that the  -labelling problem is just a special case of ordinary graph labelling. Each feasible
-labelling problem is just a special case of ordinary graph labelling. Each feasible  -labelling of a graph
-labelling of a graph  yields a feasible labelling of the graph
yields a feasible labelling of the graph , where
, where  contains edge
contains edge 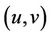 whenever
whenever 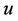 and
and  are distance two apart in
are distance two apart in . Conversely, a labelling of
. Conversely, a labelling of  becomes a feasible labelling of
becomes a feasible labelling of 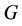 by calling the labels
by calling the labels , where
, where  represents the maximum colour number of the graph.
represents the maximum colour number of the graph.
In this paper, we label the vertices of a cactus graph 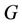 by
by  -labelling and it is shown that
-labelling and it is shown that 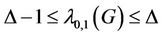 , where
, where  is the degree of the graph
is the degree of the graph , i.e.,
, i.e.,  max{deg(vi):
max{deg(vi): , deg(vi)) is the degree of the vertex vi)}.
, deg(vi)) is the degree of the vertex vi)}.
2. Review of Previous Works
Some results are available on  -labelling problem. Here we discuss some particular cases. When
-labelling problem. Here we discuss some particular cases. When  and
and  then we get
then we get 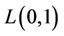 -labelling problem. Several results are known for
-labelling problem. Several results are known for  -labelling of graphs, but, to the best of our knowledge no result is known for cactus graph. In this section, the known result for general graphs and some related graphs of cactus graph are presented.
-labelling of graphs, but, to the best of our knowledge no result is known for cactus graph. In this section, the known result for general graphs and some related graphs of cactus graph are presented.
The upper bound for  of any graph
of any graph  is
is  [3], where
[3], where  is the degree of the graph.
is the degree of the graph.
The problem is simple for paths  of
of  vertices. It can easily be verified that
vertices. It can easily be verified that ,
,  for
for 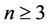 [4].
[4].
When the first and the last vertices of  are merged then
are merged then  becomes
becomes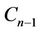 . In [2], Bertossi and Bonuccelli showed that
. In [2], Bertossi and Bonuccelli showed that  is equal to 1 if n is multiple of 4 and 2 otherwise.
is equal to 1 if n is multiple of 4 and 2 otherwise.
For complete graph , it is easy to check that
, it is easy to check that .
.
The wheel , is obtained by joining
, is obtained by joining  and
and , i.e.,
, i.e., . It is also easy to check that
. It is also easy to check that  .
.
Bertossi and Bonuccelli [2] investigated the  - labelling problem on complete binary trees, proving that 3 labels suffice. An optimum labelling as follows can be found. Assign first labels 0, 1 and 2, respectively, to the root, its left child and its right child. Then, consider the nodes by increasing levels: if a node has been assigned label
- labelling problem on complete binary trees, proving that 3 labels suffice. An optimum labelling as follows can be found. Assign first labels 0, 1 and 2, respectively, to the root, its left child and its right child. Then, consider the nodes by increasing levels: if a node has been assigned label , then assign the remaining labels to its grandchildren, but giving different to brother grandchildren. The above procedure can be generalized to find an optimum
, then assign the remaining labels to its grandchildren, but giving different to brother grandchildren. The above procedure can be generalized to find an optimum  -labelling for complete (
-labelling for complete (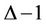 )-ary trees, requiring span
)-ary trees, requiring span . It is straight forward to see that when
. It is straight forward to see that when  and
and  this result gives the
this result gives the  - number for complete binary trees and paths respectively.
- number for complete binary trees and paths respectively.
It is shown in [5] that for any tree ,
,  is equal to
is equal to , implying that
, implying that . An optimal
. An optimal  -labelling can be also determined by exploiting the algorithm provided in [6] for optimally
-labelling can be also determined by exploiting the algorithm provided in [6] for optimally  - labelling trees.
- labelling trees.
Bodlaender et al. [7] compute upper bounds for graphs of treewidth bounded by  proving that
proving that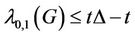 . They give also approximation algorithms for the
. They give also approximation algorithms for the 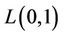 - labelling running in
- labelling running in  time.
time.
In [2], the NP-completeness result for the decision version of the  -labelling problem is derived when the graph is planar by means of a reduction from 3-VERTEX COLORING of straight-line planar graph. An exhausted survey on
-labelling problem is derived when the graph is planar by means of a reduction from 3-VERTEX COLORING of straight-line planar graph. An exhausted survey on 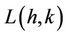 -labelling is available in [8].
-labelling is available in [8].
In [7], an approximation algorithm is designed for  -labelling a permutation graph in
-labelling a permutation graph in 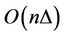 time; it guarantees the bound
time; it guarantees the bound .
.
The n-dimensional hypercube  is an
is an  -regular graph with
-regular graph with 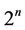 nodes. Then
nodes. Then  and there exists a labelling scheme using such a number of labels. This labelling is optimal when
and there exists a labelling scheme using such a number of labels. This labelling is optimal when  for some
for some  and it is a 2-approximation otherwise [9]. For a bipartite graph,
and it is a 2-approximation otherwise [9]. For a bipartite graph,  [7]. Later this lower bound has been improved by a constant factor of
[7]. Later this lower bound has been improved by a constant factor of 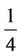 [10]. A study on
[10]. A study on 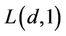 -labelling of cartesian product of a cycle and path is done by Chiang and Yan [11].
-labelling of cartesian product of a cycle and path is done by Chiang and Yan [11].
When  and
and  then we get
then we get  -labelling problem. This problem was introduced by Grrigs and Yeh [12,13] in connection with the problem of assigning frequencies in a multihop radio network. Some results of
-labelling problem. This problem was introduced by Grrigs and Yeh [12,13] in connection with the problem of assigning frequencies in a multihop radio network. Some results of 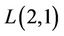 -labelling problem are given below.
-labelling problem are given below.
Kral and Skrekovski [14] improve the upper bound for any graph ,
,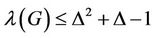 . The best known result till date is
. The best known result till date is  due to Goncalves [15].
due to Goncalves [15].
Heuvel and Mc Guinness showed that  [16] for planar graphs. Molloy and Salavatipour [17] reduced this upper bound to
[16] for planar graphs. Molloy and Salavatipour [17] reduced this upper bound to . Wang and Lih [18] proved that if
. Wang and Lih [18] proved that if  is a planar graph of girth (girth is defined to be the length of a shortest cycle in
is a planar graph of girth (girth is defined to be the length of a shortest cycle in ) at least 5, then
) at least 5, then 
In [19], we have showed that the upper and the lower bounds for  of a cactus graph
of a cactus graph  is
is 
Adams et al. [20], give different bounds for certain generalized petersen graphs. A study on  -labelling of cartesian product of a cycle and a path is done by Chiang and Yan [11].
-labelling of cartesian product of a cycle and a path is done by Chiang and Yan [11].
For further studies on the  -labelling, see [21- 30].
-labelling, see [21- 30].
When  and
and  then we get another special case which is called
then we get another special case which is called  -labelling problem. Some results of
-labelling problem. Some results of  -labelling problem are given below.
-labelling problem are given below.
For path,  and
and  for each
for each , and
, and  is 2 if
is 2 if  is a multiple of 3 and it is 3 otherwise [31].
is a multiple of 3 and it is 3 otherwise [31].
3. The L(0,1)-Labelling of Induce Sub-Graphs of Cactus Graphs
Let  be a given graph and subset
be a given graph and subset  of
of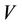 . The induced subgraph by
. The induced subgraph by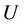 , denoted by
, denoted by  is the graph given by
is the graph given by , where
, where  . Some induced subgraphs of cactus graph are shown in Figure 1.
. Some induced subgraphs of cactus graph are shown in Figure 1.
The cactus graphs have many interesting subgraphs, those are illustrated below. An edge is nothing but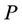 ,
,
 (a) (b) (c) (d)
(a) (b) (c) (d)
Figure 1. Some induce subgraphs of cactus graph.
so . The star graph
. The star graph 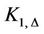 is a subgraph of cactus graph, therefore, one can conclude the following result.
is a subgraph of cactus graph, therefore, one can conclude the following result.
Lemma 1. For any star graph 
 (1)
(1)
4. L(0,1)-Labelling of Cycles
In [2], Bertossi and Bonuccelli have labeled 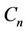 by
by  -labelling and they have obtained the following result. Here we have given a constructive prove of this result.
-labelling and they have obtained the following result. Here we have given a constructive prove of this result.
4.1. L(0,1)-Labelling of One Cycle
Lemma 2. [2] For any cycle 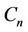 of length
of length ,
,
 (2)
(2)
Proof. Let  be the vertices of the cycle
be the vertices of the cycle . We classify
. We classify 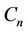 into five groups, viz.,
into five groups, viz.,  ,
,  ,
,  ,
,  and
and .Then the
.Then the  -labelling of the vertices of a cycle are as follows.
-labelling of the vertices of a cycle are as follows.
Case 1. Let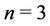 .
.

Case 2. Let  (mod 4), i.e.,
(mod 4), i.e., .
.

Case 3. Let  (mod 4), i.e.,
(mod 4), i.e., .
.
The label of first  vertices
vertices  are same as in Case 2. For the last vertex
are same as in Case 2. For the last vertex ,
,  is define as
is define as
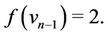
Case 4. Let  (mod 4), i.e.,
(mod 4), i.e., .
.
Here the label of first 4k + 1 vertices  are same as in Case 3. For the last vertex
are same as in Case 3. For the last vertex ,
,  is define as
is define as

Case 5. Let 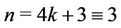 (mod 4), i.e.,
(mod 4), i.e.,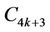 .
.
The label of first  vertices
vertices  are same as in Case 2. For the last three vertices
are same as in Case 2. For the last three vertices ,
,  ,
,  ,
,  is define as
is define as
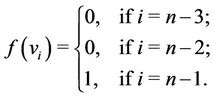
Thus, from all above cases, we conclude that

4.2. L(0,1)-Labelling of Two Cycles
Lemma 3. Let G be a graph which contains two cycles and they have a common cutvertex. If  be the degree of G, then
be the degree of G, then
 (3)
(3)
Proof. Let  contains two cycles
contains two cycles  and
and  of lengths
of lengths  and
and  respectively. Let
respectively. Let 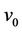 be the cutverx and
be the cutverx and  be the degree of
be the degree of . Let
. Let  and
and  be the vertices of
be the vertices of 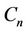 and
and  respecvely. The labelling procedure of
respecvely. The labelling procedure of ’s of
’s of  of same as given in Lemma 2. Now we label the cycle
of same as given in Lemma 2. Now we label the cycle 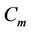 as follows.
as follows.
Case 1. Let  and
and .
.
The label of the cutvertex  is 0, i.e.,
is 0, i.e., . The label of other vertices of
. The label of other vertices of  are as follows:
are as follows:

Case 2. For  (mod 4) and
(mod 4) and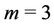 .
.
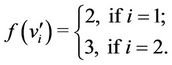
Case 3. For  (mod 4) and
(mod 4) and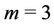 .
.

Case 4. For 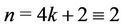 (mod 4) and
(mod 4) and .
.
The label of the vertices of  are same as given in Case 3 of that lemma.
are same as given in Case 3 of that lemma.
Case 5. For  (mod 4) and
(mod 4) and 
In this case, we label the of 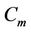 as given in Case 3.
as given in Case 3.
Case 6. For  (mod 4) and
(mod 4) and .
.
Here we label the adjacent vertices of 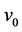 by
by  and
and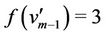 . Now we label the other vertices
. Now we label the other vertices  of
of  as follows.
as follows.

The above  is redefine for the vertex
is redefine for the vertex 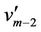 as
as
 .
.
In particular when , then we label the vertices of
, then we label the vertices of  as follows.
as follows.
The label of the cutvertex  and two adjacent vertices
and two adjacent vertices  and
and 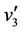 are same as above. And we label the remaining vertex
are same as above. And we label the remaining vertex 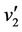 by
by .
.
Case 7. For 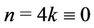 (mod 4) and
(mod 4) and  (mod 4).
(mod 4).
Here the label of two vertices ,
,  of
of 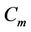 are same as given in the above case. Now we label the vertices
are same as given in the above case. Now we label the vertices 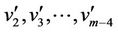 as
as

For the vertices  and
and ,
,  is defined as
is defined as  and
and 
In particular when , then we label the vertices of
, then we label the vertices of 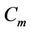 as follows.
as follows.
The label of the cutvertex  and two adjacent vertices of
and two adjacent vertices of 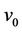 of
of  are same as above. Now we label the remaining vertices of
are same as above. Now we label the remaining vertices of  as
as

Case 8. For  (mod 4) and
(mod 4) and  (mod 4).
(mod 4).
The label of  of
of  are same as in above case. For the vertex
are same as in above case. For the vertex , we label it as
, we label it as
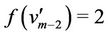 .
.
When , then the label of the vertices
, then the label of the vertices ,
,  ,
,  ,
,  and
and  are same as in the above case, and
are same as in the above case, and .
.
Case 9. For  (mod 4) and
(mod 4) and  (mod 4).
(mod 4).
We label the vertices of  and the vertices
and the vertices ,
,  ,
,  ,
, 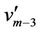 and
and  of
of  according to the Case 8. For the vertex
according to the Case 8. For the vertex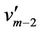 ,
, 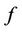 is
is

In particular, when , the the label of the vertices of
, the the label of the vertices of  are same as the label of the vertices of
are same as the label of the vertices of  as in the above case except the vertex
as in the above case except the vertex . The label of the vertex
. The label of the vertex  is
is 
Case 10. For  (mod 4) and
(mod 4) and  (mod 4).
(mod 4).
We label first  vertices
vertices  of
of  as
as

For the last four vertices ,
,  ,
, 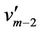 and
and , the above
, the above  is define as
is define as

In particular when , the label of the vertices
, the label of the vertices ,
,  ,
,  and
and  are same as the label of the vertices
are same as the label of the vertices  shown above.
shown above.
Case 11. For  (mod 4) and
(mod 4) and  (mod 4).
(mod 4).
We label first  vertices
vertices  of
of  as per Case 10. And for the last five vertices,
as per Case 10. And for the last five vertices,  is define as
is define as

In particular when  then the label of the vertices
then the label of the vertices 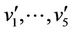 are same as the label of the last five vertices of
are same as the label of the last five vertices of 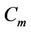 of the above case.
of the above case.
Case 12. For  (mod 4) and
(mod 4) and  (mod 4).
(mod 4).
Now we label first 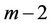 vertices of
vertices of  as
as

For the last two vertices  and
and , the
, the  is
is

Case 13. For  (mod 4) and
(mod 4) and  (mod 4).
(mod 4).
Here we label the other vertices of 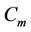 as in Case 11.
as in Case 11.
Case 14. For  (mod 4) and
(mod 4) and  (mod 4).
(mod 4).
In this case, the label of  are same as in Case 12.
are same as in Case 12.
Case 15. For  (mod 4) and
(mod 4) and  (mod 4).
(mod 4).
We label the vertices of  as per Case 12.
as per Case 12.
Thus from the above cases, it follow that
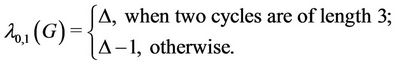
4.3. L(0,1)-Labelling of Three Cycles
Lemma 4. Let G be a graph, contains three cycles and they have a common cutvertex . If
. If  be the degree of
be the degree of , then,
, then,
 (4)
(4)
Proof. Let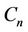 ,
, 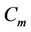 and
and 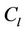 be three cycles join by a common cutvertex
be three cycles join by a common cutvertex , of lengths
, of lengths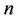 ,
,  and
and  respectively. Let
respectively. Let  be the degree of the cutvertex, i.e.,
be the degree of the cutvertex, i.e., . Let
. Let ,
,  ,
,  ,
, ;
;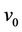 ,
,  ,
,  ,
,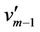 ;
; ,
,  ,
,  ,
,  be the vertices of the cycles respectively.
be the vertices of the cycles respectively.
Now we label the graph as follows.
Case 1. Let ,
,  and
and .
.
In Case 1 of Lemma 3, we label a graph which contains two cycles of length three and they have a common cutvertex . According to the previous lemma we label the vertices of the third cycle of length 3 as follows:
. According to the previous lemma we label the vertices of the third cycle of length 3 as follows:

Case 2. For ,
, 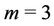 ,
,  , where
, where  .
.
All the subcases of this case, the label of two vertices  and
and  of the cycle
of the cycle  are
are
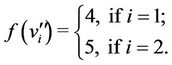
and the label of other two cycles are of different types, they are discussed below.
When  (mod 4) and
(mod 4) and .
.
Here the label of the vertices of the cycles  and
and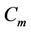 , joined with a common cutvertex
, joined with a common cutvertex  are same as in Case 2 of Lemma 3.
are same as in Case 2 of Lemma 3.
When  (mod 4) and
(mod 4) and .
.
The label of the vertices of  and
and 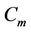 are same as in Case 3 of Lemma 3.
are same as in Case 3 of Lemma 3.
When  (mod 4) and
(mod 4) and .
.
The label of the vertices of  and
and  are same as in Case 4 of Lemma 3.
are same as in Case 4 of Lemma 3.
When  (mod 4) and
(mod 4) and .
.
We label the vertices of  and
and  as in Case 5 of Lemma 3.
as in Case 5 of Lemma 3.
Case 3. For ,
,  ,
, 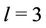 , where
, where  .
.
In all subcases of this case, the label of three vertices of 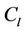 are
are

And the label of the vertices of first two cycles  and
and  are same as in Case 6, Case 7, ..., Case 15, respectively of Lemma 3.
are same as in Case 6, Case 7, ..., Case 15, respectively of Lemma 3.
Case 4. For ,
,  ,
,  (mod 4), where
(mod 4), where .
.
For all subcases of this case, we label the vertices of the third cycle  as same as the labelling of the vertices of
as same as the labelling of the vertices of  in Case 6 of Lemma 3 except two vertices
in Case 6 of Lemma 3 except two vertices  and
and  (the adjacent vertices of
(the adjacent vertices of ). Then we label these vertices as
). Then we label these vertices as 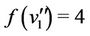 and
and .
.
And we label the first two cycles  and
and  (joined by a common cutvertex
(joined by a common cutvertex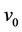 ), as same as in Case 6, Case 7, ..., Case 15 of Lemma 3.
), as same as in Case 6, Case 7, ..., Case 15 of Lemma 3.
Case 5. For ,
,  ,
, 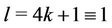 (mod 4), where
(mod 4), where .
.
In all subcases of this case, we label the vertices of the third cycle  using the same process to labelling the vertices of
using the same process to labelling the vertices of 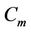 in Case 7 of Lemma 3 except two vertices
in Case 7 of Lemma 3 except two vertices  and
and  (the adjacent vertices of
(the adjacent vertices of ). Now we label the adjacent vertices of
). Now we label the adjacent vertices of  of
of  as
as  and
and .
.
And we label the first two cycles 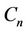 and
and 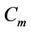 (joined by a common cutvertex
(joined by a common cutvertex ), as same as in Case 10, Case 11, ..., Case 15 of Lemma 3.
), as same as in Case 10, Case 11, ..., Case 15 of Lemma 3.
Case 6. For ,
,  ,
,  (mod 4), where
(mod 4), where .
.
In all subcases of this case, we label the vertices of the third cycle 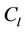 using the same process of labelling of the vertices of
using the same process of labelling of the vertices of  in Case 7 of Lemma 3, except two vertices
in Case 7 of Lemma 3, except two vertices  and
and . The label of
. The label of  and
and  are
are 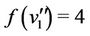 and
and .
.
And the label of the vertices of the cycles  and
and  are same as in Case 13, Case 14 and Case 15 respectively of Lemma 3.
are same as in Case 13, Case 14 and Case 15 respectively of Lemma 3.
Case 7. For  (mod 4),
(mod 4),  (mod 4),
(mod 4), 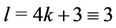 (mod 4).
(mod 4).
The label of the vertices of  and
and 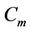 are same as in Case 15 of Lemma 3. Here
are same as in Case 15 of Lemma 3. Here . Then we label the vertices of
. Then we label the vertices of  using the same process of
using the same process of  in Case 9 of Lemma 3 except the vertices
in Case 9 of Lemma 3 except the vertices  and
and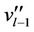 . We label these vertices as
. We label these vertices as  and
and . Thus from all above cases, it follow that
. Thus from all above cases, it follow that

4.4. L(0,1)-Labelling of Four Cycles
Using th results from Lemma 3 and Lemma 4 we can write the following statement.
Lemma 5. Let G be a graph which contains four cycles of any length and they have a common cutvertex. Then,
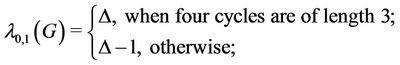 (5)
(5)
where  be the degree of the cutvertex.
be the degree of the cutvertex.
Corollary 1. Let G be a graph which contains finite number of cycles and they have a common cutvertex. If the vertices of the cycles (except the cutvertex) contain one or more edges then,
 (6)
(6)
4.5. L(0,1)-Labelling of Finite Number of Cycles
Let  be a graph which contains
be a graph which contains 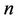 number of cycles of length 3. Sometimes a cycle of length three is called triangle. A triangle is a subgraph of a cactus graph. Also, a triangle shaped star, (i.e., all the triangles that have a common cutvertex) is a subgraph of a cactus graph. Now, we consider a triangle shaped star for
number of cycles of length 3. Sometimes a cycle of length three is called triangle. A triangle is a subgraph of a cactus graph. Also, a triangle shaped star, (i.e., all the triangles that have a common cutvertex) is a subgraph of a cactus graph. Now, we consider a triangle shaped star for 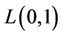 -labelling. Let
-labelling. Let 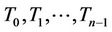 be the
be the  triangles meet at a common cutvertex
triangles meet at a common cutvertex 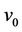 and we denote this graph by
and we denote this graph by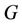 which is equivalent to
which is equivalent to . The number of vertices and edges of
. The number of vertices and edges of  are
are  and
and  respectively. Again the graph
respectively. Again the graph  may also contains
may also contains  number of cycles of finite length.
number of cycles of finite length.
Then from Lemmas 3-5 we conclude the general form of these lemmas which is given below.
Lemma 6. Let the graph G contains n number of cycles of any length and they joined at a cutvertex, then
 (7)
(7)
where 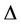 be the degree of the cutvertex.
be the degree of the cutvertex.
Proof. At first we prove that when  contains
contains  number of cycles of length 3 then the value of
number of cycles of length 3 then the value of  is
is , where
, where  be the degree of the graph. Let
be the degree of the graph. Let  be the
be the 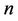 number of triangles joined with a common cutvertex
number of triangles joined with a common cutvertex  (shown in Figure 2).
(shown in Figure 2).
Let ,
, 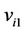 and
and  be the vertices of
be the vertices of , where
, where . We label
. We label  by 0.
by 0.
Then according to the previous lemmas the labels of

Figure 2. A graph contains n numbers of triangles.
 ’s are as follows.
’s are as follows.
For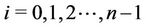 ,
,

Now, the label of the vertex  of
of  is
is  .
.
Therefore,  , when
, when 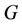 contains
contains  number of cycles of length 3.
number of cycles of length 3.
Again, if we consider a graph  contains
contains 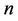 number of
number of  and
and  number of
number of , then,
, then, 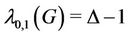 , where
, where  be the degree of cutvertex, then the general form can be proved by mathematical induction, that is, when a graph
be the degree of cutvertex, then the general form can be proved by mathematical induction, that is, when a graph 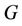 contains finite number of cycles of any length then
contains finite number of cycles of any length then .
.
Let  contains
contains 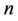 number of
number of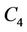 ’s
’s 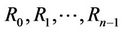 and
and  number of
number of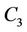 ’s
’s . Let
. Let 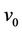 be the common vertex and degree of
be the common vertex and degree of  is
is . Again let
. Again let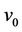 ,
,  ,
,  ,
,  be the vertices of
be the vertices of  and
and ,
, 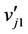 ,
, 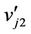 be the vertices of
be the vertices of . We label
. We label  as 0. Then we label the other vertices of
as 0. Then we label the other vertices of ’s as follows.
’s as follows.
For 

and then the label of the vertices of ’s are given by.
’s are given by.
For j = 0, 1, ···, n − 1,
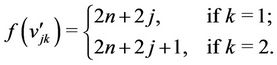
Now the label of third vertex of  is
is
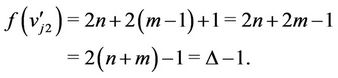
Therefore,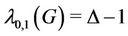 .
.
The general form can be proved by mathematical induction.
Hence the result.
Lemma 7. If a graph G contains finite number of cycles of any length and finite number of edges and they have a common cutvertex of degree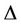 , then
, then
 (8)
(8)
Proof. Suppose that the lemma is true for  number of cycles of any length and
number of cycles of any length and  number of edges. Now we have to prove that if we add a cycle of any length to the cutvertex then the value of
number of edges. Now we have to prove that if we add a cycle of any length to the cutvertex then the value of  for the new graph will be same, i.e., the value of
for the new graph will be same, i.e., the value of  will preserve for
will preserve for  number of cycles of any length.
number of cycles of any length.
Now the graph  contains
contains  number of cycles of any length and
number of cycles of any length and  number of edges joined with a common cutvertex
number of edges joined with a common cutvertex . Then the degree of
. Then the degree of  is
is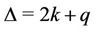 . In the previous lemma we proved that when a graph contains finite number of cycles of any length then,
. In the previous lemma we proved that when a graph contains finite number of cycles of any length then,

At first we prove that if 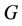 contains
contains  number of cycles of length 3 and
number of cycles of length 3 and 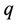 number of edges then the value of
number of edges then the value of 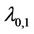 for that graph remains same. When all cycles are of length 3 then according to the Lemma 5 the label of two vertices of
for that graph remains same. When all cycles are of length 3 then according to the Lemma 5 the label of two vertices of 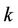 th cycle of length 3 are as
th cycle of length 3 are as

where ,
,  and
and  are three vertices of
are three vertices of  th cycle. Let
th cycle. Let ,
, ;
; ,
, ;
; ;
; ,
,  are the vertices of
are the vertices of  edges. Here the label of the cutvertex
edges. Here the label of the cutvertex 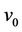 is 0. Then we label the other vertices of the edges as follows
is 0. Then we label the other vertices of the edges as follows

Now we add another cycle of length 3 to the cutvertex . Then the degree of
. Then the degree of  is
is . Let
. Let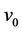 ,
, 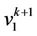 and
and  be the vertices of
be the vertices of  th cycle. We label the two vertices
th cycle. We label the two vertices 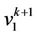 and
and  as
as

Here we see that the label of third vertex of  th cycle is
th cycle is  as
as . That is, the value of
. That is, the value of 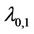 of the graph which contains
of the graph which contains  number of cycles of length 3 and
number of cycles of length 3 and  number of edges is same.
number of edges is same.
Similarly, we can prove that the value of  will preserve for the graph which contains
will preserve for the graph which contains  number of cycles and
number of cycles and  number of edges.
number of edges.
Hence the result.
5. L(0,1)-Labelling of Sun
Let us consider the sun  of
of  vertices. This graph is obtained by adding an edge to each vertex of a cycle
vertices. This graph is obtained by adding an edge to each vertex of a cycle . So
. So  is a subgraph of
is a subgraph of . But, what is the value of
. But, what is the value of 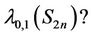
Lemma 8. For any sun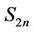 ,
,
 (9)
(9)
Proof. Let  be constructed from
be constructed from  by adding an edge to each vertex. To label this graph we consider five cases.
by adding an edge to each vertex. To label this graph we consider five cases.
Let  be the vertices of
be the vertices of  and
and  is adjacent to
is adjacent to  and
and . To complete
. To complete , we add an edge (
, we add an edge ( ,
, ) to the vertex
) to the vertex , i.e.,
, i.e.,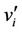 ’s are the pendent vertices. The labelling procedure of
’s are the pendent vertices. The labelling procedure of  is same as given in Lemma 2. Now we label the pendent vertices as follows.
is same as given in Lemma 2. Now we label the pendent vertices as follows.
Case 1. Let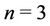 .
.
The label of  's are as
's are as

Case 2. Let  (mod 4).
(mod 4).
The label of  are assigned as
are assigned as  for
for .
.
Case 3. Let  (mod 4).
(mod 4).
The label of the vertices ’s are given by
’s are given by
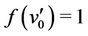 ;
;  for
for  and
and  and
and .
.
Case 4. Let  (mod 4).
(mod 4).
The label of the vertices 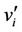 's are given by
's are given by
 , for
, for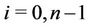 ;
;
 for
for ;
;
 , for
, for .
.
Case 5. Let 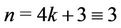 (mod 4).
(mod 4).
In this case the label of the pendent vertices 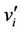 's are as follows:
's are as follows:
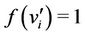 , for
, for ;
;
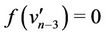 ;
; , for
, for .
.
Hence .
.
Lemma 9. Let  be a graph obtained from
be a graph obtained from  by adding an edge to each of the pendent vertex of
by adding an edge to each of the pendent vertex of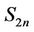 , then
, then
 (10)
(10)
Proof. Let the graph is obtained by adding an edge  to each of the pendent vertices
to each of the pendent vertices  s. So in the new graph
s. So in the new graph  are the pendent vertices.
are the pendent vertices.
Case 1. Let .
.
 ,
,  , for
, for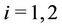 .
.
Case 2. Let 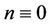 (mod 4).
(mod 4).
 , for
, for .
.
Case 3. Let  (mod 4).
(mod 4).
 ,
,  and
and , for
, for  .
.
Case 4. Let  (mod 4).
(mod 4).

and , for
, for .
.
Case 5. Let  (mod 4).
(mod 4).
 , for
, for , and
, and , for
, for .
.
Thus, from all above cases we have
 .
.
Lemma 10. If the graph  contains a cycle of any length and each vertex of the cycle has another cycle of any length, then
contains a cycle of any length and each vertex of the cycle has another cycle of any length, then
 (11)
(11)
where  is the degree of
is the degree of .
.
Proof. At first we prove that if the graph 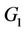 contains a cycle
contains a cycle  of length
of length  and each vertex of
and each vertex of  contains another cycle of length 3, or length 3 and length 4, or length 4, then
contains another cycle of length 3, or length 3 and length 4, or length 4, then  or
or . Let
. Let  be the vertices of
be the vertices of  and
and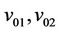 ;
; ;
; ;
;  are the vertices of all
are the vertices of all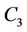 ’s which are joined with each vertex of
’s which are joined with each vertex of . If the vertex
. If the vertex  of
of  contains a cycle of length 4 then let the vertices of
contains a cycle of length 4 then let the vertices of 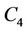 be
be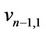 ,
,  and
and . Again if the vertex
. Again if the vertex  contains a cycle of length 4 then let the vertices of
contains a cycle of length 4 then let the vertices of  be
be ,
,  and
and . Therefore, all the vertices of
. Therefore, all the vertices of  are cutvertices.
are cutvertices.
Now we label the graph as follows.
Case 1. For .
.
Now, we label the vertices of other cycles joined with the vertices of  according to the following rule
according to the following rule

If there are three cycles of length 4 then we label the vertices as follows:

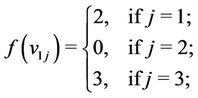
and 
Case 2. Let  (mod 4).
(mod 4).
For ,
,

If all other cycles are of length 4 then the label of the last vertex of the last cycle is 3.
Case 3. Let  (mod 4).
(mod 4).


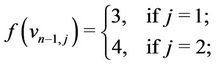
and 
If the ( )th vertex
)th vertex 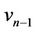 of
of  contains a cycle of length 4 then we label the vertices of
contains a cycle of length 4 then we label the vertices of  as
as
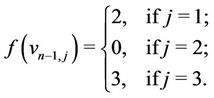
Case 4. Let  (mod 4).
(mod 4).
Now the label of all  's are as follows:
's are as follows:
for ,
, 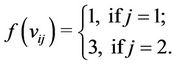
for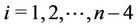 ,
, 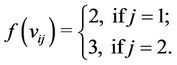
and for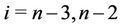 ,
, 
If  contain combined
contain combined  's and
's and  's then the minimum span is 3.
's then the minimum span is 3.
Case 5. Let  (mod 4).
(mod 4).
For ,
, 

and for ,
, 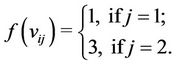
If the vertex  contains a cycle of length 4 then the label of the vertices adjacent to
contains a cycle of length 4 then the label of the vertices adjacent to  are
are

From all the above cases, we see that 3 or 4 are used to label , which is equal to
, which is equal to  or
or .
.
Therefore, .
.
The proves of the other cases are similar.
Corollary 2. Let G be a graph which contains a cycle of length . If each vertex of the cycle contains two or more cycles of length more than 2, then
. If each vertex of the cycle contains two or more cycles of length more than 2, then
 (12)
(12)
where  be the degree of G.
be the degree of G.
6. L(0,1)-Labelling of Caterpillar Graph
Now, we label another important subclass of cactus graphs called caterpillar graph.
Definition 1. A caterpillar 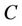 is a tree where all vertices of degree
is a tree where all vertices of degree  lie on a path, called the backbone of
lie on a path, called the backbone of . The hairlength of a caterpillar graph
. The hairlength of a caterpillar graph  is the maximum distance of a non-backbone vertex to the backbone.
is the maximum distance of a non-backbone vertex to the backbone.
Lemma 11. If G be a caterpillar graph and  be its degree, then
be its degree, then
 (13)
(13)
Proof. Let  be a path of length
be a path of length  of the caterpillar graph and
of the caterpillar graph and  be the vertices of
be the vertices of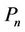 . We label the vertices of
. We label the vertices of  according to the following rule.
according to the following rule.

Let us assume that 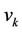 be any vertex of
be any vertex of  and
and ,
,  are the adjacent vertices of
are the adjacent vertices of . As we label of the vertices of
. As we label of the vertices of  by 0 or 1 so without loss of generality let us consider that the label of
by 0 or 1 so without loss of generality let us consider that the label of ,
, 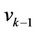 and
and  are 0, 0 and 1 respectively. Again let us consider that
are 0, 0 and 1 respectively. Again let us consider that  number of paths
number of paths ;
; , of same lengths are joined to the vertex
, of same lengths are joined to the vertex . Let
. Let ;
; 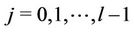
 are the vertices of
are the vertices of  paths other than
paths other than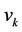 . Now we label the vertices of these paths as in the following method:
. Now we label the vertices of these paths as in the following method:
 for
for  and
and .
.
And we label other vertices of  's as per the rule to label the vertices of
's as per the rule to label the vertices of .
.
Now, .
.
The result will be same when finite number of paths of different lengths are joined to one or more vertices of the path of the caterpillar graph.
So, .
.
7. L(0,1)-Labelling of Lobster
Another subclass of cactus graphs is the lobster graph. The definition of lobster graph is given below.
Definition 2. A lobster is a tree having a path (of maximum length) from which every vertex has distance at most , where
, where 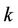 is an integer.
is an integer.
The maximum distance of the vertex from the path is called the diameter of the lobster graph. There are many types of lobsters given in literature like diameter 2, diameter 4, diameter 5, etc.
Lemma 12. Let G be a lobster graph. If 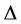 be the degree of the lobster graph, then
be the degree of the lobster graph, then
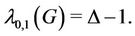 (14)
(14)
Proof. Let  be a path of length
be a path of length  of the lobster graph and
of the lobster graph and  be the vertices of
be the vertices of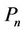 . First we label the vertices of
. First we label the vertices of  according to Lemma 11.
according to Lemma 11.
Then we label the other vertices of that graph. Let us denote the other vertices of the graph by . Here
. Here  are adjacent to
are adjacent to  and
and ,
, . The label of the vertices of
. The label of the vertices of  are either 0 or 1. Then we label the vertices
are either 0 or 1. Then we label the vertices  by 2, 3 and so on [it depends upon (
by 2, 3 and so on [it depends upon (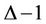 )].
)].
Thus the  -value of a lobster is
-value of a lobster is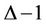 .
.
We know from [2] that 3 labels are sufficent to label a complete binary tree by  -labelling. Now we have to prove that for any tree the value of
-labelling. Now we have to prove that for any tree the value of  is
is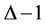 , where
, where  is the degree of the tree.
is the degree of the tree.
Lemma 13. For any tree  of degree
of degree ,
,
 (15)
(15)
Proof. Let 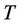 be a tree with degree
be a tree with degree . We first label the root of the tree by 0. Now we know from the definition of
. We first label the root of the tree by 0. Now we know from the definition of  -labelling that the label difference between any two adjacent vertices is at least 0 and the label difference between any two vertices which are at distance two is at least 1. Now we label the children of the root from left to right by 0, 1, 2,
-labelling that the label difference between any two adjacent vertices is at least 0 and the label difference between any two vertices which are at distance two is at least 1. Now we label the children of the root from left to right by 0, 1, 2,  ,
, .
.
Let us consider the  th vertex of the tree. Assume that the label of the parent of
th vertex of the tree. Assume that the label of the parent of  is known. Then the allowable label for the children of
is known. Then the allowable label for the children of  are 0, 1, 2,
are 0, 1, 2,  except the label of the parent of
except the label of the parent of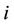 . Now, we label the children of
. Now, we label the children of  by 0, 1, 2,
by 0, 1, 2,  ,
,  ,
,  , where
, where 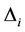 is the degree of the vertex
is the degree of the vertex , except the label of the parent of
, except the label of the parent of . This process is valid for any vertex
. This process is valid for any vertex 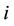 of the tree. Thus the maximum label used to label the entire tree by
of the tree. Thus the maximum label used to label the entire tree by  -labelling is max{
-labelling is max{ :
:  }, which is exactly equal to
}, which is exactly equal to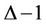 .
.
Hence .
.
The  -labelling of all subgraphs of cactus graphs and their combinations are discussed in the previous lemmas. From these results we conclude that the
-labelling of all subgraphs of cactus graphs and their combinations are discussed in the previous lemmas. From these results we conclude that the  -value of any cactus graph can not be more than
-value of any cactus graph can not be more than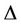 . Hence we have the following theorem.
. Hence we have the following theorem.
Theorem 1. If  is the degree of a cactus graph
is the degree of a cactus graph , then
, then
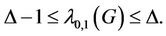 (16)
(16)
The graph of Figure 3 is an example of a cactus graph, contains all possible subgraphs and its 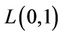 -labelling.
-labelling.
8. Conclusion
The bounds of  -labelling of a cactus graph and various subclass viz., cycle, sun, star, caterpillar, lobster and tree are investigated. The bounds of
-labelling of a cactus graph and various subclass viz., cycle, sun, star, caterpillar, lobster and tree are investigated. The bounds of  for these graphs are
for these graphs are 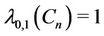 or 2, for sun, star, caterpillar, lobster and tree it is
or 2, for sun, star, caterpillar, lobster and tree it is . For the cactus graph the bound is
. For the cactus graph the bound is , where
, where  is the
is the

Figure 3. L(0,1)-labelling of a cactus graph.
maximum degree of the cactus graph . Currently we are engaged to find the bounds for
. Currently we are engaged to find the bounds for  -labelling for different values of
-labelling for different values of ,
,  on cactus graphs.
on cactus graphs.