Tribonacci Cordial Labeling of Graphs

Sarbari Mitra, Soumya Bhoumik

Department of Mathematics, Fort Hays State University, Hays, USA.

DOI: 10.4236/jamp.2022.104098                

Abstract

We introduce Tribonacci cordial labeling as an extension of Fibonacci cordial labeling, a well-known form of vertex-labelings. A graph that admits Tribonacci cordial labeling is called Tribonacci cordial graph. In this paper we investigate whether some well-known graphs are Tribonacci cordial.

Keywords

Tribonacci Cordial, Generalized Friendship Graph, Wheel Graph, Ring Sum, Joint Sum

1. Introduction

Throughout the paper we assume that G is a simple connected graph of order n.

Definition 1.1 A function $f\mathrm{<mo>\; :\; </mo>}V\mathrm{<mo\; stretchy="false">\; (\; </mo>}G\mathrm{<mo\; stretchy="false">\; )\; </mo>}\to \mathrm{<mo>\; \{\; </mo>0,1\; <mo>\; \}\; </mo>}$ is said to be Cordial Labeling if the induced function $f^{\mathrm{<mo>\; *\; </mo>}}\mathrm{<mo>\; :\; </mo>}E\mathrm{<mo\; stretchy="false">\; (\; </mo>}G\mathrm{<mo\; stretchy="false">\; )\; </mo>}\to \mathrm{<mo>\; \{\; </mo>0,1\; <mo>\; \}\; </mo>}$ defined by

$f^{*}(uv)=|f(u)-f(v)|$

satisfies the conditions $\mathrm{<mo>\; |\; </mo>}{v}_f\mathrm{<mo\; stretchy="false">\; (\; </mo>0\; <mo\; stretchy="false">\; )\; </mo>}-v_f\mathrm{<mo\; stretchy="false">\; (\; </mo>1\; <mo\; stretchy="false">\; )\; </mo>\; <mo>\; |\; </mo>}\le 1$ , as well as $\mathrm{<mo>\; |\; </mo>}{e}_f\mathrm{<mo\; stretchy="false">\; (\; </mo>0\; <mo\; stretchy="false">\; )\; </mo>}-e_f\mathrm{<mo\; stretchy="false">\; (\; </mo>1\; <mo\; stretchy="false">\; )\; </mo>\; <mo>\; |\; </mo>}\le 1$ , where

$v_f\mathrm{<mo\; stretchy="false">\; (\; </mo>0\; <mo\; stretchy="false">\; )\; </mo>}$ : = number of vertices with label 0,

$v_f\mathrm{<mo\; stretchy="false">\; (\; </mo>1\; <mo\; stretchy="false">\; )\; </mo>}$ : = number of vertices with label 1,

$e_f\mathrm{<mo\; stretchy="false">\; (\; </mo>0\; <mo\; stretchy="false">\; )\; </mo>}$ : = number of edges with label 0,

$e_f\mathrm{<mo\; stretchy="false">\; (\; </mo>1\; <mo\; stretchy="false">\; )\; </mo>}$ : = number of edges with label 1.

The concept of cordial labeling was introduced by Cahit [1] through a variety of vertex labeling. This was further extended to various labeling such as divisor cordial labeling, product cordial labeling, total product cordial labeling, prime cordial labeling etc. (see [2] for a dynamic survey). Rokad and Ghodasara introduced Fibonacci cordial labeling [3] and provided a list of families of graphs that are Fibonacci cordial. Later this labeling was explored for several other families of graph (see [4] [5]). Motivated by their work, we investigate Tribonacci cordial labeling, which is an extension of the Fibonacci cordial labeling.

Definition 1.2 The sequence $T_n$ of Tribonacci numbers is defined by the third order linear recurrence relation (for $n\ge 0$ ):

$T_{n+3}=T_n+T_{n+1}+T_{n+2};T_0=0,T_1=T_2=1,$

Definition 1.3 An injective function $f\mathrm{<mo>\; :\; </mo>}V\mathrm{<mo\; stretchy="false">\; (\; </mo>}G\mathrm{<mo\; stretchy="false">\; )\; </mo>}\to \mathrm{<mo>\; \{\; </mo>}{T}_0\mathrm{,}{T}_1\mathrm{,}\cdots \mathrm{,}{T}_n\mathrm{<mo>\; \}\; </mo>}$ is said to be Tribonacci cordial labeling if the induced function $f^{\mathrm{<mo>\; *\; </mo>}}\mathrm{<mo>\; :\; </mo>}E\mathrm{<mo\; stretchy="false">\; (\; </mo>}G\mathrm{<mo\; stretchy="false">\; )\; </mo>}\to \mathrm{<mo>\; \{\; </mo>0,1\; <mo>\; \}\; </mo>}$ defined by

$f^{*}(uv)=(f(u)+f(v))(\mathrm{mod}2)$

satisfies the condition $\mathrm{<mo>\; |\; </mo>}{e}_f\mathrm{<mo\; stretchy="false">\; (\; </mo>0\; <mo\; stretchy="false">\; )\; </mo>}-e_f\mathrm{<mo\; stretchy="false">\; (\; </mo>1\; <mo\; stretchy="false">\; )\; </mo>\; <mo>\; |\; </mo>}\le 1$ . A graph which admits Tribonacci cordial labeling is called Tribonacci cordial graph.

In this paper we denote the total number of odd edges by $e\mathrm{<mo\; stretchy="false">\; (\; </mo>1\; <mo\; stretchy="false">\; )\; </mo>}$ (analogously $e\mathrm{<mo\; stretchy="false">\; (\; </mo>0\; <mo\; stretchy="false">\; )\; </mo>}$ for even edges) and $e\mathrm{<mo\; stretchy="false">\; (\; </mo>1\; <mo\; stretchy="false">\; )\; </mo>}-e\mathrm{<mo\; stretchy="false">\; (\; </mo>0\; <mo\; stretchy="false">\; )\; </mo>}$ will be denoted as $\tilde{e}$ .

2. Main Results

In this section we examine whether some of the trivial graphs like $P_n$ , $C_n$ , $K_n$ are Tribonacci cordial. We can start with a simple observation that for any n, the sequence $\mathrm{<mo>\; \{\; </mo>}{T}_0\mathrm{,}{T}_1\mathrm{,}\cdots ,T_n\mathrm{<mo>\; \}\; </mo>}$ has m many evens, where

$m=(\begin{array}{ll}k+\mathrm{1,}\hfill & \text{if}n=2k+1\hfill \\ 2k+\mathrm{1,}\hfill & \text{if}n=4k\text{or}4k+2\hfill \end{array}$

Theorem 2.1 $P_n$ is Tribonacci cordial.

Proof. Let $f\mathrm{<mo>\; :\; </mo>}V\mathrm{<mo\; stretchy="false">\; (\; </mo>}{P}_n\mathrm{<mo\; stretchy="false">\; )\; </mo>}\to \mathrm{<mo>\; \{\; </mo>}{T}_0\mathrm{,}{T}_1\mathrm{,}\cdots T_n\mathrm{<mo>\; \}\; </mo>}$ be a labeling such that $f(v_i)=T_i$ for all $i=1,2,\cdots ,n$ . Clearly it implies that the value of ${\tilde{e}}_{P_n}$ is 0 if n is even and 1 otherwise.

Theorem 2.2 For any two assigned Tribonacci labeling (injective) $f\mathrm{<mo>\; :\; </mo>}V\mathrm{<mo\; stretchy="false">\; (\; </mo>}{C}_n\mathrm{<mo\; stretchy="false">\; )\; </mo>}\to \mathrm{<mo>\; \{\; </mo>}{T}_0\mathrm{,}{T}_1\mathrm{,}\cdots \mathrm{,}{T}_n\mathrm{<mo>\; \}\; </mo>}$ and $g\mathrm{<mo>\; :\; </mo>}V\mathrm{<mo\; stretchy="false">\; (\; </mo>}{C}_n\mathrm{<mo\; stretchy="false">\; )\; </mo>}\to \mathrm{<mo>\; \{\; </mo>}{T}_0\mathrm{,}{T}_1\mathrm{,}\cdots \mathrm{,}{T}_n\mathrm{<mo>\; \}\; </mo>}$ , ${\tilde{e}}_f-{\tilde{e}}_g\equiv 0(\mathrm{mod}4)$ .

Proof. Without loss of generality, suppose that f and g are the same Tribonacci labeling except at $v_0\in V\mathrm{<mo\; stretchy="false">\; (\; </mo>}{C}_n\mathrm{<mo\; stretchy="false">\; )\; </mo>}$ , i.e. $f\mathrm{<mo\; stretchy="false">\; (\; </mo>}{v}_0\mathrm{<mo\; stretchy="false">\; )\; </mo>}\ne g\mathrm{<mo\; stretchy="false">\; (\; </mo>}{v}_0\mathrm{<mo\; stretchy="false">\; )\; </mo>}$ . Let us consider $e_f(0)=m$ and hence $e_f(1)=n-m$ . Also consider $v_L$ and $v_R$ are two adjacent vertices of $v_0$ .

If $f^{*}(v_L{v}_0)\equiv 1(\mathrm{mod}2)$ and $f^{*}(v_0{v}_R)\equiv 0(\mathrm{mod}2)$ (or vice versa), then it is clear that

${\tilde{e}}_f={\tilde{e}}_g$

Otherwise without loss of generality, we may assume that

$f^{*}(v_L{v}_0)=f^{*}(v_0{v}_R)\equiv 0(\mathrm{mod}2)$

In this case, clearly $e_g\mathrm{<mo\; stretchy="false">\; (\; </mo>0\; <mo\; stretchy="false">\; )\; </mo>}$ will be either m or $m-2$ . Respectively $e_g\mathrm{<mo\; stretchy="false">\; (\; </mo>1\; <mo\; stretchy="false">\; )\; </mo>}$ will be either $n-m$ or $n-m+2$ . Thus

${\tilde{e}}_g-{\tilde{e}}_f=|e_g(0)-e_g(1)|-|e_f(0)-e_f(1)|\equiv 0(\mathrm{mod}4)$

Corollary 2.3 For any injective function $f\mathrm{<mo>\; :\; </mo>}V\mathrm{<mo\; stretchy="false">\; (\; </mo>}G\mathrm{<mo\; stretchy="false">\; )\; </mo>}\to \mathrm{<mo>\; \{\; </mo>}{T}_0\mathrm{,}{T}_1\mathrm{,}\cdots \mathrm{,}{T}_{2m}\mathrm{<mo>\; \}\; </mo>}$ on cyclic graph $C_{2m}$ , if $\left|\tilde{e}\right|\equiv 2(\mathrm{mod}4)$ , then $C_{2m}$ is not Tribonacci cordial.

As it is clear from the above Corollary, if $n\equiv 2(\mathrm{mod}4)$ , $C_n$ is not Tribonacci cordial under f, then any other function $g\mathrm{<mo>\; :\; </mo>}V\mathrm{<mo\; stretchy="false">\; (\; </mo>}G\mathrm{<mo\; stretchy="false">\; )\; </mo>}\to \mathrm{<mo>\; \{\; </mo>}{T}_0\mathrm{,}{T}_1\mathrm{,}\cdots \mathrm{,}{T}_{2m}\mathrm{<mo>\; \}\; </mo>}$ will not be able to generate ${\tilde{e}}_g\equiv 0(\mathrm{mod}4)$ . For $n\cancel{\equiv }2(\mathrm{mod}4)$ , we can consider the labeling $f\mathrm{<mo>\; :\; </mo>}V\mathrm{<mo\; stretchy="false">\; (\; </mo>}{C}_n\mathrm{<mo\; stretchy="false">\; )\; </mo>}\to \mathrm{<mo>\; \{\; </mo>}{T}_0\mathrm{,}{T}_1\mathrm{,}\cdots ,T_n\mathrm{<mo>\; \}\; </mo>}$ such that $f(v_i)=T_i$ for all $i=1,2,\cdots ,n$ . Clearly it produces odd and even edges alternatively. Thus we have the following theorem.

Theorem 2.4 $C_n$ is Tribonacci cordial, except $n\equiv 2(\mathrm{mod}4)$ .

Lemma 2.5 $K_{2m+1}$ is Tribonacci cordial only for $m\le 1.$

Proof. First note that the vertex labeling can be chosen from $T_0\mathrm{,}{T}_1\mathrm{,}\cdots \mathrm{,}{T}_{2m+1}$ , out of which $m+1$ labels are even and thus $m+1$ are odd. Since we only need $2m+1$ many labelings, we drop either an odd or an even Tribonacci number from the list. Without loss of generality, we use all of the Tribonacci numbers except an even one. As there are $m+1$ many odd and m many even vertex labels, $e(1)=m(m+1)$ , and $e(0)=\left(\begin{array}{c}m+1\\ 2\end{array}\right)+\left(\begin{array}{c}m\\ 2\end{array}\right)$ . Hence in order to be Tribonacci cordial we must have

$\left|\tilde{e}\right|=|m(m+1)-\left(\begin{array}{c}m+1\\ 2\end{array}\right)-\left(\begin{array}{c}m\\ 2\end{array}\right)|\le 1$

It simplifies to $\mathrm{<mo>\; |\; </mo>}m\mathrm{<mo>\; |\; </mo>}\le 1$ , which is only possible for $m=0,1$ , and hence $n=1,3$ .

Next we divide the case, n is even, into two categories, namely $n=4m$ , and $4m+2$ to get the following two lemmas.

Lemma 2.6 $K_{4m}$ is Tribonacci cordial only for $m=1.$

Lemma 2.7 $K_{4m+2}$ is Tribonacci cordial only for $m\le 1.$

The next theorem follows immediately from the previous lemmas, which provide the complete list of all complete graphs that are Tribonacci cordial.

Theorem 2.8 The complete list of Tribonacci cordial Complete graphs are $K_1\mathrm{,}{K}_2\mathrm{,}{K}_3\mathrm{,}{K}_4$ , and $K_6$ .

A wheel graph $W_n$ is a graph that contains a cycle of n many vertices such that every vertex of the cycle is connected with another vertex known as the hub (see Figure 1).

Figure 1. Tribonacci cordial labeling for $W_{17}$ graph.

Theorem 2.9 $W_n$ is Tribonacci cordial.

Proof. We start by identifying the vertices of $W_n$ as $V(W_n)=\left\{v\right\}\cup \{v_1,v_2,\cdots ,v_n\}$ where $v_i$ ’s are the vertices of the cycle in a clockwise manner and v is the hub of the cycle. Now, for $n=4p+q$ , where $0\le q\le 3$ , we define

$p_1=(\begin{array}{ll}p\mathrm{,}\hfill & \text{if}q=3\hfill \\ p-\mathrm{1,}\hfill & \text{otherwise}\hfill \end{array}$

and $p_2=p_1+2$ . The following function assigns Tribonacci labeling to the vertices of the wheel graphs. For $1\le i\le 2p_1$

$f\mathrm{<mo\; stretchy="false">\; (\; </mo>}{v}_i\mathrm{<mo\; stretchy="false">\; )\; </mo>}=(\begin{array}{ll}{T}_{i-2}\mathrm{,}\hfill & \text{if}i\equiv 0\mathrm{<mo\; stretchy="false">\; (\; </mo>}\mathrm{mod}\mathrm{4\; <mo\; stretchy="false">\; )\; </mo>}\hfill \\ T_{i+2}\mathrm{,}\hfill & \text{if}i\equiv 1\mathrm{<mo\; stretchy="false">\; (\; </mo>}\mathrm{mod}\mathrm{4\; <mo\; stretchy="false">\; )\; </mo>}\hfill \\ T_{i-1}\mathrm{,}\hfill & \text{if}i\equiv 2\mathrm{<mo\; stretchy="false">\; (\; </mo>}\mathrm{mod}\mathrm{4\; <mo\; stretchy="false">\; )\; </mo>}\hfill \\ T_{i+1}\mathrm{,}\hfill & \text{if}i\equiv 3\mathrm{<mo\; stretchy="false">\; (\; </mo>}\mathrm{mod}\mathrm{4\; <mo\; stretchy="false">\; )\; </mo>}\hfill \end{array}$

For the vertices $2p_1<i\le n$ , define $f(v_i)=T_k$ where

$k=(\begin{array}{ll}n+\mathrm{<mo\; stretchy="false">\; (\; </mo>}i-3p\mathrm{<mo\; stretchy="false">\; )\; </mo>}-2\lceil \frac{3p-i-2}{2}\rceil +1-q\mathrm{,}\hfill & \text{for}2p_1+1\le i\le 2p_1+p_2\mathrm{,}\text{and}q=\mathrm{0,1,2,3}\hfill \\ i-2\lfloor \frac{n-i-q}{2}\rfloor -\mathrm{2,}\hfill & \text{for}2p_1+p_2<i\le n\mathrm{,}\text{and}q=\mathrm{0,1,2}\hfill \\ i-2\lfloor \frac{n-i-2}{2}\rfloor -\mathrm{2,}\hfill & \text{for}2p_1+p_2<i\le n\mathrm{,}\text{and}q=3\hfill \end{array}$

Easy calculation ensures the validity of the cordiality of the labeling.

A shell graph is defined as a cycle $C_n$ with $\mathrm{<mo\; stretchy="false">\; (\; </mo>}n-\mathrm{3\; <mo\; stretchy="false">\; )\; </mo>}$ chords sharing a common vertex, called the apex (see Figure 2). Shell graphs are denoted as $C_{\mathrm{<mo\; stretchy="false">\; (\; </mo>}n\mathrm{,}n-\mathrm{3\; <mo\; stretchy="false">\; )\; </mo>}}$ . The vertices of $C_{\mathrm{<mo\; stretchy="false">\; (\; </mo>}n\mathrm{,}n-\mathrm{3\; <mo\; stretchy="false">\; )\; </mo>}}$ are denoted by $\mathrm{<mo>\; \{\; </mo>}{v}_1\mathrm{,}{v}_2\mathrm{,}\cdots \mathrm{,}{v}_n\mathrm{<mo>\; \}\; </mo>}$ , $v_1$ as the apex.

Theorem 2.10 Shell graphs $C_{\mathrm{<mo\; stretchy="false">\; (\; </mo>}n\mathrm{,}n-\mathrm{3\; <mo\; stretchy="false">\; )\; </mo>}}$ are Tribonacci cordial.

Proof. Let us rewrite n as $4p+q$ , where $0\le q\le 3$ and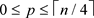. We define $p_1$ and $p_2$ as:

$p_1=(\begin{array}{ll}p\mathrm{,}\hfill & \text{if}q=\mathrm{0,1}\hfill \\ p+\mathrm{1,}\hfill & \text{if}q=\mathrm{2,3}\hfill \end{array}$

Figure 2. Tribonacci labeling for $C_{\mathrm{16,13}}$ graph.

and $p_2=2p+1-p_1$ . The function defined below assigns Tribonacci numbers to the vertices of the wheel graphs. Let $f(v_1)=T_1$ , and

$f\mathrm{<mo\; stretchy="false">\; (\; </mo>}{v}_i\mathrm{<mo\; stretchy="false">\; )\; </mo>}=(\begin{array}{ll}{T}_{i+1}\mathrm{,}\hfill & \text{if}i\equiv 0\mathrm{<mo\; stretchy="false">\; (\; </mo>}\mathrm{mod}\mathrm{4\; <mo\; stretchy="false">\; )\; </mo>}\hfill \\ T_{i-1}\mathrm{,}\hfill & \text{if}i\equiv 1\mathrm{<mo\; stretchy="false">\; (\; </mo>}\mathrm{mod}\mathrm{4\; <mo\; stretchy="false">\; )\; </mo>}\hfill \\ T_i\mathrm{,}\hfill & \text{otherwise}\hfill \end{array}$

for $2\le i\le 2p_1$ . For the vertices $2p_1<i\le n$ , let $f(v_i)=T_k$ where

$k=(\begin{array}{ll}n+(i-3p)-2\lceil \frac{3p-i-2}{2}\rceil -3-q,\hfill & \text{for}2p_1+1\le i\le 2p_1+p_2,\text{and}q=0,1,2,3\hfill \\ j-2\lfloor \frac{n-i-q}{2}\rfloor -2,\hfill & \text{for}2p_1+p_2<i\le n,\text{and}q=0,1,2\hfill \\ j-2\lfloor \frac{n-i-2}{2}\rfloor -2,\hfill & \text{for}2p_1+p_2<i\le n,\text{and}q=3\hfill \end{array}$

Easy calculation generates $e_1=n=e_0$ , which ensures that $W_n$ is Tribonacci cordial for all n.

The generalized friendship graph $F_{m\mathrm{,}n}$ (see Figure 3) is a collection of n many cycles $C_m$ , meeting at a common vertex. Clearly we can refer friendship graph $F_n$ as $F_{\mathrm{3,}n}$ . For convenience, let us call the common vertex v the apex, and each cycle a blade of the graph. Consider $V(F_{m,n})=\left\{v\right\}\cup {\{v_{i,1},v_{i,2},\cdots ,v_{i,m}\}}_{i=1}^n$ where the $i^{\text{th}}$ blade is $C_i=\{v{v}_{i,1}{v}_{i,2}\cdots v_{i,m},v\}$ . It is evident from the definition that the cardinality of the vertex and edge sets are given by $n\mathrm{<mo\; stretchy="false">\; (\; </mo>}m-\mathrm{1\; <mo\; stretchy="false">\; )\; </mo>}+1$ and $mn$ respectively.

Lemma 2.11 If $m\equiv 1(\mathrm{mod}2)$ and $n\equiv 2(\mathrm{mod}4)$ , then $F_{m\mathrm{,}n}$ is not Tribonacci cordial.

Proof. Note that in any blade, any combination of even and odd Tribonacci labeling on the vertices of the cycle $C_m$ including the apex vertex, generates only even values for $e_1$ . Thus $e_1\equiv 0(\mathrm{mod}2)$ . Now when $n=4k+2$ and $m=2p+1$ , for some integer $k\mathrm{,}p\ge 0$ , $|E(F_{m,n})|=8pk+4(p+k)+2$ . In order to generate Tribonacci cordial labeling for $F_{m\mathrm{,}n}$ , $e_1$ must be $4pk+\mathrm{2\; <mo\; stretchy="false">\; (\; </mo>}p+k\mathrm{<mo\; stretchy="false">\; )\; </mo>}+1$ , which clearly contradicts that $e_1$ is even.

Figure 3. Tribonacci cordial labeling for friendship graph $F_{\mathrm{5,4}}$ .

Now we investigate whether $F_{m\mathrm{,}n}$ is Tribonacci cordial for the remaining values, i.e., for $m\cancel{\equiv }0(\mathrm{mod}2)$ or $n\cancel{\equiv }2(\mathrm{mod}4)$ . First, we look into the case when $m\equiv 1(\mathrm{mod}2)$ and $n\cancel{\equiv }2(\mathrm{mod}4)$ to obtain the following.

Lemma 2.12 $F_{\mathrm{3,}n}$ is Tribonacci cordial if $n\cancel{\equiv }2(\mathrm{mod}4)$ .

Proof. For convenience, we redefine vertex $v_{ij}$ as $v_k$ , where $k=2(i-1)+j$ , and

$p=(\begin{array}{ll}n\mathrm{<mo>\; /\; </mo>2,}\hfill & \text{if}n\equiv 0\mathrm{<mo\; stretchy="false">\; (\; </mo>}\mathrm{mod}\mathrm{4\; <mo\; stretchy="false">\; )\; </mo>}\hfill \\ \mathrm{<mo\; stretchy="false">\; (\; </mo>}n+\mathrm{1\; <mo\; stretchy="false">\; )\; </mo>\; <mo>\; /\; </mo>2,}\hfill & \text{if}n\equiv 1\mathrm{<mo\; stretchy="false">\; (\; </mo>}\mathrm{mod}\mathrm{4\; <mo\; stretchy="false">\; )\; </mo>}\hfill \\ \mathrm{<mo\; stretchy="false">\; (\; </mo>}n-\mathrm{1\; <mo\; stretchy="false">\; )\; </mo>\; <mo>\; /\; </mo>2,}\hfill & \text{if}n\equiv 3\mathrm{<mo\; stretchy="false">\; (\; </mo>}\mathrm{mod}\mathrm{4\; <mo\; stretchy="false">\; )\; </mo>}\hfill \end{array}$

Now we provide the function that assigns Tribonacci numbers to the vertices of the $F_{\mathrm{3,}n}$ . For $n\equiv 0(\mathrm{mod}4)$ , we label v with $T_{2n+1}$ , and label the rest of the vertices as follow:

$f\mathrm{<mo\; stretchy="false">\; (\; </mo>}{v}_k\mathrm{<mo\; stretchy="false">\; )\; </mo>}=(\begin{array}{ll}{T}_{k+1}\mathrm{,}\hfill & \text{for}1\le k\le p\text{and}k\equiv 2\mathrm{<mo\; stretchy="false">\; (\; </mo>}\mathrm{mod}\mathrm{4\; <mo\; stretchy="false">\; )\; </mo>}\hfill \\ T_{k-1}\mathrm{,}\hfill & \text{for}1\le k\le p\text{and}k\equiv 3\mathrm{<mo\; stretchy="false">\; (\; </mo>}\mathrm{mod}\mathrm{4\; <mo\; stretchy="false">\; )\; </mo>}\hfill \\ T_k\mathrm{,}\hfill & \text{otherwise}\hfill \end{array}$

For $n\equiv 1,3(\mathrm{mod}4)$ ,

$f\mathrm{<mo\; stretchy="false">\; (\; </mo>}{v}_k\mathrm{<mo\; stretchy="false">\; )\; </mo>}=(\begin{array}{ll}{T}_{k-1}\mathrm{,}\hfill & \text{for}1\le k\le p\hfill \\ T_k\mathrm{,}\hfill & \text{for}p\le k\le 2n\hfill \end{array}$

and finally $f(v)=T_{n-1}$ .

Lemma 2.13 For $n\cancel{\equiv }2(\mathrm{mod}4)$ , $F_{\mathrm{5,}n}$ is Tribonacci cordial.

Proof. Let us define

$p=(\begin{array}{ll}3n\mathrm{<mo>\; /\; </mo>4,}\hfill & \text{if}n\equiv 0\mathrm{<mo\; stretchy="false">\; (\; </mo>}\mathrm{mod}\mathrm{4\; <mo\; stretchy="false">\; )\; </mo>}\hfill \\ \mathrm{<mo\; stretchy="false">\; (\; </mo>3}n+\mathrm{1\; <mo\; stretchy="false">\; )\; </mo>\; <mo>\; /\; </mo>4,}\hfill & \text{if}n\equiv 1\mathrm{<mo\; stretchy="false">\; (\; </mo>}\mathrm{mod}\mathrm{4\; <mo\; stretchy="false">\; )\; </mo>}\hfill \\ \mathrm{<mo\; stretchy="false">\; (\; </mo>3}n-\mathrm{1\; <mo\; stretchy="false">\; )\; </mo>\; <mo>\; /\; </mo>4,}\hfill & \text{if}n\equiv 3\mathrm{<mo\; stretchy="false">\; (\; </mo>}\mathrm{mod}\mathrm{4\; <mo\; stretchy="false">\; )\; </mo>}\hfill \end{array}$

The following function assigns Tribonacci labeling to the vertices of the graph $F_{\mathrm{5,}n}$ . For $1\le k\le p$ , $f(v_k)=T_k$ , and for $p+1\le k\le 4n$ we define

$f\mathrm{<mo\; stretchy="false">\; (\; </mo>}{v}_k\mathrm{<mo\; stretchy="false">\; )\; </mo>}=(\begin{array}{ll}{T}_{k+1}\mathrm{,}\hfill & \text{if}k\equiv 2\mathrm{<mo\; stretchy="false">\; (\; </mo>}\mathrm{mod}\mathrm{4\; <mo\; stretchy="false">\; )\; </mo>}\hfill \\ T_{k-1}\mathrm{,}\hfill & \text{if}k\equiv 3\mathrm{<mo\; stretchy="false">\; (\; </mo>}\mathrm{mod}\mathrm{4\; <mo\; stretchy="false">\; )\; </mo>}\hfill \\ T_k\mathrm{,}\hfill & \text{otherwise}\hfill \end{array}$

and finally $f(v)=T_{4n+1}$ . It can be easily observed that for each blade, excluding the common vertex v, we label two categories of labelings in the following order: viz. p many even-even-odd-odd, and $n-p$ many even-odd-even-odd. Hence the value of $\tilde{e}$ in each blade, of former kind is −1, and 3 on the later (as the common vertex is being labeled by an odd Tribonacci number). Consequently we obtain

$\tilde{e}=(\begin{array}{ll}\mathrm{0,}\hfill & \text{if}n\equiv 0\mathrm{<mo\; stretchy="false">\; (\; </mo>}\mathrm{mod}\mathrm{4\; <mo\; stretchy="false">\; )\; </mo>}\hfill \\ -\mathrm{1,}\hfill & \text{if}n\equiv 1\mathrm{<mo\; stretchy="false">\; (\; </mo>}\mathrm{mod}\mathrm{4\; <mo\; stretchy="false">\; )\; </mo>}\hfill \\ \mathrm{1,}\hfill & \text{if}n\equiv 3\mathrm{<mo\; stretchy="false">\; (\; </mo>}\mathrm{mod}\mathrm{4\; <mo\; stretchy="false">\; )\; </mo>}\hfill \end{array}$

We believe that the following holds

Conjecture 2.14 $F_{2k+\mathrm{1,}n}$ is Tribonacci cordial for $n\cancel{\equiv }2(\mathrm{mod}4)$ and any positive integer $k\ge 3$ .

Theorem 2.15 $F_{m\mathrm{,}n}$ is Tribonacci cordial if $m\equiv 2(\mathrm{mod}4)$ and $n\equiv 0(\mathrm{mod}2)$ or $m\equiv 0(\mathrm{mod}4)$ for any n.

Proof. Let $f\mathrm{<mo>\; :\; </mo>}V\mathrm{<mo\; stretchy="false">\; (\; </mo>}{F}_{m\mathrm{,}n}\mathrm{<mo\; stretchy="false">\; )\; </mo>}\to \mathrm{<mo>\; \{\; </mo>}{T}_0\mathrm{,}{T}_1\mathrm{,}\cdots \mathrm{,}{T}_{n\mathrm{<mo\; stretchy="false">\; (\; </mo>}m-\mathrm{1\; <mo\; stretchy="false">\; )\; </mo>}+1}\mathrm{<mo>\; \}\; </mo>}$ such that $f(v_i)=T_{(m-1)n+2-i}$ and $f(v)=T_1$ . It is clear for $m\equiv 0(\mathrm{mod}4)$ , each blade the vertices is getting the labels odd-even-even-odd- $\cdots$ -even-odd, which with the odd labeled common vertex result in $\tilde{e}=0$ . Thus we have a Tribonacci cordial graph for any choice of n.

Now for $m\equiv 2(\mathrm{mod}4)$ where $n\equiv 0(\mathrm{mod}2)$ , we can make the observation that the values of $\tilde{e}$ in each blade are to be $\mathrm{<mo>\; \{\; </mo>}-\mathrm{2,2,2,}-\mathrm{2,}-\mathrm{2,2,2,}-2,\cdots \mathrm{<mo>\; \}\; </mo>}$ . This clearly implies that that we have a Tribonacci cordial labeling ( $\tilde{e}=0$ ) when the number of blades are even, i.e., $n\equiv 0(\mathrm{mod}2)$ .

Theorem 2.16 $K_{m\mathrm{,}n}$ is Tribonacci cordial for all $m\mathrm{,}n$ .

Proof. Let us denote the vertices of $K_{m\mathrm{,}n}$ by $\mathrm{<mo>\; \{\; </mo>}{u}_1\mathrm{,}{u}_2\mathrm{,}\cdots \mathrm{,}{u}_m\mathrm{,}{v}_1\mathrm{,}{v}_2\mathrm{,}\cdots \mathrm{,}{v}_n\mathrm{<mo>\; \}\; </mo>}$ . In order to assign Tribonacci labeling to the graph $K_{m\mathrm{,}n}$ we consider the following cases.

Case 1. Assume that at least one of $m\mathrm{,}n$ is even. Without loss of generality we consider m to be even and use the following labeling: $f(u_i)=T_{i-1}$ , $f(v_i)=T_{m+i-1}$ . Note that, m/2 even and m/2 odd Tribonacci labels are used on one side, which result in $\tilde{e}=0$ , for any assignment of labels on the other side.

Case 2. Consider the case when both m and n are odd. Let $m=2k_1+1$ and $n=2k_2+1$ , following the same pattern of labeling as the previous case. It can be easily noted that there are either $k_1$ and $k_2+1$ , or $k_1+1$ and $k_2$ even labels used. The former case yields $\tilde{e}=k_1{k}_2+(k_1+1)(k_2+1)-k_1(k_2+1)-(k_1+1)k_2=1$ , whereas, later case implies $\tilde{e}=-1$ , ensuring the cordiality of the labeling in either one.

Bistar $B_{m\mathrm{,}n}$ is the graph obtained by joining the apex vertices of two copies of star, viz. $K_{\mathrm{1,}m}$ and $K_{\mathrm{1,}n}$ , by an edge. We identify the vertex set as $\mathrm{<mo>\; \{\; </mo>}{u}_i\mathrm{<mo>\; :\; </mo>1}\le i\le m\mathrm{<mo>\; \}\; </mo>}\cup \mathrm{<mo>\; \{\; </mo>}{v}_i\mathrm{<mo>\; :\; </mo>1}\le i\le n\mathrm{<mo>\; \}\; </mo>}\cup \mathrm{<mo>\; \{\; </mo>}u\mathrm{,}v\mathrm{<mo>\; \}\; </mo>}$ where $u\mathrm{,}v$ are the apex vertices and $u_i\mathrm{,}{v}_i$ are the pendant vertices connected with u and v respectively. The vertex and edge set cardinalities are given by $m+n+2$ and $m+n+1$ respectively.

Theorem 2.17 Bistar graph $B_{m\mathrm{,}n}$ are Tribonacci cordial.

Proof. Define the function $f\mathrm{<mo>\; :\; </mo>\; <mo\; stretchy="false">\; (\; </mo>}{B}_{m\mathrm{,}n}\mathrm{<mo\; stretchy="false">\; )\; </mo>}\to \mathrm{<mo>\; \{\; </mo>}{T}_0\mathrm{,}{T}_1\mathrm{,}\cdots \mathrm{,}{T}_{m+n+2}\mathrm{<mo>\; \}\; </mo>}$ as $f(u_i)=T_{i+1}$ , $f(v_i)=T_{m+i+1}$ which assigns Tribonacci numbers to all pendant vertices. In order to label the apex vertices $u\mathrm{,}v$ , consider the following cases.

Case 1. Let at least one of $m\mathrm{,}n$ is even. Without loss of generality we can assume that m is even. Label $f(u)=T_0$ and $f(v)=T_1$ if $m+n\equiv 1(\mathrm{mod}4)$ , and vice-versa if $m+n\cancel{\equiv }1(\mathrm{mod}4)$ . It is clear that m/2 many vertices are labeled with even (and odd) Tribonacci labels. Now if $m+n\equiv 1(\mathrm{mod}4)$ then $\mathrm{<mo\; stretchy="false">\; (\; </mo>}n-\mathrm{1\; <mo\; stretchy="false">\; )\; </mo>\; <mo>\; /\; </mo>2}$ many even and $\mathrm{<mo\; stretchy="false">\; (\; </mo>}n+\mathrm{1\; <mo\; stretchy="false">\; )\; </mo>\; <mo>\; /\; </mo>2}$ many odd Tribonacci labels are used on other side. Thus $\tilde{e}=m/2+1+(n-1)/2-m/2-(n+1)/2=0$ .

On the other hand if $m+n\cancel{\equiv }1(\mathrm{mod}4)$ , then there are 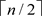many even and many odd Tribonacci labels used on the side of n pendant vertices. Hence.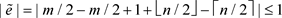

Case 2. Consider both $m\mathrm{,}n$ are odd. Once again without loss of generality we will consider three cases: $m\equiv 1(\mathrm{mod}4)$ and $n\equiv 1(\mathrm{mod}4)$ ; $m\equiv 3(\mathrm{mod}4)$ and $n\equiv 1(\mathrm{mod}4)$ ; $m\equiv 3(\mathrm{mod}4)$ and $n\equiv 3(\mathrm{mod}4)$ . For the first case $f(u)=T_1$ and $f(v)=T_0$ and vice-versa on last the two cases. It is very similar to the previous case to verify that this assigns a Tribonacci labeling to the graph $B_{m\mathrm{,}n}$ .

Theorem 2.18 Complete binary trees are Tribonacci cordial.

Proof. Let T be the complete binary tree. We denote the vertices as $\mathrm{<mo>\; \{\; </mo>}{v}_i^j\mathrm{<mo>\; :\; </mo>1}\le i\le 2^j\mathrm{,0}\le j\le \mathcal{l}\mathrm{<mo>\; \}\; </mo>}$ , where $\mathcal{l}$ denoted the levels, and $v_i^{\mathcal{l}}$ is connected to $v_{2i-1}^{\mathcal{l}+1}$ and $v_{2i}^{\mathcal{l}+1}$ . We define the labeling $f\mathrm{<mo>\; :\; </mo>}V\mathrm{<mo\; stretchy="false">\; (\; </mo>}T\mathrm{<mo\; stretchy="false">\; )\; </mo>}\to \mathrm{<mo>\; \{\; </mo>}{T}_0\mathrm{,}{T}_1\mathrm{,}\cdots \mathrm{,}{T}_{2n}\mathrm{<mo>\; \}\; </mo>}$ as $f(v_i^j)=T_{2^j+i-1}$ . If we denote $e_k$ as the edge connecting the vertices the parent and the child vertex $v_i^j$ , where $k=2^j+i-2$ , then we observe the following:

$f^{\mathrm{<mo>\; *\; </mo>}}\mathrm{<mo\; stretchy="false">\; (\; </mo>}{e}_k\mathrm{<mo\; stretchy="false">\; )\; </mo>}=(\begin{array}{cc}1\mathrm{<mo\; stretchy="false">\; (\; </mo>}\mathrm{mod}\mathrm{2\; <mo\; stretchy="false">\; )\; </mo>,}& \text{if}k\equiv \mathrm{1,4,6,7}\mathrm{<mo\; stretchy="false">\; (\; </mo>}\mathrm{mod}\mathrm{8\; <mo\; stretchy="false">\; )\; </mo>}\\ 0\mathrm{<mo\; stretchy="false">\; (\; </mo>}\mathrm{mod}\mathrm{2\; <mo\; stretchy="false">\; )\; </mo>,}& \text{if}k\equiv \mathrm{0,2,3,5}\mathrm{<mo\; stretchy="false">\; (\; </mo>}\mathrm{mod}\mathrm{8\; <mo\; stretchy="false">\; )\; </mo>}\end{array}$

As the maximum possible value for k is ${\mathrm{2\; <mo\; stretchy="false">\; (\; </mo>2}}^{\mathcal{l}}-\mathrm{1\; <mo\; stretchy="false">\; )\; </mo>}$ , we have $e_1=e_0=2^{\mathcal{l}}-1$ , which implies $\tilde{e}=0$ . Thus T is Tribonacci cordial.

Theorem 2.19 $P_n^2$ is Tribonacci cordial.

Proof. Let us identify the vertices of the graph as $V(P_n^2)=\{v_1,v_2,\cdots ,v_n\}$ . We define labeling $f\mathrm{<mo>\; :\; </mo>}V\mathrm{<mo\; stretchy="false">\; (\; </mo>}{P}_n^2\mathrm{<mo\; stretchy="false">\; )\; </mo>}\to \mathrm{<mo>\; \{\; </mo>}{T}_0\mathrm{,}{T}_1\mathrm{,}{T}_2\mathrm{,}\cdots \mathrm{,}{T}_n\mathrm{<mo>\; \}\; </mo>}$ as follows:

$f\mathrm{<mo\; stretchy="false">\; (\; </mo>}{v}_i\mathrm{<mo\; stretchy="false">\; )\; </mo>}=(\begin{array}{ll}{T}_{i-2}\mathrm{,}\hfill & \text{if}q=0\hfill \\ T_{i-1}\mathrm{,}\hfill & \text{if}q=\mathrm{1,2}\hfill \\ T_i\mathrm{,}\hfill & \text{if}q=3\hfill \end{array}$

where $i=4p+q$ . Clearly this labeling generates $e_1=n$ and $e_0=n-1$ , hence $\tilde{e}=1$ , which proves the theorem.

Theorem 2.20 $C_n^2$ is Tribonacci cordial only for $n\equiv 0(\mathrm{mod}2)$ .

Proof. First we note that, for any two Tribonacci labeling $f\mathrm{<mo>\; :\; </mo>}V\mathrm{<mo\; stretchy="false">\; (\; </mo>}{C}_n^2\mathrm{<mo\; stretchy="false">\; )\; </mo>}\to \mathrm{<mo>\; \{\; </mo>}{T}_0\mathrm{,}{T}_1\mathrm{,}\cdots \mathrm{,}{T}_n\mathrm{<mo>\; \}\; </mo>}$ and $g\mathrm{<mo>\; :\; </mo>}V\mathrm{<mo\; stretchy="false">\; (\; </mo>}{C}_n^2\mathrm{<mo\; stretchy="false">\; )\; </mo>}\to \mathrm{<mo>\; \{\; </mo>}{T}_0\mathrm{,}{T}_1\mathrm{,}\cdots \mathrm{,}{T}_n\mathrm{<mo>\; \}\; </mo>}$ , ${\tilde{e}}_f-{\tilde{e}}_g\equiv 0(\mathrm{mod}4)$ . We omit the proof as it is very similar to Theorem 2.2. Now observe that when n is odd, i.e., $n=2k+1$ , $|E(C_n^2)|=4k+2$ , thus ${\tilde{e}}_{C_n^2}\equiv 2(\mathrm{mod}4)$ . For the case n being even, let $v_1\mathrm{,}{v}_2\mathrm{,}\cdots \mathrm{,}{v}_n$ be the vertices of the graph $C_n^2$ . We define the following function that assigns labelings to the vertices.

$f\mathrm{<mo\; stretchy="false">\; (\; </mo>}{v}_i\mathrm{<mo\; stretchy="false">\; )\; </mo>}=(\begin{array}{ll}{T}_{i-2}\mathrm{,}\hfill & \text{if}q=0\hfill \\ T_{i-1}\mathrm{,}\hfill & \text{if}q=\mathrm{1,2}\hfill \\ T_i\mathrm{,}\hfill & \text{if}q=3\hfill \end{array}$

where $i=4p+q$ . Clearly this labeling generates $e_1=e_0=n$ , hence $\tilde{e}=0$ , which proves the theorem.

Conflicts of Interest

The authors declare no conflicts of interest regarding the publication of this paper.

References

[1]	Cahit, I. (1987) Cordial Graphs: A Weaker Version of Graceful and Harmonious Graphs. ARS Combinatoria, 23, 201-207.
[2]	Gallian, J.A. (2019) A Dynamic Survey of Graph Labelling. Electronic Journal of Combinatorics. https://doi.org/10.37236/27
[3]	Rokad, A.H. and Ghodasara, G.V. (2016) Fibonacci Cordial Labeling of Some Special Graphs. Annals of Pure and Applied Mathematics, 11, 133-144.
[4]	Mitra, S. and Bhoumik, S. (2020) Fibonacci Cordial Labeling of Some Special Families of Graphs. Annals of Pure and Applied Mathematics, 21, 135-140. https://doi.org/10.22457/apam.v21n2a9663
[5]	Rokad, A.H. (2017) Fibonacci Cordial Labeling of Some Special Graphs. Oriental Journal of Computer Science and Technology, 10, 824-828. https://doi.org/10.13005/ojcst/10.04.18