Stochastic Quantum Hydrodynamic Model from the Dark Matter of Vacuum Fluctuations: The Langevin-Schrödinger Equation and the Large-Scale Classical Limit ()

1. Introduction
The conflict between the quantum mechanics and the classical ones attracts the interest of many researchers of the noways physics [1] - [16].
This lack of knowledge has lead to many logical paradoxes that contrast with our sense of reality [1] [2] [3]. A quantitative tentative to investigate the problem was given by Bell [3] in response to the so-called EPR paradox [2], a critical analysis of the quantum non-locality respect to the notion of the macroscopic classical freedom and local relativistic causality.
The Copenhagen interpretation of quantum mechanics [3] [4] [5] treats the wave function as representing “the probability” of finding a particle at some location’ [12]. However, such a treatment leads to the non-intuitive conclusion that the physical state is just a probability wave until observed. The absence of an analytical link with the pre-measure physical state fights against the common sense of reality and the existence of a real world independent by the observer and the measure process [5].
If the Copenhagen probabilistic connection with the pre-measure world is strictly assumed, the conclusion that the real state is not physically defined before the measure is unavoidable.
Actually, the completeness and self-consistency of this logical result cannot be achieved since the process of the observation is out of the Hamiltonian description of quantum mechanics. The need of having a classical environment in order both to perform the measure and to define the quantum eigenstates, indeed, leads to a great theoretical loophole: Is the classical world necessary to the quantum mechanics or the quantum evolution is the fundamental law?
Besides, the unavailability of the theoretical connection between the quantum and the classical mechanics, that would explain how the laws of physics pass from the deterministic quantum behavior to the classical one (even irreversible), leaves open many questions about how concepts of the classical experience such as, measure, principle of causality, locality, physical state of the external reality, wave and particle behaviors, can be compatible or related to the quantum mechanics.
The connection between the quantum state and the statistical (classical) process of measure is defined by a postulate that, is a matter of fact, makes the quantum mechanics a semi-empirical theory without a self-consistent theoretical framework.
On the other hand, if the wave function is something physically real, then, there must exist a defined mechanism (e.g., the so-called wave function collapse, out of the canonical law of quantum mechanics) expressing the interaction with the observer embedded into a classical universe.
In this case, there also exists the problem about how the Schrödinger equation can be generalized [13] [14] or derived in the frame of such a more general quantum theory [15].
In order to fill this theoretical lack, there exist various interpretations of quantum mechanics like the many-worlds interpretation [17], the Bohmian mechanics [18] [19], the modal interpretation [20], the relational interpretation [21], the consistent histories [22], the transactional interpretation [23] [24], the QBism [25], the Madelung quantum hydrodynamics [26] [27] [28] and the decoherence approach [29].
The Madelung approach (that is a particular case of the Bohmian mechanics [30]) owns the important peculiarities to be both mathematically equivalent to the Schrödinger one [31] and to treat the wave function evolution 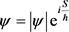 in the classical-like representation as the motion of the mass density
owing the impulse
. In this way it introduces the concept of trajectories of motion and naturally hosts the notion of physical reality before the measure.
in the classical-like representation as the motion of the mass density
owing the impulse
. In this way it introduces the concept of trajectories of motion and naturally hosts the notion of physical reality before the measure.
The Madelung description has the advantage of disembogues into the classical mechanics as soon as
and the so-called quantum pseudo-potential are set to zero.
Nevertheless, if we wipe out (by hand) the quantum potential from the quantum hydrodynamic equations in order to obtain the classical mechanics, we also cancel the stationary quantum eigenstates where the total force exerted by the Hamiltonian potential and the quantum one (on the mass density distribution
) is null. Doing that, we change the nature of the equation of motion. Thence, a more correct and analytic mechanism is needed to pass from the quantum non-local description to the classical one in the frame of the hydrodynamic approach.
Other characteristics of the quantum to classical transition are captured by the decoherence approach that investigates the possibility of obtaining the classical state through the loss of quantum coherence generated by the presence of the environment. The decoherence is shown to be produced into the system by treating it as a sub-part of the overall system, comprehending the environment whose interaction is semi-empirically defined by non unitary interaction [29]. However, this approach is not able to explain how, by having a quantum overall system, the observer can perform the irreversible processes of the statistical measure (and to be quantum de-coupled with the measured system). To overcome this problem, the relational quantum mechanics introduces the super-observer that is not entangled with the overall system [21]. Actually, this “ad hoc” postulate, is unsatisfactory and brings logical contradictions.
From the experimental and numerical simulation point of view, there exist the important evidence that the decoherence and the localization of quantum states come from the interaction with the stochastic fluctuations of the environment [32] [33] [34] [35] and/or dark matter.
In this work the authors generalize the Madelung quantum hydrodynamic approach to its stochastic version, where the noise, due to the quantum-mechanical properties of a fluctuating vacuum (in term of curvature associated to dark matter), owns a non-white spectrum showing the emergence of the intrinsic De Broglie physical length into the vacuum.
The work also shows that the stochastic Langevin-Schrodinger equation is derived from the theory for systems whose physical length is much smaller than the De Broglie length.
In the final section the authors analyze how the classical mechanics can be achieved, under appropriate conditions, on a large scale description. The uncertainty principle in the measure process is investigated in the frame of the stochastic quantum hydrodynamic model (SQHM). The paper analyzes how the measure in a classical large-scale system can satisfy both the uncertainty principle and the finite velocity of transmission of light and information.
2. The Quantum Hydrodynamic Equation in Presence of Vacuum Dark MASS Density Fluctuations
In the present work we go beyond the flat static solution
as for classical matter vacuum, and assume that there is still energy and momentum within the space-time due to the possible presence of gravitational waves that can give a contribution
. Solution to such equations has been introduced by De Sitter that illustrates that matter may not be the only source of gravity and thus wrinkles in the space-time may not be due to matter only.
By considering the vacuum as a fluctuating background, we define the stochastic generalization of the quantum-hydrodynamic equations [26] [27] [28] [31] that for the wave function
are given by the conservation equation for the mass density
. (2.1)
where the velocity
is defined, through the momentum
, by the motion equations
, (2.2)
, (2.3)
where
, where H is the Hamiltonian of the system and where
, (2.4)
The ripples of the vacuum curvature are assumed to manifest themselves by an additional fluctuating mass density distribution (MDD)
(2.5)
where
, that, through the quantum potential
, (2.6)
leads to the fluctuating force
. (2.7)
Being the mass density
defined positive, the vacuum fluctuations (as a mean
) give rise to an additional mass that, owning just the gravitational interaction, is dark matter.
For the purpose of this work, we assume that the vacuum dark matter (DM) does not interact with the physical system (the gravity interaction is disregarded for its weak constant and it is not included in H). As far as concerning the dark matter evolution, it is defined by additional (gravitational) motion equation descending by the cosmological dynamics. Nevertheless, we disregard the DM cosmological evolution and assume, for our laboratory macroscopic systems, that the dark mass
is locally uniformly distributed with a constant amplitude of fluctuations
such as
(2.8)
2.1. Spectrum and Correlation Function of the Dark-Matter-Induced Mass Density Fluctuations
In deriving the characteristics of the quantum potential fluctuations (and hence of its force), we use the condition that the vacuum dark matter, described by the wave function
, does not interact with the physical system (this due to the weak gravity constant). In this case the wave function
of the overall system reads
(2.1.1)
leading to the overall quantum potential
(2.1.2)
Moreover, given the energy fluctuations
, (2.1.3)
due to the vacuum dark mass density noise of wave-length
(2.1.4)
(associated to the dark matter wave-function fluctuation
(2.1.5)
where
(2.1.6)
at small wave length (
), reads
(2.1.7)
where it has been used the normalization condition
and where, on large volume, it has been used the approximation
. (2.1.8)
The result (2.1.7) shows that the energy, due to the mass density fluctuations, increases as the inverse squared of
.Being so, the associated quantum potential fluctuations, on very short distance (i.e.,
), can lead to unlimited large energy fluctuations even in the case of vanishing noise amplitude (i.e.,
).
In order to warrant the convergence of Equations (2.2-3, 2.6) to the deterministic limit (2.2-4) of quantum mechanics for
, this behavior imposes the need of a supplemental condition on the spatial correlation function of the noise (we name it
).
The derivation of conditions on the noise correlation function shape
, brings a quite heavy stochastic calculation [36]. A more simple and straight derivation of
can be obtained by considering the spectrum of the fluctuations.
Since each component of spatial frequency
brings the quantum potential energy contribution (2.1.6), the probability of happening
, (2.1.9)
by (2.1.7) reads
(2.1.10)
where
(2.1.11)
is the De Broglie length.
From (2.1.10) it comes out that the spatial frequency spectrum
(2.1.12)
is not white and the components with wave-length
smaller than
go quickly to zero.
Thence, given the mass density noise correlation function, that for the sufficiently general case, to be of practical interest, can be assumed Gaussian with null correlation time, isotropic into the space and independent among different co-ordinates such as
, (2.1.13)
the spatial shape
reads
(2.1.14)
The expression (2.1.14) shows that uncorrelated MDD fluctuations on shorter and shorter distance are progressively suppressed by the quantum potential allowing the deterministic quantum mechanics to realize itself for systems whose physical length is much smaller than the De Broglie one.
2.2. The STOCHASTIC Potential Approach
The characteristics of the stochastic force noise induced by the fluctuations of the quantum potential (due to the vacuum mass density fluctuations) can be derived by assuming the quantum potential as composed by a regular part
(to be defined) plus the zero mean fluctuating part
such as
. (2.2.1)
Moreover, given the force noise
, (2.2.2)
it is possible to show (see appendix A) that it owns the correlation function
(2.2.3)
with the condition
(2.2.4)
where the spatial shape
is connected to
of the dark matter and where T is the fluctuation amplitude parameter (of DM). Thence, the motion equation acquires the form
, (2.2.5)
, (2.2.6)
2.3. Correlation Function of the Quantum Force Fluctuations for De Broglie-Length Small-Scale Systems
As shown in Appendix A, the correlation function of the quantum potential fluctuations, at the smallest order in
, reads
(2.3.1)
where
is the boson-boson s-wave scattering length for Lennard-Jones interacting particles (see (3.6) in section 3).
By using the variance (2.3.1), for systems, whose physical length
is much smaller than the De Broglie length (i.e.,
), it follows that
(2.3.2)
where
(2.3.3.)
where
Besides, about the regular part
, for microscopic systems, without loss of generality, we can pose
(2.3.4)
where the spatial probability mass density (PMD)
reads
(2.3.5)
where
(2.3.6)
(where
is the PTF of the phase space Smolukowski equation (see (C.3) in Appendix C) for the Brownian process
, (2.3.7)
where, as shown in Appendix B, at first order of approximation in
, the term
generates
(2.3.8)
and where
.
Moreover, the relation between the friction coefficient
and the diffusion coefficient D, at the first order in the series expansion
, (2.3.9)
can generally read
(2.3.10)
where
is a numerical parameter that measures how the quantum hydrodynamic trajectories of motion are perturbed by fluctuations (leading to quantum decoherence and to energy dissipation). This parameter is specific for each considered system since the sensibility of the system to fluctuations is related to the Lyapunov exponents of their classical trajectories of motion. This aspect goes beyond the purpose of this work and (2.3.10) is semi-empirically assumed here.
For
we have a system that maintains the quantum coherence with no dissipation (e.g., as happens in the deterministic limit).
For
we retrieve the Einstein relation
that holds for the so called “dust matter” (the mass density, constituted by monomolecular dust, representing the classical MDD limit of the Madelung quantum hydrodynamics [31]).
In the general case of a system submitted to fluctuations, neither in quantum deterministic limit nor in the classical one, we assume that
.
In order the SQHM theory comprehends the canonical quantum mechanics in the deterministic limit (i.e.,
, where
is the physical length of the system), it must hold both that
(2.3.11)
and that
. (2.3.12)
Given that, by (2.3.2)
(2.3.13)
we obtain
(2.3.14)
, (2.3.15)
That, by posing
(with
) (2.3.16)
leads to
(2.3.17)
. (2.3.18)
Moreover, by assuming in the limit of small fluctuations amplitude
, (2.3.19)
it follows that
(2.3.20)
, (2.3.21)
so that (2.3.11-12) are satisfied by
. (2.3.22)
For instance, for
and
it follows that
(2.3.23)
, (2.3.24)
; (2.3.25)
For
and
, we obtain
(2.3.26)
, (2.3.27)
(2.3.28)
Furthermore, by posing
(2.3.29)
and
(2.3.30)
where
is the dimensionless constant
, (2.3.31)
that for
reads
(2.3.32)
and for system that satisfies the condition
that warrants
, (2.3.23-4, 2.3.26-7)) gives
. (2.3.33)
2.4. The Generalized Langevin-Schrödinger Equation for De Broglie-Length Systems
The quantum-hydrodynamic Equation (2.3.7) for the complex field
(2.4.1)
where
(2.4.2)
reads
(2.4.3)
leading to the partial stochastic differential equation
(2.4.4)
Introducing the Environment
The presence of unnoticeable small dark matter fluctuations, even negligible on the ordinary scale systems, is sufficed to lead to a finite De Broglie length that is much smaller than the cosmological scale allowing the quantum decoherence and the emergence of the classical behavior into the universe.
The possibility of dividing the universe in classical sub-parts, allows to correctly introduce the existence of the environment. Besides, given that the action of force noise of the environment on the MDD derivatives generates an increase of the energy of the quantum potential in the same way as the dark matter, it follows that the spatial shape of the correlation function of the force noise of the environment owns the same form of that one of the dark matter.
Thence, in presence of the physical environment it is possible to assume the stochastic interaction
(2.4.1.1)
from which it follows that
(2.4.1.2)
where, by assuming both
.and
, it follows that
(2.4.1.3)
and
, (2.4.1.4)
and that all preceding formulas can be retained with the substitution
(2.4.1.5)
(2.4.1.6)
It must be noted that, in absence of dark matter fluctuations, the quantum-decoupling of the environment cannot be assumed and that
cannot be formulated in the form of (2.4.1.1). Thence, (2.4.1.5-6) can be assumed only in a physical vacuum that, following the general relativity, is constituted by a fluctuating geometrical background.
2.5. The Langevin-Schrödinger Equation
Once the dark matter makes possible to have the classical environment, a system of microscopic physical length
(i.e.,
) obeys to the conservation Equation (see (C.3.9, C.3.11) in appendix C)
(2.4.1.7)
where (see ( C.3.11) in appendix C)
(2.4.1.8)
and where it has been used the identity
. Thence, by (2.4.1.7) it follows that
(2.4.1.9)
leading to the generalized Langevin-Schrodinger equation (LSE)
(2.4.1.10)(C.2.7)
Robust Quantum Systems and the Canonical LSE
Moreover, since for a quantum system that owns
and hence
, able to strongly maintain its quantum coherence (we name it “robust” quantum systems), it holds
, (2.4.2.1)
and, for
(2.4.2.2)
(e.g.,
for
and
), also that
, (2.4.2.3)
for sufficiently small temperature, the term
can be disregarded in (2.4.1.10) and the LSE reads
.(2.4.2.4) (LSE)
As already observed, the sensibility of the system to fluctuations is related to the Lyapunov exponents of its classical trajectories of motion. Thence, that for linear systems (non classically chaotic)
and the (LSE) can be applied to them.
Generally speaking, for the case of classically chaotic systems, the LSE (2.4.1.10) has to be considered.
Moreover, it must be noted that the SLE description is made possible by the integrability of the velocity field
that can be warranted in small scale (slightly perturbed) quantum system but it may fall in macroscopic large-scale system whose velocity field can be non-integrable.
2.6. The SQHM with Adiabatic Elimination of Fast Variables
For slow kinetics with the characteristic time
satisfying the condition
, (2.5.1)
Equation (2.3.7) (for
) reduces to
(2.5.2)
that for
reads
(2.5.3)
For a quantum system with
and
, equation (2.5.2) can be applied to kinetics with characteristic time down to
(2.5.4)
that being
(2.5.5)
gives
(2.5.6)
It is worth mentioning that Equation (2.5.3) leads to a simplified Smolukowski equation that is only a function of the space variables [37].
3. Emerging of the Classical Behavior on Coarse-Grained Large Scale
Is matter of fact that, if the quantum potential is canceled by hand in the quantum hydrodynamic equations of motion (2.1-3), the classical mechanical equation of motion emerges [28]. Even if this is true, this operation is not mathematically correct since it changes the characteristics of the QHA equations. Doing so, the stationary configurations (i.e., eigenstates) are wiped out because we cancel the balancing of the quantum potential force against the Hamiltonian force [37] that generates the stationary condition. Thence, an even small quantum potential cannot be neglected into the deterministic QHA model.
On the contrary, in the SQHM it is possible to correctly neglect the quantum potential (at least in classically chaotic systems) when its force is much smaller than the noise
such as
. (3.1)
When the non-local force generated by the quantum potential is quite small (respect to the fluctuations amplitude) so that
, (3.2)
its effect can be disregarded in (2.3.7).
Besides, even if the noise
has zero mean, the mean of the quantum potential fluctuations
is not zero, and the stochastic sequence of inputs of noise alters the coherent reconstruction of the quantum superposition of state by the dissipative force
in (2-3-7). Moreover, by observing that
(3.3)
grows with the scale of the system (i.e.,
for macroscopic systems), condition (3.2) is satisfied if
(3.4)
and the classical behavior can emerge in systems of sufficiently large physical length. Actually, in order to have a large-scale description, completely free from quantum effects, we can more strictly require
. (3.5)
By observing that for linear systems
, (3.6)
from (3.6) the SQHM shows that they do never have a macroscopic classical phase. Generally speaking, stronger the Hamiltonian potential higher the wave function localization and larger the quantum potential behavior at infinity [38]. Given the MDD
(3.7)
where
is a polynomial of order k, in order to have a finite quantum potential range of interaction it must be
(it results
for uni-dimensional linear interaction). Actually, since the linear interaction is not maintained up to infinity (for energetic reason, a finite bound energy requires a weaker than linear interaction such as
), there exists a large-scale classical description when the physical length of the system is much larger than the range of linear interaction. A physical example comes from solids owning a quantum lattice. If we look at the intermolecular features where the interaction is linear, the behavior is quantum (such as the x-ray diffraction shows), but if we look at their macroscopic properties (e.g., low-frequency acoustic wave propagation) the classical behavior is shown.
For instance, systems that interact by the Lennard-Jones potential for which the long distance wave function reads [39]
(3.8)
that leads to the quantum potential
(3.9)
and to the quantum force
, (3.10)
the large scale classical behavior can appear [38] [40] in a sufficiently rarefied phase (see section 4.4).
It is interesting to note that in (3.9) the quantum potential acquires the form of the hard sphere potential of the pseudo potential Hamiltonian model of the Gross-Pitaevskii equation [15] [41] where
is the boson-boson s-wave scattering length.
By observing that, in order to fulfill the condition (3.5) a sufficient condition reads
, (3.11)
it is possible to define the quantum potential range of interaction [38]
(3.12)
that gives a measure of the physical length of the quantum non-local effects.
The convergence of the integral (3.11) for
is warranted for L-J type potentials since, near the equilibrium point (
), the L-J interaction is linear and being
it follows that
. (3.13)
3.1. From Micro to Macro Description
By discretizing the phase space conservation equation given by the current Equations (2.2.5-6, 2.4, 2.3.4, 2.3.8) for the system of N coupled particles [42], it is possible to obtain the quantum hydrodynamic master equation for a macroscopic system of a huge number of molecules. Such a theoretical model goes beyond the purpose of the present work and it is left to a future investigation.
Here, generally speaking we observe that, given the range of interaction of the quantum potential
, the De Broglie length
, and the system size
(
the mean available volume per molecule), we can generally distinguish the cases:
1)
2)
3)
4)
Typically, for the L-J potential the quantum potential range of interaction
extends itself a little bit further than the linear zone around the equilibrium position
(let’ say up to
).
By using this approximation for the L-J interaction, so that for
, (3.1.1)
and for
[39]
, (3.1.2)
reads
(3.1.3)
that, since for
and microscopic mass
,
, we obtain
(3.1.4)
Thence, the rarefied phases owing
, for particles interacting by a Lennard-Jones potential, is fully classic since the mean molecular distance
is much larger both than the De Broglie length and the quantum potential length of interaction
.
The second case
refers to dense phases (e.g., fluid phase) that still own a classical behavior since, as a mean, the particle is distant each-other more than the range of interaction of the quantum potential. The inter-particle distance mostly lies in the non-linear range of L-J interaction [38].
The case “3”
applies when the neighboring molecules lie in the linear range of the intermolecular potential at a distance smaller than the non-local quantum potential interaction
.
The observables on such physical scale show quantum behavior (e.g., the Bragg’s diffraction of the atomic lattice).
In the case “4”
, when the condensed fluid phase (i.e.,
) persists down to a very low temperature so that the De Broglie length becomes larger than the mean intermolecular distance (
for typical intermolecular distance of order of 10−9 m), the fluid shows an extreme decrease of molecular viscosity [38]. The super-fluidity is induced by the quantum potential interaction between the molecules [40]
By changing the temperature and, accordingly, both
and the mean inter-molecular distance
, we can have quantum-to-classic phase transition in the case iii and iv, respectively:
1)
(with
) solid-fluid transition with melting of crystalline lattice (e.g., ice -water transition [38])
2)
(with
) superfluid-fluid transition (e.g., He4lambda point [38] [40])
3.2. Measurement Process and Quantum Decoherence
The SQHM model shows that the measure is not necessarily a decoherent process by itself: The sensing part of the measuring apparatus (the pointer) and the measured system may have a canonical quantum interaction that, after the measurement when the measuring apparatus is brought to the infinity (at a distance much beyond
), ends. Then the reading and the treatment of the “pointer” state are done by the measurement apparatus: This process is practically a classic irreversible process (with a defined arrow of time) leading to the macroscopic output of the measure.
On the other hand, the decoherence is necessary for the measurement process in order to have, both before the initial time and after the final one, quantum-decoupling between the measurement apparatus and the system in order to collect a statistical ensemble of data from repeated measures.
3.3. Minimum Measurements Uncertainty
If for physical length much smaller than
any system approaches the quantum deterministic behavior and behaves as a wave so that its sub-parts are not independent each-other, it follows that in order to perform the measurement (with independence between the measuring apparatus and the measured system) it is necessary that they are far apart (at least) more than
and hence, for the finite speed of propagation of interactions and information, the measured process must last longer than the time
. (3.3.1)
For
the measurement time can be even bigger than (3.3.1) but not less.
Moreover, since higher the amplitude of the noise T lower the value of
and higher the fluctuations of the energy measurements
, it follows that the minimum duration of the measurement
multiplied by the precision of the energy measurement
has a lower bond.
Given the Gaussian property of the noise (2.3.2), we have that the mean value of the energy fluctuation, for unidimensional systems, is
. Thence, for the non-relativistic case (
) a particle of mass m owns an energy variance
(3.3.2)
from which it follows that
, (3.3.3)
It is worth noting that the product
is constant since the growing of the energy variance with the square root of T is exactly compensated the decrease of the minimum time
of measurement
The same result is achieved if we derive the experimental uncertainty between the position and momentum of a particle of mass m in the quantum fluctuating hydrodynamic model.
If we measure both the spatial position of a particle with a precision
(so that we are able to not perturb the quantum configuration of the measured system) and the variance
of the modulus of its relativistic momentum
due to the fluctuations that reads
(3.3.4)
we obtain the experimental uncertainty
(3.3.5)
If we measure the spatial position with a precision
, we have to perturb the quantum state. Due to the increase of the spatial confinement of the wave function (by increasing the environmental temperature or by an external potential), the increase of both the quantum potential energy and its fluctuations are generated so that the final particle momentum gets a variance
higher than (3.3.5).
It is worth mentioning that the SQHM leads to the minimum measurements uncertainty as a consequence of the relativistic postulate of finite speed of light and information.
Even if the quantum deterministic behavior (
) in the low velocity limit (
) leads to the undetermined inequalities
(3.3.6)
(3.3.7)
their product
(3.3.8)
remains defined and constitutes the minimum uncertainty of the quantum deterministic limit. Beside, (3.3.6) in the relativistic limit shows that the duration of the measurement process in the deterministic limit becomes infinite. Being it endless, it is not possible to perform it in the canonical quantum mechanical universe.
Moreover, since non-locality is confined in domains of physical length smaller than
and information cannot be transferred faster than the light speed (otherwise also the uncertainty principle will be violated) the local realism is obtained in the coarse-grained large scale physics and the paradox of a “spooky action at a distance [43] ” is limited on a distance of order of
or of
.
The above result holds for particles with rest mass different from zero, while for determining the length of non local interaction (entanglement) of the photon (
?) the relativistic generalization of the SQHM is required.
3.4. Field of Application of the SQHM
The stochastic quantum hydrodynamic theory able to describe how the quantum entanglement is maintained up to a certain distance (see (3.11-3.12)) and how it can be maximized (see (3.4-3.5) and comment below), can lead to important improvements in the development of materials for high-temperature superconductors and Q bits systems.
Moreover, the theory owing to a self-defined quantum correlation distance can be also very important in defining different regimes of chemical kinetics in complex reactions and phase transitions.
Besides, the SQHM can furnish an analytical self-consistent theoretical model for mesoscale phenomena and quantum irreversibility.
4. Conclusions
The stochastic quantum hydrodynamic model shows that in the physical fluctuating vacuum, the spatial spectrum of the noise is not white and it owns the De Broglie characteristic length. Due to this fact, the quantum entanglement is effective in systems whose physical length is much smaller than such a length. The model shows that the non-local quantum interactions may extend themselves up to a finite distance in the case of non-linear weakly bonded systems.
The Langevin-Schrodinger equation can be derived in the frame of the stochastic quantum hydrodynamic model by taking into account, at the first order of approximation, the effect of fluctuations on microscopic systems.
The derivation of the Langevin-Schrodinger equation from the general stochastic quantum hydrodynamic model makes clear its basic assumptions and its range of applicability limited to microscopic systems whose physical length is much smaller than the De Broglie one.
The stochastic quantum hydrodynamic model shows that the minimum uncertainty condition is satisfied during the process of measurement (that can have a finite duration) in a classical super-system if, and only if, interactions and information do not travel faster than the speed of light, making compatible the relativistic postulate (at the base of the large scale locality) with the non-local quantum interactions at the micro-scale.
The stochastic quantum hydrodynamic model makes compatible the hydrodynamic description of quantum mechanics with the decoherence approach showing that the quantum potential is not able to maintain the quantum coherence in presence of fluctuations, generating a frictional force leading to a relaxation process (decoherence) and to the decaying of the superposition of states that do not physically survive in macroscopic systems made up of molecules and atoms interacting by long-range weak potentials such as the Lennard-Jones one.
The stochastic quantum hydrodynamic model describes how the quantum dynamics realizes itself in a vacuum whose metric fluctuates. In this scenario, the canonical quantum mechanics is the limiting description achieved just in the flat static vacuum.
Figuratively, in a 3-dimensional space time, the space can be represented by the surface of a see with very small ripples (instead by a flat static plane), the non local interaction of quantum mechanics breaks down on large scale and, in huge systems of weakly bounded particles, the classical mechanics emerge.
Acknowledgements
I thank Danilo De Rossi Professor Emeritus at the University of Pisa, for the passionate and in-depth discussions on the matter.
Appendix A
In order to derive the correlation function of the quantum potential fluctuations, we assume that the dark matter density (MD) fluctuations
own an amplitude that is very much smaller than the MD of the physical system n and hence it follows that
(A.1)
where
. (A.2)
Therefore,
(A.3)
that since the mean value
is not random, leads to
(A.4)
that at first order in
reads
(A.5)
Given that the terms with first derivatives
and
give terms proportional to
, in the limit of
they are null and thence it follows that
(A.6)
and, given that
, for very low temperature, it follows that
(A.7)
As far as it concerns the quantum potential force fluctuations, the zero order term can be generally assumed of the form
(A.8)
Since
, for Lennard-Jones potential we have that
1)
(A.9)
where
is the boson-boson s-wave scattering length. (see (3.6) in section 3), and hence that
2)
(A.10)
for
.
Moreover, by assuming in the linear range of interaction for
, the Gaussian localization
(A.11)
where
, it follows that the diffusion coefficient owns a parabolic behavior
(A.12)
that tends to zero for
or
.
Moreover, given that
and that for
(i.e.,
) the ratio
reaches the lowest value (since about all the mass is localized there), the wave function is poorly perturbed by MDD fluctuations (and is well described by the deterministic quantum limit), we can assume (A.10) over all the space to obtain
(A.13)
As far as it concerns the force correlation function, in this case we obtain
(A.14)
Appendix B
The irreversible force induced by fluctuations in small scale systems
In order to obtain the explicit expression of the term
(B.1)
let’s start by Equation (2.2.6 )
(B.2)
that we can rearrange as
(B.3)
where the term
(B.4)
in (B.3) generates an additional acceleration respect to the deterministic case leading to a change of the velocity field
of the mass density. It is noteworthy that, in the deterministic case (B.4) becomes null and
(actually, in the limit of small fluctuations (i.e., small size systems), n is close to the value of the deterministic limit of the eigenstates).
Moreover, by observing that in the stationary states (i.e.,
, the analogouses of the eigenstates of the deterministic limit [37] (let’s name them quasi-eigenstates), the mean MDD
does not changes with time and both
(B.5)
and
, (B.6)
approaching the stationary state (i.e.,
) it follows that
,(B.7)
and thence, generally speaking, for small
, sufficiently close to the stationary quasi-eigenstates, (B.4) can be developed in the series approximation
(B.8)
where
is a stochastic noise whose mean
is defined by the stationary state condition
(B.9)
Thence, at first order in
, close to the deterministic limit of quantum mechanics (i.e.,
), leads to
(B.10)
to
(B.11)
where
(B.12)
The first order approximation (B.10) allows the Marcovian process to become self-consistent (independent by the dark matter evolution) reducing to and where
is defined by the Smolukowski Equation (C.3) in appendix C, of the Marcovian process (2.3.7).
Moreover, for system with irrotational velocity field (that admits the action function S) such as
, Equation (2.3.7) can read
(B.13)
that by posing
, (B.14)
leads to
, (B.15)
Besides, by comparing (B.15) with (2.3.4), it follows that
(B.16)
and that
(B.17)
Finally it interesting to note that, for
the quantum hydrodynamic equation of motion leads to the quantum Brownian particle given by [44]
. (B.18)
is recovered.
Unfortunately, the validity of (B.18) is not general since
is not constant.
This agrees with the results given in ref. [45] [46] that show that only in the case of linear harmonic oscillator, in contact with a classical heat bath, the friction
can be a constant. Besides, since in order to have the quantum decoupling with the environment (i.e., a classical super-system), the non-linear interaction is needed (see identity (3.5-6) of section 3), actually, the case
= constant is never rigorously possible except for the deterministic limit of the canonical quantum mechanics with
.
It can only approximately accepted for locally linear oscillators (non-linearly coupled to the environment) for which we can assume
.
Appendix C
The environmental Marcovian noise in presence of the quantum potential
Since
is postulated by the approximation (2.8) the determination of
as well as of all the model is not complete.
Nevertheless, once infinitesimal dark matter fluctuations have broken the quantum coherence on the cosmological scale (i.e.,
that for barionic particles with mass
, it is enough
) and the resulting classical universe can be divided in sub-parts (the Newtonian limit of gravity is sufficiently weak force for satisfying condition (3.5)), we can define the super-system made up of the system and the environment.
At this stage, we can disregard the vacuum fluctuations associated to the dark matter (i.e.,
) and consider the Markovian process (2.3.7)
, (C.1)
, (C.2)
In presence of the quantum potential the evolution of the MDD
due to the stochastic motion Equation (2.3.7)) depends by the exact sequence of the force inputs of the Marcovian noise.
On the other hand,, the probabilistic mass density (PMD)
of the Smoluchowski equation
(C.3)
for the Marcovian process (2.3.7) (where the PTF
represents the probability that an amount of the PMD)
at time t, in a temporal interval τ, in a point
, transfers itself to the point
[47]) is somehow indefinite since the quantum potential depends by the exact sequence of the inputs of the force noise.
Even if the connection between
and
cannot be generally warranted, the approximation (B.10) that reads
, (C.4)
introduces the linkage between
and
(C.5)
leading the motion equation
(C.6)
It is worth mentioning that the applicability of (C.6) is not general but it is strongly subjected to the condition of being applied to small scale systems with
that admit stationary states (
) whose MDD is sufficiently close to that of the deterministic eigenstates (i.e., small force noise amplitude) for which it is possible to assume that the collection of all MDD
configurations will reproduce the PMD
such as
(C. 7)
This assumption is at the basis of the relation (C,4) that expresses the connection between the PMD n and the MDD
(i.e., the information about
can be obtained by knowing n and
).
Besides, if the system is sufficiently close to the deterministic limit of the quantum mechanics (for which
(i.e., very small force noise amplitude) it is a sufficient condition) and it owns (irrotational [31]) stationary states (i.e., quasi-eigenstates) so that it is still quantum and. the action function S (as integral of the momentum field) exists, we have that
and
can be defined by knowing n and S.
C.1. The conservation equation of the Smolukowski equation in presence of the quantum potential
By using the method due to Pontryagin [47] the Smolukowski equation leads to the differential conservation equation for the PTF
, (C.1.1)
where the current
is given by the series of cumulants
(C.1.2)
where
(C.1.3)
and where
, (C.1.4)
being
.(C.1.5)
Moreover, for one particle problem or many decoupled particle system (e.g., linear oscillators)) it is possible the diagonal description
(C.1.6)
(C.1.7)
C.2.1. The non-Gaussian PTF generated by the quantum potential
, (25)(C.2.1.1)
where the current
is given by the series of cumulants [47]
(C.2.1.2)
(C.2.1.3)
where
(C.2.1.4)
that owns an infinite number of terms due to the presence of the quantum potential.
If on one hand, the continuity of the Hamiltonian potential warrants that velocities
are finite and
on very short time increment, on the other hand, since the quantum potential depends by the derivatives of
, it can lead to very high values of force also in the limit of very short time increment so that very far away points
can contribute to the probability transition function
and the cumulants higher than two cannot be disregarded in (C.2.1.3).
Thence, being the cumulants higher than two non-vanishing, the PTF
is not Gaussian and. and equation (C.1.1) does not reduce to the FPE.
C.3. The motion equation for the spatial densities
By integrating over the momenta, the conservation equation
(C.3.1)
(C.3.2)
(C.3.3)
(C.3.4)
where
, (C.3.5)
(C.3.6)
we obtain
(C.3.7)
that with the condition
and by posing
(C.3.8)
leads to
(C.3.9)
where
and where
(C.3.10)
(C.3.11)
gives the compressibility of the mass density distribution that is linked to the generation of entropy and quantum dissipation. Thence, Equation (C.3.9) can read
(C.3.12)