On the Ideological and Political Course of General and Special Solutions of Differential Equations ()

1. 引言
在全国高校思想政治工作会议上,习近平总书记强调:“要坚持把立德树人作为中心环节,把思想政治工作贯穿教育教学全过程,实现全程育人、全方位育人,努力开创我国高等教育事业发展新局面” [1]。在这一重要讲话精神指引下,高等院校的思想政治教育“思政课程”和“专业课程”同向同行协同育人的新局面。课程思政的核心是实现知识传授与价值引领的有效结合,解决教师“为谁教、教什么、教给谁、怎么教”,让学生清楚“应该在哪儿用力、对谁用情、如何用心、做什么样的人”,督促教师从教书育人向立德树人转变。只有教师立德树人、潜心问道和关注社会相统一,才能提高学生思想水平、政治觉悟、道德品质、文化素养,让学生成为德才兼备、全面发展的人才。
课程思政在上海首先提出,到目前已经过去了整整五年时间。五年来,专家学者提出了很多新的见解和有建设项目的意见和建议。但我们认为,课程思政的根在课,魂在思。如何通过课程来践行课程思政,滕跃民教授提出的课程思政的道法术器和薛中会教授提出的融合思想具有很好的指导意义和实践价值 [2] [3]。
微分方程作为大学经管类、理工类各专业(数学专业除外)开设的一门重要的必修课《高等数学》一个重要的知识点,具有“育人”的独特优势和微言显大义的思想价值。作为高校数学教师,也应自觉落实高等数学“与思想政治理论课同向同行,形成协同效应”的教育要求,积极进行“知识传授与价值引领相结合”的课程思政教学改革及探索,实现立德树人、润物无声。本文结合课堂教学课程思政改革实践,在分析课程思政融入高等数学教学的可行性的基础上,重点从数学哲学视角探讨高等数学与课程思政的有机融合。
2. 微分方程通解和特解的基本概念
众所周知函数是研究客观事物运动规律的重要工具。通过函数关系,建立事物之间的联系,进而探究事物发展的一般规律,在实践中具有重要意义。可在许多实际问题中,我们通常不能或者难于直接给出所需要的函数关系,但一般能给出含有所求函数的导数(或微分)或差分(即增量)的方程,这样的方程在数学上称为微分方程或差分方程,需要从这些方程中求出或者探索得到函数关系。下面先对微分方程的有关内容做一简单介绍。
在通用的《高等数学》教材中,一般是这样定义微分方程的“凡含有未知函数的导数或微分的方程,称为微分方程(differential equation)”。其中未知函数为一元函数的微分方程,叫常微分方程(ordinary differential equation),未知函数为多元函数的微分方程,叫做偏微分方程(partial differential equation)。为简单起见,本文只讨论常微分方程中的课程思政,下文如无特殊生命,所说微分方程就仅仅指常微分方程。常见的常微分方程的形式如下例子(1)-(2)。
(1)
(2)
如果将一个函数代入微分方程,能够使得该方程成为恒等式,则称这个函数为该微分方程的解(solution)。微分方程的解中含有任意常数,且相互独立的任意常数的个数与微分方程的阶数相同,这样的解叫做微分方程的通解(general solution)。由于通解中含有任意常数,所反映的是一类事物发展变化的普遍规律(所谓的共性),它还不能确切的反应某客观事物的特定规律(所谓的个性)。为此,要根据问题的实际情况和具体的问题以及确定这些常数的条件,这些条件一般称为定解条件、初始条件或边界条件。确定了通解中的任意常数后所得的解,称为微分方程的特解(particular solution),即适用于具体问题或具体情况的解,也就是解决方案 [4]。
值得注意的是,一般来说微分方程的通解可以包含它的所有解,或者在满足一定的条件下,微分方程的通解会包含微分方程所有解。但是并不是所有微分方程都有通解,有些微分方程只能通过数值方法来求解。从哲学上来讲就是事物发展的特例或者称之为特殊情况。
第二个需要注意的是通解中的任意常数有时是“不任意”。在常微分方程通解的定义中强调相互独立的任意常数,意指在通解中取一组给定的常数得到的函数都为对应常微分方程的解。其实,任意常数并非可以任意取值,如
是常微分方程
的通解,此时C取大于2的值就没有意义了。所以任意常数并不是一定可以取遍任意实数的,而且也不要求它一定要取遍实数,这个任意性应该在使得通解关系式有意义的范围内体现。任意不是任性,任意的解要满足实际情况和具体问题,说以不能是任性的。就数学本身而言,只要使得数学表达式具有数学上的存在即可,但是数学函数表达式要面对具体的问题才具有永久的生命力和应用价值。因而除了满足数学的函数的定义域和对应法则的要求之外,还要考虑具体的应用场景的条件限制。
3. 科学社会主义基本原理和中国特色社会主义理论
马克思主义是关于全世界无产阶级和全人类彻底解放的学说。它由马克思主义哲学、马克思主义政治经济学和科学社会主义三大部分组成,是马克思、恩格斯在批判地继承和吸收人类关于自然科学、思维科学、社会科学优秀成果的基础上于19世纪40年代创立的,并在实践中不断地丰富、发展的无产阶级思想的科学体系 [5]。
习近平新时代中国特色社会主义思想是马克思主义基本原理与中国实际和中国文化相结合的产物。它是在借鉴和融汇人类文明的一切优秀成果的基础上形成的东西文化交融的最新理论成果。习近平总书记在十九大报告中论述:“新时代中国特色社会主义思想,是对马克思列宁主义、毛泽东思想、邓小平理论、‘三个代表’重要思想、科学发展观的继承和发展,是马克思主义中国化最新成果,是党和人民实践经验和集体智慧的结晶,是中国特色社会主义理论体系的重要组成部分,是全党全国人民为实现中华民族伟大复兴而奋斗的行动指南,必须长期坚持并不断发展。”
4. 微分方程通解和特解的课程思政内涵
4.1. 微分方程的通解与特解的辩证关系
4.1.1. 微分方程的通解到特解体现了辩证唯物主义认识论的一般规律
寻求通解是人类解决本质上相似问题的通用方法,进而归纳所得的通解,或者称之为一般规律推广到具体的案例中,寻求特殊问题的解。因而在微分方程的求解过程中蕴含着大量的人类最处理和解决问题的方法,即归纳和演绎。从党中央的指导思想到地方各级政府的方案,从国家的大政方针到各级政府的具体蓝图,无不体现了通解和特解的辩证规律。
4.1.2. 微分方程的通解和特解关系体现了矛盾普遍性与特殊性的辩证关系
通解是这个方程所有解的集合,也叫作解集。特解是这个方程的所有解当中的某一个,也就是解集中的某一个元素。唯物辩证法告诉我们,事物矛盾的特殊性与普遍性是相互区别的,有着各自的内容。事物矛盾的普遍性指矛盾无所不在,无时不有,是事物的共性,它是无条件的、绝对的。矛盾的特殊性指矛盾着的事物及其各个方面都有其特点,是事物的个性,它是有条件的、暂时的,因而是相对的。共性与个性的辩证关系是指,共性寓于个性之中,个性又受共性的制约,共性和个性在一定条件下相互转化。从“互联网+”到“人工智能+”和“大数据+”思想的提出,到具体的“互联网 + 教育”、“人工智能 + 教育”和“大数据 + 教育”等,都体现处矛盾普遍性与特殊性的辩证关系,这方面的例子太多,不一一列举。
4.1.3. 微分方程的通解和特解关系是理论与实践的辩证关系
理论是普遍的、抽象的,而实践总是具体的、实际的和确定的。微分方程的通解对于解微分方程给出了一个通解指导下的方案,而微分方程的特解是在具体的初始条件或边界条件下的特例。如微分方程(1)的通解为
,其中C为任意实数。当面对一个实际问题是我们需要根据具体情况来确定C的取值,比如C = 3是一个具体的问题,而C = 5是另外一个具体的情况。众所周知,一国两制,即“一个国家,两种制度”,是中央政府为实现国家和平统一而提出的基本国策,是通解;即是中央政府在台湾问题上的主要方针,也是香港、澳门两个特别行政区所采用的制度。香港问题、澳门问题和台湾问题都是历史上遗留下来的问题,解决这些问题,实现国家统一,是中华民族的共同愿望。目前香港回归22年,澳门回归20年,都是在“一国两制”这个“通解”指引到取得符合香港和澳门的通解:《中华人民共和国香港特别行政区基本法》和《中华人民共和国澳门特别行政区基本法》。展望未来,我们必将在“一国两制”基本国策的指导下实现台湾问题的解决。这些又何尝不是通解和特解的具体事例!
4.1.4. 微分方程的通解和特解关系是抽象与具体的辩证关系
通解是抽象的,是所有特解的集合,而具体的特解仅仅是该集合中的一个元素而已。微分方程的通解是数学从事物的普遍性之中抽象出来的公式或者解的一般表现形式,这种表现形式只有在面临具体的问题时才能具有现实的意义和价值。世界是纷繁复杂的,万事万物有个有自己的不同,而作为具体的特解在获得特解的同时反过来丰富通解的内涵。党中央、国务院的方针政策不可能面面俱到,各级地方党委和政府的政策法规一定是在党中央思想和国务院政策法规指导下的因地制宜,同时各个地方的具体的实践,反过来丰富党中央和国务院的总的政策方针,如此不断“不忘初心,砥砺前行,方能实现中华民族的伟大复兴的中国梦” [6] [7]。
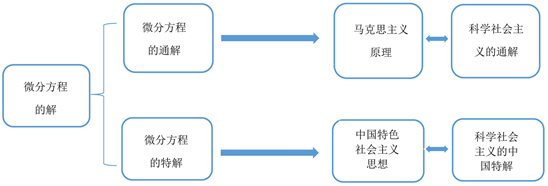
综上所述,微分方程的通解和特解的关系从哲学视角而言就是一般和具体、抽象和简单、共性和个性、理论与实践、归纳和演绎的关系。这些关系是马克思主义哲学的普遍话题,正如恩格斯所说数学是哲学的实践,哲学是数学的在思维层次的升华,并用来指导数学的发展。微分方程的通解和特解分别对应马克思主义原理的普适性和中国特色社会主义的特殊性;微分方程的特解是满足一定初始条件下的方程的通解中的特例;而中国特色社会主义是马克思、列宁主义与中国具体时间相结合的产物,可以外延的比喻为马克思、列宁主义在中国国情、民族特点和习惯、社会环境情况下的特解。从哲学层面上分析,二者都具有客观性,一个是自然的哲学,一个是社会的哲学。
5. 结束语
微分方程中蕴含着大量的立德树人的元素和思想,如何有效地提取数学知识中的立德树人因子是实现课程思政的关键。本文从微分方程通解和特解的关系出发,通过解析二者之间的哲学辩证关系,融马克思主义的普遍原理和习近平新时代中国特色社会主义理论体系的中国“特解”为一体,较为巧妙地阐释了道路的一般性和特殊性之间的关系。有利于立德树人根本目标的实现,有助于青年学子坚定立场和道路的自觉性。
基金项目
上海出版印刷高等专科学校2019年高教研究所立项课题:高职高专“人工智能 + 数学”人才教学改革研究,NO. SPPCGJS-16;上海出版印刷高等专科学校2019年度校内思政课题:人工智能 + 大思政视域下协同育人研究。2018年度教育部高校示范马克思主义学院和优秀教学科研团队建设项目(18JDSZK012);2019年上海出版印刷高等专科学校三期课程思政改革试点滚动支持项目。
参考文献
[1] 习近平谈治国理政[M]. 第二卷. 北京: 外文出版社, 2017.
[2] 滕跃民, 张玉华, 肖纲领. 高职专业“课程思政”的“道法术器”改革[J]. 辽宁高职学报, 2018(8): 53-61.
[3] 薛中会, 滕跃民, 马前锋, 周晓中. 从冰冷的美丽到火热的价值――矩阵思维下的社会主义核心价值观解读[J]. 辽宁高职学报, 2019, 21(3): 100-103.
[4] 刘雄伟, 王晓. 常微分方程通解, 特解, 所有解的区别与联系[J]. 大学数学, 2014 30(2): 88-90.
[5] 毛泽东思想和中国特色社会主义理论体系概论[M]. 北京: 高等教育出版社, 2018.
[6] 张景中. 数学哲学[M]. 北京: 中国少年儿童出版社, 2017.
[7] 吕亚男. 从数学文化视角探讨高等数学与课程思政的有机融合[J]. 西部学刊, 2019(2): 97-100.