On the Contribution of the Stochastic Integrals to Econometrics

Lewis N. K. Mambo^1,2, Rostin M. M. Mabela³, Isaac K. Kanyama^1,4, Eugène M. Mbuyi³

¹Department of Economics, University of Kinshasa, Kinshasa, Congo.
²Direction of Research and Statistics, Central Bank of Congo, Kinshasa, Congo.
³Department of Mathematics and Computer Science, University of Kinshasa, Kinshasa, Congo.
⁴Department of Economics and Econometrics, University of Johannesburg, Johannesburg, South Africa.

DOI: 10.4236/am.2019.1012073                

Abstract

The purpose of this paper is to present the theorical connection between the Itô stochastic calculus and the Financial Econometrics. This paper has two contributions. First, we give the backgrounds on how the stochastic calculus is used to model the real data with the uncertainties. Finally, by using Consumer Price Index (CPI) from the Central Bank of Congo and combining the Itô stochastic calculus and the AR (1)-GARCH (1, 1) model, we estimate the stochastic volatility of inflation rate measuring efficency of monetary policy. Thus the stochastic integrals are the powerful tools of mathematical modelling and econometric analysis.

Keywords

Stochastic Continuous-Time Models, Stochastic Volatility, AR (1)-GARCH (1, 1) Models, Inflation Rate

1. Introduction

In most dynamical systems which describe processes in economics, engineering, and physics, stochastic components and random noise are included. The stochastic aspects of the models are used to capture the uncertainty about the environment in which the systems are operating. For example, there are suggestions that increased uncertainty makes fiscal policy temporarily less effective [1]. Real life generates situations that require making a decision under uncertainty [2] [3] [4] [5]. By taking account of data uncertainty, the indiscriminate reduction of uncertaint observations to real numbers is avoided [5]. Uncertaint data implies information exhibiting inaccuracy, uncertainty and questionability [5]. The mathematical modeling of the uncertainty in economics and finance can be found in [2] [3] [5] - [12].

Therefore, the stochastic state space models and time series analysis have been both intensively and extensively developed during the past twenty years. A unified theory has been constructed during this period and the concepts and methods have been widely applied to problems in the area of engineering and communication, economics and management. Because of these developments, interest in stochastic state space model and its applications has greatly increased in econometric research.

This paper presents the stochastic integrals and numerics which permit successful mathematical modelling not only in econometrics but also in many other fields such biometrics, psychometrics, environment science, and hydrology, assuming of course that a suitable sequence of observed data is available.

For estimating the parameters of both stochastic continuous and discrete-time models, the methods of maximum likelihood are usually used by researchers because of its capacity to give the best unbaised estimators [9] [13] [14] [15] [16] [17].

The purpose of this paper is to emphasize on the linkage between the theory of stochastic integrals and time series analysis used in the econometric analysis [6] [16] [18] [19] [20] [21]. The stochastic integrals and numerics are considered as bridges that link the stochastic continuous-time models and the discrete time models [14] [18] [22] [23] [24] [25].

The structure of the paper is as follows. In Section 2 we will give the theory of stochastic integrals that is usefull to economic analysis. In Section 3 we give some stochastic differential equations used as econometric models that are used to express the economic theories. Section 4 gives some numerical methods to perform the empirical analysis. Section 5 illustrates the use of the stochastic integrals to time series econometric by estimating the stochastic volatility from the Autoregressive-Generalized Autoregressive Concoditional Heteroskedasticity model, that is, AR (1)-GARCH (1, 1) model.

2. Stochastic Integrals

Since the works of Kuyosi Itô the field of stochastic integrals attract the attention of many mathematicians and researchers [19] [26] - [33].

Itô Stochastic Integrals developed here are from [28] [29] [34] [35].

Definition 2.0.1 A process X is called adapted to the filtration ( ${\mathcal{F}}_t$ ), if for all t, $X\left(t\right)$ is ${\mathcal{F}}_t$ -measurable.

Proposition 2.0.1. (a) $X=\left(X_t\right)$, where $X_t$ is a d-dimensional measurable, ${\mathcal{F}}_t$ -adapted process is a continuous semimartingale if $X_t$ is continuous and has the form

$X_t=X_0+M_t+B_t$ (1)

for all t (a.s.), where $E\left|X_0\right|<\infty$, (1) $M=\left(M_t\right)$ is a continuous $L^2$ - ${\mathcal{F}}_t$ -martinagle with $M_0=0$ (a.s.) and (2) $\left(B_t\right)\in \mathcal{B}$.

(b) If in the decompostion 1, ( $M_t$ ), is a continuous local martingale and ( $B_t$ ) belongs to ${\mathcal{B}}_{loc}$, then ( $X_t$ ) will be called a continuous local semi-martingale.

Theorem 2.1. [35] [36] Let $X\left(t\right)$ be a regular adapted process such that with probability one ${\displaystyle {\int }_0^T}{X}^2\left(t\right)\text{d}t<\infty$. Then Itô integral ${\displaystyle {\int }_0^T}X\left(t\right)\text{d}B\left(t\right)$ is defined and has the following properties:

1) Linearity. If Ito integrals of $X\left(t\right)$ and $Y\left(t\right)$ are defined and $\alpha$ and $\beta$ are some constants then

${\displaystyle {\int }_0^T}\left(\alpha X\left(t\right)+\beta Y\left(t\right)\right)\text{d}B\left(t\right)=\alpha {\displaystyle {\int }_0^T}X\left(t\right)\text{d}B\left(t\right)+\beta {\displaystyle {\int }_0^T}Y\left(t\right)\text{d}B\left(t\right)\mathrm{.}$ (2)

2) ${\displaystyle {\int }_0^T}X\left(t\right)I_{\left(a\mathrm{,}b\right]}\left(t\right)\text{d}B\left(t\right)={\displaystyle {\int }_a^b}X\left(t\right)\text{d}B\left(t\right)$. The following two properties hold when the process satisfies an additional assumption

${\displaystyle {\int }_0^T}E\left(X^2\left(t\right)\right)\text{d}t<\infty \mathrm{.}$ (3)

3) Zero mean property. If condition 3 holds then

$E\left({\displaystyle {\int }_0^T}X\left(t\right)\text{d}B\left(t\right)\right)=\mathrm{0,}$ (4)

where E denotes expectation with respect to classical Wiener measure.

4) Isometry property. If condition 3 holds. Then

$E{\left({\displaystyle {\int }_0^T}X\left(t\right)\text{d}B\left(t\right)\right)}^2=E{\displaystyle {\int }_0^T}{X}^2\left(t\right)\text{d}B\left(t\right)$ (5)

Corollary 2.1.1. If X is a continuous adapted process then the Itô integral ${\displaystyle {\int }_0^T}X\left(t\right)\text{d}B\left(t\right)$ exists. In particular, ${\displaystyle {\int }_0^T}f\left(B\left(t\right)\right)\text{d}B\left(t\right)$ where f is a continuous function on $R$ is well defined.

A consequence of the isometry property is the expectation of the product of two Itô integrals as given in the following theorem.

Theorem 2.2. [36] Let $X\left(t\right)$ and $Y\left(t\right)$ be regular adapted processes, such that ${\displaystyle {\int }_0^T}X{\left(t\right)}^2\text{d}t<\infty$ and ${\displaystyle {\int }_0^T}Y{\left(t\right)}^2<\infty$. Then

$E\left({\displaystyle {\int }_0^T}X\left(t\right)\text{d}B\left(t\right){\displaystyle {\int }_0^T}Y\left(t\right)\text{d}B\left(t\right)\right)={\displaystyle {\int }_0^T}E\left(X\left(t\right)Y\left(t\right)\right)\text{d}t.$ (6)

where E denotes mathematical expectation.

We denote by ${ℝ}^{mn}$ all real-valued $m\times n$ matrices and by

$W\left(t\right)={\left(W_1\left(t\right)\mathrm{,}\cdots \mathrm{,}{W}_n\left(t\right)\right)}^{\prime }\mathrm{,}t\ge 0.$

Let $\left[a\mathrm{,}b\right]\in \left[\mathrm{0,}\infty \right[$ and we put

$C_W\left(\left[a\mathrm{,}b\right]\right)=\left\{f\mathrm{<mo>\; :\; </mo>}\left[a\mathrm{,}b\right]\times \Omega \to {ℝ}^{mn}\mathrm{<mo>\; |\; </mo>}\forall 1\le i\le m\mathrm{,}\forall 1\le j\le n\mathrm{<mo>\; :\; </mo>}{f}_{ij}\in C_{Wj}\left(\left[a\mathrm{,}b\right]\right)\right\}\mathrm{,}$

$C_{IW}\left(\left[a\mathrm{,}b\right]\right)=\left\{f:\left[a,b\right]\times \Omega \to {ℝ}^{mn}|\forall 1\le i\le m,\forall 1\le j\le n:f_{ij}\in C_{IWj}\left(\left[a\mathrm{,}b\right]\right)\right\}$

and $C_I\left(\left[a\mathrm{,}b\right]\right)$ respectively.

Definition 2.2.1. [37] If $f\mathrm{<mo>\; :\; </mo>}\left[a\mathrm{,}b\right]\times \Omega \to {ℝ}^{mn}$ belongs to $C_{IW}\left(\left[a\mathrm{,}b\right]\right)$, then the stochastic integral with respect to W is the m-dimensional vector defined by

${\displaystyle {\int }_a^b}f\left(t\right)\text{d}W\left(t\right)={\left({\displaystyle \underset{j=1}{\overset{n}{\sum }}}{\displaystyle {\int }_a^b}{f}_{ij}\left(t\right)\text{d}{W}_j\left(t\right)\right)}^{\prime }{}_{1\le i\le m}$ (7)

where each of the integrals on the right-hand side is defined in the sense of Itô.

Proposition 2.2.1. (Itô formula) [36] [38] Let $X_t=X_0+M_t+B_t$ be a d-dimensional continuous semimartingale. Let $F\in C_b^2\left({ℝ}^d\right)$, that is, let $F\mathrm{<mo>\; :\; </mo>}{ℝ}^d\to ℝ$ be bounded and continuous and have bounded, continuous derivatives of orders 1 and 2. Then,

$\begin{array}{c}F\left(X_t\right)=F\left(X_0\right)+{\displaystyle \underset{i=0}{\overset{d}{\sum }}}{\displaystyle {\int }_0^t}\frac{\partial F}{\partial x^i}\left(X_s\right)\text{d}{M}_s^i+{\displaystyle \underset{i=0}{\overset{d}{\sum }}}{\displaystyle {\int }_0^t}\frac{\partial F}{\partial x^i}\left(X_s\right)\text{d}{B}_s^i\\ +\frac{1}{2}{\displaystyle \underset{i=0}{\overset{d}{\sum }}}{\displaystyle {\int }_0^t}\frac{{\partial }^{2}F}{\partial x^i\partial x^j}\left(X_s\right)\text{d}{\langle M^i,M^j\rangle }_s\end{array}$ (8)

Stratonovich Stochastic Integrals. In [39], the multidimensional Stratonovich integrals $S_m\left(f\right)$ can be expressed by the following formula using Itô integrals

$S_m\left(f\right)={\displaystyle \underset{2k\le }{\sum }}\frac{m!}{2^{k}k!\left(m-2k\right)}{I}_{m-2k}\left(T{r}^{k}f\right).$ (9)

where $Tr$ denoted the iterated traces that are defined formally starting with

$Trf\left(s_1\mathrm{,}\cdots \mathrm{,}{s}_{m-2}\right)={\displaystyle \int }f\left(s_1\mathrm{,}\cdots \mathrm{,}{s}_{m-2}\mathrm{,}s\mathrm{,}s\right)\text{d}s\mathrm{.}$

Another approach to formula (9) using Hida’s theory of white noise. Working on ${ℝ}^m$ instead of ${ℝ}_{+}^m$ and assuming that f is a test-function, the integral $S_m\left(f\right)$ may indead be rewritten as

$\begin{array}{l}{\displaystyle \int }f\left(s_1,\cdots ,s_m\right){\stackrel{\dot{}}{X}}_{s_1}\left(w\right)\cdots {\stackrel{\dot{}}{X}}_{s_m}\left(w\right)\text{d}{s}_1\cdots \text{d}{s}_n\\ =\langle f,{\stackrel{\dot{}}{X}}^{\otimes n}\rangle \end{array}$

where the derivative of Brownian motion is understood in the distribution sense. In the sense of Hu and Meyer [39], a Stratonovich integral is given in rigorous form as

$S\left(f\right)={\displaystyle \underset{m}{\sum }}\frac{1}{m!}{\displaystyle {\int }_{\left[S\right)}}{f}_m\left(s_1,\cdots ,s_m\right)\text{d}{X}_{s_1}\left(w\right)\cdots \text{d}{X}_{s_m}\left(w\right)$ (10)

where f is a finite sequence of coefficients $f_m\in L_s^2\left({ℝ}^m\right)$ and $n!=n\times \left(n-1\right)\times \cdots \times 1$.

Itô’s Formula for Functions of Two Variables. If two processes X and Y both possess a stochastic differential with respect to and $f\left(x\mathrm{,}y\right)$ has continuous partial derivatives up to order two, then $f\left(X\left(t\right)\mathrm{,}Y\left(t\right)\right)$ also possesses a stochastic differential.

Theorem 2.3. [36] Let $f\left(x\mathrm{,}y\right)$ have continuous partial derivatives up to order two (a $C^2$ function) and X, Y be Itô processes, then

$\begin{array}{c}\text{d}f\left(X\left(t\right)\mathrm{,}Y\left(t\right)\right)=\frac{\partial f}{\partial x}\left(X\left(t\right)\mathrm{,}Y\left(t\right)\right)\text{d}X\left(t\right)+\frac{\partial f}{\partial y}\left(X\left(t\right)\mathrm{,}Y\left(t\right)\right)\text{d}Y\left(t\right)\\ +\frac{1}{2}\frac{{\partial }^{2}f}{\partial x^2}\left(X\left(t\right)\mathrm{,}Y\left(t\right)\right){\sigma }_X^2\left(X\left(t\right)\right)\text{d}t\\ +\frac{1}{2}\frac{{\partial }^{2}f}{\partial y^2}\left(X\left(t\right)\mathrm{,}Y\left(t\right)\right){\sigma }_Y^2\left(Y\left(t\right)\right)\text{d}t\\ +\frac{{\partial }^{2}f}{\partial x\partial y}\left(X\left(t\right)\mathrm{,}Y\left(t\right)\right){\sigma }_X\left(X\left(t\right)\right){\sigma }_Y\left(Y\left(t\right)\right)\text{d}t\end{array}$ (11)

An important case of Itô formula is for functions of the form.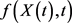

Theorem 2.4. [29] [36] [40] Let be twice continuously differentiable in x, and continuously differentiable in t (a 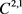function) and x be an Itô process, then

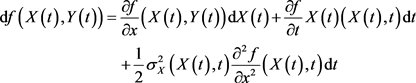(12)

Stochastic Calculus. Let 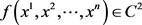and and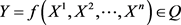. We denote by Q the totality of quasimartingales.

Definition 2.4.1. [36] For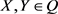, we say that X and Y are equivalent and write 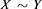if, with probability one,

for every.

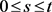The equivalence class containing X is denoted by dX and is called the stochastic differential of X. As known, by definition,

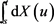
is the process.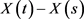

Let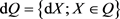, 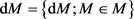and. We introduce the following operations in dQ [36].

(1) Addition: for.

(2) Product: for where and are the martingale parts of X and i respectively.

(3) B-multiplication: If and, then

is defined as an element in Q. Hence is defined from and dX. We define an element of dQ by.

Theorem 2.5. [36] The space dQ with the operations (1), (2) and (3) is a commutative algebra over B, i.e., a commutative ring with the operations (1) and (2) satisfying the relations

(a),

(b),

(c),

(d),

for and. We also have that, and.

If and, then and

(13)

where and are elements in B defined by and, respectively. If and, then is a d-dimensional Wiener process. Such a system of martingales is called a d-dimensional Wiener martingale.

(4) Symmetric Q-Multiplication

or and

Theorem 2.6. [35] [36] The space dQ with the operations (1), (2), (3) and (4) is a commutative algebra over Q; we have for,

where denotes Stratonovich product.

Theorem 2.7. If and, then for we have

(14)

The stochastic integral is called the Stratonovich integral or the Fisk integral or sometimes the Fisk-Stratonovich symmetric integral. Indeed, we have the following theorem:

Theorem 2.8. [36] For every X and Y in Q,

(15)

where denotes a partition and

,.

Skorokhod Integral. The Skorohod integral is an extension of the Itô integral to non-adapted processes and is the adjoint of the Malliavin derivative, which is fundamentals to the stochastic calculus of variations [41] [42].

Definition 2.8.1. [41] Assume that

(16)

Then we define the Skorohod integral of denoted by

by

(17)

where represents the Kronecker product.

Wick Product. The Wick product was introduced in Wick (1950) as a tool to renormalize certaint infinite quantities in quantum field theory. In stochastic analysis the Wick product was first introduced by Hida and Ikeda (1995). The Wick product is important in the study of stochastic differential equations. In general, one can say that the use of this product corresponds to and extends naturally—the use of the Itô integrals. The Wick product can be defined in the following way:

Definition 2.8.2. The Wick product of to elements

(18)

with is defined by

(19)

In the cas the basis independence of the Wick product can be seen from the following formulation of Wick multiplication in terms of multiple Itô integrals.

Proposition 2.8.1. Let. Assume that have the following representation in terms of multiple Itô integrals:

(20)

Suppose. Then

(21)

For the relation between the Wick multiplication and The Itô-Skorohod Integration we put for simplicity. One of the most stricking features of the Wick product is its relation to Itô-Skorokhod Integration. In short, this relation can be expressed as

(22)

Here the left hand side denotes the Skorokhod integral of the Stochastic process (which coincides with the Itô integral if is adapted), while the right hand side is to be interpreted as an -valued (Pettis) integral. The relation 22 explains why the Wick product is so natural and importnat in stochastic calculus.

3. Stochastic Differential Equations Models

The objective of this section presents in short the two main types of stochastic differential equation models. The theory of stochastic differential equation is very vaste and well known by Engineers and other scientists but less known and understood among economists. For further reading the reader can see [36] [43] - [48].

Example 1: Stochastic Differential Equation Model. Let be a diffusion in n dimensions described by the multidimensional stochastic differential equation

(23)

where is matrix valued function, is d-dimensional Brownian motion and and X and are n-dimensional vector valued functions. The vector and the matrix are the coefficients of the stochastic differential equation.

Theorem 3.1. [34] (Uniqueness and Existence of Solution) If the coefficients are locally Lipschitz in X with a constant independent of t; that is, for every N, there is a constant K depending only on T and N such that for all and all,

(24)

for any given the strong solution to stochastic differentional Equation (27) is unique. If in addition to condition 24 the linear growth condition holds

(25)

is independent of B, and, then the strong solution exists and is unique on, moreover,

where the constant C depends only on K and T.

The following theorem gives the solution of stochastic differential equations as Markov processes.

Theorem 3.2. [34] (The solution of SDEs as Markov processes) If equation 27 satisfies the conditions of the existence and uniqueness theorem 3.1, the solution of the equation for arbitrary initial values is a Markov process on the interval whose initial probability distribution at the instant to is the distribution of C and whose transition probabilities are given by

(26)

where is the solution of equation.

Theorem 3.3 [34] (The solution of SDEs as Diffusion processes) The condition of the existence and uniqueness theorem 3.1 are satisfied for the SDE

(27)

where, , and is a matrix. If in addition, the functions and are continuous with respect to t, the solution is a d-dimensional diffusion process on with drift vector and diffusion matrix. In particular, the solution of an autonomous SDE is always a homogeneous diffusion process on.

Example 2: Differential Equation with Markovian Switching Model. For economists, the economic phenomena can be governed by uncertainties and cycles. This model was developped by [49] as hybrid models. Consider the Stochastic Differential Equation with Markovian Switching of the form

(28)

Here the state vector has two components: and. The first one is normally referred to as the state while the second one is regarded as the mode. In its operation, the system will switch from one mode to another in random way, and the switching among the modes governed by the Markov chain.

Example 3: Differential with Respect to Fractional Brownian Motion Model. Let be a m-dimensional fractional Brownian motion of Hurst parameter. This means that the components of B are independent fractional Brownian motions with the same Hurst parameter H. For further reading see [46] [50] [51].

Consider the equation on

(29)

where is an m-dimensional random variable.

Assumption 3.3.1. Let us introduce the following assumptions on the coefficients:

A1. is differentiable in x, and there exists some constants and for every there exist such that the following properties hold:

A2. The coefficient satisfies for every

where), with and for some constant.

Consider the stochastic differential equation with respect to fBm (29) on where the process B is a d-dimensional fBm with Hurst parameter and is an m-dimensional random variable.

Suppose that the coefficients are measurable functions satisfying conditions A1 and A2, where the constants and may depend on, and,. Fix such that a uniue continuous solution such that for all. Moreover the solution is Holder continuous of order.

Example 4: Differential Equation with Jumps Models. In real world, some phenomena or economic policy decisions are governed under uncertainty with jumps. Therefore, stochastic differential equation with jumps modeling can be considered as a usefull econometric approach [32]. Consider a one-dimensional SDE, d = 1, in the form

(30)

for, with, and an -adapted one-dimensional Wiener process. We assume an an -adapted Poisson measure with mark space and with intensity measure, where is a given probability distribution function for the realizations of the marks. Consider a one-dimensional SDE with Jumps (30) in integral form, is of the form

(31)

Example 5: Partial Differential Equation Models. Stochastic Partial Differential Equation Models are used as power tools of mathematical modeling in many areas [52] [53] [54].

Consider the Itô Stochastic Partial Differential Equation of the form as mentioned in [27]

(32)

for, where, is an infinite dimensional Wiener process of the form

(33)

with independent scalar Wiener processes, and. Note that (Laplacian with Dirichlet boundary conditions) and in one spatial dimension has sample paths which are only -Hölder continuous. Here the family, , is an orthonormal basis in,.

Assumption 3.3.2. [27] (1) Linear operator A. Let be a finite or countable set. In addition, let be a family of real numbers with and let be an orthonormal basis of H. The linear operator is given by for all with. (2) Drift term F. Let be real numbers with and let be a globally Lipschitz continuous mapping. (3) Diffusion term B. Let be real numbers with and let be a globally Lipschitz continuous mapping. (4) Initial value: Let and be real numbers and let be an -measurable mapping with.

The literature contains many existence and uniqueness theorems for mild solutions of SPDEs. Theorem below provides an existence, uniqueness, and regularity result for solutions of SPDEs with globally Lipschitz continuous coefficients in the Equation (32).

Theorem 3.4. [27] Let Assumptions 3.3.2 (1)-(4) be fulfilled. Then there exists a unique of the Equation (32) that is predictable stochastic process

satisfying and

(34)

for all. In addition,.

4. Numerical Methods for Stochastic Differential Equations

In this section we give a brief review some numerical methods used in the stochastic analysis that can be usefull for economists and social scientists. These main books can help econometricians and economists to improve and understand the numerical methods for stochastic analysis [27] [45] [55] - [61]. The numerical methods for stochastic ordinary differential equations can be summarized as follows.

The Euler-Maruyama Scheme. We consider a scalar Itô stochastic ordinary differential equation (SODE) [27]

(35)

with a standard scalar Wiener process. The SODE (35) is in fact a symbolic representation for the stochastic integral equation

(36)

The simplest numerical scheme for the SODE (35) is the Euler-Maruyama Scheme given by

(37)

where one usually writes

for and where with is an arbitrary partition of.

The Milstein Scheme [27]. The another useful numerical scheme for the SODE (35) is the Milstein Scheme given by

(38)

Numerical Methods for Stochastic Differential Equations with Jumps. The Euler scheme for SDE with jumps (30), is given by the algorithm [32] [62] [63],

(39)

for with initial value. Here is the length of the time interval and is the n^th Gaussian distributed increment of the Wiener process W, , represents the total number of jumps of Poisson random measure up to time t, which is Poisson distributed with mean.

In the multidimensional case with mark-indepedent jump size we obtain the k^th component of the Euler scheme

(40)

Methods for Stochastic Partial Differential Equations. This material is from [64]

(41)

Methods for SPDE with Multiplicative Noise. Two representative numerical schemes used in the literature for the Stochastic Partial Differential Equation (32) are the linear-implicit Euler and the linear-implicit Crank-Nicolson schemes [27].

The Euler scheme

(42)

The Crank-Nicolson scheme

(43)

for and. Here it is necessary to assume that for all in Assumptions 2 in order to ensure that is inversible for every.

Convergence of SPDE with Multiplicative Noise. The convergence of the exponential Euler scheme will proved under the following assumptions.

Assumption 4.0.1. (A5) (Linear operator A). there exist sequences of real eigenvalues and orthonormal eigenfunctions of such that the linear operator is given by

for all with.

(A6) (nonlinearity of F). The nonlinearity is two times continuously Fréchet differentiable and its derivatives satisfy the following conditions

for all, , and, and

for all, where is a positive constant.

Let Q be a nonnegative definite symmetric trace-class operator on a separable Hilbert space K, be an ONB in K diagonalizing Q, and let the correspoing eigenvalues be. Let, , be a sequence of independent Brownian motion defined on filtered probability space. The process is called a Q-Wiener process in K.

(A7) (Cylindrical Q-Wiener process) There exist a sequence of positive real numbers and a real number such that

and pairwise independent scalar -adapted Wiener process for. The cylindrical Q-Wiener process is given formally by

(44)

(A8) (Initial value). The random variable satisfies, where is given in A7.

The convergence theorem for SPDE model 32

Theorem 4.1. (Convergence Theorem [27] ) Suppose that Assumptions 3 (A5)-(A8) are satisfied. Then there is a constant such that

(45)

holds for all, where is the solution of SPDE 32, is the numerical solution given by 42, for, and is the constant given in Assumption A8.

5. Application to Stochastic Volatility Estimation

Continuous-time models are central to financial econometrics, and mathematical finance. Here we estimate the Unobserved Stochastic Volatility of Inflation Rate. The literature on discrete-time models and that on continuous-time models were developed independently, but it is possible to establish connections between the two approaches [22] [23] [65] [66] [67] [68] [69].

In time series analysis, autoregressive integrated moving average (ARIMA) models have found extensive use since the publications of Box and Jenkins (1976) [25] [70] [71].

Maximum likelihood methods are widely used for estimating stochastic volatility [18].

To facilitate our discussion we will specialize the general continuous time model with zero drift, i.e.

(46)

(47)

where the stochastic processes, and are adapted. Here is a stationary process with nonnegative values and is called the stochastic volatility. The is the speed of adjustment of y to its long-run mean, , and is a positive scalar. And also is a standard Wiener process.

One should note that the constant elasticity variance process (CEV) in 47 implied an autoregressive model in discrete time for, namely:

(48)

(49)

After some algebraical manipulations such as, and and, , we have this hybrid model that has the autoregssive model and the generalized autoregressive condintionally heteroscedastic models, i.e. the AR (1)-GARCH (1, 1) Model with the mean equation [13] [19] [25] [70] [72] [73],

(50)

where, with following a t-Student distribution and the variance equation that can be presented as follows

(51)

where is a vector of two standard dimensional Brownian motions that are independent with zero mean and unit variance, and are defined on probability space.

In time series analysis, a process is called a GARCH(p,q) process if its first two conditional moments exist and satisfy [13]

(1),.

(2) There exist constants, and such that

Theorem 5.1. ( [13] Strict stationarity of the strong GARCH (1, 1) process) if

then the infinite sum

converges almost surely (a.s.) and the process () defined by is the unique strictly stationary solution of the model. This solution is nonanticipative and ergodic. If and, there exists no strictly stationary solution.

Another important theorem for our analysis is the secon-order stationarity of the GARCH (1, 1) process.

Theorem 5.2. Let. If, a nonanticipative and second-order stationary solution to the GARCH(1,1) model does not exist. If, the process () defined by (2.13) is second-order stationary. More precisely () is a weak, white noise. Moreover, there exists no other second-order stationary and nonanticipative solution.

To estimate the parameters of these models we use the maximum likelihood method. The maximum likelihood method provides the best estimators and efficient estimators [13] [73] - [78]. The density f of the strong write noise is assumed known. This assumption is obviously very strong. Conditionally on the -field generated by, the variable has the density. It follows that given the observations, and the initial values, the conditional likelihood is defined by

where the are recursively, defined for, by

For the student’s t-distribution, the log-likelihood contributions are of the form

where the degree of freedom controls the tail behavior and log denotes the natural logarithm, that is, log_e where. The t-distribution approaches the normal as and denotes the Gamma function.

A maximum likelihood estimator (MLE) is obtained by maximizing the likelihood on a compact subset of the parameter space [13] [79] [80] [81] that is,

(52)

To select a fitted model, the Akaike (1973) information criterion (AIC), Schowrz (1978) information (SIC), the mean squared error criterion (SIC), Hannan-Quinn information criterion (HQC) are usually used, that is,

where refers to the number of estimated model parameters.

where is the log-likelihood, k is the number of parameters, and n is the number of observations. Among a finite set of models; the model with the lowest criteria is preferred.

6. Empirical Results

In this study we modelize the stochastic volatility of inflation rate observed by the Central Bank of Congo for the period from January 2004 to June 2018. We get the inflation rate by transforming the consumer price index (CPI) index by using log-difference transformation, that is,. The operations of taking logarithms and differencing are standard time series tools for coering a data set into looking stationary (Resnick, 2007); therefore our variable is stationary. The inflation rate measures how fast prices are rising [21] [82]. For the period under analysis Table 1 shows that the mean, the maximum, and minimum inflation rates are 1.3, 11.4, −7.5 percentages respectively. (ii) With the Jarque-Bera statistic, 346.8773, it indicates that the inflation rate does not follow the normal distribution. It is well known that the fundamental task in many statistical analyses is to characterize the location and variability of a data set. A further characterization of the data includes skewness and kurtosis. The Skewness statistics is a measure of symmetry, or more precisely, the lack of symmetry. A distribution, or data set, is symmetric if it looks the same to the left and right of the center point. The Skewness of 1.52 indicates the moderate level.

In statistics, the Kurtosis is a measure of whether the data are heavy-tailed or light-tailed relative to a normal distribution. That is, data sets with high kurtosis tend to have heavy tails, or outliers. Data sets with low kurtosis tend to have light tails, or lack of outliers. Kurtosis statistics of the inflation rate 9.23 more large than 3, and Jarque-Bera statistics indicate that inflation rate does not follow the normal distribution. With high kurtosis statistic, 9.2287, there is an indication of inflation volatility.

We use a Student statistic test of statistical significance and find that parameters estimations are all statistically significant. Results confirm that the past volatilities affect the current volatility of inflation rate. Thus, we the dynmical behavior of volatility. We restrict the constant term to a function of the GARCH parameters and the unconditional variance:

where is the unconditional variance of the residuals, that is,.

Table 2 raises tree isues. First, in the mean equation, the coefficient measuring the persistence of inflation rate is high. This means that the monthly last inflation contributes to current rate by 66 percents. Secondly, the stochastic

Table 1. Summary statistics.

Table 2. Results of estimation.

volatility persistence of CPI-inflation rate is very high level, , this means that the past volatility information contributes to current volatility of inflation rate at 100 percents. Therefore the purchasing power of congolese householders is also volatile.

The postestmation tests of Ljung Box (1978), Q-Stat = 3.0639, and ARCH test, 0.0171, show that there are any remaining ARCH effects in the residuals.

7. Concluding Remarks

Since the Itô’s works, the stochastic integrals and stochastic differential equations attract the attention of many researchers in the fields of mathematical modelling. In this paper, we emphasize on the application of stochastic integrals and differential equations in the economics and finance. Comparing to discrete models, the stochastic continuous-time models have many advantages because they take into account the uncertainty. The limit of this approach is the complexity of stochastic calculus and stochastic numerical methods. As mentioned by scientists (see Wiener, Einstein, Itô) the uncertainties are anywhere and anytime; therefore the stochastic integrals must be well known and understood by all scientists.

Conflicts of Interest

The authors declare no conflicts of interest regarding the publication of this paper.

References

[1]	Berg, T.O. (2017) Business Uncertainty and the Effectiveness of Fiscal Policy in Germany. Macroeconomic Dynamics, 23, 1442-1470.
[2]	Basu, S. and Bundick, B. (2017) Uncertainty Shocks in a Model of Effective Demand. Econometrica, 85, 937-958. https://doi.org/10.3982/ECTA13960
[3]	Basu, S. and Bundick, B. (2018) Uncertainty Shocks in a Model of Effective Demand: Reply. Econometrica, 86. https://doi.org/10.2139/ssrn.3216683
[4]	Kubzun, A.I. and Kan, Y.S. (1996) Stochastic Programming Problems with Probability and Quantil Functions. John Wiley & Sons, New York.
[5]	Möller, B. and Reuter, U. (2007) Uncertainty Forecasting in Engineering. Springer, New York.
[6]	Sahalia, Y.A. (2002) Maximum Likelihood Estimation of Discretely Sampled Diffusions: A Closed-Form Approximation Approach. Econometrica, 70, 223-262. https://doi.org/10.1111/1468-0262.00274
[7]	Barndorff-Nielsen, O.E. and Shephard, N. (2004) Econometric Analysis of Realized Covariation: High Frequency Based Covariance, Regression, and Correlation in Financial Economics. Econometrica, 72, 885-925. https://doi.org/10.1111/j.1468-0262.2004.00515.x
[8]	Chernozhukov, V., Fernández-Val, I. and Luo, Y. (2018) The Sorted Effects Method: Discovering Heterogeneous Effects beyond Their Averages. Econometrica, 86, 1911-1938. https://doi.org/10.3982/ECTA14415
[9]	Hansen, L.P. (2012) Dynamic Valuation Decomposition within Stochastic Economies. Econometrica, 80, 911-967. https://doi.org/10.3982/ECTA8070
[10]	Hirano, K. and Wright, J.H. (2017) Forecasting with Model Uncertainty: Representations and Risk Reduction. Econometrica, 85, 617-643. https://doi.org/10.3982/ECTA13372
[11]	Van Horne, J.C. and Wachowicz, J.M. (2008) Fundamentals of Financial Management. 13th Edition, Financial Times/Prentice Hall, Upper Saddle River, NJ.
[12]	Stokey, N.L. (2009) The Economics of Inaction: Stochastic Control Models with Fixed Costs. Princeton University Press, Princeton, NJ. https://doi.org/10.1515/9781400829811
[13]	Francq, C. and Zakoian, J.M. (2010) GARCH Models Structure, Statistical inference and Financial Application. John Wiley and Sons, West Sussex. https://doi.org/10.1002/9780470670057
[14]	Lo, A.W. (1988) Maximum Likelihood Estimation of Generalized Itô Processes with Discretely Sampled Data. Econometric Theory, 4, 231-247. https://doi.org/10.1017/S0266466600012044
[15]	Prakasa Rao, B.L.S. (2010) Statistical Inference for Fractional Diffusion Processes. John Wiley and Sons, West Sussex.
[16]	Ait Sahalia Y. and Jacod, J. (2014) High-Frequency Financial Econometrics. Princeton University Press, Princeton, NJ. https://doi.org/10.23943/princeton/9780691161433.001.0001
[17]	Qin, L. and Linetsky, V. (2017) Long-Term Risk: A Martingale Approach. Econometrica, 85, 299-312. https://doi.org/10.3982/ECTA13438
[18]	Aït Sahalia, Y. and Kimmel, R. (2007) Maximum Likelihood Estimation of Stochastic Volatility Models. Journal of Financial Economics, 83, 413-452. https://doi.org/10.1016/j.jfineco.2005.10.006
[19]	Aït-Sahalia, Y. and Jacod, J. (2010) Is Brownian Motion Necessary to Model High-Frequency Data? The Annals of Statistics, 38, 3093-3128. https://doi.org/10.1214/09-AOS749
[20]	Aït-Sahalia, Y., Fan, J.Q., Laeven, R.J.A., Dan Wang, C. and Yang, X.Y. (2017) Estimation of the Continuous and Discontinuous Leverage Effects. Journal of the American Statistical Association, 112, 1744-1758. https://doi.org/10.1080/01621459.2016.1240082
[21]	Aït Sahalia, Y. and Matthys, F.H.A. (2018) Robust Consumption and Portfolio Policies When Asset Prices Can Jump. Journal of Economic Theory, 9. https://doi.org/10.2139/ssrn.2976562
[22]	Black, F. and Karasinski, P. (1991) Bond and Option Pricing When Short Rates Are Lognormal. Financial Analysts Journal, 47, 52-59. https://doi.org/10.2469/faj.v47.n4.52
[23]	Black, F. and Scholes, M. (1973) The Pricing of Options and Corporate Liabilities. The Journal of Political Economy, 81, 637-654. https://doi.org/10.1086/260062
[24]	Cox, J.C., Ingersoll Jr., J.E. and Ross, S.A. (1985) A Theory of the Term Structure of Interest Rates. Econometrica, 53, 385-407. https://doi.org/10.2307/1911242
[25]	Nelson, D.B. (1990) Stationarity and Persistence in the Garch(1,1) Model. Econometric Theory, 6, 318-334. https://doi.org/10.1017/S0266466600005296
[26]	Davis, R.A. and Song, L. (2012) Functional Convergence of Stochastic Integrals with Application to Statistical Inference. Stochastic Processes and their Applications, 122, 725-757. https://doi.org/10.1016/j.spa.2011.10.007
[27]	Jentzen, A. and Kloeden, P.E. (2011) Taylor Approximations for Stochastic Partial Differential Equations. The Society for Industrial and Applied Mathematics, Philadelphia, PA. https://doi.org/10.1137/1.9781611972016
[28]	Kuo, H.H. (2006) Introduction to Stochastic Integrals. Springer Science Business, New York.
[29]	Medvegyev, P. (2007) Stochastic Integration Theory. Oxford University Press, New York.
[30]	McKean Jr., H.P. (1969) Stochastic Integrals. Academic Press, New York. https://doi.org/10.1016/B978-1-4832-3054-2.50008-X
[31]	Platen, E. and Heath, D. (2006) A Benchmark Approach to Quantitative Finance. Springer-Verlag, New York. https://doi.org/10.1007/978-3-540-47856-0
[32]	Platen, E. and Bruti Liberti, N. (2010) Numerical Solution of Stochastic Differential Equations with Jumps in Finance. Springer-Verlag, Berlin and Heidelberg. https://doi.org/10.1007/978-3-642-13694-8
[33]	Wong, R. (2001) Asymptotic Approximations of Integrals. SIAM 34, Philadelphia, PA. https://doi.org/10.1137/1.9780898719260
[34]	Arnold, L. (1974) Stochastic Differential Equations: Theory and Applications. John Wiley & Sons, New York.
[35]	Klobner, F.C. (2005) Introduction to Stochastic Calculus with Applications. 2nd edition, Imperial College Press, London.
[36]	Ikeda, N. and Watanabe, S. (1989) Stochastic Differential Equations and Diffusion Processes. 2 Edition, North-Holland Publishing Company, Kodansha Scientific Books, New York.
[37]	Capasso, V. and Barstein, D. (2005) An Introduction to Continuous—Time Stochastic Processes. Birkhauser, Boston, MA.
[38]	Itô, K. and McKean Jr., H.P. (1996) Diffusion Processus and Their Sample Paths. Springer-Verlag, Berlin and Heidelberg. https://doi.org/10.1007/978-3-642-62025-6
[39]	Hu, Y.Z. and Meyer, P.A. (1993) On the Approximation of Multiple Stratonovich Integrals. In: Stochastic Processes: A Festschrift in Honour of Gopinath Kallianpur, Springer-Verlag, Inc., New York, 141-148. https://doi.org/10.1007/978-1-4615-7909-0_17
[40]	Kushner, H.J. (1984) Approximation and Weak Convergence Methods for Random Processes with Applications to Stochastic Systems Theory. The MIT Press, Cambridge, MA.
[41]	Di Nunno, G., Oksendal, B. and Proske, F. (2009) Malliavin Calculus for Lévy Processes with Applications to Finance. Springer, Berlin. https://doi.org/10.1007/978-3-540-78572-9
[42]	Malliavin, P. (1997) Stochastic Analysis. Springer-Verlag, Berlin and Heidelberg.
[43]	Friedman, A. (1975) Stochastic Differential Equations and Applications. Academic Press, New York. https://doi.org/10.1016/B978-0-12-268201-8.50010-4
[44]	Gawarecki, L. and Mandrekar, V. (2011) Stochastic Differential Equations in Infinite Dimensions with Applications to Stochastic Partial Differential Equations. Springer Verlag, Berlin and Heidelberg. https://doi.org/10.1007/978-3-642-16194-0
[45]	Kushner, H.J. and Dupuis, P. (2001) Numerical Methods for Stochastic Control Problems in Continuous Time. Springer-Verlag, New York. https://doi.org/10.1007/978-1-4613-0007-6
[46]	Malliavin, P. and Thalmaien, A. (2006) Stochastic Calculus of Variations in Mathematical Finance. Springer Finance, Berlin and Heidelberg.
[47]	Mao, X.R. (2010) Stochastic Differential Equations and Applications. 2nd Edition, Woodhead Publishing, Philadelphia, PA.
[48]	Oksendal, B. (2000) Stochastic Differential Equations. 5th Edition, Springer-Verlag, Berlin.
[49]	Mao, X.R. and Yuan, C.G. (2005) Numerical Method for Stationary Distribution of Stochastic Differential Equations with Markovian Switching. Journal of Computational and Applied Mathematics, 174, 1-27. https://doi.org/10.1016/j.cam.2004.03.016
[50]	Malliavin, P., Airault, H., Kay, L. and Letac, G. (1995) Integration and Probability. Springer Verlag, New York.
[51]	Nualart, D. (2006) Malliavin Calculus and Related Topics. Springer-Verlag, Berlin and Heidelberg.
[52]	Da Prato, G. and Zabczyk (2004) Second Order Partial Differential Equations in Hilbert Spaces. Number 293 in Lecture Notes Series. Cambridge University Press, Cambridge.
[53]	Da Prato, G. and Tubaro, L. (2002) Stochastic Partial Differential Equations and Applications. Marcel Dekker, New York. https://doi.org/10.1201/9780203910177
[54]	Da Prato, G. and Tubaro, L. (2006) Stochastic Differential Equations and Applications-VII, Volume 245 of Lecture Note in Pure and Applied Mathematics. Chapman and Hall/CRC, Boca Raton, FL. https://doi.org/10.1201/9781420028720
[55]	Ashyralyev, A. (2008) On Modified Crank-Nicholson Difference Scheme for Parabolic Equation. Numerical Functional Analysis and Optimization, 29, 268-282. https://doi.org/10.1080/01630560801998138
[56]	Kushner, H.J. and Yin, G.G. (2003) Stochastic Approximation and Recursive Algorithms and Applications. Springer-Verlag, New York.
[57]	Milstein, G.N. (1995) Numerical Integration of Stochastic Differential Equations. In: Mathematics and Its Applications Book Series, MAIA, Vol. 313, Springer Science + Business Media, Dordrecht. https://doi.org/10.1007/978-94-015-8455-5
[58]	Milstein, G.N. (1998) Numerical Integration of Stochastic Differential Equations. Springer Science + Business Media, Dordrecht.
[59]	Milstein, G.N. and Tretyakov, M.V. (2001) Numerical Solution of the Dirichlet Problem for Nonlinear Parabolic Equations by a Probabilistic Approach. IMA Journal of Numerical Analysis, 21, 887-917. https://doi.org/10.1093/imanum/21.4.887
[60]	Milstein, G.N. and Tretyakov, M.V. (2014) Numerics for Mathematical Physics. Springer, New York.
[61]	Tocino, A. and Ardanuy, R. (2002) Runge-Kutta Methods for Numerical Solution of Stochastic Differential Equations. Journal of Computational and Applied Mathematics, 138, 219-241. https://doi.org/10.1016/S0377-0427(01)00380-6
[62]	Jakobsen, N.M. and Sorensen, M. (2018) Estimating Function for Jump-Diffusions. AvaiarXiv:1709.00232v2.
[63]	Li, C. (2013) Maximum-Likelihood Estimation for Diffusion Processes via Closed Form Density Expansions. The Annals of Statistics, 41, 1350-1380. https://doi.org/10.1214/13-AOS1118
[64]	Lang, A. (2012) Mean Square Convergence of a Semidiscrete Scheme for Spdes of Zakai Type Driven by Square Integrale Martingales. Procedia Computer Science, 1, 1615-1623. https://doi.org/10.1016/j.procs.2010.04.181
[65]	Aït Sahalia, Y. (1996) Testing Continuous-Time Models of the Spot Interest Rate. Review of Financial Studies, 9, 385-426. https://doi.org/10.1093/rfs/9.2.385
[66]	Bachelier, L. (1900) Théorie de la spéculation. PhD Thesis, Ecole Normale Supérieure de Paris, Paris.
[67]	Bergomi, L. (2015) Stochastic Volatility Modeling. CRC Press, London. https://doi.org/10.1201/b19649
[68]	Merton, R.C. (1980) On Estimating the Expected Return on the Market: An Exploratory Investigation. Journal of Financial Economics, 8, 231-247. https://doi.org/10.3386/w0444
[69]	Merton, R.C. (1973) Theory of Rational Option Pricing. The Bell Journal of Econometrics and Management Science, 4, 141-183. https://doi.org/10.2307/3003143
[70]	Bollerslev, T. (1987) A Conditional Heteroskedastic Time Series Model for Speculative Prices and Rates of Return. The Review of Economics and Statistics, 69, 542-547. https://doi.org/10.2307/1925546
[71]	Nelson, D.B. and Foster, D.P. (1994) Asymptotic Filtering Theory for Univariate Arch Models. Econometrica, 62, 1-41. https://doi.org/10.2307/2951474
[72]	Klaassen, F. (2002) Improving Garch Volatility Forecasts with Regime-Switching Garch. Empirical Economics, 27, 363-394. https://doi.org/10.1007/s001810100100
[73]	Tsay, R.S. (2005) Analysis of Financial Time Series. 2nd Edition, John Wiley & Sons, Inc., Hoboken, NJ. https://doi.org/10.1002/0471746193
[74]	Box, G.E.P., Jenkins, G.M. and Reinsel, G.C. (2008) Time Series Analysis: Forecasting and Control. 4th Edition, Wiley, New York.
[75]	Engle, R.F. (1982) Autoregressive Conditional Heteroscedasticity with Estimates of the Variance of United Kingdom Inflation. Econometrica, 50, 987-1007. https://doi.org/10.2307/1912773
[76]	Hamilton, J.D. (1989) A New Approach to the Economic Analysis of Nonstationary Time Series and Business Cycle. Econometrica, 57, 357-384. https://doi.org/10.2307/1912559
[77]	Hurvich, C.M., Moulines, E. and Soulier, P. (2005) Estimating Long Memory in Volatility. Econometrica, 73, 1283-1328. https://doi.org/10.1111/j.1468-0262.2005.00616.x
[78]	Lutkepohl, H. (2005) New Introduction to Multiple Time Series Analysis. Springer-Verlag, Berlin and Heidelberg. https://doi.org/10.1007/978-3-540-27752-1
[79]	Greene, W.H. (2003) Econometric Analysis. 5th Edition, Pearson Education, Upper Saddle River, NJ.
[80]	Jensen, S.T. and Rahbek, A. (2004) Asymptotic Normality of the QMLE Estimator of Arch in the Nonstationary Case. Econometrica, 72, 641-646. https://doi.org/10.1111/j.1468-0262.2004.00504.x
[81]	Kawakatsu, H. (2007) Numerical Integration-Based Gaussian Mixture Filters for Maximum Likelihood Estimation of Asymmetric Stochastic Volatility Models. The Econometrics Journal, 10, 342-358. https://doi.org/10.1111/j.1368-423X.2007.00211.x
[82]	Mankiw, G.N. (2010) Macroeconomics. 7th Edition, Worth Publishers, New York.