The Bifurcation and Decay of Solutions for Asymptotically Linear Elliptic Systems with Parameter

Yangyang Ma

College of Science, University of Shanghai for Science and Technology, Shanghai, China.

DOI: 10.4236/jamp.2019.75083                

Abstract

This paper deals with an elliptic system of the form  where N≥3, λ is a parameter, and  is a weighted function. We employ the Rabinowitz’s global bifurcation theory and the Dancer’s unilateral global bifurcation theory to determine the existence of positive solution and negative solution on the interval of  with respect to λ. Furthermore, we also provide the decay of the positive and negative solutions.

Keywords

Elliptic System, Bifurcation Theory, Decay

Keywords:

1. Introduction

In this paper, we consider the following asymptotically linear elliptic systems

$\{\begin{array}{l}-\Delta u=\lambda p\left(x\right)f\left(u\right)\mathrm{<mi>\; </mi>\; <mi>\; </mi>}\text{in}{ℝ}^N,\\ -\Delta v=\lambda p\left(x\right)g\left(v\right)\mathrm{<mi>\; </mi>\; <mi>\; </mi>}\text{in}{ℝ}^N,\\ u,v\to \mathrm{0\; <mi>\; </mi>\; <mi>\; </mi>\; <mi>\; </mi>\; <mi>\; </mi>\; <mi>\; </mi>\; <mi>\; </mi>\; <mi>\; </mi>\; <mi>\; </mi>\; <mi>\; </mi>\; <mi>\; </mi>\; <mi>\; </mi>\; <mi>\; </mi>\; <mi>\; </mi>\; <mi>\; </mi>\; <mi>\; </mi>\; <mi>\; </mi>\; <mi>\; </mi>\; <mi>\; </mi>\; <mi>\; </mi>\; <mi>\; </mi>}\text{as}\left|x\right|\to \infty ,\end{array}$ (1.1)

where $N\ge 3$ , $\lambda$ is a parameter, and $p\left(x\right)\in C_{loc}^{\alpha }\left({ℝ}^N,ℝ\right)\left(0<\alpha <1\right)$ is a weighted function. Moreover, the nonlinear perturbations satisfy the following assumptions:

(H1) $f\mathrm{,}g\mathrm{<mo>\; :\; </mo>}ℝ\to ℝ$ are two Hölder continuous functions with exponent $\alpha$ such that $f\left(s\right)s>0,g\left(s\right)>0$ for all $s\ne 0$ ;

(H2) There exist $l_0\mathrm{,}{l}_{\infty }\in \left(\mathrm{0,}+\infty \right)$ with $l_0\ne l_{\infty }$ such that

$\underset{s\to 0}{\lim }\frac{f\left(s\right)}{s}=0=\underset{s\to 0}{\lim }\frac{g\left(s\right)}{s},\underset{s\to \infty }{\lim }\frac{f\left(s\right)}{s}=0=\underset{s\to \infty }{\lim }\frac{g\left(s\right)}{s}.$

The primary motivation for this paper comes from the study of radial entire solutions, spectrum and bifurcation for the following semi-linear elliptic problem

$\{\begin{array}{l}-\Delta u=\lambda p\left(x\right)h\left(u\right)\mathrm{<mi>\; </mi>\; <mi>\; </mi>\; <mi>\; </mi>}\text{in}{ℝ}^N,\\ u\to \mathrm{0\; <mi>\; </mi>\; <mi>\; </mi>\; <mi>\; </mi>\; <mi>\; </mi>\; <mi>\; </mi>\; <mi>\; </mi>\; <mi>\; </mi>\; <mi>\; </mi>\; <mi>\; </mi>\; <mi>\; </mi>\; <mi>\; </mi>\; <mi>\; </mi>\; <mi>\; </mi>\; <mi>\; </mi>\; <mi>\; </mi>\; <mi>\; </mi>\; <mi>\; </mi>\; <mi>\; </mi>\; <mi>\; </mi>\; <mi>\; </mi>\; <mi>\; </mi>\; <mi>\; </mi>\; <mi>\; </mi>}\text{as}\left|x\right|\to \infty ,\end{array}$ (1.2)

where $N\ge 3$ , $\lambda$ is a real parameter, and $p\left(x\right)\in C_{loc}^{\alpha }\left({ℝ}^N,ℝ\right)\left(0<\alpha <1\right)$ is a weighted or radially symmetric function.

If there exist two continuous radially symmetric functions q and Q such that

$0<q\left(\left|x\right|\right)\le Q\left(\left|x\right|\right)\text{for}\text{all}x\in {ℝ}^N$

and

${\displaystyle {\int }_{{ℝ}^N}}{\left|x\right|}^{2-N}Q\left(\left|x\right|\right)\text{d}x<+\infty ,$ (1.3)

then Edelson and Rumbos [1] have obtained that problem (1.2) is similar to the classical Laplace eigenvalue problem. Furthermore, if Q satisfies the following more strong condition

${\displaystyle {\int }_0^{+\infty }}{\rho }^{N-1}Q\left(\rho \right)\text{d}\rho <+\infty \mathrm{,}$ (1.4)

the eigenfunction $\varphi$ has the asymptotic property

$\underset{\left|x\right|\to +\infty }{\lim }{\left|x\right|}^{N-2}\varphi \left(x\right)=c$ (1.5)

for some constant c.

If $h\left(u\right)=u$ , and $p\left(x\right)$ is a radially symmetric function, $p\in C\left[\mathrm{0,}+\infty \right)\mathrm{,}p\left(s\right)\ge 0$ on $\left[\mathrm{0,}+\infty \right)$ , and $p\left(s\right)\cancel{\equiv }0$ on $\left[T\mathrm{,}+\infty \right)$ . The further condition

${\displaystyle {\int }_0^{+\infty }}\rho p\left(\rho \right)\text{d}\rho <+\infty$ (1.6)

and

${\displaystyle {\int }_0^{+\infty }}{\rho }^{N-1}p\left(\rho \right)\text{d}\rho <+\infty \mathrm{,}$ (1.7)

Naito [2] has the following results:

1) Under the assumption (1.6), the number of zeros of every nontrivial radial entire solution near the first eigenvalue.

2) Under the assumption (1.7), the number of zeros of every nontrivial radial entire solution near higher order eigenvalue.

2. Preliminaries and Results

In this section, we will give some lemmas and our results.

Suppose that $Q\left(x\right)\in C\left({ℝ}^N\mathrm{,}ℝ\right)$ is a positive radially symmetric function satisfying (1.3). Denote by $S\left({ℝ}^N\right)$ the set of all measurable real functions defined on ${ℝ}^N$ . Let $L^2\left({ℝ}^N,Q\left(x\right)\right):=\left\{u\in S\left({ℝ}^N\right):{\displaystyle {\int }_{{ℝ}^N}}Q\left(x\right)u^2\left(x\right)\text{d}x<+\infty \right\}$ . The set $L^2\left({ℝ}^N\mathrm{,}Q\left(x\right)\right)$ together with the inner product

${\left(u,v\right)}_Q={\displaystyle {\int }_{{ℝ}^N}}Q\left(x\right)u\left(x\right)v\left(x\right)\text{d}x\text{for}\text{all}u,v\in L^2\left({ℝ}^N,Q\left(x\right)\right).$ (2.1)

For $N\ge 3$ and $2^{\ast }=\frac{2N}{N-2}$ , defining

$D^{1,2}\left({ℝ}^N\right):=\left\{u\in L^{2^{\ast }}\left({ℝ}^N\right):\left|\nabla u\right|\in L^2\left({ℝ}^N\right)\right\},$ (2.2)

endowed with the norm ${\Vert u\Vert }_1={\left({\displaystyle {\int }_{{ℝ}^{\mathbb{N}}}}{\left|\nabla u\right|}^2\right)}^{\frac{1}{2}}$ .

Define

$M\left(\Omega \right):=\left\{p\left(x\right)\in C_{loc}^{\alpha }\left(\Omega ,ℝ\right):\left\{x\in \Omega :p\left(x\right)>0\right\}\ne \varnothing \right\},$ (2.3)

where $\Omega \subseteq {ℝ}^N$ .

Next, we will define our work space

$X=\left\{u\in C\left({ℝ}^N,{ℝ}^N\right):\underset{x\in {ℝ}^N}{\sup }\left|u\left(x\right)\right|<+\infty \right\},$ (2.4)

with the norm

$\Vert u\Vert =\underset{{ℝ}^N}{\sup }\left|u\left(x\right)\right|\text{for}x\in X\mathrm{.}$

Now we consider the following boundary value problem

$\{\begin{array}{l}-\Delta u=\lambda p\left(x\right)u\mathrm{<mi>\; </mi>\; <mi>\; </mi>\; <mi>\; </mi>}\text{in}{ℝ}^N,\\ u\to \mathrm{0\; <mi>\; </mi>\; <mi>\; </mi>\; <mi>\; </mi>\; <mi>\; </mi>\; <mi>\; </mi>\; <mi>\; </mi>\; <mi>\; </mi>\; <mi>\; </mi>\; <mi>\; </mi>\; <mi>\; </mi>\; <mi>\; </mi>\; <mi>\; </mi>\; <mi>\; </mi>\; <mi>\; </mi>\; <mi>\; </mi>\; <mi>\; </mi>\; <mi>\; </mi>}\text{as}\left|x\right|\to \infty ,\end{array}$ (2.5)

where $\lambda$ is parameter, $p\left(x\right)\in M\left({ℝ}^N\right)$ .

Lemma 2.1 ( [3] ) Assume that $Q\in C\left({ℝ}^N\mathrm{,}ℝ\right)$ is positive, radially symmetric function and satisfies (1.3), and $p\left(x\right)\in M\left({ℝ}^N\right)$ such that $\left|p\left(x\right)\right|\le Q\left(\left|x\right|\right)$ for all $x\in {ℝ}^N$ . Then there exists an orthogonal basis ${\left\{{\phi }_k\right\}}_1^{+\infty }$ of $L^2\left({ℝ}^N\mathrm{,}\left|p\left(x\right)\right|\right)$ and a sequence of positive real numbers ${\left\{{\eta }_k\right\}}_1^{+\infty }$ with ${\eta }_k\to +\infty$ as $k\to +\infty$ such that problem (2.5) satisfying

$0<{\eta }_1\le {\eta }_2\le \cdots \le {\eta }_k\le \cdots ,$

$\{\begin{array}{l}-\Delta {\phi }_k={\eta }_{k}p\left(x\right){\phi }_k\mathrm{<mi>\; </mi>\; <mi>\; </mi>\; <mi>\; </mi>\; <mi>\; </mi>\; <mi>\; </mi>}\text{in}{ℝ}^N,\\ {\phi }_k\in D^{1,2}\left({ℝ}^N\right)\cap C_{loc}^{2+\alpha }\left({ℝ}^N,ℝ\right),\\ {\phi }_k\to \mathrm{0\; <mi>\; </mi>\; <mi>\; </mi>\; <mi>\; </mi>\; <mi>\; </mi>\; <mi>\; </mi>\; <mi>\; </mi>\; <mi>\; </mi>\; <mi>\; </mi>\; <mi>\; </mi>\; <mi>\; </mi>\; <mi>\; </mi>}\text{as}\left|x\right|\to +\infty .\end{array}$ (2.6)

Before giving the Lemma 2.2, it is necessary to give the definition of a nodal domain. For the function $u$ defining on the ${ℝ}^N$ , we say that a nodal domain of $u$ is connected component of ${ℝ}^N\backslash \left\{x\in {ℝ}^N:u\left(x\right)=0\right\}$ .

Lemma 2.2 ( [3] ) Assume that $p\left(x\right)\ge 0$ and satisfies the assumptions of Lemma 2.1. Let $\phi$ be any eigenfunction associated to an eigenvalue $\eta$ and $\mathcal{N}$ be its any nodal domain. Then we have

$\left|\mathcal{N}\right|\ge c\mathrm{,}$ (2.7)

where $c>0$ is some constant depending only on N and $\eta$ .

Lemma 2.3 Assume that there exists a positive constant ${\rho }_1>0$ such that

$\frac{f\left(s\right)}{s}\ge {\rho }_1\mathrm{,}\frac{g\left(s\right)}{s}\ge {\rho }_1$ (2.8)

for any $s\ne 0$ . Then there exists ${\sigma }_1>0$ such that problem (1.1) has no one-sign solution for any $\lambda >{\sigma }_1$ .

Proof. Let $\left(\tilde{u},\tilde{v}\right)$ be positive solution of problem (1.1). By Lemma 2.1, we have

$\{\begin{array}{l}-\Delta {\phi }_1={\eta }_{1}p\left(x\right){\phi }_1\mathrm{<mi>\; </mi>\; <mi>\; </mi>\; <mi>\; </mi>}\text{in}{ℝ}^N,\\ {\phi }_1\to \mathrm{0\; <mi>\; </mi>\; <mi>\; </mi>\; <mi>\; </mi>\; <mi>\; </mi>\; <mi>\; </mi>\; <mi>\; </mi>}\text{as}\left|x\right|\to \infty .\end{array}$ (2.9)

Multiplying (2.9) by $\tilde{u}$ , we get

${\displaystyle {\int }_{{ℝ}^N}}\nabla \tilde{u}\nabla {\phi }_1\text{d}x={\eta }_1{\displaystyle {\int }_{{ℝ}^N}}p\left(x\right)\tilde{u}{\phi }_1\text{d}x.$ (2.10)

Multiplying the first equation of (1.1) by ${\phi }_1$ , we have

${\displaystyle {\int }_{{ℝ}^N}}\nabla \tilde{u}\nabla {\phi }_1\text{d}x=\lambda {\displaystyle {\int }_{{ℝ}^N}}p\left(x\right)f\left(\tilde{v}\right){\phi }_1\text{d}x.$ (2.11)

This yields

$\begin{array}{c}{\eta }_1{\displaystyle {\int }_{{ℝ}^N}}p\left(x\right)\tilde{u}{\phi }_1\text{d}x=\lambda {\displaystyle {\int }_{{ℝ}^N}}p\left(x\right)f\left(\tilde{v}\right){\phi }_1\text{d}x\\ =\lambda {\displaystyle {\int }_{{ℝ}^N}}p\left(x\right)\frac{f\left(\tilde{v}\right)}{\tilde{v}}\tilde{v}{\phi }_1\text{d}x\\ \ge \lambda {\rho }_1{\displaystyle {\int }_{{ℝ}^N}}p\left(x\right)\tilde{v}{\phi }_1\text{d}x.\end{array}$ (2.12)

Similarly, we have

$\begin{array}{c}{\eta }_1{\displaystyle {\int }_{{ℝ}^N}}p\left(x\right)\tilde{v}{\phi }_1\text{d}x=\lambda {\displaystyle {\int }_{{ℝ}^N}}p\left(x\right)g\left(\tilde{u}\right){\phi }_1\text{d}x\\ =\lambda {\displaystyle {\int }_{{ℝ}^N}}p\left(x\right)\frac{g\left(\tilde{u}\right)}{\tilde{u}}\tilde{u}{\phi }_1\text{d}x\\ \ge \lambda {\rho }_1{\displaystyle {\int }_{{ℝ}^N}}p\left(x\right)\tilde{u}{\phi }_1\text{d}x.\end{array}$ (2.13)

Thus it follow that $0<\lambda \le \frac{{\eta }_1}{{\rho }_1}$ . Therefore, the proof of lemma 2.3 is completed. □

Lemma 2.4 Assume that there exists a positive constant ${\rho }_2>0$ such that

$\frac{f\left(s\right)}{s}\le {\rho }_2\mathrm{,}\frac{g\left(s\right)}{s}\le {\rho }_2$ (2.14)

for any $s\ne 0$ . Then there exists ${\sigma }_2>0$ such that problem (1.1) has no one-sign solution for any $0<\lambda <{\sigma }_2$ . □

Proof. The proof follows similarly with minor changes.

Following lemmas will be helpful in the sequel.

Lemma 2.5 (Lebesgue dominanted convergence) Let $\Omega \subset {ℝ}^N$ be open and let $u_k\left(x\right)\subset L^1\left(\Omega \right)$ be a sequence such that

1) $u_k\left(x\right)\to u\left(x\right)$ a.e. in $\Omega$ as $k\to +\infty$ ,

2) there exists $U\left(x\right)\in L^1\left(\Omega \right)$ such that for all k, $\left|u_k\left(x\right)\right|\le U\left(x\right)$ a.e. in $\Omega$ .

Then $u\in L^1\left(\Omega \right)$ and $u_k\to u$ in the $L^1\left(\Omega \right)$ norm, namely $u\in {\displaystyle {\int }_{\Omega }}\left|u_k-u\right|\text{d}x\to 0$ as $k\to +\infty$ .

Lemma 2.6 (Strong maximum principle) Let the operator L is uniformly elliptic in $\Omega$ (may not be bounded), $c=0$ and $Lu\ge 0\left(\le 0\right)$ . Then, if the maximum (minimum) of u can be assumed in the interior of $\Omega$ , then u is a

constant; if $c\le 0$ and $\frac{c}{\lambda }$ is bounded, then the nonnegative maximum

(non-positive minimum) of u can’t be assumed in the interior of $\Omega$ unless u is a constant.

Now we state our main results.

Theorem 2.1 Let the assumptions of Lemma 1 hold. If $p\left(x\right)\ge 0$ and (H1), (H2) are satisfied. Then for any

$\lambda \in \left(\min \left\{\frac{{\eta }_1}{l_0}\mathrm{,}\frac{{\eta }_1}{l_{\infty }}\right\}\mathrm{,}\max \left\{\frac{{\eta }_1}{l_0}\mathrm{,}\frac{{\eta }_1}{l_{\infty }}\right\}\right)\mathrm{,}$

problem (1.1) admit at least two one-sign solutions $\left(u^{+}\mathrm{,}{v}^{+}\right)$ and $\left(u^{-}\mathrm{,}{v}^{-}\right)$ such that $\left(u^{+},v^{+}\right)>0$ and $\left(u^{-},v^{-}\right)<0$ in ${ℝ}^N$ .

Theorem 2.2 Assume that 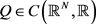is positive, radially symmetric function and satisfies (1.4), and $p\left(x\right)\in M\left({ℝ}^N\right)$ such that $0\le p\left(x\right)\le Q\left(\left|x\right|\right)$ for all $x\in {ℝ}^N$ . If $\left(u^{+}\mathrm{,}{v}^{+}\right)$ and $\left(u^{-}\mathrm{,}{v}^{-}\right)$ are given in Theorem 2.1. Then there exist constants $c_1,c_2>0$ and $c_3,c_4<0$ such that

$\underset{\left|x\right|\to +\infty }{\lim }{\left|x\right|}^{N-2}{u}^{+}=c_1,\underset{\left|x\right|\to +\infty }{\lim }{\left|x\right|}^{N-2}{v}^{+}=c_2$ (2.15)

and

$\underset{\left|x\right|\to +\infty }{\lim }{\left|x\right|}^{N-2}{u}^{-}=c_3,\underset{\left|x\right|\to +\infty }{\lim }{\left|x\right|}^{N-2}{v}^{-}=c_4.$ (2.16)

3. Proofs of Main Results

Define the integral operator

$T\left(u\right)=-{\displaystyle {\int }_{{ℝ}^N}}\Gamma \left(x-y\right)p\left(y\right)u\left(y\right)\text{d}y\mathrm{,}$ (3.1)

where $\Gamma \left(x-y\right)=\frac{1}{N\left(2-N\right){\omega }_N}{\left|x-y\right|}^{2-N}$ , ${\omega }_N$ denotes the volume of the unit ball in ${ℝ}^N$ .

Eedlson [4] has showed that $T\mathrm{<mo>\; :\; </mo>}X\to X$ is linear, continuous and compact.

Lemma 3.1 $\left(u\mathrm{,}v\right)$ is one-sign $C^{2+\alpha }\left({ℝ}^N\right)$ solution of problem (1.1) $\iff$ $\left(u\mathrm{,}v\right)$ solves the following operator equations

$\{\begin{array}{l}u=\lambda T\left(f\left(v\right)\right)\mathrm{<mi>\; </mi>\; <mi>\; </mi>}\text{in}{ℝ}^N,\\ v=\lambda T\left(g\left(u\right)\right)\mathrm{<mi>\; </mi>\; <mi>\; </mi>}\text{in}{ℝ}^N,\\ u,v\to \mathrm{0\; <mi>\; </mi>\; <mi>\; </mi>\; <mi>\; </mi>\; <mi>\; </mi>\; <mi>\; </mi>\; <mi>\; </mi>\; <mi>\; </mi>\; <mi>\; </mi>\; <mi>\; </mi>}\mathrm{<mi>\; </mi>\; <mi>\; </mi>\; <mi>\; </mi>}\text{as}\left|x\right|\to +\infty \end{array}$ (3.2)

in $X^2$ .

Proof. “ $\Rightarrow$ ”

Let $\left(\hat{u},\hat{v}\right)$ is a one-sign $C^{2+\alpha }\left({ℝ}^N\right)$ solution of problem (1.1), if necessary, we assume $\left(\hat{u},\hat{v}\right)>0$ .

For $r>0$ , we consider the following boundary value problem

$\{\begin{array}{l}-\Delta u=\lambda p\left(x\right)f\left(\hat{v}\right)\mathrm{<mi>\; </mi>\; <mi>\; </mi>\; <mi>\; </mi>\; <mi>\; </mi>\; <mi>\; </mi>}x\in B_r,\\ u=\psi \left(x\right)>\mathrm{0\; <mi>\; </mi>\; <mi>\; </mi>\; <mi>\; </mi>\; <mi>\; </mi>\; <mi>\; </mi>\; <mi>\; </mi>\; <mi>\; </mi>\; <mi>\; </mi>\; <mi>\; </mi>\; <mi>\; </mi>}\mathrm{<mi>\; </mi>\; <mi>\; </mi>\; <mi>\; </mi>\; <mi>\; </mi>}x\in \partial B_r,\end{array}$ (3.3)

where $B_r$ is a ball of radius of r in ${ℝ}^N$ , $\psi \left(x\right)\in D^{\mathrm{1,2}}\left({ℝ}^N\right)\cap C^1\left({ℝ}^N\mathrm{,}ℝ\right)$ .

For $\hat{u}\in C^{2+\alpha }\left({ℝ}^N\right)$ , problem (3.3) has the unique fundamental solution $u_r$ , expressed as

$u_r=-\lambda {\displaystyle {\int }_{B_r}}{G}_r\left(x,y\right)p\left(y\right)f\left(\hat{v}\left(y\right)\right)\text{d}y+\frac{r^2-{\left|x\right|}^2}{N{\omega }_{N}r}{\displaystyle {\int }_{\left|x\right|=r}}\frac{\psi \left(y\right)}{{\left|x-y\right|}^N}\text{d}{S}_y,$ (3.4)

where

$G_r\left(x,y\right)=\{\begin{array}{l}\Gamma \left(\left|x-y\right|\right)-\Gamma \left(\frac{\left|y\right|}{r}\left|x-\bar{y}\right|\right)\mathrm{<mi>\; </mi>\; <mi>\; </mi>\; <mi>\; </mi>\; <mi>\; </mi>}y\ne 0\hfill \\ \Gamma \left(\left|x\right|\right)-\Gamma \left(r\right)\mathrm{<mi>\; </mi>\; <mi>\; </mi>\; <mi>\; </mi>\; <mi>\; </mi>\; <mi>\; </mi>\; <mi>\; </mi>\; <mi>\; </mi>\; <mi>\; </mi>\; <mi>\; </mi>\; <mi>\; </mi>\; <mi>\; </mi>\; <mi>\; </mi>\; <mi>\; </mi>\; <mi>\; </mi>\; <mi>\; </mi>\; <mi>\; </mi>\; <mi>\; </mi>\; <mi>\; </mi>\; <mi>\; </mi>\; <mi>\; </mi>\; <mi>\; </mi>\; <mi>\; </mi>\; <mi>\; </mi>}y=0\hfill \end{array},\mathrm{<mi>\; </mi>}\bar{y}=\left(r^2/{\left|y\right|}^2\right)y\mathrm{<mi>\; </mi>}\left(y\ne 0\right).$ (3.5)

Fix $x\in {ℝ}^N$ and choose $r>0$ so large such that $r>2\left|x\right|$ , then

$\begin{array}{c}{\displaystyle {\int }_{\left|y\right|=r}}\frac{\psi \left(y\right)}{{\left|x-y\right|}^N}\text{d}{S}_y=\frac{1}{r^N}{\displaystyle {\int }_{\left|y\right|=r}}\frac{\psi \left(y\right)}{{\left|\frac{x}{r}-\frac{y}{r}\right|}^N}\text{d}{S}_y\\ =\frac{1}{r}{\displaystyle {\int }_{\left|y\right|=1}}\frac{\psi \left(r\omega \right)}{{\left|x/r-\omega \right|}^N}\text{d}{S}_{\omega }\\ <\frac{2^N}{r}{\displaystyle {\int }_{\left|\omega \right|=1}}\psi \left(r\omega \right)\text{d}{S}_{\omega },\end{array}$ (3.6)

so that

$\frac{r^2-{\left|x\right|}^2}{N{\omega }_{N}r}{\displaystyle {\int }_{\left|y\right|=r}}\frac{\psi \left(y\right)}{{\left|x-y\right|}^N}\text{d}{S}_y<2^N\left(1-\frac{{\left|x\right|}^2}{r^2}\right)\frac{1}{N{\omega }_N}{\displaystyle {\int }_{\left|\omega \right|=1}}\psi \left(r\omega \right)\text{d}{S}_{\omega }.$ (3.7)

Setting $\bar{\psi }\left(r\omega \right)=\frac{1}{N{\omega }_N}{\displaystyle {\int }_{\left|\omega \right|=1}}\psi \left(r\omega \right)\text{d}{S}_{\omega }$ , we shall show that $\bar{\psi }\left(r\omega \right)\to \mathrm{0\; <mi>\; </mi>}\left(r\to +\infty \right)$ .

Writing $\left(r\mathrm{,}\omega \right)$ for polar coordinates in ${ℝ}^N$ , we have

$\begin{array}{c}\psi \left(r\omega \right)=\psi \left(r,\omega \right)\\ =-{\displaystyle {\int }_r^{+\infty }}\frac{\partial \psi }{\partial t}\left(t,\omega \right)\text{d}t\\ <-{\displaystyle {\int }_r^{+\infty }}{t}^{\frac{1-N}{2}}{t}^{\frac{N-1}{2}}\frac{\partial \psi }{\partial t}\left(t,\omega \right)\text{d}t.\end{array}$ (3.8)

The Cauchy-Schwartz inequality implies

$\begin{array}{c}{\left|\psi \left(r\mathrm{,}\omega \right)\right|}^2=\frac{r^{2-N}}{N-2}{\displaystyle {\int }_r^{+\infty }}{t}^{N-1}{\left|\frac{\partial \psi }{\partial t}\left(t\mathrm{,}\omega \right)\right|}^2\text{d}t\\ \le \frac{r^{2-N}}{N-2}{\displaystyle {\int }_r^{+\infty }}{t}^{N-1}{\left|\nabla \psi \left(t\mathrm{,}\omega \right)\right|}^2\text{d}t\mathrm{.}\end{array}$ (3.9)

So that

${\left|\psi \left(r\mathrm{,}\omega \right)\right|}^2\le \frac{r^{2-N}}{N-2}{\displaystyle {\int }_0^{+\infty }}{t}^{N-1}{\left|\nabla \psi \left(t\mathrm{,}\omega \right)\right|}^2\text{d}t\mathrm{.}$ (3.10)

From (3.10) one gets

$\left|\psi \left(r\mathrm{,}\omega \right)\right|\le \frac{r^{\frac{2-N}{2}}}{\sqrt{N-2}}{\left({\displaystyle {\int }_0^{+\infty }}{t}^{N-1}{\left|\nabla \psi \left(t\mathrm{,}\omega \right)\right|}^2\text{d}t\right)}^{\frac{1}{2}}\mathrm{.}$ (3.11)

Integrating on both sides over the unit sphere in ${ℝ}^N$ we obtain

${\displaystyle {\int }_{\left|\omega \right|=1}}\left|\psi \left(r\mathrm{,}\omega \right)\right|\text{d}{S}_{\omega }\le \frac{r^{\frac{2-N}{2}}}{\sqrt{N-2}}{\displaystyle {\int }_{\left|\omega \right|=1}}{\left({\displaystyle {\int }_0^{+\infty }}{t}^{N-1}{\left|\nabla \psi \left(t\mathrm{,}\omega \right)\right|}^2\text{d}t\right)}^{\frac{1}{2}}\text{d}{S}_{\omega }\mathrm{.}$ (3.12)

An application of the Cauchy-Schwartz inequality then yields

${\displaystyle {\int }_{\left|\omega \right|=1}}\left|\psi \left(r\mathrm{,}\omega \right)\right|\text{d}{S}_{\omega }\le \frac{r^{\frac{2-N}{2}}}{\sqrt{N-2}}\sqrt{N{\omega }_N}{\left({\displaystyle {\int }_{{ℝ}^N}}{\left|\nabla \psi \left(t\mathrm{,}\omega \right)\right|}^2\text{d}x\right)}^{\frac{1}{2}}\mathrm{.}$ (3.13)

By (3.13), we have

$\frac{1}{N{\omega }_N}{\displaystyle {\int }_{\left|\omega \right|=1}}\left|\psi \left(r\mathrm{,}\omega \right)\right|\text{d}{S}_{\omega }\le \frac{r^{\frac{2-N}{2}}}{\sqrt{N\left(N-2\right){\omega }_N}}{\Vert \psi \left(x\right)\Vert }_1\mathrm{.}$ (3.14)

Thus we obtain

$\bar{\psi }\left(r\omega \right)\le \frac{r^{\frac{2-N}{2}}}{\sqrt{N\left(N-2\right){\omega }_N}}{\Vert \psi \left(x\right)\Vert }_1\to \mathrm{0\; <mi>\; </mi>}\left(r\to +\infty \right)\mathrm{.}$ (3.15)

Hence, by the previous equality, one get

$\frac{r^2-{\left|x\right|}^2}{N{\omega }_{N}r}{\displaystyle {\int }_{\left|x\right|=r}}\frac{\psi \left(y\right)}{{\left|x-y\right|}^N}\text{d}{S}_y\to 0\text{as}r\to +\infty .$ (3.16)

Next, we still show that for any $x\ne y$ , $G_r\left(x\mathrm{,}y\right)\to \Gamma \left(x-y\right)$ as $r\to +\infty$ .

For $r>0$ , we have

$0\le -G_r\left(x-y\right)=\left|\Gamma \left(x-y\right)\right|-\left|\Gamma \left(\frac{\left|y\right|}{r}x-\bar{y}\right)\right|\le \left|\Gamma \left(x-y\right)\right|.$ (3.17)

Note that (H1) and (H2), there exists a constant $c>0$ such that ${\sup }_{x\in {ℝ}^N}c\left|a\left(\hat{v}\right)\right|\le 1$ . For our convenience, $c\left|a\left(\hat{v}\right)\right|$ is denoted by $\left|a\left(\hat{v}\right)\right|$ . Since $\Gamma \left(x-y\right)$ is harmonic with respect to $y$ , we have

$\begin{array}{l}{\displaystyle {\int }_{B_r}}\left|\Gamma \left(x-y\right)\right|p\left(y\right)f\left(\hat{v}\left(y\right)\right)\text{d}y\\ \le {\displaystyle {\int }_{B_r}}\left|\Gamma \left(x-y\right)\right|Q\left(y\right)\text{d}y=\frac{1}{N-2}{\displaystyle {\int }_0^r}{\left|x\right|}^{2-N}{\rho }^{N-1}Q\left(\rho \right)\text{d}\rho \\ =\frac{1}{N-2}\left({\displaystyle {\int }_0^{\left|x\right|}}{\left|x\right|}^{2-N}{\rho }^{N-1}Q\left(\rho \right)\text{d}\rho +{\displaystyle {\int }_{\left|x\right|}^r}{\left|x\right|}^{2-N}{\rho }^{N-1}Q\left(\rho \right)\text{d}\rho \right)\\ \le \frac{1}{N-2}\left({\displaystyle {\int }_0^{\left|x\right|}}\rho Q\left(\rho \right)\text{d}\rho +{\displaystyle {\int }_{\left|x\right|}^r}\rho Q\left(\rho \right)\text{d}\rho \right)\\ =\frac{1}{N-2}\left({\displaystyle {\int }_0^r}\rho Q\left(\rho \right)\text{d}\rho \right)=\frac{1}{N-2}\left({\displaystyle {\int }_0^{+\infty }}\rho Q\left(\rho \right)\text{d}\rho \right)<+\infty .\end{array}$ (3.18)

By Lebesgue Dominated Convergence Theorem,

$-{\displaystyle {\int }_{B_r}}{G}_r\left(x\mathrm{,}y\right)p\left(y\right)f\left(\hat{v}\left(y\right)\right)\text{d}y\to -{\displaystyle {\int }_{{ℝ}^N}}\Gamma \left(x-y\right)p\left(y\right)f\left(\hat{v}\left(y\right)\right)\text{d}y.$ (3.19)

as $r\to +\infty$ , and for $\hat{v}\in C^{2+\alpha }\left({ℝ}^N\right)$ , using (3.13)-(3.19), we obtain

$u=-\lambda {\displaystyle {\int }_{B_r}}\Gamma \left(x-y\right)p\left(y\right)f\left(\hat{v}\left(y\right)\right)\text{d}y\mathrm{.}$ (3.20)

By the uniqueness of the solution to problem (1.1), we have $\hat{u}=u$ , that is,

$\hat{u}=-\lambda {\displaystyle {\int }_{B_r}}\Gamma \left(x-y\right)p\left(y\right)f\left(\hat{v}\left(y\right)\right)\text{d}y.$ (3.21)

By similarly, for $\hat{u}\in C^{2+\alpha }\left({ℝ}^N\right)$ , we get

$\hat{v}=-\lambda {\displaystyle {\int }_{B_r}}\Gamma \left(x-y\right)p\left(y\right)f\left(\hat{u}\left(y\right)\right)\text{d}y.$ (3.22)

Therefore, $\left(\hat{u}\mathrm{,}\hat{v}\right)$ satisfies the following operator equations

$\begin{array}{l}\{\begin{array}{l}u=\lambda T\left(f\left(v\right)\right)\mathrm{<mi>\; </mi>\; <mi>\; </mi>}\text{in}{ℝ}^N,\\ v=\lambda T\left(g\left(u\right)\right)\mathrm{<mi>\; </mi>\; <mi>\; </mi>\; <mi>\; </mi>}\text{in}{ℝ}^N,\\ u,v\to \mathrm{0\; <mi>\; </mi>\; <mi>\; </mi>\; <mi>\; </mi>\; <mi>\; </mi>\; <mi>\; </mi>\; <mi>\; </mi>\; <mi>\; </mi>\; <mi>\; </mi>\; <mi>\; </mi>\; <mi>\; </mi>\; <mi>\; </mi>}\mathrm{<mi>\; </mi>}\text{as}\left|x\right|\to +\infty .\end{array}\hfill \end{array}$ (3.23)

“ $\Leftarrow$ ” The proofs of this part are analogous to the processes of [4] . □

Lemma 3.2 The solutions of problem (3.2) are acquired by the following equation

$\{\begin{array}{l}u=\lambda T\left(f\left(\lambda Tg\left(u\right)\right)\right)x\in {ℝ}^N,\\ u\to \mathrm{0\; <mi>\; </mi>\; <mi>\; </mi>\; <mi>\; </mi>\; <mi>\; </mi>\; <mi>\; </mi>\; <mi>\; </mi>\; <mi>\; </mi>\; <mi>\; </mi>\; <mi>\; </mi>\; <mi>\; </mi>\; <mi>\; </mi>\; <mi>\; </mi>\; <mi>\; </mi>\; <mi>\; </mi>\; <mi>\; </mi>\; <mi>\; </mi>\; <mi>\; </mi>\; <mi>\; </mi>\; <mi>\; </mi>\; <mi>\; </mi>\; <mi>\; </mi>\; <mi>\; </mi>\; <mi>\; </mi>\; <mi>\; </mi>\; <mi>\; </mi>\; <mi>\; </mi>}\text{as}\left|x\right|\to +\infty .\end{array}$ (3.24)

Proof. Let $\bar{u}$ is the solution of problem (3.24), then we have

$\bar{v}=\lambda T\left(g\left(\bar{u}\right)\right).$ (3.25)

thus $\bar{u}=\lambda T\left(f\left(\lambda Tg\left(\bar{u}\right)\right)\right)=\lambda Tf\left(\bar{v}\right)$ , that is, $\left(\bar{u}\mathrm{,}\bar{v}\right)$ solves the Equations (3.2).

Next, we will show that $\bar{v}\to 0$ as $\left|x\right|\to +\infty$ . By (H2), we have $g\left(s\right)=l_{0}s+o\left(s\right)$ , and $\bar{v}\to 0$ as $\left|x\right|\to +\infty$ . Hence, we obtain $g\left(\bar{u}\right)\to 0$ as $\left|x\right|\to +\infty$ .

Since the operator T is linear, continuous and compact, $\bar{v}\to 0$ as $\left|x\right|\to +\infty$ . □

Proof of Theorem 2.1. From the previous processes, we know that $T\mathrm{<mo>\; :\; </mo>}X\to X$ is linear, continuous and compact. By Lemma 3.2, we have that the solutions to problem (3.2) can be determined by $u=\lambda T\left(f\left(\lambda Tg\left(u\right)\right)\right)$ .

Define

$\Sigma :={\overline{\left\{\left(\lambda ,u\right):u=\lambda T\left(f\left(\lambda Tg\left(u\right)\right)\right)\text{and}u\ne 0\right\}}}^{ℝ\times X}.$ (3.26)

Let $P^{+}:=\left\{u\in X:u\left(x\right)>0\text{for}x\in {ℝ}^N\right\}$ and $P^{-}:=\left\{u\in X:u\left(x\right)<0\text{for}x\in {ℝ}^N\right\}$ .

Suppose that ${\xi }_1\mathrm{,}{\xi }_2\mathrm{<mo>\; :\; </mo>}ℝ\to ℝ$ such that $f\left(s\right)=l_{0}s+{\xi }_1\left(s\right),\mathrm{<mi>\; </mi>}g\left(s\right)=l_{0}s+{\xi }_2\left(s\right)$ with

$\underset{s\to 0}{\lim }\frac{{\xi }_1\left(s\right)}{s}=0=\underset{s\to 0}{\lim }\frac{{\xi }_2\left(s\right)}{s}.$ (3.27)

Thus we have

$u={\lambda }^2{l}_0^2{T}^{2}u+{\lambda }^2{l}_0{T}^2{\xi }_2\left(u\right)+\lambda T{\xi }_1\left(\lambda l_{0}Tu+{\xi }_2\left(u\right)\right).$ (3.28)

Set ${\lambda }^2=\mu ,\mathrm{<mi>\; </mi>}{l}_0^2{T}^2=A,\mathrm{<mi>\; </mi>}{\lambda }^2{l}_0{T}^2{\xi }_2\left(u\right)+\lambda T{\xi }_1\left(\lambda l_{0}Tu+{\xi }_2\left(u\right)\right)=G\left(\lambda ,u\right)$ , we obtain that Equation (3.24) is equivalent to

$u=\mu Au+G\left(\lambda ,u\right).$ (3.29)

Obviously, operator $A\mathrm{<mo>\; :\; </mo>}X\to X$ is a linear and compactly continuous map $G\mathrm{<mo>\; :\; </mo>}ℝ\times X\to X$ is compactly continuous.

Next, we show that $G=o\left(\Vert u\Vert \right)$ at $u=0$ uniformly on bounded $\lambda$ intervals. Let

${\xi }_1\left(w\right)=\underset{0\le s\le w}{\max }\left|{\xi }_1\left(s\right)\right|,\mathrm{<mi>\; </mi>}{\xi }_2\left(w\right)=\underset{0\le s\le w}{\max }\left|{\xi }_2\left(s\right)\right|.$ (3.30)

Then ${\xi }_1\mathrm{,\; <mi>\; </mi>}{\xi }_2$ is nondecreasing with respect to $w$ and

$\underset{w\to 0^{+}}{\lim }\frac{{\bar{\xi }}_1\left(w\right)}{w}=0=\underset{w\to 0^{+}}{\lim }\frac{{\bar{\xi }}_2\left(w\right)}{w}.$ (3.31)

Further it follow from (3.31) that

$\frac{\left|{\xi }_2\left(u\right)\right|}{\Vert u\Vert }\le \frac{{\bar{\xi }}_2\left(u\right)}{\Vert u\Vert }\le \frac{{\bar{\xi }}_2\left(\Vert u\Vert \right)}{\Vert u\Vert }\to 0$ (3.32)

as $\Vert u\Vert \to 0$ . Similarly, we have

$\begin{array}{l}\frac{\left|{\xi }_1\left(\lambda l_{0}Tu+{\xi }_2\left(u\right)\right)\right|}{\Vert u\Vert }\\ =\frac{{\bar{\xi }}_1\left(\lambda l_{0}Tu+{\xi }_2\left(u\right)\right)}{\Vert u\Vert }\le \frac{{\bar{\xi }}_1\left(\Vert \lambda l_{0}Tu\Vert +{\bar{\xi }}_2\left(u\right)\right)}{\Vert u\Vert }\\ =\frac{{\bar{\xi }}_1\left(\Vert \lambda l_{0}Tu\Vert +{\bar{\xi }}_2\left(u\right)\right)}{\Vert \lambda l_{0}Tu\Vert +{\bar{\xi }}_2\left(u\right)}\cdot \frac{\Vert \lambda l_{0}Tu\Vert +{\bar{\xi }}_2\left(u\right)}{\Vert u\Vert }\to 0\end{array}$ (3.33)

as $\Vert u\Vert \to 0$ . It concludes our desired result.

Applying the Rabinowitz’s global bifurcation theory [5] [6] to the operator Equation (3.29), we have that there exists a component ${\Sigma }_1$ of $\Sigma$ which contains $\left({\eta }_1^2/l_0^2\mathrm{,0}\right)$ and either is bounded or pass through $\left(\bar{\eta }\mathrm{,0}\right)$ , where $\bar{\eta }$ is another eigenvalue of T. Furthermore, by the Dancer unilateral global bifurcation theory [7] , one gets that there are two distinct unbounded continua, ${\Sigma }_1^{+}$ and ${\Sigma }_1^{-}$ , consisting of the bifurcation branch ${\Sigma }_1$ emanating from $\left({\eta }_1^2/l_0^2\mathrm{,0}\right)$ , which satisfy either ${\Sigma }_1^{+}$ and ${\Sigma }_1^{-}$ are both unbounded or ${\Sigma }_1^{+}\cap {\Sigma }_1^{-}\ne \left({\eta }_1^2/l_0^2\mathrm{,0}\right)$ .

Next, we shall show that

${\Sigma }_1^{+}\subseteq \left(\left\{\left({\eta }_1^2/l_0^2\mathrm{,0}\right)\right\}\cup \left(ℝ\times P^{+}\right)\right)\text{and}{\Sigma }_1^{-}\subseteq \left(\left\{\left({\eta }_1^2/l_0^2\mathrm{,0}\right)\right\}\cup \left(ℝ\times P^{-}\right)\right)\mathrm{.}$

For the case of “+” and “−”, we only prove the “+” case, because of the proof is similar. we accomplish it by contradiction. Assume that there exists $\left({\eta }_{\ast }\mathrm{,}{u}_{\ast }\right)\in {\Sigma }_1^{+}$ , however $\left({\eta }_{\ast }\mathrm{,}{u}_{\ast }\right)\notin \left(\left\{\left({\eta }_1^2/l_0^2\mathrm{,0}\right)\right\}\cup \left(ℝ\times P^{+}\right)\right)$ .

Assertion: For the $\left({\eta }_{\ast }\mathrm{,}{u}_{\ast }\right)\in {\Sigma }_1^{+}$ , we have $\left({\eta }_{\ast }\mathrm{,}{u}_{\ast }\right)\ne \left({\eta }_1^2/l_0^2\mathrm{,0}\right)$ .

Otherwise, by the Dancer’s unilateral global bifurcation theory, then ${\eta }_{\ast }$ must be an eigenvalue of problem (3.29) different to ${\eta }_1^2/l_0^2$ . Hence, there exists a sequence $\left\{\left({\mu }_m\mathrm{,}{u}_m\right)\right\}\subset {\Sigma }_1^{+}$ such that $\left({\mu }_m\mathrm{,}{u}_m\right)\to \left({\eta }_{\ast }\mathrm{,0}\right)$ . Let $w_m=u_m/\Vert u_m\Vert$ . Then one has that

$w_m={\mu }_{m}A{w}_m+\frac{G\left(\lambda ,u_m\right)}{\Vert u_m\Vert }.$ (3.34)

Since $w_m$ is bounded in X, after taking a subsequence if necessary, we have that $w_m\to w_{\ast }$ for some $w_{\ast }\in X$ . It follows from (3.34) and the compactness of $A\mathrm{,\; <mi>\; </mi>}G$ that $w_m\to w_{\ast }$ in X and

$w_{\ast }={\eta }_{\ast }A{w}_{\ast }.$ (3.35)

By Lemma 2.1, $w_{\ast }$ must change its sign. Lemma 2.2 implies the existence of a $c>0$ such that

$\left|\left\{x\in {ℝ}^N\mathrm{<mo>\; :\; </mo>}{w}_{\ast }\left(x\right)\ge 0\right\}\right|\ge c\mathrm{,}$ (3.36)

which is not compatible with the fact of $u_m\le 0$ . So $u_{\ast }\cancel{\equiv }0$ .

It follows from continuity argument that $u_{\ast }$ is a solution of the following problem

$\{\begin{array}{l}-\Delta u={\lambda }_{\ast }\frac{f\left(v_{\ast }\right)}{u_{\ast }}p\left(x\right)u\mathrm{<mi>\; </mi>\; <mi>\; </mi>\; <mi>\; </mi>}x\in {ℝ}^N,\\ u\to \mathrm{0\; <mi>\; </mi>\; <mi>\; </mi>\; <mi>\; </mi>\; <mi>\; </mi>\; <mi>\; </mi>\; <mi>\; </mi>\; <mi>\; </mi>\; <mi>\; </mi>\; <mi>\; </mi>\; <mi>\; </mi>\; <mi>\; </mi>\; <mi>\; </mi>\; <mi>\; </mi>\; <mi>\; </mi>\; <mi>\; </mi>\; <mi>\; </mi>\; <mi>\; </mi>\; <mi>\; </mi>\; <mi>\; </mi>\; <mi>\; </mi>\; <mi>\; </mi>\; <mi>\; </mi>\; <mi>\; </mi>\; <mi>\; </mi>\; <mi>\; </mi>\; <mi>\; </mi>\; <mi>\; </mi>\; <mi>\; </mi>\; <mi>\; </mi>\; <mi>\; </mi>\; <mi>\; </mi>\; <mi>\; </mi>}\text{as}\left|x\right|\to +\infty ,\end{array}$ (3.37)

where $v_{\ast }={\eta }_{\ast }T{u}_{\ast }$ . Clearly, $u_{\ast }\ge 0$ in ${ℝ}^N$ . By strong maximum principle, one has $u_{\ast }>0$ in ${ℝ}^N$ . Thus ${\Sigma }_1^{+}$ and ${\Sigma }_1^{-}$ are both unbounded.

Without loss of generality, we assume that ${\eta }_1^2/l_0^2<{\eta }_1^2/l_{\infty }^2$ . Next, we shall show that ${\Sigma }_1^{\pm }$ joins from $\left({\eta }_1^2/l_0^2\mathrm{,0}\right)$ to $\left({\eta }_1^2/l_{\infty }^2,0\right)$ . We only prove the “+” case. Let $\left\{\left({\mu }_n\mathrm{,}{u}_n\right)\right\}\subset {\Sigma }_1^{+}$ such that ${\mu }_n+\Vert u_n\Vert \to +\infty$ . Clearly, (H1) and (H2) imply that there exist two positive constants $c_1$ and $c_2$ such that

$c_1\le \frac{f\left(s\right)}{s}\le c_2\mathrm{,\; <mi>\; </mi>}{c}_1\le \frac{g\left(s\right)}{s}\le c_2\text{for}\text{any}s\ne 0.$ (3.38)

By Lemma 2.4 and Lemma 2.3, there exist two constant ${\eta }_1^2/c_1^2$ and ${\eta }_1^2/c_2^2$ such that ${\eta }_1^2/c_1^2\le {\mu }_n\le {\eta }_1^2/c_2^2$ . Hence, we obtain that $\Vert u_n\Vert \to +\infty$ as $n\to +\infty$ .

Set $w_n=u_n/{\Vert u\Vert }_n$ . Since $w_n$ is bounded in X, after taking a subsequence if necessary, we have that $w_n\to w$ for some $w\in X$ . Let ${\zeta }_1\mathrm{,\; <mi>\; </mi>}{\zeta }_2\mathrm{<mo>\; :\; </mo>}ℝ\to ℝ$ such that

$f\left(s\right)=l_{\infty }s+{\zeta }_1\left(s\right),\mathrm{<mi>\; </mi>}g\left(s\right)=l_{\infty }s+{\zeta }_2\left(s\right)$ (3.39)

with

$\underset{s\to +\infty }{\lim }\frac{{\zeta }_1\left(s\right)}{s}=0=\underset{s\to +\infty }{\lim }\frac{{\zeta }_2\left(s\right)}{s}.$ (3.40)

Let ${\tilde{\zeta }}_1\left(u\right)={\max }_{0\le s\le u}\left|{\zeta }_1\left(s\right)\right|,\mathrm{<mi>\; </mi>}{\tilde{\zeta }}_2\left(u\right)={\max }_{0\le s\le u}\left|{\zeta }_2\left(s\right)\right|$ , ${\tilde{\zeta }}_1,{\tilde{\zeta }}_2$ are nondecreasing with respect to $u$ .

Define

${\bar{\zeta }}_1\left(u\right)=\underset{\frac{u}{2}\le s\le u}{\max }\left|{\zeta }_1\left(s\right)\right|\mathrm{,\; <mi>\; </mi>}{\bar{\zeta }}_2\left(u\right)=\underset{\frac{u}{2}\le s\le u}{\max }\left|{\zeta }_2\left(s\right)\right|\mathrm{.}$ (3.41)

Then we get that

$\underset{u\to +\infty }{\lim }\frac{{\bar{\zeta }}_1\left(u\right)}{u}=0\text{and}{\tilde{\zeta }}_1\left(u\right)\le {\tilde{\zeta }}_1\left(\frac{u}{2}\right)+{\bar{\zeta }}_1\left(u\right).$ (3.42)

It follow from (3.42) that

$\underset{u\to +\infty }{\lim }\frac{{\tilde{\zeta }}_1\left(u\right)}{u}=0.$ (3.43)

Similarly, we can see that

$\underset{u\to +\infty }{\lim }\frac{{\tilde{\zeta }}_2\left(u\right)}{u}=0.$ (3.44)

It follow from (3.43) and (3.44) that

$\frac{\left|{\zeta }_2\left(u\right)\right|}{\Vert u\Vert }\le \frac{{\tilde{\zeta }}_2\left(u\right)}{\Vert u\Vert }\le \frac{{\tilde{\zeta }}_2\left(\Vert u\Vert \right)}{\Vert u\Vert }\to 0$ (3.45)

as $\Vert u\Vert \to +\infty$ .

Furthermore, it follows that

$\begin{array}{l}\frac{\left|{\zeta }_1\left(\lambda l_{0}Tu+{\xi }_2\left(u\right)\right)\right|}{\Vert u\Vert }\\ =\frac{{\tilde{\zeta }}_1\left(\lambda l_{0}Tu+{\xi }_2\left(u\right)\right)}{\Vert u\Vert }\le \frac{{\tilde{\zeta }}_1\left(\Vert \lambda l_{0}Tu\Vert +{\tilde{\zeta }}_2\left(u\right)\right)}{\Vert u\Vert }\\ =\frac{{\tilde{\zeta }}_1\left(\Vert \lambda l_{0}Tu\Vert +{\tilde{\zeta }}_2\left(u\right)\right)}{\Vert \lambda l_{0}Tu\Vert +{\tilde{\zeta }}_2\left(u\right)}\cdot \frac{\Vert \lambda l_{0}Tu\Vert +{\tilde{\zeta }}_2\left(u\right)}{\Vert u\Vert }\to 0\end{array}$ (3.46)

as $\Vert u\Vert \to +\infty$ . Then by similar argument to the previous processes, we have that

$w={\mu }_{w}Aw,$ (3.47)

where ${\mu }_w={\lim }_{n\to +\infty }{\mu }_n$ . Obviously, $\Vert w\Vert =1,\mathrm{<mi>\; </mi>}w\in \overline{P^{+}}$ . Thus $w\ge 0$ in ${ℝ}^N$ and $w\cancel{\equiv }0$ . It follows from the strong maximum principle (Lemma 2.6) that $w>0$ in ${ℝ}^N$ . By Lemma 2.1, the uniqueness of the principal eigenvalue implies that ${\mu }_w={\eta }_1^2/l_0^2$ . In conclusion, ${\Sigma }_1^{\pm }$ joins from $\left({\eta }_1^2/l_0^2\mathrm{,0}\right)$ to $\left(<{\eta }_1^2/l_{\infty }^2,0\right)$ . By the definition of T, the sign of $u^{+}$ is same as that of $v^{+}$ . Thus there exist two one-sign solutions $\left(u^{+}\mathrm{,}{v}^{+}\right)$ and $\left(u^{-}\mathrm{,}{v}^{-}\right)$ for

$\lambda \in \left(\min \left\{\frac{{\eta }_1}{l_0}\mathrm{,}\frac{{\eta }_1}{l_{\infty }}\right\}\mathrm{,}\max \left\{\frac{{\eta }_1}{l_0}\mathrm{,}\frac{{\eta }_1}{l_{\infty }}\right\}\right)$ .

Proof of Theorem 2.2. Let $\left(u\mathrm{,}v\right)$ is a one-sign solution of problem (1.1) corresponding to $\mu$ . Since $v$ is bounded in ${ℝ}^N$ , without loss of generality, we assume that ${\sup }_{x\in {ℝ}^N}v\left(x\right)\le 1$ .

By the processes of Lemma 3.1, we have

$u\left(x\right)=\mu {\displaystyle {\int }_{{ℝ}^N}}\left|\Gamma \left(x-y\right)\right|p\left(y\right)f\left(v\left(y\right)\right)\text{d}y\mathrm{.}$ (3.48)

Note that (H1) and (H2), we get

$\begin{array}{c}u\left(x\right)=\mu {\displaystyle {\int }_{{ℝ}^N}}\left|\Gamma \left(x-y\right)\right|p\left(y\right)f\left(v\left(y\right)\right)\text{d}y\\ \le \mu c_2{\displaystyle {\int }_{{ℝ}^N}}\left|\Gamma \left(x-y\right)\right|p\left(y\right)v\left(y\right)\text{d}y\mathrm{.}\end{array}$ (3.49)

Let $\pi \left(x\right)=c_2{\displaystyle {\int }_{{ℝ}^N}}\left|\Gamma \left(x-y\right)\right|Q\left(\left|y\right|\right)\text{d}y$ , then we can see

${\left|x\right|}^{N-2}\pi \left(x\right)\le \frac{c_2}{N-2}{\displaystyle {\int }_0^{+\infty }}{\rho }^{N-1}Q\left(\rho \right)\text{d}\rho \mathrm{.}$ (3.50)

It follows from (3.50) that

${\left|x\right|}^{N-2}u\left(x\right)\le \mu c_2\pi \left(x\right)\le \frac{\mu c_6}{N-2}{\displaystyle {\int }_0^{+\infty }}{\rho }^{N-1}Q\left(\rho \right)\text{d}\rho \mathrm{.}$ (3.51)

Since $v\left(x\right)$ is bounded, then one has that

${\displaystyle {\int }_{{ℝ}^N}}p\left(y\right)f\left(v\left(y\right)\right)\text{d}y\le c_2{\displaystyle {\int }_{{ℝ}^N}}Q\left(\left|y\right|\right)\text{d}y\le c_{2}N{\omega }_N{\displaystyle {\int }_0^{+\infty }}{\rho }^{N-1}Q\left(\rho \right)\text{d}\rho .$ (3.52)

Hence, for any $\epsilon >0$ , there exists $d>0$ such that

$\left|{\left|x\right|}^{N-2}{\displaystyle {\int }_{{\Omega }_d}}\left|\Gamma \left(x-y\right)\right|p\left(y\right)f\left(v\left(y\right)\right)\text{d}y\right|<\frac{\epsilon }{4}$ (3.53)

and

$\left|{\displaystyle {\int }_{{\Omega }_d}}p\left(y\right)f\left(v\left(y\right)\right)\text{d}y\right|<4N\left(N-2\right){\omega }_N\epsilon$ (3.54)

for all $x\in {ℝ}^N$ , where ${\Omega }_d=\left\{y\in {ℝ}^N:\left|y\right|\ge d\right\}$ . By Lebesgue dominated convergence theorem, we obtain that

$\underset{\left|x\right|\to +\infty }{\lim }{\left|x\right|}^{N-2}{\displaystyle {\int }_{B_d}}\Gamma \left(x-y\right)p\left(y\right)f\left(v\left(y\right)\right)\text{d}y=N\left(N-2\right){\omega }_N{\displaystyle {\int }_{B_d}}p\left(y\right)f\left(v\left(y\right)\right)\text{d}y\mathrm{,}$ (3.55)

where $B_d=\left\{y\in {ℝ}^N:\left|y\right|\le d\right\}$ . Then we have that

$\begin{array}{l}\left|{\left|x\right|}^{N-2}{\displaystyle {\int }_{{ℝ}^N}}\Gamma \left(x-y\right)p\left(y\right)f\left(v\left(y\right)\right)\text{d}y-\frac{1}{N\left(N-2\right){\omega }_N}{\displaystyle {\int }_{{ℝ}^N}}p\left(y\right)f\left(v\left(y\right)\right)\text{d}y\right|\\ \le \left|{\left|x\right|}^{N-2}{\displaystyle {\int }_{B_d}}\Gamma \left(x-y\right)p\left(y\right)f\left(v\left(y\right)\right)\text{d}y-\frac{1}{N\left(N-2\right){\omega }_N}{\displaystyle {\int }_{B_d}}p\left(y\right)f\left(v\left(y\right)\right)\text{d}y\right|\\ +\left|{\left|x\right|}^{N-2}{\displaystyle {\int }_{{\Omega }_d}}\Gamma \left(x-y\right)p\left(y\right)f\left(v\left(y\right)\right)\text{d}y-\frac{1}{N\left(N-2\right){\omega }_N}{\displaystyle {\int }_{{\Omega }_d}}p\left(y\right)f\left(v\left(y\right)\right)\text{d}y\right|\\ <\left|{\left|x\right|}^{N-2}{\displaystyle {\int }_{B_d}}\Gamma \left(x-y\right)p\left(y\right)f\left(v\left(y\right)\right)\text{d}y-\frac{1}{N\left(N-2\right){\omega }_N}{\displaystyle {\int }_{B_d}}p\left(y\right)f\left(v\left(y\right)\right)\text{d}y\right|+\frac{\epsilon }{2}.\end{array}$ (3.56)

Thus there exists $d_1$ such that

$\left|{\left|x\right|}^{N-2}{\displaystyle {\int }_{B_d}}\Gamma \left(x-y\right)p\left(y\right)f\left(v\left(y\right)\right)\text{d}y-\frac{1}{N\left(N-2\right){\omega }_N}{\displaystyle {\int }_{B_d}}p\left(y\right)f\left(v\left(y\right)\right)\text{d}y\right|<\frac{\epsilon }{2}$ (3.57)

for all $\left|x\right|\ge d_1$ . Therefore, we have

$\left|{\left|x\right|}^{N-2}{\displaystyle {\int }_{{ℝ}^N}}\Gamma \left(x-y\right)p\left(y\right)f\left(v\left(y\right)\right)\text{d}y-\frac{1}{N\left(N-2\right){\omega }_N}{\displaystyle {\int }_{{ℝ}^N}}p\left(y\right)f\left(v\left(y\right)\right)\text{d}y\right|<\epsilon .$ (3.58)

Hence, it follows that

$\underset{\left|x\right|\to +\infty }{\lim }{\left|x\right|}^{N-2}u\left(x\right)=N\left(N-2\right){\omega }_N{\displaystyle {\int }_{{ℝ}^N}}p\left(y\right)f\left(v\left(y\right)\right)\text{d}y.$ (3.59)

Thus there exist constants $c_1,c_2>0$ and $c_3,c_4<0$ such that

$\underset{\left|x\right|\to +\infty }{\lim }{\left|x\right|}^{N-2}{u}^{+}=c_1,\underset{\left|x\right|\to +\infty }{\lim }{\left|x\right|}^{N-2}{v}^{+}=c_2$ (3.60)

and

$\underset{\left|x\right|\to +\infty }{\lim }{\left|x\right|}^{N-2}{u}^{-}=c_3,\underset{\left|x\right|\to +\infty }{\lim }{\left|x\right|}^{N-2}{v}^{-}=c_4.$ (3.61)

4. Conclusion

This article presents the result of an investigation into the existence of positive solution and negative solution on ${ℝ}^N$ . Our results are not only in the given configuration, but also extend single equation to system of equations. For the first question, we apply the Rabinowitz’s global bifurcation theory and the Dancer’s unilateral global bifurcation theory to determine the range of parameter such that the existence of positive solution and negative solution. Under some appropriate assumptions, we also get the decay of positive solution and negative solution by fixing the parameter value on a small interval. We believe that our work is a useful contribution to the existing literature on asymptotically linear systems.

Conflicts of Interest

The author declares no conflicts of interest regarding the publication of this paper.

References

[1]	Edelson, A.L. and Rumbos, A.J. (1993) Linear and Semilinrar Eigenvalue Problem in . Communications in Partial Differential Equations, 18, 215-240. https://doi.org/10.1080/03605309308820928
[2]	Naito, M. (1989) Radial Entire Solutions of the Linear Equation . Hiroshima Mathematical Journal, 19, 431-439. https://doi.org/10.32917/hmj/1206129401
[3]	Dai, G. and Yao, J. (2016) Spectrum and Bifurcation for Semilinear Elliptic Problems in . Journal of Differential Equations, 263, 5939-5967. https://doi.org/10.1016/j.jde.2017.07.004
[4]	Edelson, A.L. (1989) Entire Solutions of Singular Elliptic Equations. Journal of Mathematical Analysis and Applications, 139, 523-532. https://doi.org/10.1016/0022-247X(89)90126-1
[5]	Rabinowitz, P.H. (1973) On Bifurcation from Infinity. Journal of Differential Equations, 14, 462-475. https://doi.org/10.1016/0022-0396(73)90061-2
[6]	Rabinnowitz, P.H. (1971) Some Global Results for Nonlinear Eigenvalue Problems. Journal of Functional Analysis, 7, 487-513. https://doi.org/10.1016/0022-1236(71)90030-9
[7]	Dancer, E.N. (2002) Bifurcation from Simple Eigenvalues of Geometric Multiplicity One. Bulletin of the London Mathematical Society, 34, 533-538. https://doi.org/10.1112/S002460930200108X