Generalization of the Pecaric-Rajic Inequality in a Quasi-Banach Space

Jianbing Cao

Department of Mathematics, Henan Institute of Science and Technology, Xinxiang, China.

DOI: 10.4236/apm.2017.79031                

Abstract

In the present paper, we shall give an extension of the well known Pecaric-Rajic inequality in a quasi-Banach space, we establish the generalized inequality for an arbitrary number of finitely many nonzero elements of a quasi-Banach space, and obtain the corresponding upper and lower bounds. As a result, we get some more general inequalities.

Keywords

Pecaric-Rajic Inequality, Dunkl-Williams Inequality, Triangle Inequality, Quasi-Banach Space

1. Introduction

Let us first recall some basic facts concerning quasi-Banach spaces and some preliminary results. For more information about quasi-Banach spaces, the readers can refer to [1] .

Definition 1 Let be a linear space. A quasi-norm is a real-valued function on satisfying the following:

1. 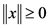for all and 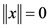if and only if;

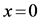2. 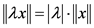for all 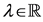and all;

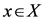3. There is a constant 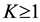such that 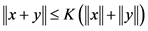for all.

The pair 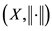is called a quasi-normed space if is a quasi-norm on.

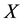A quasi-Banach space is a complete quasi-normed space.

A quasi-norm is called a p-norm if

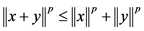
for all. In this case, a quasi-Banach space is called a p-Banach space.

Let be a normed linear space. The following is the well known Dunkl- Williams inequality (see [2] ), which states that the for any two nonzero elements,

(1)

Many authors have studied this inequality over the years, and various refinements of this inequality (1) have been obtained (see e.g [3] [4] [5] ). Pecaric and Rajic [6] got the following inequality in a normed linear space.

(2)

(3)

Furthermore, the authors [6] also showed that these inequalities imply some refinements of the generalized triangle inequalities obtained by some authors. For generalized triangle inequalities, note that, some authors have also got many related results (see [7] [8] ). In this paper, we shall discuss some extensions of the inequalities (2) and (3) for an arbitrary number of finitely many nonzero elements of a quasi-Banach space.

2. Main Results

Note that, given a p-norm, the formula gives us a translation invariant metric on. By the Aoki-Rolewicz theorem [9] (see also [1] ), each quasi-norm is equivalent to some p-norm. Henceforth we can get similar results with p-norm. In the following, we first generalize the inequalities (2) and (3) with p-norm a p-Banach space.

Theorem 2 Let be a p-Banach space and nonzero elements of. Then we have

(4)

(5)

Proof. First, let us prove the inequality (4): for a fixed, we have

from this it follows that

which is the inequality (4). The second inequality (5) follows likewise and the details are omitted.

Now, we generalize the inequalities (2) and (3) with quasi-norm in a quasi- Banach space.

Theorem 3 Let be a quasi-Banach space and nonzero elements of. Then we have

(6)

(7)

where is a constant and.

Proof. First, let us prove the inequality (6): for a fixed, we have

where. Hence, in order to get the inequality (6), let us set

, where for all. Thus, from the above inequality it

follows that

From this it follows that

which is the inequality (6).

In order to proof the second inequality (7), we proceed in a similar way. For a fixed, we get,

where. From this it follows that

where. Hence, in order to proof the inequality (7), let us set

, where for all. Thus, from the above inequality it

follows that

Thus, from the above inequality we can get

This completes the proof.

3. Conclusion

In this paper we establish a generalisation of the so-called Pecaric-Rajic inequality by providing upper and lower bounds for the norm of the linear

combination, where nonzero elements of. Further-

more, we also obtain the corresponding inequalities in a p-Banach space with p- norm. We should also indicate that when in Theorem 3, the inequalities (2) and (3) can be obtained as a particular case of the results established in Theorem 3. Thus, we get some more general inequalities.

Acknowledgements

The author is partly supported by the Science and Technology Research Key Project of Education Department of Henan Province (No. 18A110018).

Conflicts of Interest

The authors declare no conflicts of interest.

References

[1]	Benyamini, Y. and Lindenstrauss, J. (2000) Geometric Nonlinear Functional Analysis. Vol. 1, Volume 48 of American Mathematical Society Colloquium Publications. American Mathematical Society, Providence, 65.
[2]	Dunkl, C.F. and Williams, K.S. (1964) A Simple Norm Inequality. The American Mathematical Monthly, 71, 53-54. https://doi.org/10.2307/2311304
[3]	Maligranda, L. (2006) Simple Norm Inequalities. The American Mathematical Monthly, 113, 256-260. https://doi.org/10.2307/27641893
[4]	Mercer, P.R. (2007) The Dunkl-Williams Inequality in an Inner Product Space. Mathematical Inequalities and Applications, 10, 447-450. https://doi.org/10.7153/mia-10-42
[5]	Pecaric, J. and Rajic, R. (2007) The Dunkl-Williams Equality in Pre-Hilbert C*-Modules. Linear Algebra and its Applications, 425, 16-25. https://doi.org/10.1016/j.laa.2007.03.005
[6]	Pecaric, J. and Rajic, R. (2007) The Dunkl-Williams Inequality with n Elements in Normed Linear Spaces. Mathematical Inequalities and Applications, 10, 461-470. https://doi.org/10.7153/mia-10-44
[7]	Wu, C. and Li, Y. (2008) On the Triangle Inequality in Quasi-Banach Spaces. Journal of Inequalities in Pure and Applied Mathematics, 9, Art. 41, 4.
[8]	Mitrinovic, D.S., Pecaric, J. and Fink, A.M. (2013) Classical and New Inequalities in Analysis (Vol. 61). Springer Science and Business Media.
[9]	Rolewicz, S. (1984) Metric Linear Spaces, PWN-Polish Scientific Publishers, Warsaw, D. Reidel Publ., Dordrecht.