Sharp Upper Bounds for Multiplicative Degree Distance of Graph Operations ()

1. Introduction
A topological index of a graph is a numerical quantity which is structural invariant, i.e. it is fixed under graph automorphism. The simplest topological indices are the number of vertices and edges of a graph. In this paper, we define and study a new topological index called multiplicative degree distance. All graphs considered are simple and connected graphs.
We denote the vertex and the edge set of a graph G by
and
, respectively.
denotes the degree of a vertex v in G. The number of elements in the vertex set of a graph G is called the order of G and is denoted by
. The number of elements in the edge set of a graph G is called the size of G and is denoted by
. A graph with order n and size m edges is called a
-graph. For any
, the distance between u and v in G, denoted by
, is the length of a shortest
-path in G. The edge connective the vertices u and v will be denoted by uv. The complement
of the graph G is the graph with vertex set
, in which two vertices in
are adjacent if and only if they are not adjacent in G.
The join of graphs
and
is denoted by
, and it is the graph with vertex set
and the edge set
The composition of graphs
and
is denoted by
, and it is the graph with vertex set
, and two vertices
and
are adjacent if (
is adjacent to
) or (
and
and
are adjacent). The disjunction of graphs
and
is denoted by
, and it is the graph with vertex set
and
The symmetric di- fference of graphs
and
is denoted by
, and it is the graph with vertex set
and edge set
Let G be a connected graph. The Wiener index
of a graph G is defined as
Dobrynin and Kochetova [1] and Gutman [2] independently proposed a vertex-degree-Weighted version of Wiener index called degree distance or Schultz molecular topological index, which is defined for a connected graph G as
The Zagreb indices have been introduced more than thirth years ago by Gutman and Trianjestic [3] . The first Zagreb index
of a graph G is defined as
The second Zagreb index
of a graph G is defined as
The Zagreb indices are found to have applications in QSPR and QSAR studies as well, see [4] .
Note that contribution of nonadjacent vertex pair should be taken into account when computing the Weighted Wiener Polynomials of certain Composite graphs, see [5] . A.R. Ashrafi, T. Doslic, A. Hamzeha, [6] [7] defined the first Zagreb coindex of a graph G is
The second Zagreb coindex of a graph G is
respectively.
In [8] , Hamzeh, Iranmanesh Hossein-Zadeh and M.V. Diudea recently introduced the generalized degree distance of graphs. Asma Hamzeh, Ali Iranmanesh and Samaneh Hossein-Zadeh, Cartesian product, composition, join, disjunction and symmetric difference of graphs and introduce generalized and modified generalized degree distance Polynomials of graphs, such that their first derivatives at
, see [9] .
In this paper, we defne a new graph invariant named multiplicative version of degree distance of a graph denoted by
and defined by
Therefore the study of this new topological index is important and we have obtained Sharp upper bounds for the graph operations such as join, disjunction, composition, symmetric difference of graphs.
2. The Multiplicative Degree Distance of Graph Operations
Lemma 2.1. [10] [11] , Let
and
be two simple connected graphs. The number of vertices and edges of graph
is denoted by
and
respectively for
. Then we have
1.
For a vertex u of
,
and for a vertex v of
,
2.
3.
4.
Lemma 2.2. (Arithmetic Geometric inequality)
Let
be non-negative numbers. Then
Remark 2.3. For a graph G, let
= {
and
are adjacent in
} and let
= {
and
are not adjacent in
}. For each
. Clearly,
Let
and
Clearly
,
.
The summation
runs over the ordered pairs of
. For simplicity, we write the summation
as
. Similarly, we write the summation
as
. Also the summation
runs over the edges of G. We denote the summation
by
and similarly
by
. The summation
eqivalent to
and similarly the summation
eqivalent to
.
Lemma 2.4. Let G be a graph. Then
Proof:
Lemma 2.5.
Proof: Let
and
. Let
be the neighbours of x. Each orderd pair
contributes
to the sum. Thus these orderd pairs contribute
to the sum. Hence
Lemma 2.6.
Proof: Clearly,
Lemma 2.7.
Proof:
Lemma 2.8.
Proof.
Lemma 2.9.
Proof:
Lemma 2.10.
Proof:
3. The Multiplicative Degree Distance of Composition of Graph
Theorem 3.1. Let
, be a
-graph. Then
Proof:
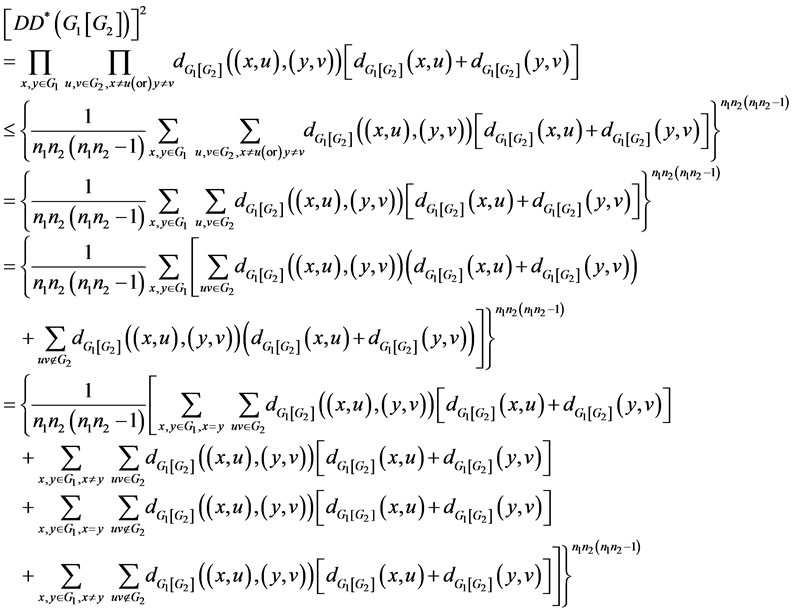
where
are terms of the above sums taken in order.
Next we calculate
and
separately.
Lemma 3.2.
Proof: Clearly the graph
is the complete graph
.
(1)
Remark 3.3. Let
and
. We get,
In Theorem 3.1, put
and
, we get
(2)
From (1) and (2) our bound is tight
4. The Multiplicative Degree Distance of Join of Graph
Theorem 4.1. Let
, be a
-graph and let
. Then
Proof:

where
are terms of the above sums taken in order.
Next we calculate
and
separately one by one. Now,
Lemma 4.2.
Proof: Clearly the graph
is the complete graph
(3)
Remark 4.3. Let
and
. We get,
In Theorem 4.1, put
we get
(4)
From (3) and (4) our bound is tight.
5. The Multiplicative Degree Distance of Disjunction of Graph
Theorem 5.1. Let
, be a
-graph and let
. Then
Proof:
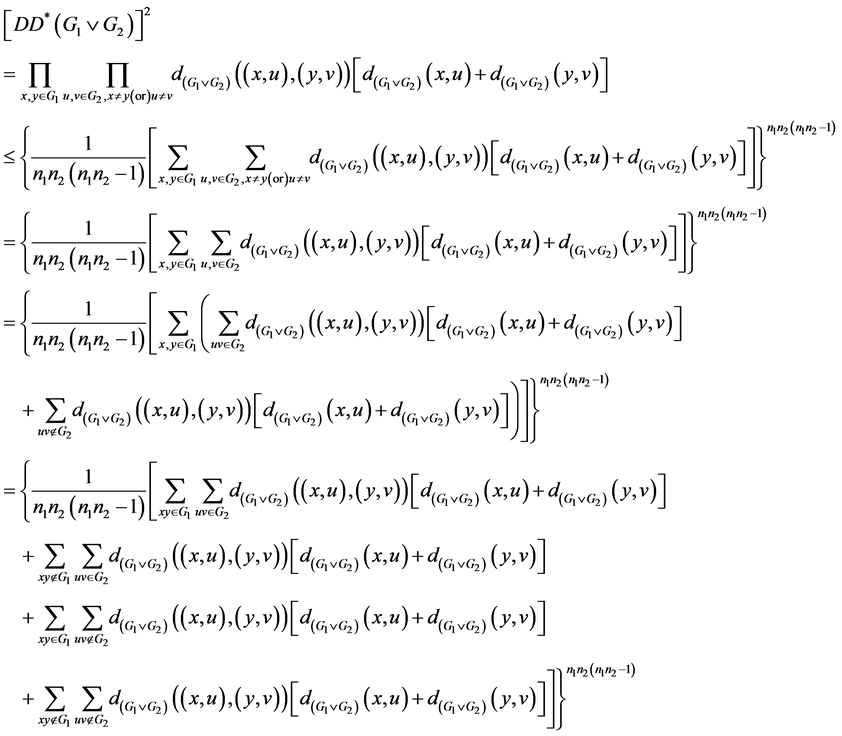
where
are terms of the above sums taken in order.
Next we calculate
and
separately one by one. Now,
where
and
are terms of the above sums taken in order.
Now,
Lemma 5.2.
Proof: Clearly the graph
is the complete graph
.
(5)
Remark 5.3. Let
and
. We get
In Theorem 5.1, put
and
, we get
(6)
From (5) and (6) our bound is tight.
6. The Multiplicative Degree Distance of Symmetric difference of Graph
Theorem 6.1.
Proof:
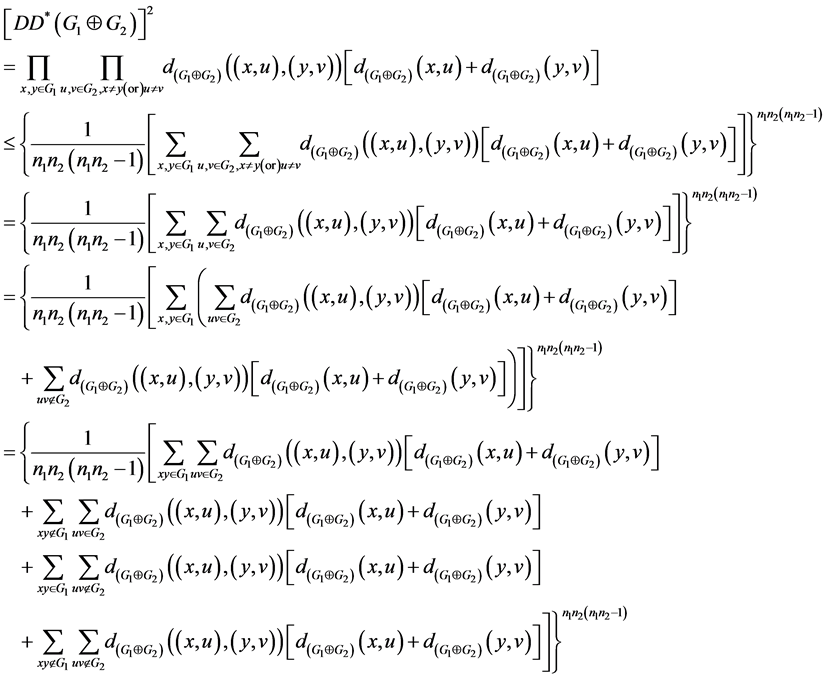
where
are terms of the above sums taken in order.
Next we calculate
and
separately.
where
and
denote the sums of the above terms in order.
Now,
Lemma 6.2.
Proof: Clearly the graph
is the complete graph
(7)
Remark 6.3. Let
and
. We get
In Theorem 6.1, put
and
, we get
(8)
From (7) and (8) our bound is tight.