An Application of Generalized Entropy Optimization Methods in Survival Data Analysis

Aladdin Shamilov¹, Cigdem Kalathilparmbil^1*, Sevda Ozdemir²

¹Faculty of Science, Department of Statistics, Anadolu University, Eskişehir, Turkey.
²Ozalp Vocational School, Accountancy and Tax Department, Yuzuncu Yil University, Van, Turkey.

DOI: 10.4236/jmp.2017.83024                

Abstract

In this paper, survival data analysis is realized by applying Generalized Entropy Optimization Methods (GEOM). It is known that all statistical distributions can be obtained as distribution by choosing corresponding moment functions. However, Generalized Entropy Optimization Distributions (GEOD) in the form of distributions which are obtained on basis of Shannon measure and supplementary optimization with respect to characterizing moment functions, more exactly represent the given statistical data. For this reason, survival data analysis by GEOD acquires a new significance. In this research, the data of the life table for engine failure data (1980) is examined. The performances of GEOD are established by Chi-Square criteria, Root Mean Square Error (RMSE) criteria and Shannon entropy measure, Kullback-Leibler measure. Comparison of GEOD with each other in the different senses shows that along of these distributions (MinMaxEnt)₄ is better in the senses of Shannon measure and of Kullback-Leibler measure. It is showed that, (MinMaxEnt)₃ ((MaxMaxEnt)₄) is more suitable for statistical data among (MinMaxEnt)_m,m=1,2,3,4(MaxMaxEnt)_m,m=1,2,3,4. Moreover, (MinMaxEnt)₃ is better for statistical data than (MaxMaxEnt)₄ in the sense of RMSE criteria. According to obtained distribution (MinMaxEnt)₃ (MaxMaxEnt)₄ estimator of Probability Density Function f^{^} (t), Cumulative Distribution Functio F^{^} (t) , Survival Function Ŝ(t) and Hazard Rate ĥ(t) are evaluated and graphically illustrated. The results are acquired by using statistical software MATLAB.

Keywords

Survival Function, Censored Observation, Generalized Entropy Optimization Methods, Distributions

1. Introduction

Entropy Optimization Methods (EOM) have important applications, especially in statistics, economy, engineering and so on. There are several examples in the literature that known statistical distributions do not conform to statistical data; however, the entropy optimization distributions conform well. Generalized Entropy Optimization Methods (GEOM) have suggested distributions in the form of MinMaxEnt which is the closest to statistical data, and MaxMaxEnt which is the furthest from mentioned data in the sense of information theory [1] [2] , respectively. For this reason, GEOM can be more successfully applied in Survival Data Analysis.

Different aspects and methods of investigations of survival data analysis are considered in [3] - [8] .

In particular in the paper [6] , it is investigated several problems of hazard rate function estimation based on the maximum entropy principle. The potential applications include developing several classes of the maximum entropy distributions which can be used to model different data-generating distributions that satisfy certain information constraints on the hazard rate function.

In order to represent the results of our investigations, we give some auxiliary concepts and facts first.

2. Survival Analysis

Survival time can be defined broadly as the time to the occurrence of a given event. This event can be the development of a disease, response to a treatment, relapse or death [9] .

Censoring: The techniques for reducing experimental time are known as censoring. In survival analysis, the observations are lifetimes, which can be indefinitely long. So quite often the experiment is so designed that the time required for collecting the data is reduced to manageable levels.

Let 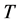be a continuous, non-negative valued random variable representing the lifetime of a unit. This is the time for which an individual (or unit) carries out its appointed task satisfactorily and then passes into “failed’’ or “dead’’ state thereafter [10] .

The probabilistic properties of the random variable are studied through its cumulative distribution function 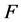or other equivalent functions defined below [9] :

Cumulative Distribution Function:

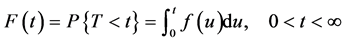
Survival Function: This function is denoted by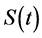, is defined as the probability that an individual survives longer than:

Probability Density Function: Like any other continuous random variable, the survival time has a probability density function defined as the limit of the probability that an individual fails in the short interval per unit width, or simply the probability of failure in a small interval per unit time. It can be expressed as

Hazard Rate: This function is defined as the probability of failure during a very small time interval, assuming that the individual has survived to the beginning of the interval, or as the limit of the probability that an individual fails in a very short interval, , given that the individual has survived to time:

3. Generalized Entropy Optimization Methods (GEOM)

Entropy Optimization Problem (EOP) [11] and Generalized Entropy Optimization problem (GEOP) [10] can be formulated in the following form.

EOP: Let be given probability density function (p.d.f.) of random variable, be an entropy optimization measure and be a given moment vector function generating moment constraints. It is required to obtain the distribution corresponding to, which gives extreme value to.

GEOP: Let be given probability density function of random variable, be an entropy optimization measure and be a set of given moment vector functions. It is required to choose moment vector functions, such that defines entropy optimization distribution closest to, defines entropy optimization distribution furthest from with respect to entropy optimization measure. If is taken as Shannon entropy measure, then is called the distri- bution, and is called the distribution [1] [2] [12] [13] [14] .

The method of solving GEOP is called as GEOM.

3.1. Functional

The problem of maximizing entropy function

(1)

subject to constraints

(2)

where

has solution

(3)

where are Lagrange multipliers. Finding the distribution which maximizes function (1) subject to constraints generated by equations in (2) is an optimization problem. In the literature, there have been numerous studies that have calculated these multipliers [1] . In this study, we use the MATLAB program to calculate Lagrange multipliers.

If (3) is substituted into (1), the maximum entropy value is obtained:

(4)

If distribution is calculated from the data, the moment vector value can be obtained for each moment vector function. Thus, is considered as a functional of and called the functional. Therefore, we use the notation to denote the maximum value of corresponding to

.

3.2. and Distributions

Let be the compact set of moment vector functions reaches its least and greatest values in this compact set, because of its continuity property. For this reason,

Consequently,

Distributions and corresponding to the and, respectively, are called and

distributions [1] .

method for a finite set of characterizing moment functions can be defined in following form.

Let be the set of characterizing moment vector functions and all combinations of elements of taken elements at a time be. We note that, each element of is vector with components.

Solving the and the problems require to find vector functions, , where

minimizing and maximizing accordingly with respect to Shannon entropy measure. It should be noted that reaches its minimum value subject to constraints generated by function and all -dimensional vector functions. In other words, minimum value of is least value of values corresponding to

. If gives the minimum value to then distribution corresponding to is called the

distribution. method represents probability distribution in the form of distribution. In a similar way, reaches its maximum value subject to constraints generated by function and all -dimensional vector functions. In other words, maximum value of is greatest value of values corresponding to

. If gives the maximum value to then distribution corresponding to is called the

distribution. method represents probability distribution in the form of distribution. It should be noted that both distributions can be applied in solving proper problems in survival data analysis.

4. Application of and Methods to Survival Data

4.1. and Distributions for Finite Set of Characterizing Moment Functions

In the present research, the data of the life table for engine failure data (1980) given in Table 1 is considered [10] .

In our investigation, the experiment is planned for 200 numbers of patients surviving at beginning of interval but the presence of censoring from the planning patients 97 individuals stay out the experiment. This situation is taken into account in Table 2.

It should be noted that, the presence of censoring in the survival times leads to a situation where the sum of observation probabilities stands less than 1 for the

Table 1. The data of the life table for engine failure data (1980).

Table 2. Observed and corrected probabilities.

survival data. For this reason, in solving many problems, it is required to supplement the sum of observation probabilities up to 1. Since the sum of observed probabilities in Table 2 is 0.8155, according to the number of censoring, supplementary probability is uniformly distributed to each censoring data and corrected probabilities are obtained.

As we noted that above, and distributions can be applied in solving proper problems in survival data analysis. In our investigation as components of characterizing moment vector function

, are chosen. The set of moment functions is chosen from the characteristic moments which are mostly used in Statistics.

Consequently,. For example, if then

gives the least value to and

gives the greatest value to.

The distributions corresponding to

and values are shown in Tables 3-6. In these tables, and distributions corresponding to and are represented with bold font. By virtue of these tables are also obtained, ,

distributions which are shown in Table 7 and Table 8.

In order to obtain the performance of the mentioned distributions, we use various criteria as Root Mean Square Error (RMSE), Chi-Square, entropy values of distributions. The acquired results are demonstrated in Table 9 and Table 10.

All distributions are acceptable to survival data in the sense of Chi ? Square criteria.

In the sense of RMSE criteria each distribution is better than corresponding distribution. Moreover, is nearer to statistical data than and

Table 3. The predicted probabilities for the distribution corresponding to

Table 4. The predicted probabilities for the distribution corresponding to

Table 5. The predicted probabilities for the distribution corresponding to

Table 6. The predicted probabilities for the distribution corresponding to

Table 7. Distributions of.

Table 8. Distributions of.

distributions; each is better than all of distributions. From these results follows that among of distributions, the distribution is more suitable and among of distributions, the distribution is more convenient for statistical data. These results are also corroborated by graphical representation (see Figures 1-4). Consequently, we shall consider Probability Density Function, Cumulative Distribution Function, Survival Function and Hazard Rate for only and distributions.

Although the distribution with the largest number of moment functions tends to fit better, it should be noted that in some cases, the set of moment functions with fewer elements is more informative then a different set of moment functions with more number of elements.

Table 9. The obtained results for,.

Table 10. The obtained results for,.

(a) (b)

Figure 1. Graphic of and distributions.

(a) (b)

Figure 2. Graphic of and distributions.

(a) (b)

Figure 3. Graphic of and distributions.

(a) (b)

Figure 4. Graph of and distributions.

4.2. Availability of GEOD to Survival Data in the Sense of Shannon Measure

In order to establish availability of GEOD to survival data in the sense of Shannon measure it is required to consider entropy values of GEOD.

From Table 3 it is seen that the (the) distribution is realized by vector function and

.

From Table 4 it is seen that the (the) distribution is realized by vector function

and

.

From Table 5 it is seen that the (the) distribution is realized by vector function

and

.

From Table 6 it is seen that the (the) distribution is realized by vector function

and.

Comparison of GEOD with each other in the sense of Shannon measure shows that along of these distributions is better.

The results of our investigation according to using known characterizing moment vector functions from are summarised in the form of following Corollary.

Corollary 1. If by denote the

(the) distribution corresponding to moment conditions generated by moment functions, then inequality

is fulfilled, when. In other words, entropy value of the (the) distribution depending on the number of moment conditions decreases.

Moreover for any the inequality

takes place.

4.3. Availability of GEOD to Survival Data in the Sense of Kullback-Leibler Measure

Now, we calculate the distance between observed distribution

given in Table 2 and distributions

given in Table 7 and Table 8 respectively.

It is known that the Kullback ? Leibler distance between distributions

and is obtained by formula

.

By starting these formula Kullback-Leibler measures for the distance between observed distribution and distributions

are given in Table 11 and Table 12 respectively.

From Table 11 and Table 12 follows that along of GEOD is better in the sense of Kullback-Leibler measure.

The results of our investigation according to using known characterizing moment vector functions from are summarised in the form of following Corollary.

Corollary 2. If observed distribution and

denote the (the) distribution corresponding to moment conditions generated by moment functions, then inequality

is fulfilled, when. In other words, Kullback-Leibler value of the (the) distribution depending on the number of moment conditions decreases.

Moreover for any the inequality

takes place.

Table 11. Kullback-Leibler measure of distributions.

Table 12. Kullback-Leibler measure of distributions.

4.4. Survival Expression of Distributions,

In this section survival data analysis is conducted by

distribution since the above acquired investigations is more presentable for survival data among, distributions.

and estimations of Probability Density Function, Cumulative Distribution Function, Survival Function and Hazard Rate are given in Table 13 & Table 14, respectively.

On basis of the results given in Table 13 & Table 14, graphs of, and are demonstrated in Figures 5(a)-(c) & Figures 6(a)-(c).

Table 13. Survival analysis by.

Table 14. Survival analysis by.

(a) (b)(c)

Figure 5. Survival expression of distribution.

5. Conclusion

In this study, it is established that survival data analysis is realized by applying Generalized Entropy Optimization Methods (GEOM). Generalized Entropy Optimization Distributions (GEOD) in the form of, distributions which are obtained on basis of Shannon measure and supplementary optimization with respect to characterizing moment functions, more exactly represent the given statistical data. For this reason, survival data analysis by GEOD acquires a new significance. The performances of GEOD are established by Chi-Square criteria, Root Mean Square Error (RMSE) criteria and Shannon entropy measure, Kullback-Leibler measure. Comparison of GEOD with each other in the different senses shows that along of these distributions is better in the senses of Shannon measure and of Kullback-Leibler measure. It

(a) (b)(c)

Figure 6. Survival expression of distribution.

is showed that, is more suitable for statistical data among. Moreover, is better for statistical data than in the sense of RMSE criteria. According to obtained distribution

estimator of Probability Density Function, Cumulative Distribution Function, Survival Function and Hazard Rate are evaluated and graphically illustrated. These results are also corroborated by graphical representation. Our investigation indicates that GEOM in survival data analysis yields reasonable results.

Conflicts of Interest

The authors declare no conflicts of interest.

References

[1]	Shamilov, A. (2006) A Development of Entropy Optimization Methods. Wseas Transactions on Mathematics, 5, 568-575.
[2]	Shamilov, A. (2007) Generalized Entropy Optimization Problems and the Existence of Their Solutions. Physica A: Statistical Mechanics and Its Applications, 382, 465-472. https://doi.org/10.1016/j.physa.2007.04.014
[3]	Kaminski, D. and Geisler, C. (2012) Survival Analysis of Faculty Retention in Science and Engineering by Gender. Science, 335, 864-866. https://doi.org/10.1126/science.1214844
[4]	Reingold, E.M., Reichle, E.D. and Glaholt, M.G. (2012) Heather Sheridan, Direct Lexical Control of Eye Movements in Reading: Evidence from a Survival Analysis of Fixation Durations. Cognitive Psychology, 65, 177-206.
[5]	Wang, H. and Dai, H.S. (2012) Accelerated Failure Time Models for Censored Survival Data under Referral Bias. Biostatistics, 14, 313-326.
[6]	Ebrahimi, N. (2000) The Maximum Entropy Method for Lifetime Distributions. Sankhya: The Indian Journal of Statistics, Series A, 62, 236-243.
[7]	Guyot, P., Ades, A., Ouwens, M.J. and Welton, N.J. (2012) Enhanced Secondary Analysis of Survival Data: Reconstructing the Data from Published Kaplan-Meier Survival Curves. BMC Medical Research Methodology, 12, 9. https://doi.org/10.1186/1471-2288-12-9
[8]	Joly, P., Gerds, T.A., Qvist, V., Commenges, D. and Keiding, N. (2012) Estimating Survival of Dental Fillings on the Basis of Interval-Censored Data and Multi-State Models. Statistics in Medicine, 31, 11-12.
[9]	Lee, E.T. and Wang, J.W. (2003) Statistical Methods for Survival Data Analysis. Wiley-Interscience, Oklahoma.
[10]	Deshpande, J.V. and Purohit, S.G. (2005) Life Time Data: Statistical Models and Methods, Series on Quality. Vol. 11, Reliability and Engineering Statistics, India.
[11]	Kapur, J.N. (1992) Kesavan, Entropy Optimization Principles with Applications.
[12]	Shamilov, A. (2009) Entropy, Information and Entropy Optimization. T.C. Anadolu University Publication, Eskisehir.
[13]	Shamilov, A. (2010) Generalized Entropy Optimization Problems with Finite Moment Functions Sets. Journal of Statistics and Management Systems, 13, 595-603. https://doi.org/10.1080/09720510.2010.10701489
[14]	Shamilov, A., Giriftinoglu, C., Usta, I. and Mert Kantar, Y. (2008) A New Concept of Relative Suitability of Moment Function Sets. Applied Mathematics and Computation, 206, 521-529. https://doi.org/10.1016/j.amc.2008.05.063